Journal of Applied Mathematics and Physics
Vol.2 No.2(2014), Article ID:42095,8 pages DOI:10.4236/jamp.2014.22002
Determination of an Unknown Source in the Heat Equation by the Method of Tikhonov Regularization in Hilbert Scales
1College of Science, Guangdong Ocean University, Zhanjiang, China
2School of Mathematics and Statistics, Zhejiang University of Finance and Economics, Hangzhou, China
Email: dongdongzb@gmail.com
Received December 9, 2013; revised January 9, 2014; accepted January 15, 2014
ABSTRACT
In this paper, we consider the problem for determining an unknown source in the heat equation. The Tikhonov regularization method in Hilbert scales is presented to deal with ill-posedness of the problem and error estimates are obtained with a posteriori choice rule to find the regularization parameter. The smoothness parameter and the a priori bound of exact solution are not needed for the choice rule. Numerical tests show that the proposed method is effective and stable.
Keywords:Ill-Posed Problem; Unknown Source; Heat Equation; Regularization Method; Discrepancy Principle in Hilbert Scales
1. Introduction
In this paper, we consider the following problem for determining the unknown source in the heat equation [1]:
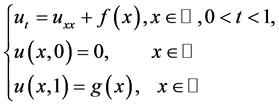 (1.1)
(1.1)
where 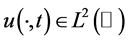 represents state variable. Our purpose is to identify the source term
represents state variable. Our purpose is to identify the source term  from the data
from the data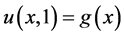 . This problem is called the inverse source problem. In practice, the data at
. This problem is called the inverse source problem. In practice, the data at 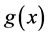 are often obtained on the basis of reading of physical instrument. So only the perturbed data
are often obtained on the basis of reading of physical instrument. So only the perturbed data 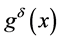 can be obtained. We assume that the exact and measured data satisfy
can be obtained. We assume that the exact and measured data satisfy
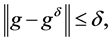 (1.2)
(1.2)
where 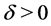 denotes the noisy level,
denotes the noisy level, 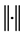 denotes the
denotes the 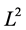 -norm.
-norm.
A variety of important problems in science and engineering involve the inverse source problems, e.g. heat conduction, crack identification electromagnetic theory, geophysical prospecting and pollutant detection. These problems are well known to be ill posed (the solution, if it exists, does not depend continuously on the data). Thus, the numerical simulation is very difficult and some special regularization is required. A few papers have presented the mathematical analysis and effective algorithms of these problems. The uniqueness and conditional stability results for these problems can be found in [2-7]. Some numerical reconstruction schemes can be found in [1,8-17].
In [1], the optimal error bound of the problem (1.1) has been obtained and a Fourier regularization method with an a prior parameter choice rule has been presented. It is well known that the ill posed problem is usually sensitive to the regularization parameter and the a priori bound is difficult to be obtained precisely in practice. In [18], we have used a modified Tikhonov regularization method with an a posteriori choice to solve the problem. But the smoothness parameter (which is usually unknown) is needed for that method. In this paper, we will use the method of Tikhonov regularization in Hilbert scales to solve the problem. We will show that the regularization parameter can be chosen by a discrepancy principle in Hilbert scales which is proposed by Neubauer [19]. The smoothness parameter and the a priori bound of exact solution are not needed for the new method.
This paper is organized as follows. In Section 2, we will give the method of Tikhonov regularization in Hilbert scales for the problem (1.1). The choice of regularization parameter and corresponding convergence results will be found in Section 3. Some numerical results are given in Section 4 to show the effectiveness of the new method.
2. The Method of Tikhonov Regularization in Hilbert Scales for the Problem (1.1)
Let  denote the Fourier transform of
denote the Fourier transform of  defined by
defined by
 (1.3)
(1.3)
and 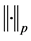 denotes the norm in Sobolev space
denotes the norm in Sobolev space 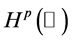 defined by
defined by
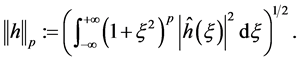 (1.4)
(1.4)
When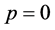 ,
,  denotes the
denotes the 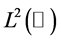 norm.
norm.
Application of the Fourier transform technique to problem (1.1) with respect to the variable ![]() yields the following problem in the frequency space:
yields the following problem in the frequency space:
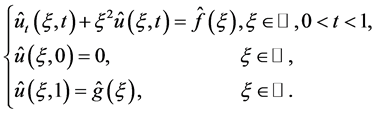 (1.5)
(1.5)
It is easy to see that the solution of problem (1.5) is
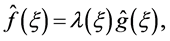 (1.6)
(1.6)
where
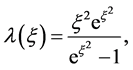 (1.7)
(1.7)
or equivalently, the solution of problem (1.1) is given by
 (1.8)
(1.8)
It is apparent that the exact data ![]() must decay faster than the rate
must decay faster than the rate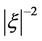 . However, in general, the measured data
. However, in general, the measured data  does not possess such a decay property. In the following, we apply the Tikhonov regularization method to reconstruct a new function
does not possess such a decay property. In the following, we apply the Tikhonov regularization method to reconstruct a new function 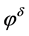 from the perturbed data
from the perturbed data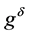 .
. 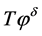 will give a reliable approximation of
will give a reliable approximation of![]() . Before doing that, we impose an a priori bound on the unknown source
. Before doing that, we impose an a priori bound on the unknown source
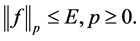 (1.9)
(1.9)
In this case, we let 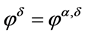 be the minimizer of the Tikhonov functional
be the minimizer of the Tikhonov functional
 (1.10)
(1.10)
where 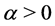 is a regularization parameter and
is a regularization parameter and  is a positive real number. It can be verified that
is a positive real number. It can be verified that 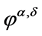 is the solution of the following equation [20]
is the solution of the following equation [20]
 (1.11)
(1.11)
So we can get
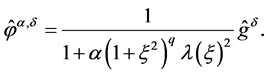 (1.12)
(1.12)
That is to say
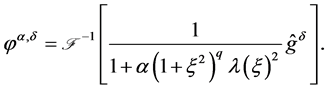 (1.13)
(1.13)
By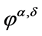 , we can give an approximation of
, we can give an approximation of ![]() as follows:
as follows:
 (1.14)
(1.14)
Lemma 1 For any , we have
, we have
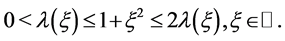 (1.15)
(1.15)
Lemma 2 [21] For![]() , we have
, we have
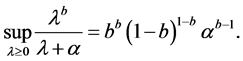 (1.16)
(1.16)
Lemma 3
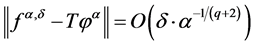 (1.17)
(1.17)
where 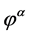 is the unique minimizer of (1.10) with
is the unique minimizer of (1.10) with ![]() instead of
instead of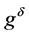 .
.
Proof 1 Due to Parseval formula and Lemma 1
 (1.18)
(1.18)
The proposition follows by applying (1.16) with ![]() replaced by
replaced by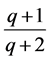 .
.
Lemma 4
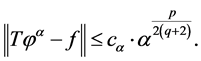 (1.19)
(1.19)
where  is defined by
is defined by
 (1.20)
(1.20)
Proof 2 With the representation
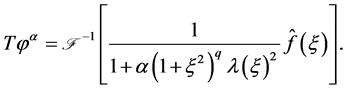 (1.21)
(1.21)
and Lemma 1, we have
 (1.22)
(1.22)
3. The Choice of Regularization Parameter α and Convergence Results
For any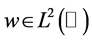 , we define
, we define
 (1.23)
(1.23)
It is apparent that the function 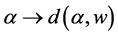 is continuous and strictly increasing on
is continuous and strictly increasing on 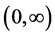 and
and
 (1.24)
(1.24)
So we can get the following lemma.
Lemma 5 Let![]() ,
, 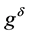 and
and 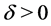 satisfy (1.2) and
satisfy (1.2) and
 (1.25)
(1.25)
for some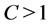 . Then there is a unique
. Then there is a unique  such that
such that
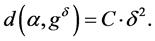 (1.26)
(1.26)
In the following, we denote the unique ![]() determined in (1.26) by
determined in (1.26) by![]() . In the next lemma we consider the behavior of
. In the next lemma we consider the behavior of![]() .
.
Lemma 6 Let![]() ,
,  and
and  satisfy (1.2) and (1.25) for a
satisfy (1.2) and (1.25) for a , then 1)
, then 1)
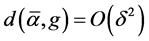 (1.27)
(1.27)
2)
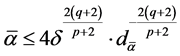 (1.28)
(1.28)
where
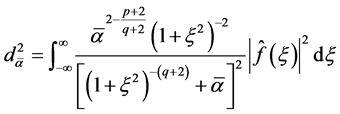 (1.29)
(1.29)
Proof 1) Let
 (1.30)
(1.30)
then
 (1.31)
(1.31)
2)
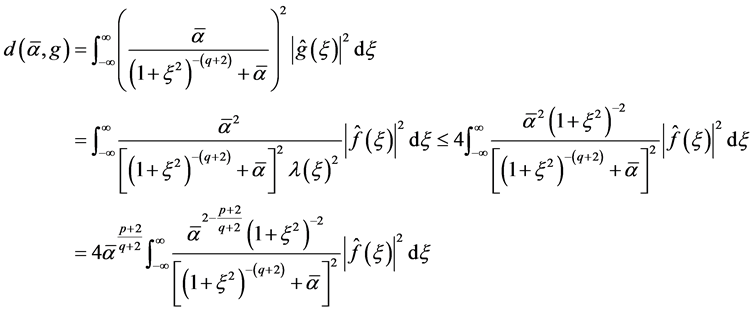 (1.32)
(1.32)
The rest follows from 1).
Now we can prove the main result of this paper.
Theorem 1 Let![]() ,
,  and
and 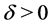 satisfy (1.2) and (1.25) for a
satisfy (1.2) and (1.25) for a ,
, .
. 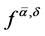 is defined by (1.14) with the regularization parameter
is defined by (1.14) with the regularization parameter ![]() chosen in (1.26), then
chosen in (1.26), then
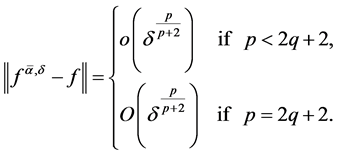 (1.33)
(1.33)
Proof 4 With Lemma 3, Lemma 4, Lemma 6, we obtain
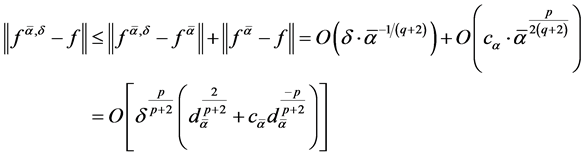 (1.34)
(1.34)
Using the Hölder inequality, (1.20) and (1.29) we get
 (1.35)
(1.35)
Combining (1.34) and (1.35), we obtain
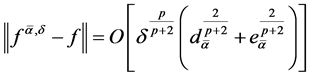 (1.36)
(1.36)
where  is defined by
is defined by
 (1.37)
(1.37)
Since  for
for 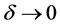 and
and
 (1.38)
(1.38)
The theorem is proved.
4. Numerical Examples
The proposed method can be easily implemented numerically by the fast Fourier transform. We consider the following example.
Example[1] It is easy to verify that the pair of functions
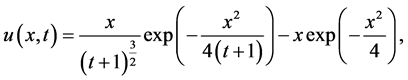 (1.39)
(1.39)
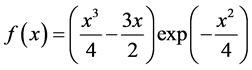 (1.40)
(1.40)
is the exact solution of problem (1.1) with data
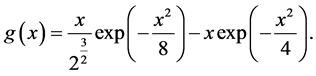 (1.41)
(1.41)
Since 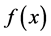 approaches zero as
approaches zero as , we always fix the interval
, we always fix the interval  in the numerical experiment. Let
in the numerical experiment. Let . The perturbed data are given by
. The perturbed data are given by
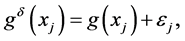 (1.42)
(1.42)
where  are generated by Function
are generated by Function 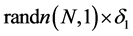 in Matlab.
in Matlab.
In the following, we present numerical results to check the efficiency of the method. In the following, we present numerical results of some examples to check the efficiency of the method and we will also compare the method (M1) with the method in [18] (M2, notate the approximate function as ).
).
It is obvious that the condition (1.9) holds for any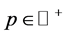 . So we have
. So we have 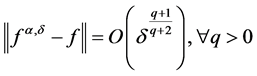 for M1 and
for M1 and 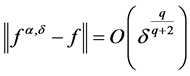 for M2. The relative error has been displayed in Table 1, we can see that when
for M2. The relative error has been displayed in Table 1, we can see that when
![]() decreases from
decreases from  to
to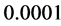 , the errors
, the errors 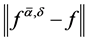 become smaller and the results of M1 are better than M2.
become smaller and the results of M1 are better than M2.
5. Conclusion
In this paper, we present a modified Tikhonov regularization method for identifying an unknown source in the heat equation and the theoretical results show that the method is Order optimal. The numerical example also verified the efficiency and accuracy of the method.
Table 1. Numerical results with a posteriori parameter.
Acknowledgements
The project is supported by the National Natural Science Foundation of China (No.11201085).
REFERENCES
- F. F. Dou, C. L. Fu and F. L. Yang, “Optimal Error Bound and Fourier Regularization for Identifying an Unknown Source in the Heat Equation,” Journal of Computational and Applied Mathematics, Vol. 230, No. 2, 2009, pp. 728-737. http://dx.doi.org/10.1016/j.cam.2009.01.008
- J. R. Cannon and P. Du Chateau, “Structural Identification of an Unknown Source term in a Heat Equation,” Inverse Problems, Vol. 14, No. 3, 1998, pp. 535-551. http://dx.doi.org/10.1088/0266-5611/14/3/010
- J. R. Cannon and S. Perez-Esteva, “Uniqueness and Stability of 3d Heat Sources,” Inverse Problems, Vol. 7, No. 1, 1991, pp. 57-62. http://dx.doi.org/10.1088/0266-5611/7/1/006
- M. Choulli and M. Yamamoto, “Conditional Stability in Determining a Heat Source,” Journal of Inverse and Ill-Posed Problems, Vol. 12, No. 3, 2004, pp. 233-243. http://dx.doi.org/10.1515/1569394042215856
- A. El Badia and T. Ha-Duong, “On an Inverse Source Problem for the Heat Equation. Application to a Pollution Detection Problem,” Journal of Inverse and Ill-Posed Problems, Vol. 10, No. 6, 2002, pp. 585-600. http://dx.doi.org/10.1515/jiip.2002.10.6.585
- G. S. Li, “Data Compatibility and Conditional Stability for an Inverse Source Problem in the Heat Equation,” Applied Mathematics and Computation, Vol. 173, No. 1, 2006, pp. 566-581. http://dx.doi.org/10.1016/j.amc.2005.04.053
- M. Yamamoto, “Conditional Stability in Determination of Force Terms of Heat Equations in a Rectangle,” Mathematical and Computer Modelling, Vol. 18, No. 1, 1993, pp. 79-88. http://dx.doi.org/10.1016/0895-7177(93)90081-9
- A. A. Burykin and A. M. Denisov, “Determination of the Unknown Sources in the Heat-Conduction Equation,” Computational Mathematics and Modeling, Vol. 8, No. 4, 1997, pp. 309-313. http://dx.doi.org/10.1016/0895-7177(93)90081-9
- A. Farcas and D. Lesnic, “The Boundary-Element Method for the Determination of a Heat Source Dependent on One Variable,” Journal of Engineering Mathematics, Vol. 54, No. 4, 2006, pp. 375-388. http://dx.doi.org/10.1007/s10665-005-9023-0
- L. Ling, M. Yamamoto, Y. C. Hon and T. Takeuchi, “Identification of Source Locations in Two-Dimensional Heat Equations,” Inverse Problems, Vol. 22, No. 4, 2006, pp. 1289-1305. http://dx.doi.org/10.1088/0266-5611/22/4/011
- H. M. Park and J. S. Chung, “A Sequential Method of Solving Inverse Natural Convection Problems,” Inverse Problems, Vol. 18, No. 3, 2002, pp. 529-546. http://dx.doi.org/10.1088/0266-5611/18/3/302
- V. S. Ryaben’kii, S. V. Tsynkov and S. V. Utyuzhnikov, “Inverse Source Problem and Active Shielding for Composite Domains,” Applied Mathematics Letters, Vol. 20, No. 5, 2007, pp. 511-515. http://dx.doi.org/10.1016/j.aml.2006.05.019
- L. Yan, C. L. Fu and F. L. Yang, “The Method of Fundamental Solutions for the Inverse Heat Source Problem,” Engineering Analysis with Boundary Elements, Vol. 32, No. 3, 2008, pp. 216-222. http://dx.doi.org/10.1016/j.enganabound.2007.08.002
- L. Yan, F. L. Yang and C. L. Fu, “A Meshless Method for Solving an Inverse Spacewise-Dependent Heat Source Problem,” Journal of Computational Physics, Vol. 228, No. 1, 2009, pp. 123-136. http://dx.doi.org/10.1016/j.jcp.2008.09.001
- F. Yang, “The Truncation Method for Identifying an Unknown Source in the Poisson Equation,” Applied Mathematics and Computation, Vol. 22, 2011, pp. 9334-9339. http://dx.doi.org/10.1016/j.amc.2011.04.017
- F. Yang and C. L. Fu, “The Modified Regularization Method for Identifying the Unknown Source on Poisson Equation,” Applied Mathematical Modelling, Vol. 36, No. 2, 2012, pp. 756-763. http://dx.doi.org/10.1016/j.apm.2011.07.008
- Z. Yi and D. A. Murio, “Source Term Identification in 1-D IHCP,” Computers & Mathematics with Applications, Vol. 47, No. 12, 2004, pp. 1921-1933. http://dx.doi.org/10.1016/j.camwa.2002.11.025
- Z. Y. Zhao and L. You, “A Modified Tikhonov Regularization Method for Identifying an Unknown Source in the Heat Equation,” Acta Mathematica Scientia, 2012.
- A. Neubauer, “An a Posteriori Parameter Choice for Tikhonov Regularization in Hilbert Scales Leading to Optimal Convergence Rates,” SIAM Journal on Numerical Analysis, Vol. 25, No. 6, 1988, pp. 1313-1326. http://dx.doi.org/10.1137/0725074
- H. W. Engl, M. Hanke and A. Neubauer, “Regularization of Inverse Problems,” Springer, Netherlands, 1996. http://dx.doi.org/10.1137/0725074
- F. Natterer, “Error Bounds for Tikhonov Regularization in Hilbert Scales,” Applicable Analysis, Vol. 18, No. 1-2, 1984, pp. 29-37. http://dx.doi.org/10.1080/00036818408839508


