Journal of Applied Mathematics and Physics
Vol.2 No.4(2014), Article ID:43436,6 pages DOI:10.4236/jamp.2014.24002
Conceptual Analysis of a Time-Dependent Double-Diffusive Flow over a Semi-Infinite Vertical Plate
Sunday Ojima Abah, Umar Suleiman, Joseph Enemona Idoko
Department of Mathematics, Statistics and Computer Science, Kaduna Polytechnic, Kaduna, Nigeria
Email: brosoabah@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 4 December 2013; revised 4 January 2014; accepted 10 January 2014
ABSTRACT
This study is devoted to the analysis of a one-dimensional time-dependent double-diffusive flow over a semi-infinite vertical plate, under a convective surface boundary condition. Using similarity variable, the governing nonlinear partial differential equations have been transformed into a set of coupled nonlinear ordinary differential equations, which are solved numerically by using shooting method alongside with Runge-Kutta integration scheme as embedded in Maple software programme. The numerical results of the skin-friction coefficient, the Nusselt and Sherwood numbers are discussed and depicted graphically.
Keywords:Time-Dependent; Double-Diffusive Flow; Semi-Infinite Vertical Plate

1. Introduction
The phenomenon of time-dependent double-diffusive flow has found with wide applications in several areas of science, engineering and technological processes. This flow principle occurs in many areas such as, electronic devices cooling, aerodynamic, cooling of nuclear reactors, drawing of copper wires, extrusion of plastic sheets and cooling of metallic plates.
The problems of time-dependent double-diffusive (mass and heat) flow over a semi-infinite vertical plate have been studied extensively by many researchers.
Soundalgekar and Ganesan [1] investigated transient free convective flow past a semi-infinite vertical plate with mass transfer, and analyzed the finite difference of transient free convection with mass transfer of an isothermal vertical flat plate. Elbashbeshy and Ibrahim [2] investigated the steady free convection flow with variable viscosity and thermal diffusivity along a vertical plate. Takhar et al. [3] examined transient free convection past a semi-infinite vertical plate with variable surface temperature. Rani [4] presented the natural convection flow over an isothermal semi-infinite vertical cylinder with effects of variable viscosity and thermal conductivity. Ishak et al. [5] analyzed MHD mixed convective boundary layer flow towards a stretching vertical surface with constant wall temperature. They stated that, such a flow problem occurs in many industrial and technological applications. Gaur [6] studied the effects of varying viscosity and thermal conductivity on steady free convective flow and heat transfer along an isothermal vertical plate in the presence of heat sink. Aziz [7] investigated similarity solution for laminar thermal boundary layer over a flat plate with a convective surface boundary condition. Makinde and Olanrewaju [8] studied buoyancy effects on thermal boundary layer over a vertical plate with a convective surface boundary condition. Aiyesimi et al. [9] investigated the two-dimensional case of hydromagnetic free convective heat and mass transfer flow over a stretching vertical plate with suction. Abah et al. [10] analyzed numerically the effect of free convection heat and mass transfer on unsteady boundary layer flow past a vertical plate.
In the study, the governing equations were transformed to ordinary differential equation using similarity transformation method and then solved using Maple software programme.
2. Mathematical Formulation
A time-dependent one dimensional double-diffusive (mass and heat transfer) flow of a viscous, incompressible fluid over a semi-infinite vertical plate is considered. The x-axis is taken along the vertical semi-infinite plate in the upward direction and the y-axis is normal to the plate. The governing equation of the flow under the Boussinesq’s approximation is based on the following partial differential equations:
Continuity Equation
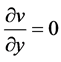 (1)
(1)
Momentum Equation
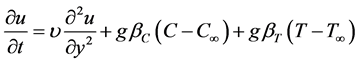 (2)
(2)
Mass Transfer Equation
 (3)
(3)
Heat Transfer Equation
 (4)
(4)
The appropriate boundary conditions for this flow are,
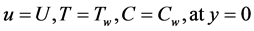 (5)
(5)
 (6)
(6)
Nomenclatures
(μ, ν) = velocity components, (x, y) = coordinates, t = time, T = temperatureTw = wall temperature, T∞ = free stream temperature, υ = kinematic viscosity, g = gravityβT = heat transfer coefficient, βC = mass transfer coefficient, C = concentrationCw = wall concentration, C∞ = free stream concentration, α = thermal diffusion and D = coefficient of mass diffusion.
We now introduce the following dimensionless variables and quantities in order to transform the governing momentum, energy and concentration equations and the boundary conditions from partial differential equations to ordinary differential equations using similarity transformation method: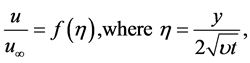
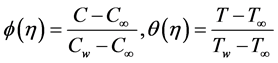 ,
,
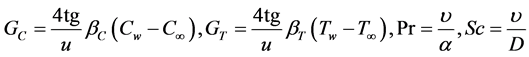
Substituting the above dimensionless quantities into the governing Equations (1)-(4) and the boundary conditions, we obtain the following dimensionless form, ordinary differential equation:
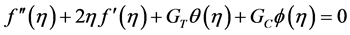 (7)
(7)
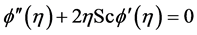 (8)
(8)
 (9)
(9)
with the transformed boundary conditions as
 (10)
(10)
3. Numerical Solutions
The coupled system of non-linear ordinary differential Equations (7)-(9) together with the boundary conditions (10) are solved numerically by using the shooting iteration technique along with Runge-Kutta initial value solver. The numerical computations were carried out using a program which uses a symbolic and computational computer language MAPLE, the software package used is Maple 15.
The numerical results of the Skin-friction coefficient, the Nusselt and Sherwood numbers are depicted graphically in Figures 1 to 4 in the form of velocity, temperature and concentration profiles to illustrate the influence of the studied parameters on the flow.
4. Discussion of the Results
The velocity profiles in the boundary layer for various values of Thermal Grashof number is shown in Figure 1. Increase in the value of Thermal Grashof number produces an increase in the velocity flow.
The Velocity profiles for various values of concentration Grashof number is depicted in Figure 2. It is also seen that the velocity increases with the increase of the concentration Grashof number. From Figures 1 and 2, it is glaring that, as the Grashof number increases, the fluid velocity increases, reaching its peak value within the boundary layer and then decreases monotonically to the free stream zero value far away from the plate surface satisfying the far field boundary condition. From these figures, it is obvious that the buoyancy forces parameters enhance the fluid velocity thereby increasing the momentum boundary layer thickness.
Figure 3 shows the effect of Prandtl number on the temperature profiles. It is perceived that as the Prandtl number increases it results in a lower average temperature within the boundary layer. Therefore there is a reduction in temperature with increase in the Prandtl number.
The influence of the Schmidt number on the concentration is illustrated in Figure 4. It indicates the concentration profiles showing the effect of Schmidt number. It is observed that concentration profiles decrease very rapidly with the increase of Schmidt number. Therefore, as Schmidt number increases the concentration decreases.
5. Conclusions
A theoretical study of a Time-Dependent Double-Diffusive Flow over a Semi-infinite Vertical Plate has been carried out. The nonlinear equations governing the problem are solved numerically by applying Runge-Kutta as well as the shooting method as embedded in Maple software. Numerical investigations showing the impact of the various physical parameters on the velocity, temperature and concentration profile were performed leading to the following:
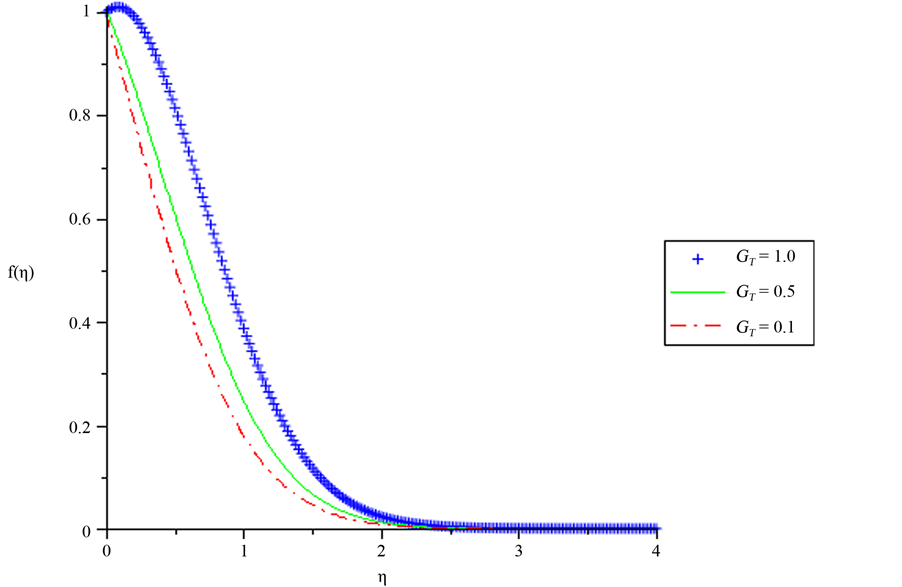
Figure 1. Velocity profiles for various values of Thermal Grashof number, GT. When GC = 0.1, Pr = 0.72, SC = 0.24.
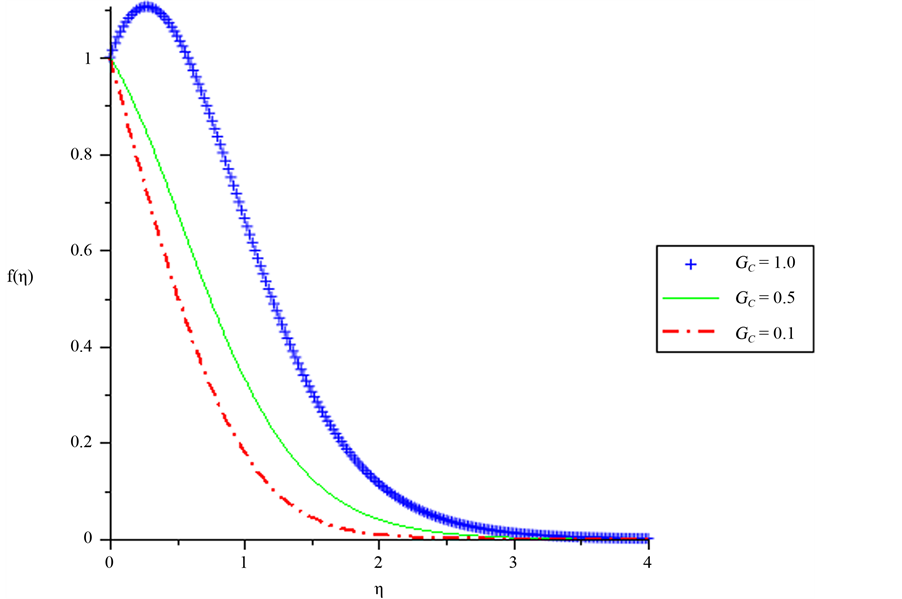
Figure 2. Velocity profiles for various values of Concentration Grashof number, GC. When GT = 0.1, Pr = 0.72, SC = 0.24.

Figure 3. Temperature profiles for various values of Prandtl number, Pr. When GT = GC = 0.1, SC = 0.24.

Figure 4. Concentration profiles for various values of Schmidt number, SC. When GT = GC = 0.1, Pr = 0.72.
1) A rise in the thermal Grashof and the concentration Grashof number leads to an increase in the velocity profile.
2) An increase in the Prandtl number leads to a decrease in the temperature profile.
3) A rise in the Schmidt number leads to a decrease in the concentration profile.
References
- Soundalgekar, V.M. and Ganesan, P. (1980) Transient Free Convective Flow Past a Semi-Infinite Vertical Plate with Mass Transfer. Journal of Energy Heat and Mass Transfer, 2, 83.
- Elbashbeshy, E.M.A. and Ibrahim, F.N. (1993) Steady Free Convection Flow with Variable Viscosity and Thermal Diffusivity along a Vertical Plate. Journal of Physics: Applied Physics, 26, 2137.
- Takhar, H.S., Ganesan, P., Ekambavanan, K. and Soundalgekar, V.M. (1997) Transient Free Convection Past a SemiInfinite Vertical Plate with Variable Surface Temperature. International Journal of Numerical Methods for Heat and Fluid Flow, 7, 280-296. http://dx.doi.org/10.1108/09615539710165804
- Rani, H.P. and Kim, C.N. (2008) Transient Convection on Vertical Cylinder with Variable Viscosity and Thermal Conductivity. Journal of Thermo Physics and Heat Transfer, 22, 254-261. http://dx.doi.org/10.2514/1.32501
- Ishak, A., Nazar, R. and Pop, I. (2008) Hydromagnetic Flow and Heat Transfer Adjacent to a Stretching Vertical Sheet. Heat and Mass Transfer, 44, 921-927. http://dx.doi.org/10.1007/s00231-007-0322-z
- Gaur, P. and Mahanti, N.C. (2009) The Effects of Varying Viscosity and Thermal Conductivity on Steady Free Convective Flow and Heat Transfer along an Isothermal Vertical Plate in the Presence of Heat Sink. Journal of Applied Fluid Mechanics, 2, 23-28.
- Aziz, A. (2009) A Similarity Solution for Laminar Thermal Boundary Layer over a Flat Plate with a Convective Surface Boundary Condition. Communications in Nonlinear Science and Numerical Simulation, 14, 1064-1068. http://dx.doi.org/10.1016/j.cnsns.2008.05.003
- Makinde, O.D. and Olanrewaju, P.O. (2010) Buoyancy Effects on Thermal Boundary Layer over a Vertical Plate with a Convective Surface Boundary Condition. Journal of Fluids Engineering, 132, 044502. http://dx.doi.org/10.1115/1.4001386
- Aiyesimi, Y.M., Abah, S.O. and Okedayo, G.T. (2011) The Analysis of Hydromagnetic Free Convection Heat and Mass Transfer Flow over a Stretching Vertical Plate with Suction. American Journal of Computational and Applied Mathematics, 1, 20-26. http://dx.doi.org/10.5923/j.ajcam.20110101.05
- Abah, S.O., Eletta, B.E. and Omale, S.O. (2012) The Numerical Analysis of the Effect of Free Convection Heat and Mass Transfer on the Unsteady Boundary Layer Flow Past a Vertical Plate. International Journal of Theoretical and Mathematical Physics, 2, 33-36. http://dx.doi.org/10.5923/j.ijtmp.20120203.02

