Received 5 August 2015; accepted 9 October 2015; published 12 October 2015

ABSTRACT

In order to continuously promote the polar sample resource services in China and effectively guide the users to access such information as needed, a fuzzy algorithm based on DBpedia has been proposed through the analysis of the characteristics of the query recommendations in search engines, namely, to search similar entry queues by constructing a DBpedia category tree, then use the fuzzy matching algorithm to work out the entry similarity, and then present the example query applications of this algorithm on the resource-sharing platform of polar samples. Comparing the traditional literal character matching method and DBpedia semantic similarity algorithm, the experimental results show that the fuzzy query algorithm based on DBpedia features has a higher search accuracy rate, stronger anti-interference capability, and more flexible algorithm use by virtue of its fuzzy weight adjustment.

Keywords:

Search Engine, Fuzzy Query, Semantic Similarity, Wiki

1. Introduction

As one of the most important modules of information platforms, each search engine has its query recommendation almost as a standard function for its search module. In particular, when the users are not clear about their search objects, the relevant search results given by the search engine can effectively guide the users to gradually get access to the information they need [1] . During the past decade, the query recommendation technology has obtained fairly satisfactory results in e-commerce platforms; therefore, in order to improve the value of scientific data, this paper examines the application of the query recommendation technology on resource-sharing platform of polar samples (BIRDS). It provides information on major samples collected in the polar regions during previous Chinese polar expeditions with large numbers of valuable samples available, including snow, ice cores, flora and fauna, meteorites, sediments, and rocks. Since the establishment of BIRDS in 2006, it has released 7058 resources, 12,279 pictures and 6.4 GB data. On average, every day it is visited by 895 users from 187 countries with 112 million clicks and 16.6 TB content downloads. However, most users came from the cooperated institutes of BIRDS, and the average PV (pages view) per day per user normally was less than 20. In order to further promote the polar sample resource services in China, to provide more samples and relevant information to scientists who have made an attempt to carry out related polar research but without access to filed study, and to improve the utilization efficiency of polar sample resources, this paper has designed a fuzzy query recommendation algorithm based on Wikipedia knowledge database and applied it to BIRDS [2] .

Scientific data platforms have a relatively smaller number of users than e-commerce platforms and thus have a simpler user log; thereby this paper presents the query recommendation [3] based on contents. In addition, this paper has fully considered the fact that search engine is one of the most important factors of information platforms, as well as the character or word association characteristics [4] to have proposed the DBpedia-based fuzzy query algorithm, namely, to search similar entry queues by constructing a DBpedia category tree, then use the fuzzy matching algorithm to work out the entry similarity, and then present the example query applications of this algorithm on BIRDS.

In the past 10 years, many scientific data platforms have offered query recommendation services which received good effect, but this fuzzy query recommendation algorithm based on DBpedia is first presented and applied on scientific data platforms especially on polar data sharing systems. After the application on BIRDS, the platform’s daily users increased to thousands, and the daily PV per user was stabled at about 15. More platform visit data show the algorithm proposed better effect than normal query recommendation algorithm.

2. Algorithm of Category Tree on a Knowledge Database

2.1. Construction of Semantically Similar Category Tree

The construction of a knowledge database is a complicated task involving many disciplines. The associated database [5] - [7] constructed in this paper based on DBpedia has the following characteristics:

Ÿ Its entries are based on Wikipedia, and are able to develop along with changes of Wikipedia.

Ÿ It has extracted structured data from Wikipedia and converted such data into the form of Linked Data.

Ÿ Its knowledge database uses the form of ontological construction to organize the entries.

Ÿ It has an open API interface, enabling the machine to understand such structural data.

The DBpedia body mainly consists of four types of system structures [8] :

(1) “part-of” relationship, indicating the relationship between the part and the whole of a concept.

(2) “kind-of” relationship, indicating an integrated relationship between concepts.

(3) “instance-of” relationship, indicating the relationship between the concept and its instances.

(4) “attribute-of” relationship, indicating that one concept is the attribute of another concept.

The method in this paper only uses the relationship between “concepts” and “categories” to construct a category tree. For instance, in Chinese Wikipedia, the free encyclopedia:

Skua category: Gull passerine|Stercorariidae.

Stercorariidae category: Gull passerine.

Gull passerine category: Birds|Charadriiformes.

Emperor penguin category: IUCN threatened species|Antarctica|Spheniscidae.

Spheniscidae category: birds|Sphenisciformes|Spheniscidae.

Sphenisciformes category: birds|Sphenisciformes|Spheniscidae.

Finally a knowledge database as below can be obtained:

Skua -> Stercorariidae -> Gull passerine -> Birds.

Emperor penguin -> Spheniscidae -> Sphenisciformes -> Birds.

In the process of the category tree extraction, it is particularly important to set the height of the category tree; if it is too high, the traversal speed will be influenced; if too low, the matching effect will be reduced.

2.2. Construct a Proper Height for the Category Tree

A category tree’s error rate will be quite high if it is constructed too small. On the other hand, if the tree is too big, the apparent error rate obtained by means of learning set test is very small, but its true error rate may still be relatively large. Therefore, we need to construct a tree of a proper/appropriate size to minimize the real error rate.

The purpose/aim of decision tree learning is to obtain a simple tree with a strong predictive capacity. When the tree is in its full growth, its predictive capacity will be reduced. In order to solve this problem, we need to obtain a tree of the proper/appropriate size. In generally, there are two methods available.

Method-1: Define the conditions that the tree will stop growing.

1) Partition the number of instances to the minimum. When the size of the data subset corresponding to the current node is smaller than the number of specified minimum partition instances, no further partition is needed even though they do not belong to the same category.

2) Partition threshold value. When the difference between the value obtained by means of the applied partition method and the value of its parent node is smaller than the specified threshold value, no further partition is needed.

3) Maximize tree depth. When the length of further partition will exceed the maximal tree depth, stop partitioning.

Method-2: Carry out pruning after a complete decision tree is generated by evaluating subtrees. The entire decision trees will perform better if a subtree is removed, then the subset is pruned. Specifically, the implementing process in the Breiman CART [9] are as follows:

1) Tree construction

The decision tree is made up of the data sets partitioned by attribute values, and thereby needs to define the measurement partitioned by attribute, namely, according to this measurement, the optimal partitioning attributes for current data subset can be worked out.

When the fuzzy function of calculation cost for node has been selected, during the process of the tree growth, we are always trying to find an optimal bifurcation value to partition the samples in the node, so that the cost could be minimized. The fuzzy function 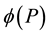is used to represent the fuzzy degree of the tree node t or error partition index, namely:

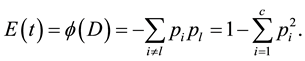(1)

Here, 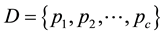is a decision set, c denotes the number of the decision-making categories in the decision set, indicates the proportion of the i^th decision-making category in the decision set D and.

In the bifurcation tree of the CART algorithm architecture, the amount of changes of fuzzy degree due to bifurcation is as follows:

(2)

where, t is the bifurcation node; 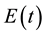is the fuzzy degree of the node t; and 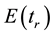are the fuzzy degree of the left and right bifurcation node, respectively; 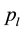and 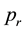denote the percentage of the node t in the left and right bifurcation samples, respectively. For bifurcation of each internal node t, take the largest change of fuzzy degree in all possible bifurcation ways of t. For other nodes, repeat the same search process.

2) Pruning

The large scale trees are generated by the above algorithm and its apparent error rate is very small, but its true error rate may still be relatively large. We must construct a tree with a small true error rate by means of the pruning technique. We use a certain algorithm to prune the branches of this tree continuously. During the pruning process, we will obtain a list of decresing trees to form a sequence of pruned trees, and each tree in this sequence will have a smaller apparent error rate [9] compared with other subtrees of the same size, and then we can conclude that this sequence is an optimal one. The bifurcation tree can be pruned on the basis of the minimal cost complexity principle as below:

In general, a tree can be expressed by T, the subtree with the root node of t is expressed by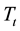, then the pruned subtree 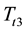will shrink into a terminal node t3, the pruned tree can be expressed as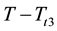, and there is the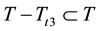, which is the subset of T. Use 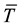to express the terminal node set in the trees T, and the number of the corresponding terminal nodes is. The impurity index of the tree T is defined as follows:

(3)

denotes the fuzzy index of the tree node t or the square error of the fitting node data set of the node t in the Equation (3), and the error index is the fuzzy function.

The pruning principle of the decision tree, namely, the cost complexity measurement is displayed as:

(4)

where denotes a linear combination of the tree impurity index cost and its complexity. Therein, a is the complexity parameter resulted from the complexity of a tree and indicates the number of the terminal nodes for the tree T.

To find the next smallest tree of the tree T: For each internal node t of the tree T, we need to work out the value a of the penalty factor for the next tree wrongly partitioned, and label the value as, which is the ratio between the change amount of the error index before and after the current tree is pruned and the change of the terminal node number:

(5)

The node we need to select is an internal node with minimal. The whole tree pruning process is to calculate, then seek the smallest, and then select as the next pruning object.

For each given value a, a smallest tree can always be found based on the corresponding to the measurement of its cost complexity:

(6)

When the value a increases, always remains smallest until it reaches a jump point, and then the tree becomes a new smallest tree.

After the smallest tree is determined, its height can be defined as, where is the number of layers of the final leaf nodes while is the number of layers of the root nodes.

For such cases in this paper, we can work out the appropriate height of a tree as according to the above algorithm.

3. Similarity Algorithm

The similar degree of traditional category tree is mainly calculated through the following two methods: character direct search method and vector included angle cosine calculation method. However, these two methods are oversimplified and thus the similarity is seriously affected. Therefore, based on the character search method, this paper has proposed a fuzzy query algorithm based on DBpedia.

3.1. Literal Character Matching Method (CCQ)

Literal character matching method is the easiest method, it judges the similarity by the proportionality of common words on two words. For example, there is one common word between adelie penguins and emperor penguin, then the matching value is 0.5.

Algorithm:

First, get all samples’ name from database, named Word₁, Word₂, … Word_i, …, Word_n;

Second, calculate each correlation for word_i, and the value is correlation [word_j, word_i] = Max (length (common words (word_j, word_i))/lengh (word_i), length (common words (Pinyin (word_j), Pinyin (word_i)))/lengh (Pinyin (word_i))).

3.2. Fuzzy Query Algorithm (WIKIFQ)

If the search contents are classified according to such attributes of a word or a phrase as pronunciation, meaning and relevance, refer to the concrete fuzzy query algorithm [10] .

1) Classification of the query contents

Firstly, the samples to be queried are classified appropriately. The query criteria are: the smaller distance between the example that belongs to a certain category and the center within the category is the better; the larger distance that is from the center among categories is the better. According to the attributes of each category, the

average value of each category is calculated as the category center. Assume is the membership function of the kth sample to the ith category, and,. Assume is the distance between the sample and the center of the ith category, and m > 1 is a fuzzy

weighted exponent. Define the distances within a category and among categories, to make the distances satisfy that the distance is from the center within the category is smaller, and the distance is from the center among categories is larger.

Define the distance within a category

(7)

Define the distance among categories

(8)

Synthesize the Equations (7) and (8) to define the objective function as

(9)

where, is applicable to a certain i, while is applicable to all i.

An objective finally needs to be classified into a certain kind of problems according to a certain membership degree, so the objective function satisfies a certain constraints as follows:

(10)

According to the objective function, the following conditions should be met: 1) the defined should be inversely proportional to, namely, is a monotone decreasing function about. 2) is a monotone increasing function about the fuzzy weighted exponent m. 3) is the membership degree, so. Moreover, it requires that each category must contain one sample at least, but the sample may not belong to the same category, so is true. 4) Simultaneously, satisfies the Equation (10).

According to 1)-4), can be defined as follows:

(11)

It can be proved that the Equation (11) satisfies the conditions 1)-4).

Under the constraint (10), the minimal value of the Equation (9) can be obtained by iterating repeatedly the Equation (11) to determine the final.

Based on, assume the center of each category is, and it can be calculated as follows:

(12)

2) Character matching query

For a sample x to be queried, calculate the distance between x and the center, select k characters or words that is closest to x, which are represented by respectively. Define an ordered pair, and

is the category which the sample x belongs to:, in which R is a set of samples to be queried, W is a finite set of category, is the ith type content of the partition query content, and n is the number of categories. Then can be calculated as follows:

, where. If, then the sample x belongs to the category.

The above expressions can also be written as:, here, then x belongs to the category,.

3.3. Selection of the Fuzzy Weighted Exponent m

For the Equation (11), when, each in the Equation (11) satisfies or 1, and when, there is no weighted value; when, each satisfies, and the partition is most fuzzy at this time. It is clear that the exponent m directly determines the fuzziness of the classification results.

To classify the search contents, we can use the fuzzy method and algorithm [11] - [13] of target recognition researched by BEZDEK, Lin Qing, Wei Meia and others. The fuzzy degree of classification is defined as follows:

(13)

where, BEZDEK [11]

(14)

A fuzzy decision-making problem is formed by the intersection of a given fuzzy target and a fuzzy constraint, i.e.,

.

In this paper, the fuzzy object of a decision-making problem that a keyword or a word is queried is defined as follows:

(15)

where, is the set of the final determined when the Equation (9) reaches a minimal value. In addition, while completing the content fuzzy classification, this algorithm also requires that the content should be partitioned as clearly as possible in order to correctly distinguish the category membership of each sample. Therefore, the selection of the parameter m is subject to another constraint, namely, the selected value can not make the classification results of the fuzzy classification algorithm overly fuzzy. The partition fuzzy degree is a good measurement to evaluate fuzzy classification to partition fuzziness. As a result, the fuzzy constraint of the decision that the parameter m is preferred is as follows:

(16)

When and are treated as fuzzy sets, they can be characterized by their membership functions respectively. In order to ensure that the membership functions of the fuzzy object and the fuzzy constraint have the same increasing or decreasing extent, the membership functions of and can be defined respectively as follows:

(17)

(18)

The membership function of fuzzy decision can be expressed as, and the final decision-making result is the solution to satisfy.

Consequently, the optimal weighted index m^* is the m value corresponding to the maximum membership degree of the intersection of fuzzy subsets corresponding to the fuzzy object and fuzzy constraint, respectively. The optimal weighted index m^* can be obtained by the following formula:

(19)

The m^* obtained based on the Formula (19) will be able to ensure that the classified objective function and the classified partition fuzziness could be minimized by a larger membership degree, so that the fuzzy classification achieved by the fuzzy classification algorithm could not only express the similar information among samples, but also ensure the clarity of the sample classification. Therefore, a corresponding better fuzzy classification result will be obtained.

4. Experiment

4.1. Data Processing

1) Construct a DBpedia Database

A data rather large in amount cannot be indexed or retrieved if placed directly in a document, so a MYSQL database should be built. Download the XML dump file of 2013 November from Chinese Wikipedia, extract the three files to get zhwiki-latest-categorylinks.sql, zhwiki-latest-pages.sql and zhwiki-latest-redirect.sql (with the total of 1.34 GB), and import such files into the DBpedia Chinese entry database already obtained with approximately 3,102,000 page records, 315,000 category records and 7,736,000 categorylinks records.

2) Get N entries from the database of BIRDS [14] . N = Random (50 - 100)

3) Extract the category tree from DBpedia and then form a weight matrix [15] [16] . The code for a category tree of an individual entry is shown in Figure 1 and Figure 2.

4) Superimpose the fuzzy matching algorithm to get similarity

In the experiment, take the fuzzy weighted exponent.

5) Test environment

CPU: 2.5 GHZ × 2 core

Memory: 4.0 GB

OS: Windows 7 - 64 bit

4.2. Experimental Results

In order to verify the efficiency of this algorithm, we compare it with the traditional literal string matching algorithm and DBpedia semanteme-based algorithm (Table 1). The results indicate that the fuzzy matching algorithm is more accurate than other algorithms in terms of semantic analysis, and is even capable of detecting certain relationships between two seemingly different words.

4.3. Discussion

From the test result shown in Table 1, we can conclude that WIKIFQA method can detect similar data more efficiently and more accurately. After the application of the WIKIFQA on 2013 years, users have received more convenient service, and the value of PV, IP increased also (Figure 3).

But the algorithm is dependent on wiki database too much, and its accuracy is mostly affected by the quantity and quality of Wikipedia pages. To improve the accuracy, we have to update the database quarterly automatically.

5. Conclusion

This paper provides a DBpedia-based fuzzy query algorithm and gives the feature extraction method for fuzzy algorithm eigenvalue and implementation of semantic matching algorithm based on the analysis of the characteristics of the polar sample data and Wikipedia Chinese data. The experimental results show that this WIKIFQA

method can detect similar data more efficiently and more accurately to improve data accuracy, compared with the traditional literal string matching method and DBpedia semantic similarity algorithm. Also, the algorithm application on BIRDS proves its applicability and convenience.

Foundation

This work is supported by National Ocean Public Benefit Research Foundation(201305035); Key Laboratory of Digital Ocean, SOA (KLD0201408) respectively, Platform for Basic Conditions of the Ministry of Science and Technology (2005DKA21406); National postdoctoral science foundation (2013M531120); Project of Henan Province Science and Technology (No. 142300410247); Project of Henan Province Education Department (14A413002); Project of Zhengzhou Scientific and Technology Department (131PPTGG411-4).

Cite this paper

WenfangCheng,Qing’eWu,XiaoCheng,JieZhang,ZhuanlingSong,11, (2015) DBpedia-Based Fuzzy Query Recommenda-tion Algorithm and Its Applications in the Resource-Sharing Platform of Polar Samples. International Journal of Intelligence Science,05,196-207. doi: 10.4236/ijis.2015.55017

References

NOTES

^*Corresponding author.