International Journal of Intelligence Science Vol.05 No.03(2015),
Article ID:55014,12 pages
10.4236/ijis.2015.53013
A Data-Placement Strategy Based on Genetic Algorithm in Cloud Computing
Qiang Xu*, Zhengquan Xu, Tao Wang
State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan, China
Email: *xuqiangwhu@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 January 2015; accepted 20 March 2015; published 25 March 2015
ABSTRACT
With the development of Computerized Business Application, the amount of data is increasing exponentially. Cloud computing provides high performance computing resources and mass storage resources for massive data processing. In distributed cloud computing systems, data intensive computing can lead to data scheduling between data centers. Reasonable data placement can reduce data scheduling between the data centers effectively, and improve the data acquisition efficiency of users. In this paper, the mathematical model of data scheduling between data centers is built. By means of the global optimization ability of the genetic algorithm, generational evolution produces better approximate solution, and gets the best approximation of the data placement at last. The experimental results show that genetic algorithm can effectively work out the approximate optimal data placement, and minimize data scheduling between data centers.
Keywords:
Cloud Computing, Data Placement, Genetic Algorithm, Data Scheduling

1. Introduction
With the increase of network equipment as well as the development of the Internet, data generation and storage capacity are growing explosively; data centers will face unpredictable visitor volume [1] . The large amount of data and the complex data structures make traditional database management unable to meet the requirements of big data storage and management. The distributed architecture of cloud computing can provide high-perfor- mance computing resources and mass storage resources [2] [3] . However, in distributed cloud computing system, data-intensive computing needs to deal with large amounts of data; in multi-data center environment, some data must be placed in a specified data center and cannot be moved. A computation may process datasets from different data centers, then data scheduling between data centers will occur inevitably. Because of the huge size of data and limited network bandwidth, data scheduling between data centers has become a huge problem. The datasets processed simultaneously by a computation should be placed in the same data center, then almost all data processing is completed locally; that is the basic idea of the paper.
Much work has been developed about the data placement in distributed system and they can be divided into two types in general: static data placement and dynamic data placement. Most static data placement algorithms require complete knowledge of the workload statistics such as service times and access rates of all the files. Dynamic data placement algorithms [4] [5] , generate file-disk allocation schemes on-line to adapt to varying workload patterns without a prior knowledge of the files to be assigned in the future. Dynamic data placement strategies update the placement strategy potentially upon every request. Obviously, they are effective when the data size is relatively small such as the case in web proxy caching. However, in applications like distributed video servers, dynamic schemes become less useful [6] [7] . In data-intensive computing, if multiple computations jointly process multiple datasets in a frequent way, these datasets are supposed to be correlative with each other. Some researches on data placement are based on data correlation [8] -[12] ; however, the definitions of data correlation are not reasonable, and no effective method is proposed to reduce the data scheduling between the data centers. Replica strategy [13] is an effective measure to reduce the data scheduling and has earned widespread research interests, and it is also based on data placement.
This paper presents a genetic algorithm-based data placement strategy. First, a mathematical model of data scheduling between the data centers in cloud computing is built, and the fitness function based on the objective function is defined to evaluate the fitness of each individual in a population. After the initial population generated in accordance with the principle of survival of the fittest, the evolution of each generation produces better approximate solution. In every generation, roulette-wheel selection is used to choose the appropriate individuals with high fitness value and the individuals with low fitness value are eliminated. With the crossover and mutation operations, we change the placement location of datasets. Under the principle of survival of the fittest, the optimal individual can be found during the evolution.
2. Data Placement Strategy in Cloud Computing
In cloud computing systems, data storage typically achieves petabytes magnitude scale, complex and diverse data structures, high requirements of data service type and level have brought great pressure to data management [14] . Cloud systems have the characteristics of data-intensive and compute-intensive, and the concurrent executions of large-scale computations in the systems require massive data and generate amass intermediate data. This paper attempts to establish a model of data scheduling between data centers that provides an accurate mathematical theoretical basis for data placement.
2.1. The Model of Data Scheduling between Data Centers in Cloud Computing
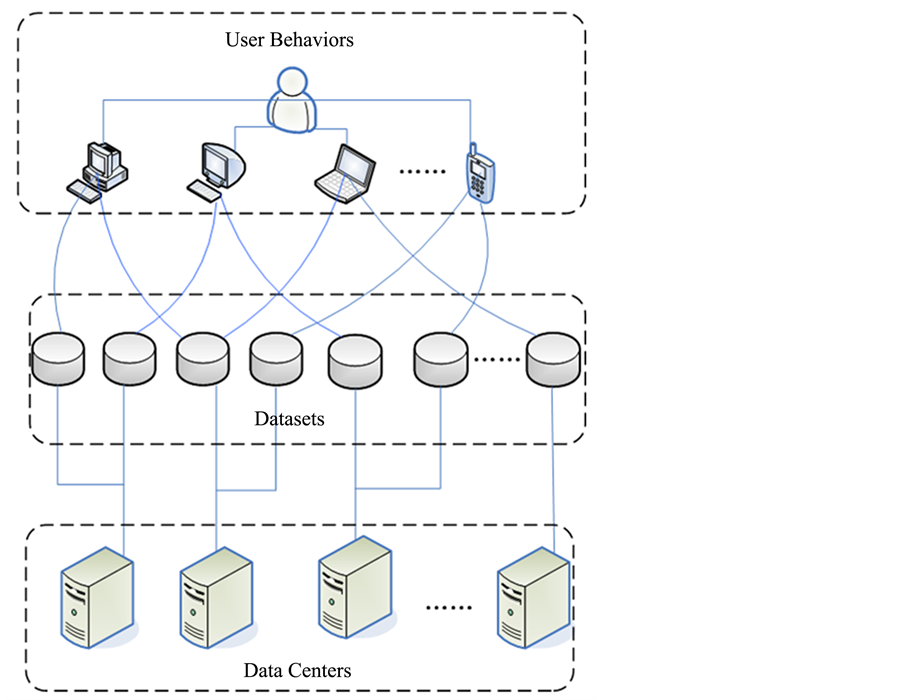
Assuming that a cloud computing system is composed by l data centers, and data are divided into n different datasets based on their inherent properties. When user request for data resources, we assign their different operations into m computations. If performing a computation needs to process datasets in different data centers, data scheduling between data center happen. The physical model of data scheduling between data center is showed in Figure 1.
Assuming that the collection of datasets stored in a distributed cloud computing system is:
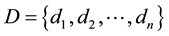 (1)
(1)
where n is the number of datasets and the size of dataset
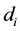 is
is
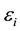 ,
,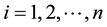 .
.
The l data centers in the system are denoted as:
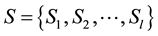 (2)
(2)
The basic capacity of data center Sk is Sk.
The m computations in the system are denoted as:
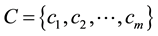 (3)
(3)
Figure 1. Physical model of data scheduling between data center.
The execution frequencies of each computation can be denoted as:
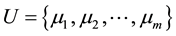 (4)
(4)
where
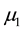 is the execution frequency of computation 𝑐𝑖 in unit interval.
is the execution frequency of computation 𝑐𝑖 in unit interval.
We define a processing factor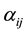 , where
, where
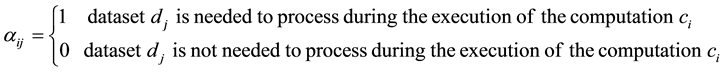 (5)
(5)
Thus we can get the association matrix of the computation set C and the datasets D, which is denoted as:
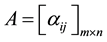 (6)
(6)
Data placement is to distribute datasets into each data center. In this paper, data
replica is out of consideration. Similarly, we define a placement factor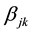 , where
, where
 (7)
(7)
Thus we can get the association matrix (placement matrix) of the datasets D and the data center S, denoted as:
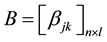 (8)
(8)
Matrix B reflects the status of the datasets D stored in the data centers S. We can easily find that the sum of the elements of each row in matrix B is 1,
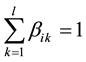 (9)
(9)
The sum of the elements of the kth column in matrix B is the number of datasets stored in the data center Sk, when we place datasets into data center Sk, the stored data size should not exceed the basic capacity of Sk, thus
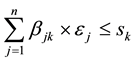
Define a matrix Z, denoted as
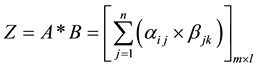
Suppose
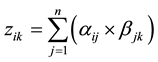
then matrix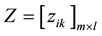
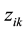
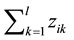
of accessing all data centers during the execution of the computation ci, also is the number of datasets processed
during the execution of the computation ci. The sum of elements in each
column, denoted as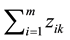
number of the datasets processed in data center Sk when all the computations
are performed one time. Define a function
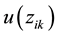

Then the number of data centers accessed during the execution of computation ci
is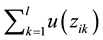
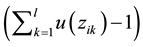
is B, the total number of data scheduling during the execution of all computations in the system in unit interval can be expressed as:
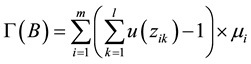
Our objective is to find the optimal data placement solution B* that
minimize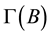
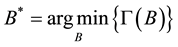
2.2. Genetic Algorithm
In the issue of big data placement, the solution space is very huge, and B matrices are sparsely distributed in it. There are a lot of traditional optimization algorithms, such as the exhaustive search algorithm, Monte Carlo algorithm, Genetic algorithm, Simulated Annealing algorithm and so on. In this paper, different algorithms are compared to find the optimal data placement solution B*.
Exhaustive search algorithm is a direct way to search the optimal placement matrix.
It works out all possible data placement B matrices, then traverses to find the
smallest Г(B), at this point the placement matrix is the optimal solution. However,
the computation complexity of exhaustive search algorithm is very high which approximates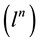
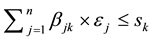
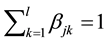
NP-hard problem. So the exhaustive search algorithm is only available when the number of datasets is small.
Monte Carlo algorithm is based on probability theory and statistics methods. In big data placement based on Mont Carlo algorithm, we randomly generate a certain number of B matrices as a sample, then calculate data scheduling between data centers on each sample matrix B, and find out the placement matrix with the minimum data scheduling. Compared with the exhaustive search algorithm, the computation complexity of Monte Carlo algorithm is improved, however, B matrices are sparsely distributed in the solution space, the search efficiency of Monte Carlo algorithm is still not high. It has a strong regularity as well as constraint conditions to generate placement matrices, genetic algorithm uses a strategy of a directed search through a problem state space from a variety of points in that space [15] , it is more efficient and robust than the random search, enumerative or calculus based techniques [16] . Therefore, the use of genetic algorithm can deal with this problem.
Genetic algorithm is an adaptive search and optimization algorithm based on the mechanics of natural selection and natural genetics [17] [18] . A population of candidate solutions (called individuals) to an optimization problem is evolved toward better solutions [19] [20] . In genetic algorithm, the degree of adaptation of each individual to the environment is represented by fitness. Individual with high fitness has a greater chance to survive. In each generation, the fitness value of each individual in the population is evaluated, individuals with higher fitness value are stochastically selected from the current population, then crossover and mutation operator are manipulated to form a new generation. The new generation of candidate solutions is then used in the next iteration of the algorithm.
1) Encoding
In the issue of genetic algorithm-based data placement, the placement of datasets in data centers is represented by matrix B, because of the string structure of matrix, the placement matrix is directly manipulated as genotype in genetic algorithm.
2) Individual and population
An individual is a point in the searching space, the collection of placement matrices is the searching space of the data placement.
A population consists of several individuals and it is a subset of the whole searching space.
3) Fitness function
Fitness function is the evaluation function to guide the search in genetic algorithm [21] [22] . In the issue of genetic algorithm-based data placement, the objective function is denoted as Г(B), and the fitness function is the reciprocal of the objective function, that is 𝐹 = 1/Г(B).
4) Genetic operators
① Selection: Roulette wheel selection is a genetic operator used in genetic algorithms for selecting potentially useful solutions for recombination [23] , chromosomes with higher fitness level are more likely to be selected. The steps of Roulette wheel selection are as follows:
Step 1: Obtain the fitness value f(i) of each individual in a N size population.
Step 2: Suppose there is an individual 𝑘 and its probability of being selected
is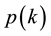
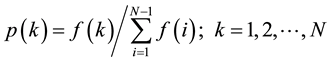
Step 3: Suppose 𝑞(0) = 0,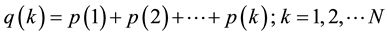
Step 4: Generate a random number r (0 ≤ r < 1), if q(k‒1) < r < q(k), then individual k is selected.
② Crossover: In Genetic algorithm, crossover operator is used to vary the programming of a chromosome or chromosomes from one generation to the next [24] . Before crossover, individuals in the population should be paired randomly and choose the crossover point and then exchange some genes. Assume that B1 pairs with B2, generate two random number r1, r2 (0 < r1 < r2 < n) as the crossover point, then exchange the genes between the two points, the resulting organisms are the children. Figure 2 is the schematic of the two-point crossover in a 4*3 placement matrix.
③ Mutation: Mutation alters one or more genes in a chromosome from its initial state.
For a binary string, if the genome bit is 1, it is changed to 0 and vice versa.
When the mutation operator is used in a placement matrix, a random number r1
(0 ≤ r1 < n) is generated, and the placement of dataset
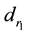
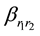
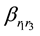
Figure 2. Perform two-point crossover operator on placement matrixes.
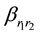
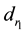
2.3. Process of Data Placement Based on Genetic Algorithm
Step 1: Determine the size of population (G), crossover rate (Pc) and mutation rate (Pm) according to the actual situation.
Step 2: Generate the initial population: Initial population BG (0) consists of G
placement matrices. To generate an individual matrix Bi, all the elements
of the matrix is set to 0, then n random numbers

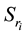
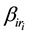
Step 3: Calculate the fitness of each individual in population BG(T), T = 0, 1,
2, ×××, MaxGen: Get matrix Z by matrix multiplication, that is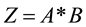
the number of data scheduling is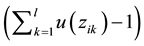
ing in
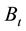
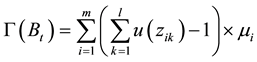
Step 4: Calculate the number of data scheduling Г(Bt) of each individual in population BG(T), the fitness value of Bt is denoted as 𝐹 = 1/Г(Bt). After the fitness value of each individual and the probabilities being chosen are calculated, select G individuals from BG(T) by roulette wheel selection.
Step 5: Perform crossover operator on the selected placement matrices: Crossover rate Pc represents the percentage of the chromosomes taking part in the crossover operation [18] [19] . The process of crossover is as follows:
Figure 3. Perform mutation operator on placement matrixes.
Step 6: Perform mutation operator on the selected placement matrices: Mutationrate Pm represents the percentage of the chromosomes taking part in the mutation operation [25] [26] . If the size of a population is G and each individual has n genes, the number of genes to be mutated is G*n*Pm. We can generate random number (0 ≤ 𝑟 ≤ 1), if r < Pm, the corresponding gene is to be mutated. The process of mutation is as follows:
Step 7: Abandon the new individuals that do not meet the requirements of the storage capacity limitation
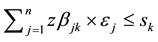
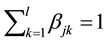
and continue the evolution, otherwise terminate the iteration and find the individual with highest fitness, the individual is regard as the approximate optimal solution.
Step 8: From the definition of placement factor
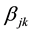
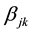
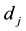
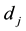
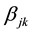
3. Experiment and Simulation
3.1. Simulation Environment
To test the data placement strategy based on genetic algorithm proposed in this paper, a “digital city” oriented data storage and access platform is constructed. The platform is composed of 20 Dell Power Edge T410 servers. Each of them has 8 Intel Xeon E5606 CPU (2.13 GHz), 16G DDR3 memory and 3TB SATA disk. Every server acts as a data center and we deploy VMware and independent Hadoop distributed file system on each data center. Under the environment of Gigabit Ethernet, users can submit data and perform computations through digital city application demonstration system developed by Flex 4.5.
3.2. Simulation Result and Analysis
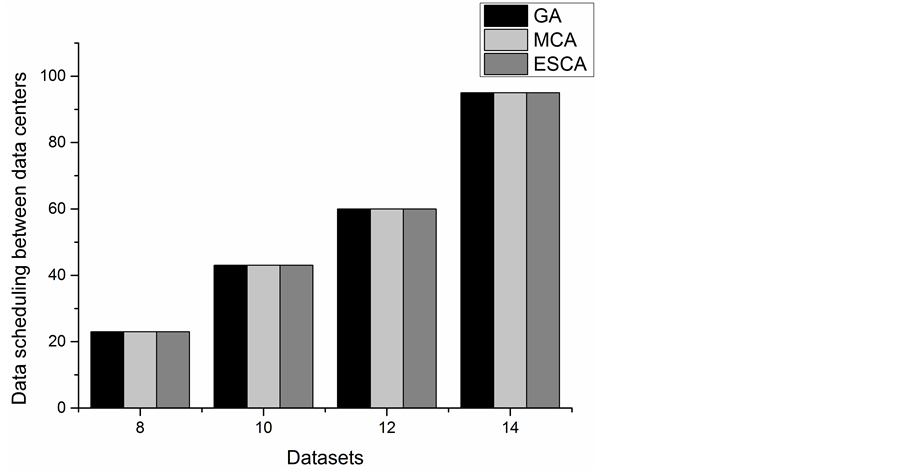
In this paper, genetic algorithm is applied to the placement of big data, and comprehensive performance test has been done. To verify the feasibility of genetic algorithm in data placement, we compared the data scheduling between data centers of solutions searched by genetic algorithm with exhaustive search algorithm when the number of datasets was small, the relationship between the minimum number of data scheduling of different number of datasets and the generation are represented by a line chart. We ran 10 test computations randomly for 400 times on 3 data centers and compared the data scheduling between data centers of solutions searched by different algorithms when the number of datasets changed. In genetic algorithm the size of initial population was 200, the maximum generations was set to 1000, and the crossover rate and the mutation rate were 0.5 and 0.05 respectively. The number of iterations of the Monte Carlo algorithm was 106.
The data scheduling between data centers of the three algorithms is shown in Figure 4. From Figure 4, we can find the results of the three algorithms are exactly the same in each case as the number of datasets changes. The results of exhaustive search algorithm are obtained by traversing, thus the corresponding results are the optimal data placement matrices, so using genetic algorithm and Monte Carlo algorithm can also find the optimal data placement matrices.
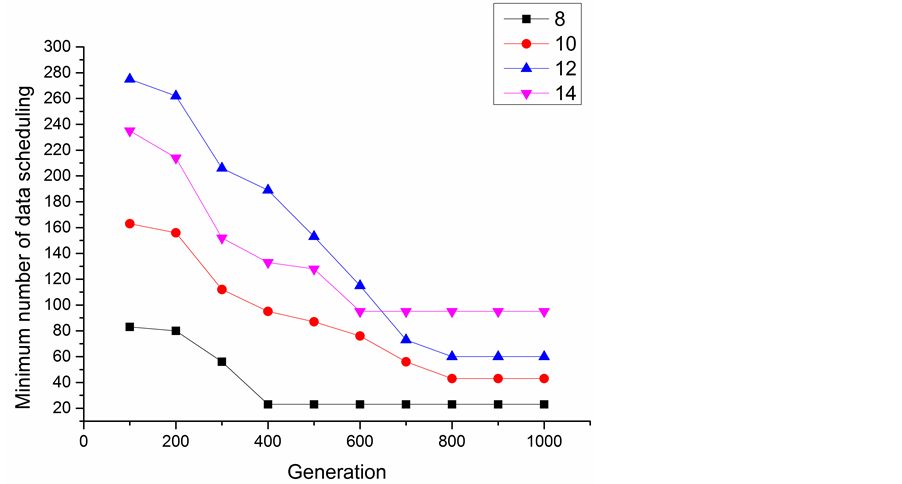
As Figure 5 schematically shows, with the increase of generation, the minimum number of data scheduling becomes smaller and smaller, optimization results get more and more close to the optimal solutions. When the number of datasets is 8, the convergence generation is around 400, the convergence generations of different number of datasets are different from each other.
Figure 4. Data scheduling between data centers with different number of datasets.
Figure 5. Minimum number of data scheduling in the evolution.
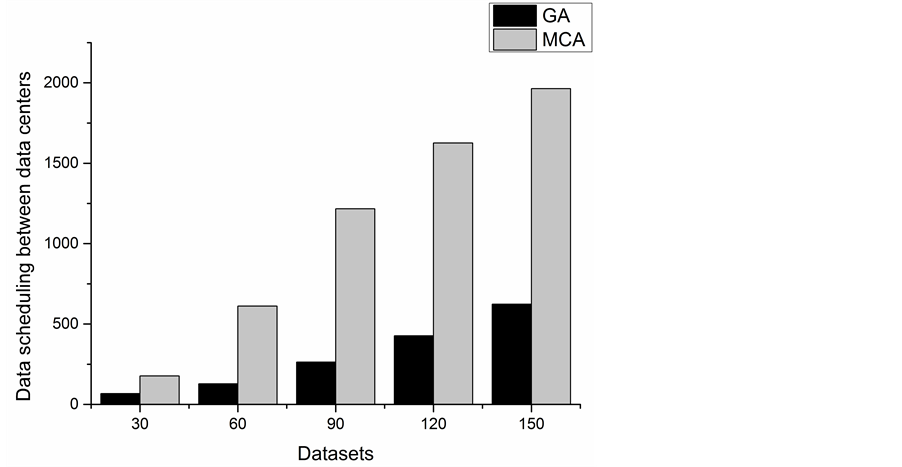
With the increase of the number of datasets, exhaustive search algorithm became infeasible because of the computation complexity. Then we compared the data scheduling between data centers of approximate optimal solutions searched by genetic algorithm with the results searched by Monte Carlo algorithm when the number of datasets was large, the optimization time of each algorithm were also compared. We ran 30 different test computations randomly for 2500 times on 5 data centers with different number of datasets, then we ran the test computations on different numbers of data centers when the number of datasets was 60. In genetic algorithm the size of initial population was 5000, the maximum generations was set to 2000, and the crossover rate and the mutation rate were 0.6 and 0.1 respectively. The number of iterations of the Monte Carlo algorithm was 109.
From the Figure 6 and Figure 7, we can see the increase of datasets or data centers leads to the growth of da-
Figure 6. Data scheduling between data centers with different number of datasets.
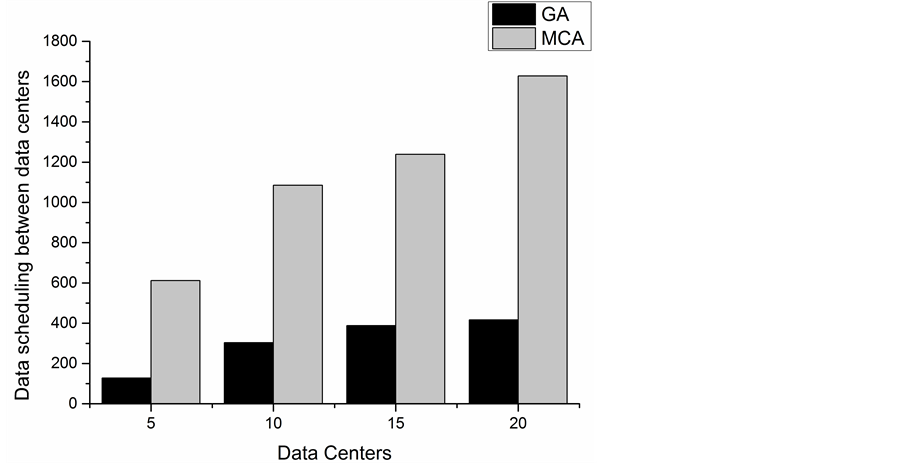
Figure 7. Data scheduling between data centers with diffferent number of data centers.
ta scheduling between data centers. By comparing the data, we find that the data scheduling between data centers of approximate optimal data placement matrices searched by genetic algorithm are always smaller than Monte Carlo algorithm in each case. So for data placement issue, in the case of large datasets, the search results of genetic algorithm are better than Monte Carloalgorithm.
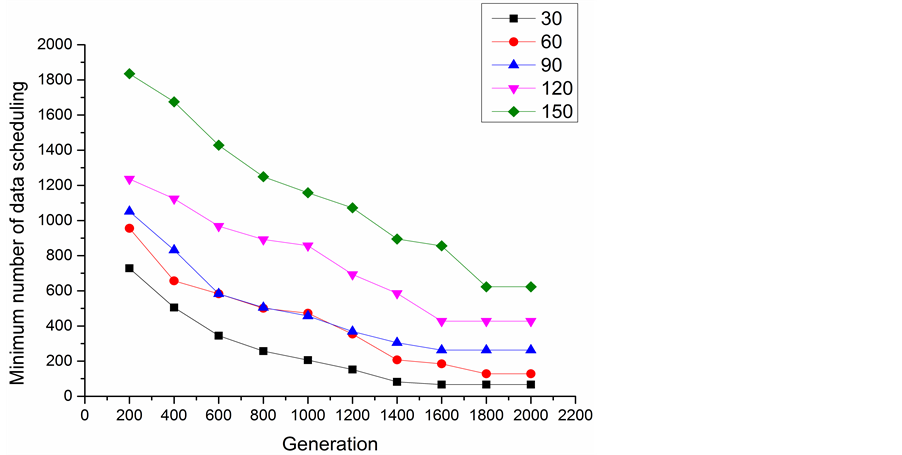
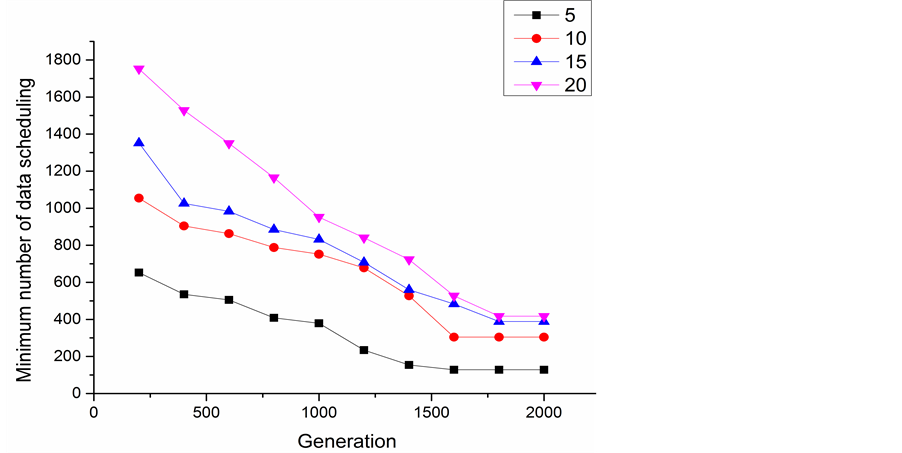
Figure 8 schematically shows the relationship between the minimum number of data scheduling of different number of datasets and the generation. In the experiment, the number of data center was fixed as 5. It appears that the convergence generations of different number of datasets are different from each other. Then the number of datasets was fixed as 60 and we ran 30 test computations randomly for 2500 times on different numbers of data centers, as shown in Figure 9. With the increase of generation, the minimum number of data scheduling becomes smaller, and optimization results get more close to the optimal solutions.
Figure 8. Minimum number of data scheduling of different number of datasets in the evolution.
Figure 9. Minimum number of data scheduling of different number of data centers in the evolution.
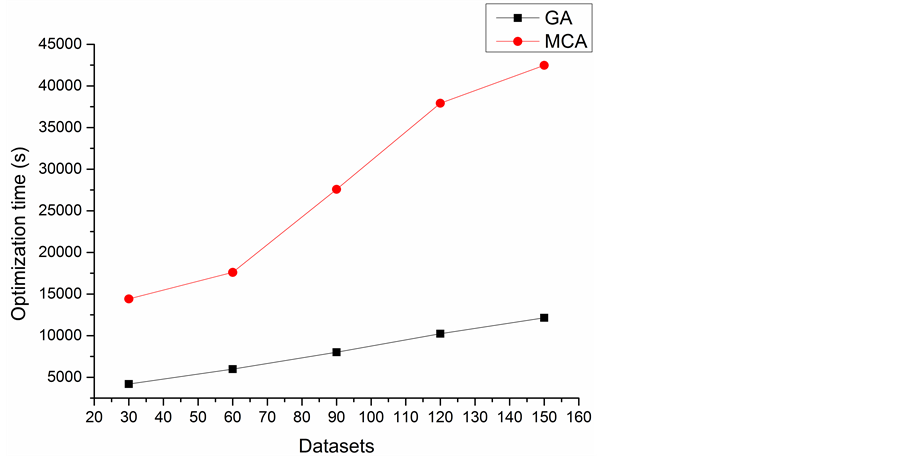
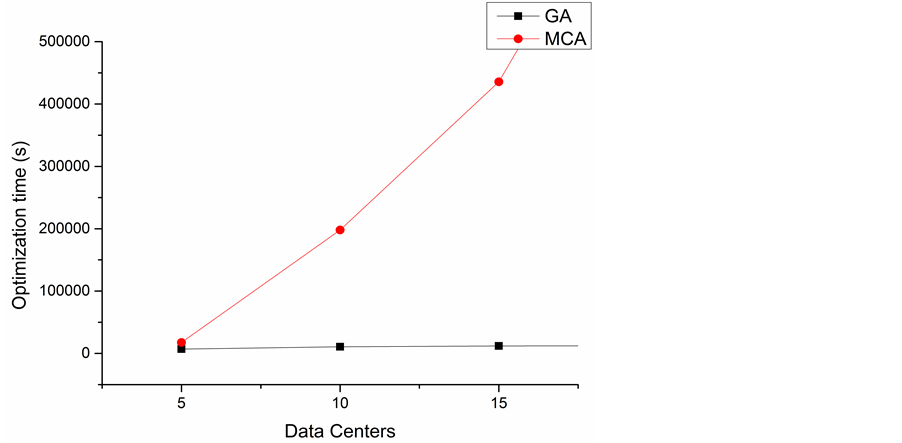
The optimization time of the two algorithms are showed in Figure 10 and Figure 11. We can find either the increase of datasets or the number of data centers would lead to the increase of the optimization time, and the growth rate of optimization time of Monte Carlo algorithm is much higher than genetic algorithm. It is time costly for Monte Carlo algorithm to find an approximate optimal data placement matrix when the number of datasets or data centers increase to a certain degree. In the case of large number of datasets, the characteristics of inherent parallelism and convergence of genetic algorithm made it possible to find a better solution within an acceptable time.
4. Summary and Future Work
In the environment of distributed cloud computing, placing data to the appropriate data center has become a
Figure 10. Optimization time of the two algorithms in different number of datasets.
Figure 11. Optimization time of the two algorithms in different number of data centers.
critical issue. Reasonable placement of datasets in data centers can minimize the number of data scheduling between the data centers. In this paper, a mathematical model is built to illustrate the relationship among datasets, data centers and computations. Three different algorithms are used to search the approximate optimal data placement matrices. By comparing genetic algorithm with exhaustive search algorithm and the Monte Carlo algorithm, we can work out the truth that under verifiable conditions, genetic algorithm can find the optimal data placement matrix; when the number of datasets is large enough, genetic algorithm can find an approximate optimal data placement matrix in a reasonable time, and the optimization result is better than Monte Carlo algorithm.
Currently, the focus of our research is to find an optimal data placement matrix, making the number of data scheduling between the data centers as small as possible. During the research, the impact of data access history and access heat on data placement are out of our consideration. The heat of the data and the execution frequency of computations are not constant over time, then data placement needs to update which increases the cost of data management for enterprise; this issue needs further study. In terms of genetic algorithms, the selection is an important operator. There are many selection methods, such as Roulette wheel selection method, league selection method, expectations selection method. In this paper we use Roulette wheel selection method. Different methods of genetic selection affect the performance of the algorithm which requires further study.
Acknowledgements
This paper is part of the research undertaken by Qiang Xu to obtain the Master’s Degree in communication and information system at Wuhan University, also as part of the complex application environments oriented theoretical study for data storage funded by the same university.
References
- Labrinidis, A. and Jagadish, H. (2012) Challenges and Opportunities with Big Data. Proceedings of the VLDB Endowment, 5, 2032-2033. http://dx.doi.org/10.14778/2367502.2367572
- (2008) Big Data. Nature, 455, 1-136.
- Manyika, J., Chui, M., Brown, B., et al. (2011) Big Data: The Next Frontier for Innovation, Competition, and Productivity. McKinsey Global Institute.
- Qiu, L., Padmanabhan, V.N. and Voelker, G.M. (2001) On the Placement of Web Server Replicas. Proceedings―IEEE INFOCOM, Anchorage, 22-26 April 2001, 1587-1596.
- Wolf, J. and Pattipati, K. (1990) A File Assignment Problem Model for Extended Local Area Network Environments. Proceedings of 10th International Conference on Distributed Computing Systems, Paris, 28 May-1 Jun 1990, 554-561.
- Scheuermann, P., Weikum, G. and Zabback, P. (1998) Data Partitioning and Load Balancing in Parallel Disk Systems. The VLDB Journal, 7, 48-66. http://dx.doi.org/10.1007/s007780050053
- Zhou, X. and Xu, C. (2002) Optimal Video Replication and Placement on a Cluster of Video-on-Demand Servers. Proceedings of International Conference on Parallel Processing (ICPP), 2002, 547-555. http://dx.doi.org/10.1109/ICPP.2002.1040912
- Doraimani, S. and Iamnitchi, A. (2008) File Grouping for Scientific Data Management: Lessons from Experimenting with Real Traces. Proceedings of the 17th International Symposium on High Performance Distributed Computing, ACM, Boston, 2008, 153-164.
- Fedak, G., He, H. and Cappello, F. (2008) BitDew. A Programmable Environment for Large-Scale Data Management and Distribution. ACM/IEEE Conference on Supercomputing, Austin, 15-21 November 2008, 1-12. http://dx.doi.org/10.1109/SC.2008.5213939
- Kosar, T. and Livny, M. (2005) A Framework for Reliable and Efficient Data Placement in Distributed Computing Systems. Journal of Parallel and Distributed Computing, 65, 1146-1157. http://dx.doi.org/10.1016/j.jpdc.2005.04.019
- Yuan, D., Yang, Y., Liu, X. and Chen, J.J. (2010) A Data Placement Strategy in Scientific Cloud Workflows. Future Generation Computer Systems, 26, 1200-1214. http://dx.doi.org/10.1016/j.future.2010.02.004
- Zheng, P., Cui, L.Z., Wang, H.Y. and Xu, M. (2010) A Data Placement Strategy for Data-Intensive Applications in Cloud. Chinese Journal of Computers, 33, 1472-1480. http://dx.doi.org/10.3724/SP.J.1016.2010.01472
- Nukarapu, D.T., Tang, B., Wang, L.Q. and Lu, S.Y. (2011) Data Replication in Data Intensive Scientific Applications with Performance Guarantee. IEEE Transactions on Parallel and Distributed Systems, 22, 1299-1306.
- Agrawal, D., Das, S. and El Abbadi, A. (2011) Big Data and Cloud Computing: Current State and Future Opportunities. Proceedings of the 14th International Conference on Extending Database Technology, Uppsala, 21-25 March 2011, 530-533.
- Goldberg, D.E. (1989) Genetic Algorithms in Search, Optimization and Machine Learning. Addison-Wesley Longman Publishing Co., Boston.
- Goldberg, D.E. (1989) Genetic Algorithms in Search, Optimization and Machine Learning. Addison-Wesley, Reading, MA.
- Grant, K. (1995) An Introduction to Genetic Algorithms. C/C++ Users Journal, 13, 45-58.
- Zhou, M. and Sun, S.D. (1999) Genetic Algorithms and Applications. National Defense Industry Press, Beijing.
- Mitchell, M. (1996) Introduction to Genetic Algorithm. MIT Press, Cambridge, MA.
- Pan, W., Diao, H.Z. and Jing, Y.W. (2006) A Improved Real Adaptive Genetic Algorithm. Control and Decision, 21, 792-795.
- Polgar, O., Fried, M., Lohner, T. and Barsony, I. (2000) Comparison of Algorithms Used for Evaluation of Ellipsometric Measurements Random Search, Genetic Algorithms, Simulated Annealing and Hill Climbing Graph-Searches. Surface Science, 457, 157-177. http://dx.doi.org/10.1016/S0039-6028(00)00352-6
- Tan, B.C., et al. (2008) A Kind of Improved Genetic Algorithms Based on Robot Path Planning Method. Journal of Xi’an University of Technology, 28, 456-459.
- Bäck, T. (1996) Evolutionary Algorithms in Theory and Practice. Oxford University Press, Oxford, 120.
- Liu, Z.G., Wang, J.H. and Di, Y.S. (2004) A Modified Genetic Simulated Annealing Algorithm and Its Application. China Journal of System Simulation, 16, 1099-1101.
- Deb, K., Pratap, A., Agarwal, S. and Meyarivan, T. (2002) A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6, 182-197.
- Wong, M. and Wong, T. (2009) Implementation of Parallel Genetic Algorithms on Graphics Processing Units. Intelligent and Evolutionary Systems, 187, 197-216.
NOTES
*Corresponding author.