International Journal of Intelligence Science
Vol.4 No.3(2014), Article
ID:48263,10
pages
DOI:10.4236/ijis.2014.43009
Adaptive Cascade Generalized Predictive Control
Tao Geng1, Jin Zhao2
1Academy of Physics and Electroics, Henan University, Kaifeng, China
2Academy of Control Science and Engineering, Huazhong University of Science and Technology (HUST), Wuhan, China
Email: gengtao@henu.edu.cn, jinzhao617@mail.hust.edu.cn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 May 2014; revised 25 June 2014; accepted 2 July 2014
ABSTRACT
Cascade control is one of the most popular structures for process control as it is a special architecture for dealing with disturbances. However, the drawbacks of cascade control are obvious that primary controller and secondary controller should be tuned together, which influences each other. In this paper, a new Adaptive Cascade Generalized Predictive Controller (ACGPC) is introduced. ACGPC is a method issued from GPC and the inner and outer controllers of a cascade system are replaced by one cascade generalized predictive controller, where both loops model are updated by Recursive Least Squares method. Compared with existing methods, the new method is simpler and yet more effective. It can be directly integrated into commercially available industrial auto-tuning systems. Some examples are given to illustrate the effectiveness and robustness of the proposed method.
Keywords:Adaptive Cascade Generalized Predictive Control, Model Identification, Cascade Control

1. Introduction
Cascade control is one of the most popular structures for process control as it is a special architecture for dealing with disturbances. It is widely used in practice, sometimes in a transparent way (embedded into the electronics of a servoactuator [1] , controlled power supply [2] , process control [3] etc.). The general block diagram of cascade control is shown in Figure 1. Cascade control refers to the design of a control loop for one primary variable by means of multiple sensors and/or actuators and, in its basic configuration; it consists of two cooperative SISO control loops with different time constants. The time constants in inner loop and outer loop are always different. And this difference allows for separate design using conventional techniques.

Figure 1. General block diagram of cascade control.
Previous researchers have proposed relay-based auto-tuning techniques to facilitate the design of cascade control systems. The methods proposed by Hang et al. [4] and Vivek and Chidambaram [5] need sequential application of the conventional relay-based auto-tuning approach, and are therefore still time consuming. The sequential tuning procedure has been improved so that only single relay experiment is required for auto-tuning [6] - [9] . However, an off-line or ad hoc experiment must be performed in these methods. For example, Leva and Donida [6] performed test with relay cascaded to an integrator, and Mehta and Majhi [8] restricted the secondary controller to controller during the relay test. Besides the relay-based method, Visioli and Piazzi [10] proposed an automatic tuning method consisting of an open-loop test for cascade control system. Veronesi and Visioli [11] recently proposed simultaneous closed-loop automatic tuning method for cascade controllers. Their method evaluates the set-point step response of cascade control system.
Whatever, based on the PID there are always two controllers needed to be configured. And obviously, the drawbacks of cascade control are obvious that primary controller and secondary controller should be tuned together, which influences each other. If there is not a substantial difference in time constants, although this strategy can still be pursued, the loop design cannot be made independently and based on SISO techniques. So tuning is not intuitive: centralized configurations might be preferable. CGPC [12] [13] is a method issued from GPC and the inner and outer controllers of a cascade system are replaced by one cascade generalized predictive controller. In this control paradigm, there is only one controller configured. If the models of inner process and out process were known, the controller can be auto-configured. This paper proposed an adaptive CGPC cascade controller shown in Figure 2. The both loops model are SISO. And the model can be identified by the classical method, respectively.
2. GPC with Constraints
GPC adapts the model so-called Controlled auto regressive integrated moving average (CARIMA) model [14] [15] .
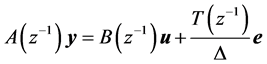 (1)
(1)
where, 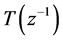 is the model of noise, but it is commonplace to treat
is the model of noise, but it is commonplace to treat 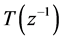 as a design parameter. Because it has direct effects on loop sensitivity and so better closed-loop performance will be got with a
as a design parameter. Because it has direct effects on loop sensitivity and so better closed-loop performance will be got with a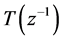 .
.
Then, a general form of future predictions is
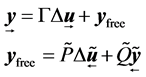 (2)
(2)
And the followed can be derived
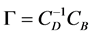 (3)
(3)
where, 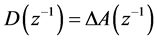
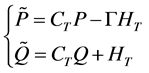 (4)
(4)
![]() is the toeplitz matrix of
is the toeplitz matrix of  and
and 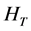 is the hankel matrix of
is the hankel matrix of 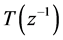 [16] . Constraints on process inputs and outputs make the controller and consequently the entire closed-loop, nonlinear.
[16] . Constraints on process inputs and outputs make the controller and consequently the entire closed-loop, nonlinear.
Use the cost function and optimization
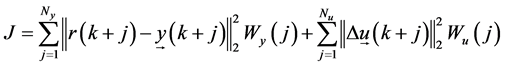 (5)
(5)
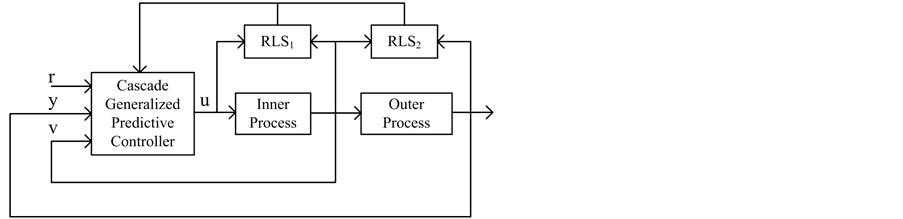
Figure 2. Proposed control paradigm of adaptive cascade control.
where, 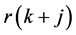 is j step ahead reference.
is j step ahead reference. 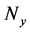 is receding horizon and
is receding horizon and 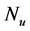 is control step.
is control step.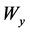 ,
, ![]() is the output and input weight factor. Described in matrix form, the GPC with constraints is converted to be the optimization problem which is
is the output and input weight factor. Described in matrix form, the GPC with constraints is converted to be the optimization problem which is
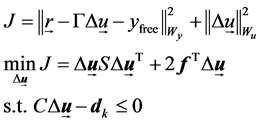 (6)
(6)
where, 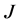 is subject of the following constraints. Where
is subject of the following constraints. Where 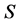 is positive definite and
is positive definite and![]() ,
, 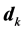 are time varying (dependent on the current state).
are time varying (dependent on the current state).
 (7)
(7)
The (6) is a standard quadratic programming with constraints. The constraints in GPC will be described as the following.
Ÿ The Control Law without Constrains Solve the 
The control law without constrains is derived as
 (8)
(8)
Ÿ Input move constraints
![]() is the lower bounds of input move constraints, and
is the lower bounds of input move constraints, and  is the upper bounds of input move constraints.
is the upper bounds of input move constraints.
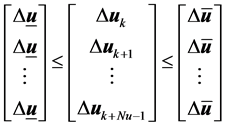
Which can be described in vector form as (9).
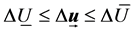 (9)
(9)
And satisfy the matrix inequality (10)
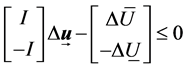 (10)
(10)
Ÿ Input constraints
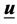 is the lower bounds of input constraints, and
is the lower bounds of input constraints, and 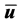 is the upper bounds of input constraints.
is the upper bounds of input constraints.
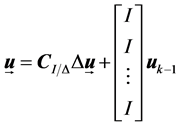
where,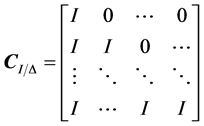 .
.
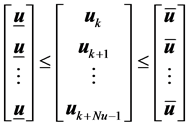
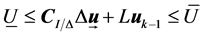 (11)
(11)
The corresponding linear inequalities are
Ÿ 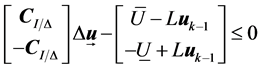
Ÿ Output constrains The output of plants always needs to be constrained in the bounds, as demand of process requirements. And they always are treated as soft constraints. 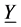 is the lower bounds of output constraints, and
is the lower bounds of output constraints, and 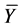 is the upper bounds of output constraints.
is the upper bounds of output constraints.
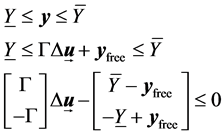 (12)
(12)
If all constraints are satisfied, the (6) can be described as
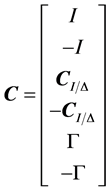 ,
,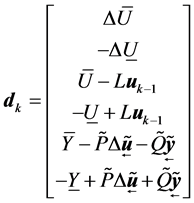 (13)
(13)
qpOASES (quadratic program Online Active SEt Strategy) is an open-source implementation of the recently proposed online active set strategy, which was inspired by important observations from the field of parametric quadratic programming [16] [17] . The standard form is
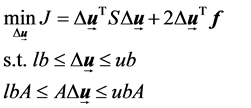
The (6) can be converted to be in the qpOASES form. And the followed can be derived from (9), (11), (12)
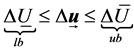
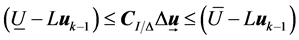
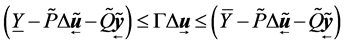
And we can get
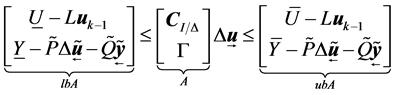
Algorithm 1-GPC with constraints 1) Firstly, we can identify the plant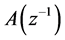 ,
, 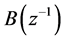 , and
, and 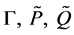 can be calculated from (3), (4), Specify the factor
can be calculated from (3), (4), Specify the factor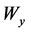 ,
, ![]() ,
, 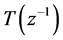 , receding horizon
, receding horizon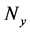 , control step
, control step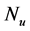 , bound of input
, bound of input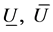 , bound of input rate
, bound of input rate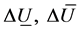 , bound of output
, bound of output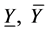 , calculate the
, calculate the![]() , initialize QProblem object (qpOASES).
, initialize QProblem object (qpOASES).
2) sample the output, update![]() .
.
3) update ![]() and QProblem object, return the optimization value
and QProblem object, return the optimization value![]() .
.
4) update![]() , output
, output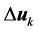 .
.
5) go to (2).
3. Cascaded Generalized Predictive Control
As shown in Figure 2, Inner process model is described as
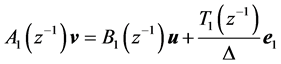 (14)
(14)
And outer process model is described as
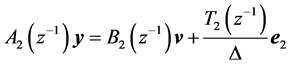 (15)
(15)
Similar to Formula (1) and (2), future predictions for Formula (14) is
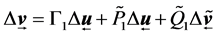 (16)
(16)
![]() means filter by
means filter by 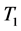
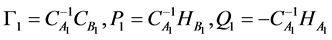
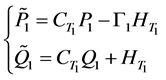
And the future predictions for Formula (15) is
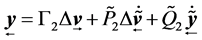 (17)
(17)
![]() means filter by
means filter by 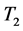
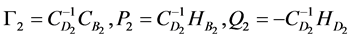
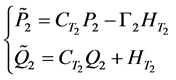
By substitution of Formula (16) into Formula (17)
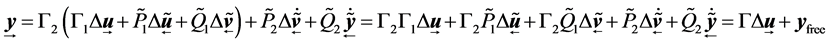
where, 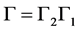 ,
, 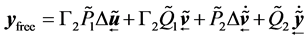
The control law without constrains corresponds with (8).
The control law with constrains for intermediate output
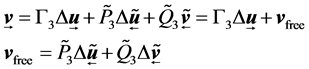 (18)
(18)
![]() means filter by
means filter by 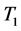
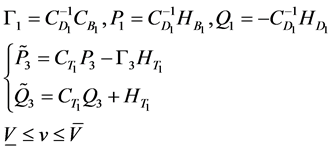 (19)
(19)
![]() is the lower bounds of intermediate output v constraints, and
is the lower bounds of intermediate output v constraints, and ![]() is the upper bounds. By substitution of Formula (18) into Formula (19)
is the upper bounds. By substitution of Formula (18) into Formula (19)
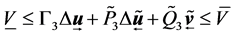
The corresponding linear inequalities are:
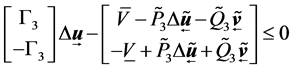
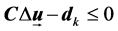
where,
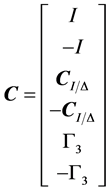 ,
,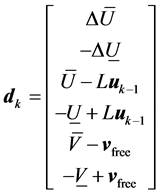
The control law with constrains is converted to be standard quadratic programming with constraints problem and can be solved by Algorithm 1.
4. Classical RLS Method
The SISO system can be identified by classical RLS method, which is described as followed.
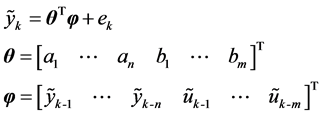 (20)
(20)
 means filter by
means filter by  in Equation (1). where
in Equation (1). where  is a vector of adjustable model parameters and
is a vector of adjustable model parameters and 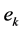 is the corresponding error at time
is the corresponding error at time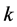 . The aim is to select
. The aim is to select  so that overall modeling error is minimized. The classical recursive least square algorithm is
so that overall modeling error is minimized. The classical recursive least square algorithm is
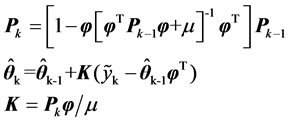 (21)
(21)
In the RLS algorithm, the 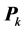 update equation Equation (21) is very sensitive to the truncation errors and there is no guarantee that
update equation Equation (21) is very sensitive to the truncation errors and there is no guarantee that 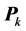 will always be positive and symmetric defined. The parameter identified by RLS will have biases from the true parameters, the stability and robustness of the algorithm is very poor. And then
will always be positive and symmetric defined. The parameter identified by RLS will have biases from the true parameters, the stability and robustness of the algorithm is very poor. And then 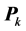 is revised as
is revised as
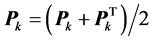
5. Verification on Proposed Scheme
Two examples are presented here to illustrate the effectiveness of the proposed tuning method for cascade control systems shown in Figure 2. The parameters of the ACGPC are in the Table1
In simulation, there is an identification process at first 100 s. Both inner and an outer model are identified by the classical RLS, respectively. The final value of model identified by the RLS is shown in the Table 2 and Table 3, respectively. And the Figures 3-6 show model parameters estimated by RLS. There is rarely fluctuation in convergence of parameter estimated. Based on the model, the CGPC is applied to control the cascade system. The outer process outputs (primary outputs) of the control loops are presented in Figures 5-8. The figure clearly shows the CGPC have excellent transient performance. This implies that all the good properties of the cascade control are kept in the ACGPC. This behavior is specific to the cascade structures. And the ACGPC can autotune the CGPC.
Table 2. Identification result of RLS for the real model.
Table 3. Identification result of RLS for the real model.
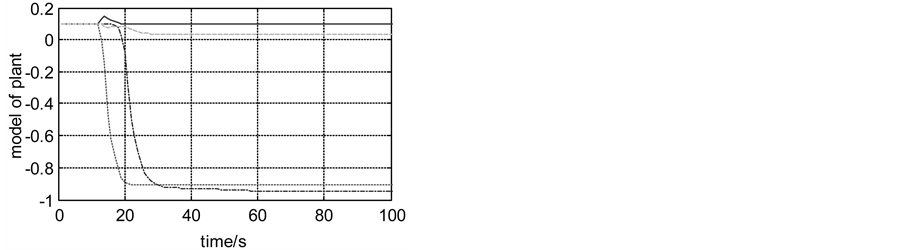
Figure 3. Identification result of RLS for the real model 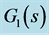 and
and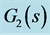 .
.
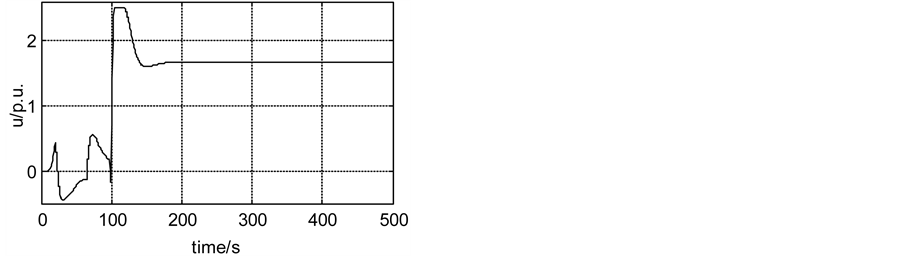
Figure 4. The control signals with and with control input constraints.
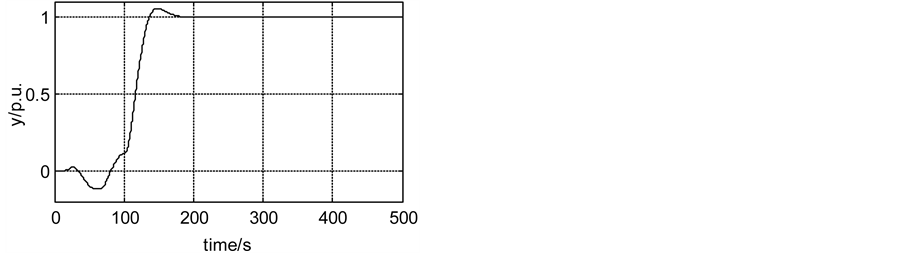
Figure 5. The tracking and regulation performance of the CGPC.
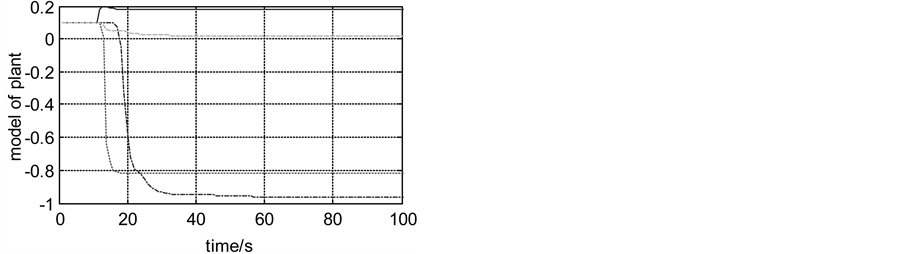
Figure 6. Regulation performance of the CGPC under inner disturbance disturbance which zoomed in Figure 5.

Figure 7. The control signals with and with control input constraints.
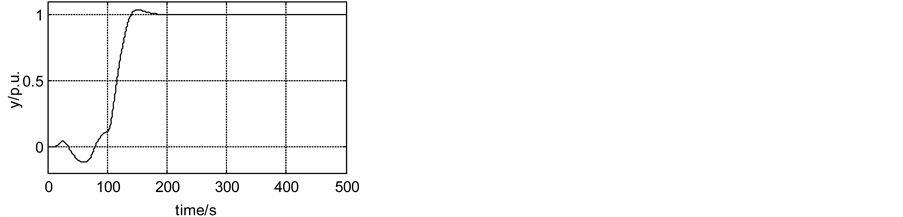
Figure 8. The control signals with and with control input constraints.
Example 1
The inner process is:
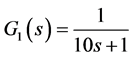
The outer process is:
• 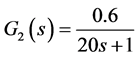
Example 2
The inner process is:
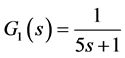
The outer process is:
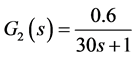
6. Conclusion
This paper developed an ACGPC method for the cascade control system, which gives the possibility to identify and control some different variables together. Both inner loop and outer loop process model, parameters can be identified using classical RLS method. Consequently, well-identified model based on CGPC can be applied to cascade control system. Finally, two examples were given to show the effectiveness of the proposed method. The method is very straightforward and has been integrated into an existing auto-tuning system. It is now being tested in an electrical drives system and the field results will be reported soon.
Acknowledgements
This work was supported by Henan University Science Foundation 2013YBZR013 and National Natural Science Foundation of China with grant number 61273174.
References
- Pisano, A., Davila, A., Fridman, L., et al. (2008) Cascade Control of PM DC Drives via Second-Order Sliding-Mode Technique. IEEE Transactions on Industrial Electronics, 55, 3846-3854.http://dx.doi.org/10.1109/TIE.2008.2002715
- Tsang, K.M. and Chan, W.L. (2008) Non-Linear Cascade Control of DC/DC Buck Converter. Electric Power Components and Systems, 36, 977-989. http://dx.doi.org/10.1080/15325000801960937
- Wolff Erik, A. and Skogestad, S. (1996) Temperature Cascade Control of Distillation Columns. Industrial & Engineering Chemistry Research, 35, 475-484.
- Hang, C.C., Loh, A.P. and Vasnani, V.U. (1994) Relay Feedback Auto-Tuning of Cascade Controllers. IEEE Transactions on Control Systems Technology, 2, 42-45. http://dx.doi.org/10.1109/87.273109
- Vivek, S. and Chidambaram, M. (2004) Cascade Controller Tuning by Relay Auto Tune Method. Journal of the Indian Institute of Science, 84, 89-97.
- Leva, A. and Donida, F.F. (2009) Autotuning in Cascaded Systems Based on a Single Relay Experiment. Journal of Process Control, 19, 896-905. http://dx.doi.org/10.1016/j.jprocont.2008.11.013
- Song, S., Cai, W. and Wang, Y.G. (2003) Auto-Tuning of Cascade Control Systems. ISA Transactions, 42, 62-72.http://dx.doi.org/10.1016/S0019-0578(07)60114-1
- Tan, K.K., Lee, T.H. and Ferdous, R. (2000) Simultaneous Online Automatic Tuning of Cascade Control for Open Loop Stable Processes. ISA Transactions, 39, 233-242. http://dx.doi.org/10.1016/S0019-0578(00)00006-9
- Visioli, A. and Piazzi, A. (2006) An Automatic Tuning Method for Cascade Control Systems. Proceedings of the IEEE International Conference on Control Applications, Munich, July 2006, 2968-2973.
- Veronesi, M. and Visioli, A. (2011) Simultaneous Closed-Loop Automatic Tuning Method for Cascade Controllers. Control Theory and Applications, 5, 263-270.
- Benyó, I. (2006) Cascade Generalized Predictive Control—Applications in Power Plant Control. University of Oulu, Oulu.
- Benyó, I. (2007) Cascade Generalized Predictive Controller: Two in One. International Journal of Control, 79, 866-876.
- Clarke, D.W., Mohtadi, C. and Tuffs, P.S. (1987) Generalized Predictive Control—Part II. Extensions and Interpretations. Automatica, 23, 149-160. http://dx.doi.org/10.1016/0005-1098(87)90088-4
- Clarke, D.W., Mohtadi, C. and Tuffs, P.S. (1987) Generalized Predictive Control—Part I. The Basic Algorithm. Automatica, 23, 137-148. http://dx.doi.org/10.1016/0005-1098(87)90087-2
- Rossiter, J.A. (2003) Model-Based Predictive Control-A Practical Approach. CRC Press, Washington DC, 54-58.
- Ferreau, H.J. (2009) qpOASES (Quadratic Program Online Active SEt Strategy) Version 2.0. http://www.qpoases.org/
- Ferreau, H.J., Bock, H.G. and Diehl, M. (2006) An Online Active Set Strategy for Fast Parametric Quadratic Programming in MPC Applications. Proceedings of the IFAC Workshop on Nonlinear Model Predictive Control for Fast Systems, Grenoble, 2006, 21-30.


