International Journal of Intelligence Science
Vol.2 No.2(2012), Article ID:18668,8 pages DOI:10.4236/ijis.2012.22005
Multi-Scale Object Perception with Embedding Textural Space
Department of Computer and Information, Hefei University of Technology, Hefei, China
Email: wu_kewei1984@163.com
Received January 10, 2012; revised February 21, 2012; accepted February 28, 2012
Keywords: Object Perception; Scale Space; Textural Manifold; Quad-Tree Structure; Nonparametric Estimation
ABSTRACT
This paper mainly focuses on the issues about generic multi-scale object perception for detection or recognition. A novel computational model in visually-feature space is presented for scene & object representation to purse the underlying textural manifold statistically in nonparametric manner. The associative method approximately makes perceptual hierarchy in human-vision biologically coherency in specific quad-tree-pyramid structure, and the appropriate scale-value of different objects can automatically be selected by evaluating from well-defined scale function without any priori knowledge. The sufficient experiments truly demonstrate the effectiveness of scale determination in textural manifold with object localization rapidly.
1. Introduction
Scene perception has been drawn more attentions for global scene understanding in recent years. There have been several considerable topics about rapid acquisition of scene gist; scene recognition; spatial layout and spatial scale [1]; distance perception in scenes [2]; updating of scene views over time; visual search for meaningful objects in scenes [3]; scene context effects on object perception [4]; scene representation in memory [5]; the allocation of attention including eye fixations during scene viewing; and the neural implementation of these representations and processes in the brain, that all of them stand for focusing research direction in computer vision. Generally, scale problem of object in scenes is the basis of highly-complex scene perception, that is, how to computationally approximate the object size close to the groundtruth, and additionally, it is magnificent to filter some trivial noise for more object-level cue concentrations in further specific vision tasks like object recognition, object localization or visual attention.
In absence of a priori, like spatial configuration or scale information, about unseen scene, it is usually confused in perception by seemingly invalid interpretation in similar settings as Biederman’s violations [6]. Recently, characteristics of local scene have been studied to encourage more frequently appearance on reusable structured-element combinations owing to part-based models for specific-class categorization [7]. However, consistency of local appearance varies dramatically in reality and should be maintained in different-size scale from individual pixels to one entire image in human visual system. The scale space description in Lazebnik and Schmid [8] prefers to hierarchical structure for computational convenience and more nature evidences come from results in biological [9] and cognitive view [10]. The spatial pyramid framework can offers insight into the successful representation performance with more popularities as Torralba’s “gist” [11] and Lowe’s SIFT [12] descriptors currently. From mostly empirical segmentation [13], finer-scale splitting leads to more accurate details and vice visa. Therefore, local appearance and structure in scale-space retain not only additional assumptions but also soft constraints to eliminate large-scale impossible configurations for improvement in scene understanding.
The versatile appearance, location, scale, depth and other perceptible properties enforcing consistency in local scene tend to be requirement of object-level understanding. N. Bianchi, etc. studied the mechanisms related to color perception in clutter settings and encapsulated the wrapped color categories using labeling [14]. Kang, Yousun, etc. discussed a method for depth perception from a 2D natural scene using scale variation of patterns. As the surface from a 2D scene farther away from observers, the texture appearances from eyes might tune to be finer and smoother [2]. A. H. Assadi verified the advantages of Gestalt theory in natural surfaces as a concrete computational approach to simulate or recreate images whose geometric invariance and quantities might be perceived and estimated by an observer [15].
Although overall methods provide an approximate estimation of above properties, it contains relatively sophisticated and complicated algorithms with loss of generality to some extents and the metric distance in Euclidean space lead to feature fragments. Zhu etc. applies entropy statistics to study a perceptual scale space by constructing a so-called sketch pyramid which augments the common-used Gaussian and Laplacian pyramid in image scale space theory [1]. The complete manifold pursues to ensemble these scattered pieces to overcome the density estimation inconsistency in original feature space [16] and project the high-dimensional data point onto parametric surface to keep intra-class similarity and betweenclass distinctness in both explicit and implicit case, with flexible transformation with each other [17].
The current object scale perception mostly has a biological psychology research foundation, and how to achieve an effective computational model appears well-promising. This paper aims at local scene perception, puts forward a non-parametric estimation method in texture feature space. The salient image patch in a pyramid space is introduced with informative statistics. Perception rate as evaluation function is used to calculate the best object scale in natural scene by the different generative masks.
2. Object Representations in Texture Feature Space
Based on the histogram of original gray information, entropy as one dimension feature can rapidly effectively describe image patch texture information, but it also to be confronted the inefficient multi-categories recognition task. To achieve the low dimension smooth texture description, frequency-domain analysis can give proper distribution statistic information. Gist Feature is promote by a group of Gabor filters, extracting frequency responsibility of different direction and scale edge, to obtain better texture recognition accuracy by its mean value of partitioned organization.
The texture appearance instinctively preserves the repetitive local structure with some particular frequencies as regular homogeneity in intermediate scale which is not dependent on color or brightness but contrast and finer scale will lead to disappearance of this phenomenon. The advanced important characteristics as roughness, openness, perspective induced by some multiple combinations with basic elements as orientation, magnitude or frequency in statistical manner over hierarchical layers. Moreover, it is beneficial to capture multiple scale, translation, viewpoint and illumination invariance, especially the common modality of category among most-varying appearances.
Spatial-frequency transformation is the widely-applied technique in image texture analysis. After this, in finite 2D-planar texture, periodic and symmetry features will be easily expressed as convolution with several selective filter banks originally from fruits in biological vision. Therefore, each image can be decomposed as a set of textons in multiple frequencies and directions that will be valuable for our further scale discussion.
Gist features [18,19] use multi-dimensional, multiscale Gabor filters to represent the diverse responses in scene. As the convolution with Gabor filter can be thought as a wavelet transformation, therefore, for images f(x, y), with original coordinate (x, y) in pixels, the two-dimensional output is as follows.
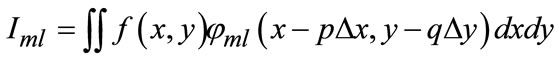 (1)
(1)
where 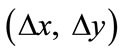 is one particular spatial sampling interval, in special case
is one particular spatial sampling interval, in special case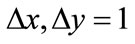 . Let p, q denote the position of image pixels and m, l respectively define the M direction and L scale mother wavelets, indexed by m = 0, …, M – 1 and l = 0, …, L – 1. Corresponding response
. Let p, q denote the position of image pixels and m, l respectively define the M direction and L scale mother wavelets, indexed by m = 0, …, M – 1 and l = 0, …, L – 1. Corresponding response 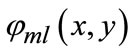 can be generated by template convolution with expression as two-dimensional separable Gaussian distribution omitting suffix,
can be generated by template convolution with expression as two-dimensional separable Gaussian distribution omitting suffix,
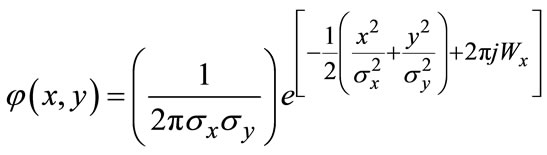 (2)
(2)
here, the value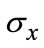 ,
, 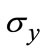 can be associated with direction and scale indexes m, l, W defines the frequency bandwidth in filter. In light of materials the neural and neuron system, set W = 0.5 with equal contribution from two directions.
can be associated with direction and scale indexes m, l, W defines the frequency bandwidth in filter. In light of materials the neural and neuron system, set W = 0.5 with equal contribution from two directions.
In this paper, the Gabor-like filter sets with 4-orientation and 8-direction, are selected to achieve 32 responses in image totally. In each filter channel, the normalization is performed by image block mean value. Therefore, any image can be represented as one 32-dimensional texture vector in row-or-column first order.
Texture decision function is design for different sample image patches, and its complexity is determined by categories variation and model parameter selected. Histogram information sampled from one image or few image, can leave out some representative object. So, for providing a precise category center and similarity threshold, to define its covering surface in feature data surface, a large content training sample must be included for effective test sample recognition.
From above representation, each image might be projected into subspace with fixed dimension as one point, in non-parametric manner, the samples from same category ensemble a texture hyper-sphere for density estimation.
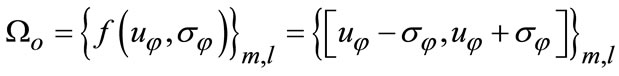 (3)
(3)
where 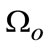 is feature domain,
is feature domain, 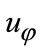 is feature mean value.
is feature mean value.  is feature standard deviation.
is feature standard deviation.
In order to satisfy the statistical sufficient condition, the lower boundary of number of samples should be determined (usually take 50) to formulate effective texture domain 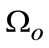 for smoothness, conversely, less number of the texture membership cause large variance inducing many sharp peaks as original normal distributions with perturbed noises, so in this case, we could resort to estimator of
for smoothness, conversely, less number of the texture membership cause large variance inducing many sharp peaks as original normal distributions with perturbed noises, so in this case, we could resort to estimator of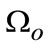 , that is
, that is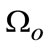 .
.
This paper proposes one effective representation about object texture in data distribution and non-parametric density estimation can capture the embedding structure. However, one challenge perception as scale heavily blocks the object saliency, so we sequentially present one method for automatic scale approximation in hierarchical quadpyramid.
3. Hierarchical Perceptions in Scale Space Prepare
3.1. Quad-Tree Partition
Traditional object detection task is mainly focus on object existence judgment by image scanning of object template. Known from detection, this paper research is the parametric estimation procedure with a special evaluation criterion. Intercrossed with the object detection, scale perception is to verify the scale information to give out a proper size description in human vision.
More and more evidences have been shown that the entire workflows about human visual perception exhibit coarse-to-fine hierarchical characteristics [20]. Being slightly different from hierarchy defined in [21], we simply apply quad-tree structure with fixed partition points shown in Figure 1, due to the efficiency requirements when determining size of sliding-window in object detection [22] and image can be defined as a sequence in depth 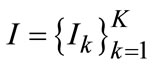 with subscript matrix R. K denotes perception scale as depth detail parameter for human attention and plays a central role in our method, then images are sequentially further partitioned into several planar sets in each scale, that is
with subscript matrix R. K denotes perception scale as depth detail parameter for human attention and plays a central role in our method, then images are sequentially further partitioned into several planar sets in each scale, that is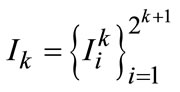 . Similarly,
. Similarly,
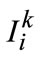 is expressed as sub-image content with subscript region
is expressed as sub-image content with subscript region 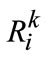 from image I as in Equation (4).
from image I as in Equation (4).
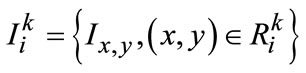 (4)
(4)
In more details, 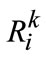 is the regional subscript set of the i-th patch of the k-th layer in quad-tree, (X, Y) is the size of image.
is the regional subscript set of the i-th patch of the k-th layer in quad-tree, (X, Y) is the size of image.
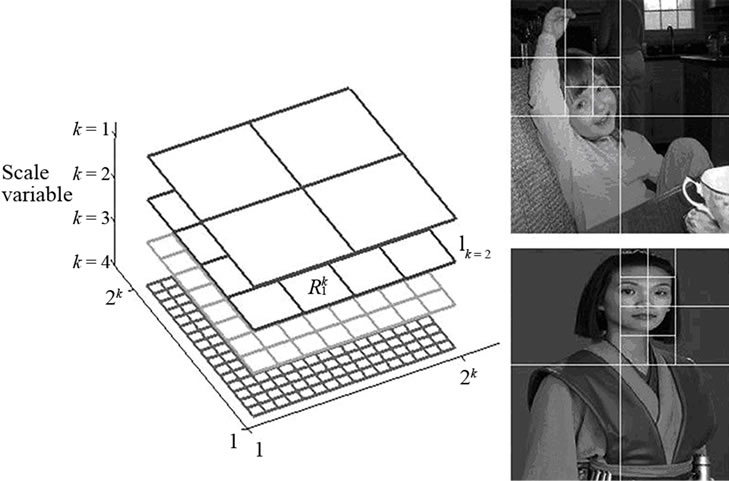
Figure 1. Quad-tree pyramid structure in scale space.
Each patch in quad-tree pyramid has exclusive index, and it is easy for search and location. Quad-tree pyramid confused the pyramid and grid partition strategy can embody not only image detail from coarse to fine, but also image layout distribution. Another characteristic of quadtree pyramid is image division not cover, patches analysis in same layer without redundancy, and it is easy to compress coarse to fine information in one image like human vision.
As above definition, scale-space has been naturally discretized into different-size patches and searching complexity reduces from O(m, n) as traditional one to 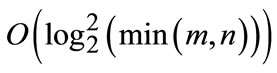 at the cost of fixed-grid size assumption. We could not mentioned its limitation just for the situation that we purely want to achieve approximation of object size rather than the refined accurate location, so in many instances, the objects in scene should not be entirely maintained in any one partition, but it does not lead to severe deterioration in our algorithm.
at the cost of fixed-grid size assumption. We could not mentioned its limitation just for the situation that we purely want to achieve approximation of object size rather than the refined accurate location, so in many instances, the objects in scene should not be entirely maintained in any one partition, but it does not lead to severe deterioration in our algorithm.
On the basis of scale representation, the first considerable issue is to separate object as foreground from clutter scene with texture appearance in scale-space. Denote  as foreground regions and
as foreground regions and 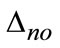 as background ones, and in multiple scale-space, we can further split
as background ones, and in multiple scale-space, we can further split 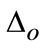 into
into  as:
as:
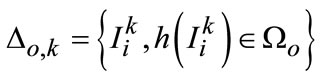 (5)
(5)
where 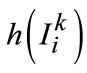 is the image patch
is the image patch 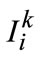 histogram of different feature descriptor and
histogram of different feature descriptor and 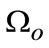 is the category subspace. Instinctively, binary segmentation commonly treats them as one mask generations Mk, that is “1” as object and “0” as non-object in Equation (6).
is the category subspace. Instinctively, binary segmentation commonly treats them as one mask generations Mk, that is “1” as object and “0” as non-object in Equation (6).
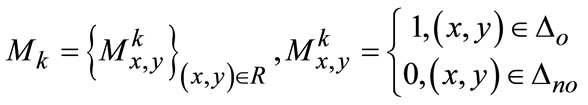 (6)
(6)
Formula (7) ![]() can be derived in scale-space that
can be derived in scale-space that
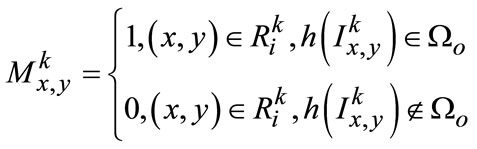 (7)
(7)
Actually, these perceptual masks can be directly obtained in each layer of quad-tree that is tightly related to the scale perception, so the approximation about object size should be converted into evaluation of binary mask Mk for largest response with particular depth k, often called as object perception scale. We can easily make estimation from precision ratio and recall rate as follows respectively in Equation (8) and Equation (9):
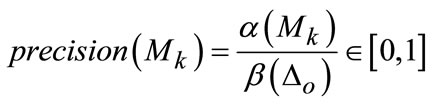 (8)
(8)
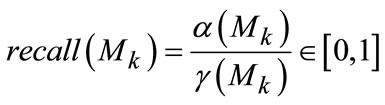 (9)
(9)
Both values from above fall into regions between 0 and 1, where  is the number of detected pixels with object truth,
is the number of detected pixels with object truth, 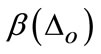 is amount of total pixels with object labeling and
is amount of total pixels with object labeling and 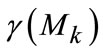 aggregates the pixel members in current scale space, triple of them can also be extended by Equation (10)-(12), considering the binary mask,
aggregates the pixel members in current scale space, triple of them can also be extended by Equation (10)-(12), considering the binary mask,
 (10)
(10)
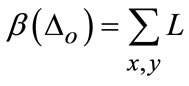 (11)
(11)
 (12)
(12)
where L shows the groundtruth mask, 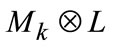 denotes the intersection set between Mk and L.
denotes the intersection set between Mk and L.
As for precision rate precision(Mk), the larger value indicates that the object can be detected in higher probability to drop out many uninformative regions. Considering the recall rate recall(Mk), the larger one often lead to the higher probability that the object occupies the full instance set. Generally, these two criterions can be hardly consistent encountering underand over-perception. The former case usually causes higher recall but lower precision value and contrary phenomenon appears in latter case, so the trade-off between precision and accuracy should be well considered by designing proper estimator defined in Equation (13)
 (13)
(13)
The numerator in fraction coincides with correct-labeling pixels in Equation (8) and Equation (9) and the denominator compromises two cases with normalization for convergence guarantee in  with the value between 0 and 1. At this point, scale perception problem can be formulated as the optimization over scale parameter k in evaluation function
with the value between 0 and 1. At this point, scale perception problem can be formulated as the optimization over scale parameter k in evaluation function
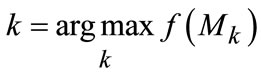 (14)
(14)
3.2. Single-Object Scale Perception
For labeling images, the scale perception computationally degenerates to the some qualitative measure over a set of marked pixels from given image blocks and therefore we separate particular marked masks into different non-intersect subsets in scale space
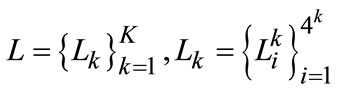 (15)
(15)
It can be viewed as to be perceptible in particular image block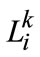 , where the number of marked pixels exceeds to a certain threshold and the ratio of the truthmarker over all pixels is defined to measure quantities of labeling in image.
, where the number of marked pixels exceeds to a certain threshold and the ratio of the truthmarker over all pixels is defined to measure quantities of labeling in image.
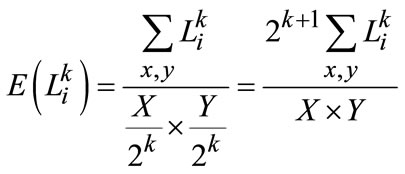 (16)
(16)
According to the Equation (7), mask can be transformed into binary codes in term of particular measurement above,
 (17)
(17)
Similarly as in Equation (14), marking scale can be obtained corresponding to the largest value of evaluation function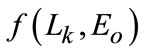 ,
,
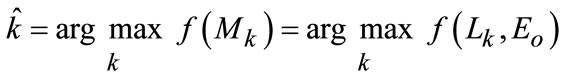 (18)
(18)
In training image set, each one image with one scalar parameter, scale vector of multiple masks can be denoted as 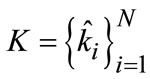 and priori as
and priori as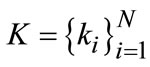 , the covariance of these two vectors can be limited to guarantee the scale consistency. The parameter estimation can be iteratively performed in different 50 training sets to take
, the covariance of these two vectors can be limited to guarantee the scale consistency. The parameter estimation can be iteratively performed in different 50 training sets to take 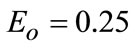 according to the formula (19) empirically.
according to the formula (19) empirically.
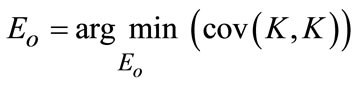 (19)
(19)
A single marked-object image with labeling L can be decomposed into many blocks with fixed-size 16-by-16 and 256-gray-level value in 4-layer pyramid structure.
In Table 1: SV means Scale variables, ETD means Estimation texture domain, STD means Statistical Texture domain.
Figure 2(a)-(d) show the perception results when the scale variable is set to 1, 2, 3, 4 respectively in texture feature space , where the distinct perceptible regions can be highlighted in bright style and shading ones can be automatically regard as clutter background. As quantities measurement of perception rate in Equation (13) achieve well-behavior for trade-off between overand under-perception, this can serve as criterion for scale parameter in single object. Table 1 shows the specific real value of scale estimation and statistical computation for each detecting mask in Figure 2. The scale in second row is taken for its largest value 0.55 in perception rate in statistical way.
, where the distinct perceptible regions can be highlighted in bright style and shading ones can be automatically regard as clutter background. As quantities measurement of perception rate in Equation (13) achieve well-behavior for trade-off between overand under-perception, this can serve as criterion for scale parameter in single object. Table 1 shows the specific real value of scale estimation and statistical computation for each detecting mask in Figure 2. The scale in second row is taken for its largest value 0.55 in perception rate in statistical way.
Large-scale samples for texture computation in statistical view can capture a better representation in object manifold, comparing to estimated texture scale based on single marked image. Therefore, the local scene perception problem is transformed into the constrained evaluation preventing from improper perception in object detected patches, so as to achieve an object scale perception procedure closest to the effects in human visual brain.
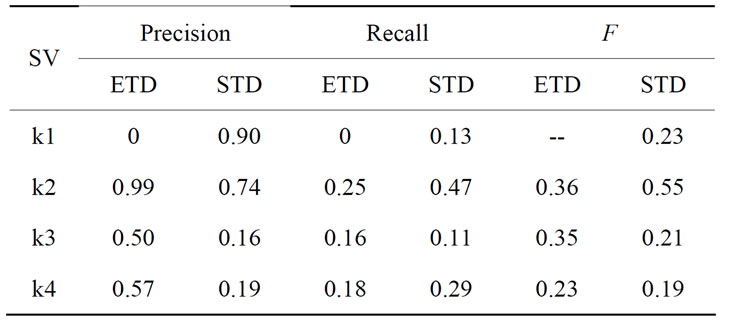
Table 1. Scale perception evaluation in single-object containing image.
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 2. Scale perception of single object image in different values from coarse-to-fine hierarchies as left-to-right shown.
3.3. Multiple-Instance Scale Perception
In this section, we will extend our method to deal with more complex cases that to automatically approximate the multiple object location with estimated scale parameter. The workflow of our scale perception algorithm is listed as follows:
Step 1. Select training set in each category (sample form 50 region-labeled images), calculate texture features statistically in space  for object verification using Equation (3);
for object verification using Equation (3);
Step 2. Construct test image scale pyramid 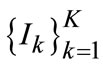
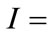 based on the quad-tree on test image I;
based on the quad-tree on test image I;
Step 3. Estimate objects perception mask 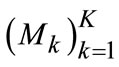 with given object in each scale according to Equation (7);
with given object in each scale according to Equation (7);
Step 4. Compute recall and precision of the image mask for evaluations as in Equation (8) and Equation (9);
Step 5. Infer the perception rates 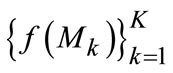 in various scales defined in Equation (13);
in various scales defined in Equation (13);
Step 6. Determine the best perception scale with Equation (14).
Experiment 1: In Caltech 256 [23] image dataset, three categories of different organizational structures as coffee mug in 41-th, computer-monitor in 46-th and people in 159-th are selected for multi-instance verification respecttively. We analysis perception rate of different scale and feature, compare 1-dimension entropy value to 32-dimension texture vector.
Figure 3 shows the accuracy rate of image object scale perception based on the perception evaluation, and respectively discussed performance efficiency in different feature spaces between the entropy domain [1] and texture domain. As ground-truth manual annotation with bounding box labeling object in each test image, we make a considerable comparison of our estimated scale to subjective scale with the parameter Eo = 0.25 in Equation (19). The accuracy rate of the scale perception in Figure 3. can reach to 81% accuracy for face category when scale is 1, and along with the detail segmentation, the accuracy decrease in small resolution. But our method can still achieve the suboptimal solution as 63% in case that scale is 4. Figure 3 verifies the scale perception method based on the texture domain feature space and spatial pyramid strategy, and has an extensive applicability to the multi-instance case.
Experiment 2: As scale perception is similar to object detection, different scale average accuracy can manifest the importance of object feature selection. The Pascal VOC [24] image dataset is also concentrated for its location prediction with bounding box and labeling of each object from twenty categories in each test image. The image sets are preprocessed by a random sampling image patches assembling the entire training set to learn the density distribution in statistical way as the parameters of mean and variance. Meanwhile, estimation process is independently executed in the quad-tree of test image itself.
Figure 4 shows the average scale accuracy in twenty categories, such as bicycle, bird, boat, bottle, bus, car, cat, chair, cow, dining table, dog, horse, motorbike, person, potted plant, sheep, sofa, train, TV/monitor. The average scale accuracy is about 52% at entropy domain and 56% at texture domain. There 13 categories can obtain proper scale estimation in texture domain, while 11 categories in entropy domain. The top three categories are aero-plane person and train with 83.8% 82.5% 76.2% in texture domain and 83.3% 78.3% 74.4% in entropy domain. Due to the complexity of object detection, a non-parametric method for the object scale perception in the quad-tree structure is comparably brief and effective.
The proposed method has some contribution to scale perception as follows. Firstly, Gist as a group of Gabor filters can give a simple effective texture descriptor, and its feature dimension can fit the model complexity. Secondly, quad-tree pyramid is easy to search and location like human vision and the scale perception mask can provide foreground analysis information.
4. Conclusion
This papers start from capturing the probability density in the object feature space, employing non-parametric estimation methods to determine the object scale perception and its computational model via texture domain. The texture-like feature computation and extraction is an effective way for representation of object surface perception; and perception rate can provide a reasonable evaluation based on strategy in the quad-tree spatial segmentation. But, in multi-class case, additional supervision classification methods should be required for further estimation of probability density to accomplish recognition and

Figure 3. accuracy rate with different scale of three selected categories in Caltech 256.
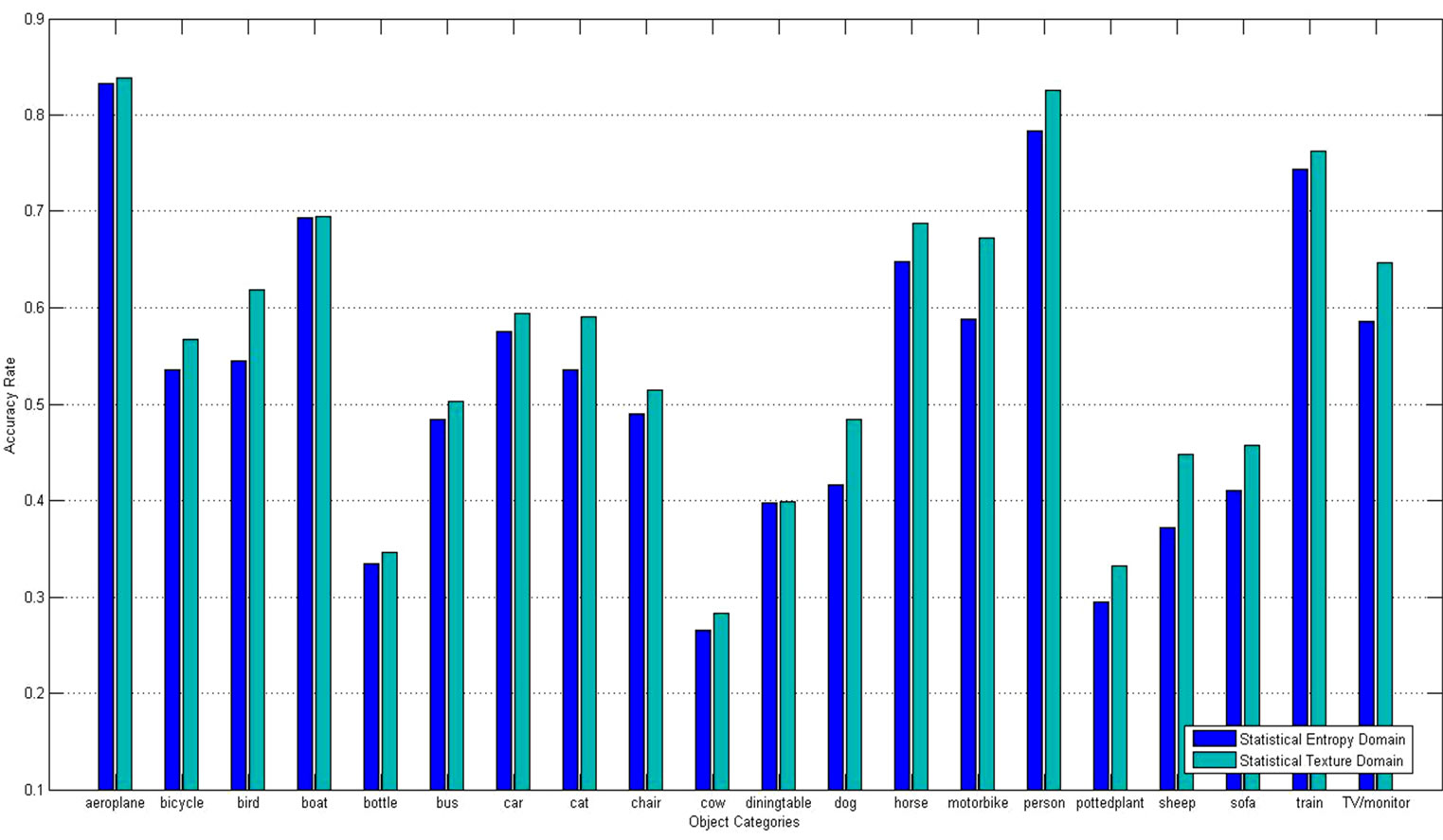
Figure 4. Accuracy rate of different categories in Pascal VOC.
detection tasks. Meanwhile, hierarchical quad-tree structure has a strong dependence on the position and orientation. Our method can confirm the best scale evaluations mainly for salience application rather accurate object localization. Therefore, a better alternative strategy of scale-space description should be further developed by introducing probabilistic inference to optimize patch perception problem among various layers with considerable efficiency.
5. Acknowledgements
This work was supported by National Natural Science Foundation of China (No. 60875012): Research on parallelity, hierarchy and feedback in image understanding based on Synergetic and (No. 60905005): Research on natural image based on solid image model. It was also supported by Specialized Research Fund for the Doctoral Program of Higher Education of China (No. 2009111110015): Research on Image Understanding methods based on rapid Visual Perception.
REFERENCES
- Y. Wang and S.-C. Zhu, “Perceptual Scale-Space and Its Applications,” International Journal of Computer Vision, Vol. 80, No. 1, 2008, pp. 143-165. doi:10.1007/s11263-008-0138-4
- Y. S. Kang and H. Nagarashi, “Depth perception from a 2D Natural Scene Using Scale Variation of Texture Patterns,” Ieice Transactions on Information and Systems, Vol. 3, 2006, pp. 1294-1298. doi:10.1093/ietisy/e89-d.3.1294
- J. M. Henderson, “Human Gaze Control during RealWorld Scene Perception,” Trends in Cognitive Sciences, Vol. 7, No. 11, 2003, pp. 498-504. doi:10.1016/j.tics.2003.09.006
- J. Vogel and B. Schiele, “Semantic Modeling of Natural Scenes for Content-Based Image Retrieval,” International Journal of Computer Vision, Vol. 72, No. 2, 2007, pp. 133-157. doi:10.1007/s11263-006-8614-1
- M. M. Silva, J. A. Groeger, et al., “Attention-Memory Interactions in Scene Perception,” Spatial Vision, Vol. 19, No. 1, 2006, pp. 9-19. doi:10.1163/156856806775009223
- B. Reimer, L. A. D’Ambrosio, et al., “Behavior Differences in Drivers with Attention Deficit Hyperactivity Disorder: The Driving Behavior Questionnaire,” Accident, Analysis and Prevention, Vol. 37, No. 6, 2005, pp. 996- 1004. doi:10.1016/j.aap.2005.05.002
- D. Le and E. Izquierdo, “Global-to-local Oriented Rapid Scene Perception,” 9th International Workshop on Image Analysis for Multimedia Interactive Services, Klagenfurt, 7-9 May 2008, pp. 155-158.
- S. Lazebnik, C. Schmid, et al., “Beyond Bags of Features: Spatial Pyramid Matching for Recognizing Natural Scene Categories,” Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, 9 October 2006, pp. 2169-2178.
- M. Gheiratmand, H. Soltanian-Zadeh, et al., “Towards an Inclusive Computational Model of Visual Cortex,” 8th IEEE International Conference on Bioinformatics and BioEngineering, Athens, 8-10 October 2008, pp. 1-5.
- S. Grossberg, “Towards a Unified Theory of Neocortex: Laminar Cortical Circuits for Vision and Cognition,” Computational Neuroscience: Theoretical Insights into Brain Function, Vol. 165, 2007, pp. 79-104. doi:10.1016/S0079-6123(06)65006-1
- A. Oliva and A. Torralba, “Modeling the shape of the scene: A Holistic Representation of the Spatial Envelope,” International Journal of Computer Vision, Vol. 42, No. 3, 2001, pp. 145-175. doi:10.1023/A:1011139631724
- T. Yuehua, M. Skubic, et al., “Performance Evaluation of SIFT-Based Descriptors for Object Recognition,” Proceedings International Multi Conference of Engineering and Computer Scientists, Hong Kong, 17-19 March 2010, pp. 978-988.
- B. Johnson and Z. Xie, “Unsupervised Image Segmentation Evaluation and Refinement Using a Multi-Scale Approach,” Isprs Journal of Photogrammetry and Remote Sensing, Vol. 66, No. 4, 2011, pp. 473-483. doi:10.1016/j.isprsjprs.2011.02.006
- N. Bianchi-Berthouze, “Subjective Perception of Natural Scenes: The Role of Color,” Proceedings of SPIE—The International Society for Optical Engineering, Santa Clara, 21 January 2003, pp. 1-13.
- A. H. Assadi, “Perceptual Geometry of Space and Form: Visual Perception of Natural Scenes and Their Virtual Representation,” Proceedings of SPIE—the International Society for Optical Engineering, Shanghai, 29 July 2001, pp. 59-72.
- I. Gurevich, “The Descriptive Techniques for Image Analysis and Recognition,” Proceedings of the Second International Conference on Computer Vision Theory and Applications, Barcelona, 8-11 March 2007, pp. 223-229.
- P. Adibi and R. Safabakhsh, “Joint Entropy Maximization in the Kernel-Based Linear Manifold Topographic Map,” Proceedings of International Joint Conference on Neural Networks, Orlando, 12-17 August 2007, pp. 1133- 1138. doi:10.1109/IJCNN.2007.4371117
- K. Shi and Z. Song-Chun, “Mapping Natural Image Patches by Explicit and Implicit Manifolds,” IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, 17-22 June 2007, pp. 1-7.
- C. Pavlopoulou and S. X. Yu, “Indoor-outdoor Classification with Human Accuracies: Image or Edge Gist?” IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, San Francisco, 13- 18 June 2010, pp. 41-47. doi:10.1109/CVPRW.2010.5543428
- C. Guo and L. Zhang, “A Novel Multiresolution Spatiotemporal Saliency Detection Model and Its Applications in Image and Video Compression,” Ieee Transactions on Image Processing, Vol. 9, No. 1, 2010, pp. 185-198.
- M. L. Gong and Y. H. Yang, “Quadtree-based Genetic Algorithm and Its Applications to Computer Vision,” Pattern Recognition, Vol. 37, No. 8, 2004, pp. 1723-1733. doi:10.1016/j.patcog.2004.02.004
- F. Porikli, L. Davis, et al., “A Comprehensive Evaluation Framework and a Comparative Study for Human Detectors,” IEEE Transactions on Intelligent Transportation Systems, Vol. 10, No. 3, 2009, pp. 417-427. doi:10.1109/TITS.2009.2026670
- A. Holub and P. Perona, “A Discriminative Framework for Modelling Object Classes,” IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, 20-26 June 2005, pp. 664-671.
- M. Everingham, L. Van Gool, et al., “The Pascal Visual Object Classes (VOC) Challenge,” International Journal of Computer Vision, Vol. 88, No. 2, 2010, pp. 303-338. doi:10.1007/s11263-009-0275-4

