Open Journal of Soil Science
Vol.4 No.5(2014), Article ID:45919,6 pages DOI:10.4236/ojss.2014.45020
Determining and Mapping Soil Erodibility Factor (Case Study: Yamchi Watershed in Northwest of Iran)
Rasool Imani, Hoda Ghasemieh, Mohammad Mirzavand
Faculty of Natural Resources and Geoscience, University of Kashan, Kashan, Isfahan, Iran
Email: rasool.imani@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 12 March 2104; revised 12 April 2014; accepted 19 April 2014
ABSTRACT
Among Universal Soil Erosion Equation (USLE) factors (R, K, L, S and P), Soil Erodibility Factor (K) is one of the most important and key factors which determines soil particles resistance to be detachment by water erosion (rainfall and/or runoff) forces. In fact, K factor is the rate of soil loss per rainfall erosion index unit and affected by 6 parameters including soil primary particles (silt, sand and clay), organic matter content and also permeability and structure of soil. The USLE nomograph is one of the most rapid and common methods for calculating K factor based on mentioned parameters. In this study, 38 samples of surface soil (0 - 15 cm) were collected from Yamchi watershed and the percentage of silt, sand, clay and organic matter content were determined in soil laboratory. Also textures of soil samples were determined to choice soil permeability and structure class codes based on United States Department of Agriculture (USDA) published information. Using USLE nomograph equation, K factor was calculated for each soil sample and based on kriging interpolation method, soil erodibility factor (K) map was constructed for entire study area which average soil erodibility factor and average standard error of interpolated map were 0.442 and 0.0076 t∙ha∙h∙ha−1∙Mj−1∙mm−1, respectively.
Keywords:K Factor, Kriging, USLE, Yamchi

1. Introduction
Detachment of soil particles by wind and/or water forces which is named soil erosion [1] becomes a global problem especially in vulnerable and fragile environments [2] [3] . Soil erosion has widespread and serious negative effects on agricultural production, water quality, biodiversity, useful life of reservoir dams and many other environmental risks [4] [5] . A worldwide estimation showed that arable land is lost at a rate of more than 10 million hectare per year [2] and this is serious threat especially in agriculture based countries like Iran. Therefore determination of soil loss sensitivity is one of the key prerequisites for soil erosion prediction and also choosing a suitable management practices which is toward sustainable progress.
The Universal Soil Loss Equation (USLE) developed by Wischmeier and Smith in 1978 [6] is an empirical soil erosion model that is used most frequently by professionals and technicians to predict soil loss in water erosion [2] [7] . USLE and its successor the Revised Universal Soil Loss Equation (RUSLE) are base technology in a number of other erosion models like SWAT, ACNPS, Watem/Sedem and EPIC [8] and both are related to the rain erosivity factor (R), soil erodibility factor (K), slope length factor (L), slope steepness factor (S), cover management factor (C) and support practice factor (P) [9] . Among these factors, soil erodibility factor (K) is one of the key factors that required for soil erosion determination and/or prediction across the world [10] and was found strongly correlated with soil loss [11] .
Soil erodibility is related to the integrated effects of rainfall, runoff and infiltration on soil loss and is commonly called the soil erodibility factor (K) which represents the effect of soil properties and soil profile characteristics on soil loss [12] . The K factor has been recently used as an indicator of erosion because of its susceptibility to particulate detachment and transport by erosion agents [3] . Up to now, two basic methods have been introduced for K factor determination. First method is direct measurement of K factor from standard plots whichis cumbersome and expensive but more accurate. Second method is USLE nomograph which was derived by Wischmeier et al. in 1971 [13] that although have law accuracy rather than direct method, due to its low cost and time needs, have a wide usage [14] . In this method based on soil properties include primary particles (silt, sand and clay), organic matter content, permeability and structure of soil, K factor is calculated.
In contrast to importance of K factor in soil loss prediction, numerous studies have been done in this field.
Wang et al. (2001) assessed the uncertainty of soil erodibility values published from the soil survey of Coryell county of Texas in USA in spatial prediction of soil loss by comparing them with the soil erodibility values driven from a set of soil samples and they resulted that the K value from soil samples produce reliable prediction map of soil erodibility [9] . Bahrami et al. (2005) published a fuzzy system to obtain k factor as output using its dependent parameters (parameters need for USLE nomograph) as inputs and by comparing k values attained with USLE model with fuzzy system driven K values, they found the applicability of that system [15] . Vaezi et al. (2010) determined the soil erodibility factor (K) in the northwest of Iran using both direct field measured soil loss rate of runoff plots and indirect USLE nomograph. Their results showed that the nomograph would considerably lead to over-estimation of soil erodibility in entire the study area [7] . Auerswald et al. (2014) developed a set of equations that fully emulates the USLE nomograph which facilitates the K factor calculation and supersedes the cumbersome reading of the nomograph [8] .
According to the absence of K factor information in Iran and its major importance especially in small-scale regions like watershed level, the objective of this study was to determination of soil erodibility factor (K) in Yamchi watershed using USLE nomograph. Results of this study can aid in USLE model and its successor (RUSLE) running to determine or predict soil loss that extremely affect the agricultural production and also the reservoir of Yamchi dam that is constructed in downstream of this watershed.
2. Methods and Materials
2.1. Study Area
The study area which has been named Yamchi watershed is located in west of Ardabil province in the northwest of Iran and geographically extend from 37˚51'53'' to 38˚14'33''N and 47˚46'26'' to 48˚05'34''E (Figure 1). This watershed is located between Sabalan in the north and Bozghoosh Mountains in the south of study area. Total area of watershed is 562.7 Km2 that 71.5% (approximately 402.38 Km2) of area is located in Ardabil province and 28.5% (appr. 160.32 Km2) is located in the East Azarbayjan province. Rangelands and agriculture with 51% and 46% of total area respectively, are the most common land use type in the entire study area. The climate is semi-arid and average rainfall is 303 mm that mostly occur in winter and spring and due to the high elevation which differ from 4380 m in the north (Sabalan mount) to 1560 m from sea level in the outlet, snow is the most common form of rainfall. Average annual temperature is 13˚C. Yamchi reservoir dam is constructed on downstream of this watershed and can be influenced by management practices in watershed.

Figure 1. Location of the study area and soil samples location.
2.2. Soil Erodibility Factor (K)
To estimate soil erodibility factor, the USLE nomograph published by Wischmeier et al. (1971) was used which is accordance Equation (1).
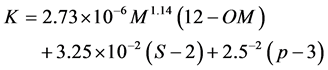 (1)
(1)
where K is soil erodibility factor (t∙ha∙h∙ha−1∙Mj−1∙mm−1) and M is texture from the first 15 cm of soil surface and is calculated using Equation (2), based on soil primary particles percentage. OM is % of organic matter content that could be determined in laboratory, S is soil structure code and P is soil permeability class and both can be obtained from USDA published documents based on soil texture [13] .
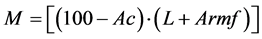 (2)
(2)
where Ac is % of clay (<0.002 mm), L is % of silt (0.002 - 0.05 mm) and Armf is % of very fine sand (0.05 - 0.1 mm) [16] .
In this study, 38 samples of surface soil (0 - 15 cm) were collected from Yamchi watershed (Figure 1) and the percentage of silt, sand, clay and organic matter content were determined in soil laboratory to investigate the soil erodibility factor (K) in Yamchi watershed using USLE nomograph. Also soil samples texture were determined using percentage of primary particle based on USDA soil texture triangle in TAL software. Then according to each soil sample texture, S and P values were obtained from the National Soils Handbook No 430 (USDA 1983) [17] in which each soil texture is assigned a Structure code and permeability class.
Using Equations (1) and (2), soil erodibility factor (K) was calculated for each soil samples. Finally using kiriging interpolation method which is widely used in several researches [7] [9] [16] [18] [19] in this field, soil erodibility factor map was constructed for inter study area.
3. Results
3.1. Soil Properties
Soil primary particles (silt, sand and clay) and organic matter content distribution maps constructed using kriging interpolation method in Arc Map®10.1 are shown in Figure 2.
This maps show that the northern and southern parts of study area have less silt content than eastern and western parts. Most of the area has sand content below 30% and clay content in north and south of study area is more than central parts. Also western parts have high organic matter content in comparison to the west. The average standard errors of the kriging interpolation maps were 0.94 %, 1.53%, 1.36% and 0.18% for the silt, sand, clay and organic matter content percentage respectively.
Also silt, sand and clay content percentage distribution for each soil sample on USDA soil texture triangle is shown in Figure 3. The analysis showed that most samples contain 20% to 55% silt, 10% to 50% sand and 15% to 44% clay and clay-loam texture which observed in 13 samples, is the most common soil texture class.
3.2. Soil Erodibility Factor (K)
Kriging method was used to interpolate and estimate the K factor value in unknown points based on K value of known points (38 sampling points) and Soil erodibility factor spatial distribution map for entire study area was constructed in Arc Map®10.1 which is shown in Figure 4.
This map shows that western part has low erodibility factor (K) values than eastern parts. Average soil erodibility factor was estimated to be 0.442 t∙ha∙h∙ha−1∙Mj−1∙mm−1, for entire study area and about 76% of soils (29 samples) have soil erodibility factor up to 0.4 t∙ha∙h∙ha−1∙Mj−1∙mm−1. Average standard error of interpolated K factor map was 0.0076 t∙ha∙h∙ha−1∙Mj−1∙mm−1. According to importance of K factor in USLE and other related soil erosion models, this map has a significant implication in modeling and prediction of erosion and aid in determination of location and kind of soil conservation practices.
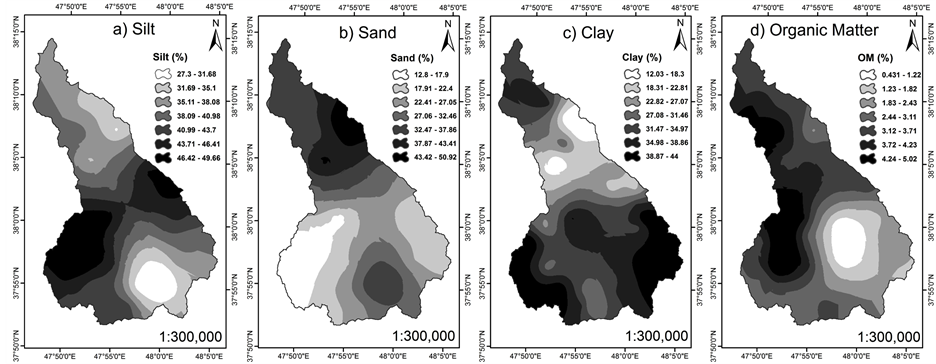
Figure 2. Silt (a); Sand (b); Clay (c) and organic matter content (d) maps for the study area.
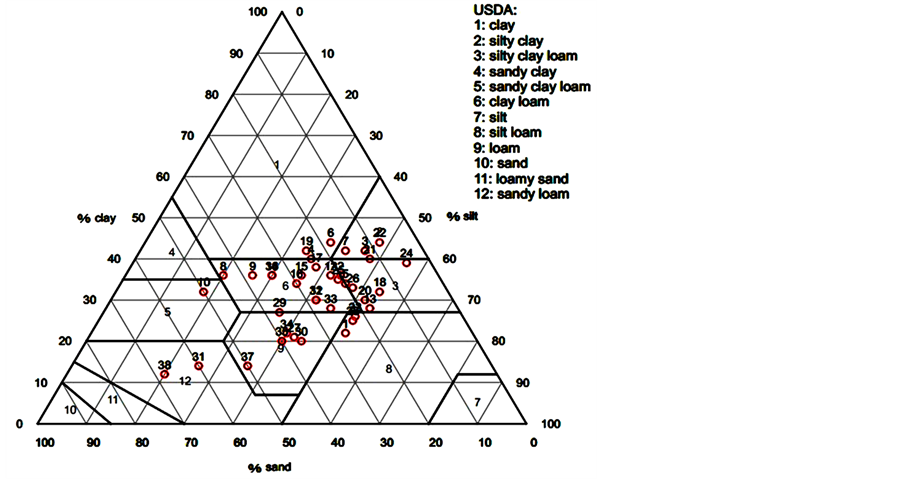
Figure 3. Distribution of sand, silt, and clay contents in the soil sampls (n = 38).

Figure 4. Soil erodibility factor map.
4. Conclusion
Soil erodibility factor (K) in Universal Soil Loss Equation (USLE) is strongly correlated with soil loss and known as a key factor in soil erosion prediction. USLE nomograph is the most common method for K factor calculation which was used in this study to determine K factor in Yamchi watershed soils. The range of K factor in study area differed from 0.3 to 0.76 t∙ha∙h∙ha−1∙Mj−1∙mm−1, and most soils had k factor more than 0.4 t ha∙h∙ha−1∙Mj−1∙mm−1. Average soil erodibility for study area was estimated to be 0.442 t∙ha∙h∙ha−1∙Mj−1∙mm−1. Eastern part has high soil erodibility and it can be due to low organic matter content, so this part is in Priority for soil conservation practices. It is suggested that the accuracy and applicability of USLE nomograph in K factor determination for this area be examined using direct measurement of K factor in standard plots.
Acknowledgements
We are grateful to University of Kashan and Mr. Mohammad Tofighi for the analysis of physical and chemical soil properties.
References
- Panagos, P., Meusburger, K., Alewell, C. and Montanarella, L. (2012) Soil Erodibility Estimation Using LUCAS Point Survey Data of Europe. Environmental Modeling & Software, 30,143-145. http://dx.doi.org/10.1016/j.envsoft.2011.11.002
- Bagarello, V., Di Stefano, C., Ferro, V., Giordano, G., Iovino, M. and Pampalone, V. (2012) Estimating the USLE the Soil Erodibility Factor in Sicily, South Italy. Applied Engineering in Agriculture, 28, 199-206. http://dx.doi.org/10.13031/2013.41347
- Manyiwa, T. and Dikinya, O. (2013) Using Universal Soil Loss Equation and Soil Erodibility Factor to Assess Soil Erosion in Tshesebe Village, Northeast Botswana. African Journal of Agricultural Research, 8, 4170-4178.
- Pimentel, D., Harvey, C., Resosudarmo, P., Sinclair, K., Kurz, D., McNair, M., Crist,S., Shpritz, L., Fitton, L., Saffouri, R. and Blair, R. (1995) Environmental and Economic Costs of Soil Erosion and Conservation Benefits. Science, 267, 1117-1123.
- Pazhouhesh, M., Gorji, M., Taheri, S.M. and Keshavarzi, A. (2011) Determination of Soil Erodibility Factor Using Fuzzy Rule Base System. International Journal of Environmental Sciences, 1, 1874-1883.
- Wischmeier, W.H. and Smith, D.D. (1978) Predicting Rainfall Erosion Losses: A Guide to Conservation Planning. USDA Agriculture Handbook No. 537, USDA, Washington DC.
- Vaezi, A.R., Bahrami, H.A., Sadeghi, S.H.R. and Mahdian, M.H. (2010) Spatial Variability of Soil Erodibility Factor (K) of the USLEin North West of Iran. Journal of Agricultural Science and Technology, 12, 241-252.
- Auerswald, K., Fiener, P., Martin, W. and Elhaus, D. (2014) Use and Misuse of the K Factor Equation in Soil Erosion Modeling: An Alternative Equation for Determining USLE Nomograph Soil Erodibility Values. Catena, 118, 220-225.
- Wang, G., Gertner, G., Liu, X. and Anderson, A. (2001) Ncertainty Assessment of Soil Erodibility Factor for Revised Nniversal Soil Loss Equation. Catena, 46, 1-14. http://dx.doi.org/10.1016/S0341-8162(01)00158-8
- Zhang, Z.G., Fan, B.E., Bai, W.J. and Jiao, J.Y. (2007) Soil Anti-Erodibility of Plant Communities on the Removal Lands in Hilly-Gully Region of the Loess Plateau. Science Soil Water Conserve, 5, 7-13.
- Tejada, M. and Gonzalez, J.L. (2006) The Relationships Between Erodibility and Erosion in a Soil Treated with Two Organic Amendments. Soil and Tillage Research, 91, 186-198. http://dx.doi.org/10.1016/j.still.2005.12.003
- Renard, K., Foster, G., Weesies, G., McCool, D. and Yoder, D. (1997) Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE). US Department of Agriculture, Agriculture Handbook No.703USDA, USDA, Washington DC.
- Wischmeier, W.H., Johnson, C.B. and Cross, B.V. (1971) A Soil ErodibilityNomograph for Farmland and Construction Sites. Journal of Soil and Water Conservation, 26, 189-193.
- Tran, L.T., Ridgley, M.A. and Duckstein, L. (2002) Application of Fuzzy Logic Based on the Revised Universal Soil Loss Equation. Catena, 47, 203-226. http://dx.doi.org/10.1016/S0341-8162(01)00183-7
- Bahrami, H.A., Vaghei, H.G., Vaghei, B.G., Tahmasbipour, N. and Taliey-Tabari, F. (2005) A New Method for Determining the Soil Erodibility FactorBased on Fuzzy Systems. Journal of Agricultural Science and Technology, 7, 115-123.
- Perez-Rodriguez, R., Marques, M.J. and Bienes, R. (2007) Spatial Variability of the Soil Erodibility Parameters and Their Relation with the Soil Map at Subgroup Level. Science of the Total Environment, 378, 166-173. http://dx.doi.org/10.1016/j.scitotenv.2007.01.044
- USDA (1983) National Soil Survey Handbook. No. 430. US Department of Agriculture, USDA, Washington DC.
- Smith, J.L., Halvorson, J.J. and Papendick, R.I. (1993) Using Multiple-Variable Indicator Kriging for Evaluating Soil Quality. Soil Science Society of America Journal, 57, 743-749. http://dx.doi.org/10.2136/sssaj1993.03615995005700030020x
- Bonilla, C.A. and Johnson, O.I. (2012) Soil Erodibility Mapping and Its Correlation with Soil Properties in Central Chile. Geoderma, 189-190, 116-123. http://dx.doi.org/10.1016/j.geoderma.2012.05.005

