Open Journal of Modern Hydrology
Vol.06 No.02(2016), Article ID:65334,15 pages
10.4236/ojmh.2016.62006
Using the Markov Chain for the Generation of Monthly Rainfall Series in a Semi-Arid Zone
Mouelhi Safouane1, Nemri Saida2, Jebari Sihem2, Slimani Mohamed3
1Laboratoire Hydrologie-CES, Ariana, Tunisie
2Institut National de Recherches en Génie Rural, Eaux et Forêt (INRGREF), Ariana, Tunisie
3Laboratoire des Sciences et Techniques de l’Eau, Institut National Agronomique de Tunisie, Tunis-Mahrajène, Tunisie

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 November 2015; accepted 3 April 2016; published 6 April 2016
ABSTRACT
Numerous methodologies have been developed in the literature for the generation of rain. However, in semi-arid areas where the irregularity of rain is contrasted, the question of the applicability of these models is still relevant. The objective of this article is to propose a development method of stochastic generator of monthly rainfall series. The present work is based on the modeling of the occurrence and the quantity of rain in a separate way. The occurrence is treated in two stages. The first step considers the Markov chain according to the occurrence of annual statements (dry, average and wet). The second step uses the monthly rankings. The amount of rain is calculated based on historical series according to the monthly rank and the annual statement noted. This method is applied to rainfall data recorded at five rainfall stations in semi-arid region of Central Tunisia. The usual and conventional statistical tests of the generated series have shown the validity of this method.
Keywords:
Stochastic Generation, Rainfall Series, Markov Chain, Semiarid, Central Tunisia

1. Introduction
The geographical location of Tunisia plays an important role in the availability of water resources. As matter of fact, 70% of its surface is exposed to arid and semi-arid climate. This country is characterized by a limited resource that is irregularly distributed in space and time. This finding represents a major challenge for managers, which explains the state’s orientation towards the mobilization of surface water and the development of management plans for the immobilization and preservation (Louati et al., 1998 [1] , Sakiss et al., 1994 [2] , Lacombe, 2007 [3] , Kingumbi et al., 2009 [4] ).
The lack of long series of rainfall observations considerably limits the estimation of water supplies. It has been shown in the literature that the generation of sets of data using short time series can lead to errors. Therefore, the most appropriate mode concerns the generation of rainfall series in conjunction with a rainfall-runoff model (Chandler, 2003 [5] , Chandler et al., 2005 [6] , Selvalingam and Miura, 1978 [7] , Rodriguez-Iturbe et al., 1987 [8] , Kim and Olivera, 2010 [9] ).
Many approaches have been developed to generate monthly rainfall series. The first approach used is the temporal disaggregation. This generation approach begins with a comprehensive series previously generated and subsequently defragmented to a time series of smaller scale. This methodology of disaggregation was originally introduced by Valencia and Schaake in 1973 [10] . It was subsequently amended by various authors (Selvalingam and Miura, 1978 [7] , Yevjevieh, 1987 [11] , Maheepala and Perera, 1995 [12] , Foufoula-Georgiou and Krajewski, 1995 [13] , Srikanthan and McMahon, 2001 [14] , Koutsoyiannis, 2003 [15] Unal et al., 2004 [16] , Miquel, 2006 [17] , Mehrotra et al., 2006 [18] , Kim and Olivera, 2010 [9] , Machiwal and Jha, 2012 [19] ).
Srikanthan and McMahon (2001) [14] as well as Koutsoyiannis (2003) [15] published a detailed literature review on generators based on monthly rainfall temporal disaggregation.
The ARIMA models have been discussed in detail by Salas et al. (1980) [20] , Fortin et al. (1994) [21] , Unal et al. (2004) [16] and Machiwal and Jha (2012) [19] . This type of model requires Gaussian series. As for global climate models, the generation of climate data is carried out on large meshes. The shift to finer mesh is through a spatial disaggregation. This method does not take into account the possible variability in the large mesh.
At the level of stochastic approach, rain is modeled by two processes, namely the occurrence and amount (Sharma and Lall, 1999 [22] ). The Markov chain has been widely used in the literature to model the occurrence of rain. Gabriel and Neumann (1962) [23] are the first to have modeled the daily rainfall using the Markov chain with two states: dry and wet. Selvalingam and Miura (1978) [7] compared the different methods based on Markov chain developed by several authors.
The monthly rainfall in semi-arid areas, particularly in Tunisia, is essentially characterized by the presence of zero values. In a study of regionalization of monthly rainfall distribution laws in Tunisia, Merzougui and Slimani (2012) [24] showed that no statistical law was adjustable for the months of June, July and August. The annual rainfall is unevenly and very randomly split between the months.
The present article proposes to adopt a response to the difficulty of adjusting a statistical law to the monthly rainfall series in the semi-arid region in Tunisia. This work is based on a new method of application of the Markov algorithm for the generation of ranks between 1 and 12 for each month, and then the generation of the states for years (dry, wet or average) and finally, to assign monthly rain values to these ranks according to the year based on the observations of history.
The first part of this article is devoted to describing the study area as well as the characteristics of rain through five stations of the Tunisian semi-arid. The second part is devoted to the mode of application of the Markov algorithm. The last part presents the results and discussions.
2. Study Site and Data
Characteristics of rain in the area of central Tunisia
The proposed methodology for the generation of the rain has first required the study of the time series of rainfall. This last step is essential for the determination of variables characterizing the choice of the approach of this generation. Indeed, the study of the historical behavior of the data series allows achieving an adequate adaptation of the generation method. In Tunisia, several studies have been interested in assessing the variable “rain” by considering varying time steps (Bargaoui, 1983 [25] , Camus, 1985 [26] , Sakiss et al., 1994 [2] , Thabet and Thabet, 1995 [27] , Zahar and Laborde et al., 1998 [28] , Kingumbi, 2009 [4] , Merzougui and Slimani, 2012 [24] ).
A study of the succession of dry, humid and average scenarios was conducted on annual rainfall series to provide a clear cyclical. According to Sakiss et al. (1994) [2] , one year is considered dry if the annual total is 40% below the annual average, very dry if the annual total was 60% below the average, a humid year if the annual total is 40% more than average rain. Finally, one year is very humid if the annual total is 60% more than average rain.
In this article, only three scenarios were adopted. They are presented as follows:
(1) The year is considered average if the annual rainfall varies between −40% and + 40% of the inter-annual average;
(2) The year is considered humid when the total of the registered year exceeds 40% of the inter-annual average;
(3) The year is considered dry if the total is less than 40% of the inter-annual average.
The annual rainfall series recorded in the five stations, subject of the present work are illustrated in Figure 1. These series show a very irregular and random succession of dry, humid and average scenarios. No clear cyclicity has emerged.



Figure 1. The annual rainfall recorded at stations: Haffouz (a); Kairouan (b); Sidi Saad (c) Sbiba (d); Kasserine (e).
3. Data Used
The rain generator developed in this article has been applied in five rainfall stations in central Tunisia (Figure 2). The characteristics of the monthly rainfall data recorded at these stations are summarized in Table 1. The months of October and September show the highest average. The months of June, July and August have the lowest averages for all stations. The coefficients of variation are high for the months that are the most and least rainy, thereby illustrating the strong irregular rainfall in the study area.
To characterize the distribution of annual rainfall depending on the month, we have undertaken a ranking of months of each year through the amount of monthly rainfall recorded. The ranks of each month take values from 1 to 12. Table 2 shows the frequencies of appearance of these ranks for each month and thereafter the contribution
Figure 2. Rainfall stations.
Table 1. Statistics characteristics of rain recorded in the five studied rainfall stations.
Table 2. Frequency of occurrence (%) of ranks from 1 to 12 for each month for the stations: (a) Sidi Saad; (b) Sbiba; (c) Haffouz; (d) Kairouan; (e) Kasserine.
of monthly rainfall to the annual precipitation. The examination of tables allows seeing that the monthly rainfall distribution is quite irregular. The month of October although on average the rainiest was found in 13% of cases during the period 1956-2010, first rank, 22% in third, 11% and the ninth and the last 2% for the Sidi Saad station. Monthly values reach their maximum everywhere during the months from September to May. The least rainy months might be September as it might be another month. However, the month of July has the highest frequency for the least rainy months. The month of October, which has the highest average monthly inter-annual is 7% of the time in rank 12 and only 17% of the time in the front row. This finding illustrates the irregularity of rain and corroborates with the results of the work already mentioned.
4. Development of a Rain Generator
The available approaches in the literature for the generation of monthly rain present constraints and assumptions that limit its use. These models are developed in wetlands with different characteristics from those of arid and semi-arid. Given the characteristic of the contrasted irregularity of the average rainfall, the Markov model seems to be the most appropriate in this study area to generate monthly rainfall data based on the ranks.
A Markov model is a stochastic pattern in which the evolution of future states depends only on the present state and not the past states. The Markov chain designates the process of Markov in a discrete time that models the evolution of discrete amounts X over time that can take a finite number of states X = X1, X2 = X, X = Xn and passes from the state Xi to the instant t to the Xj state to the next instant t + 1 with a conditional probability Pij (Bargaoui, 1983 [2] ).
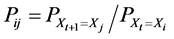 . (1)
. (1)
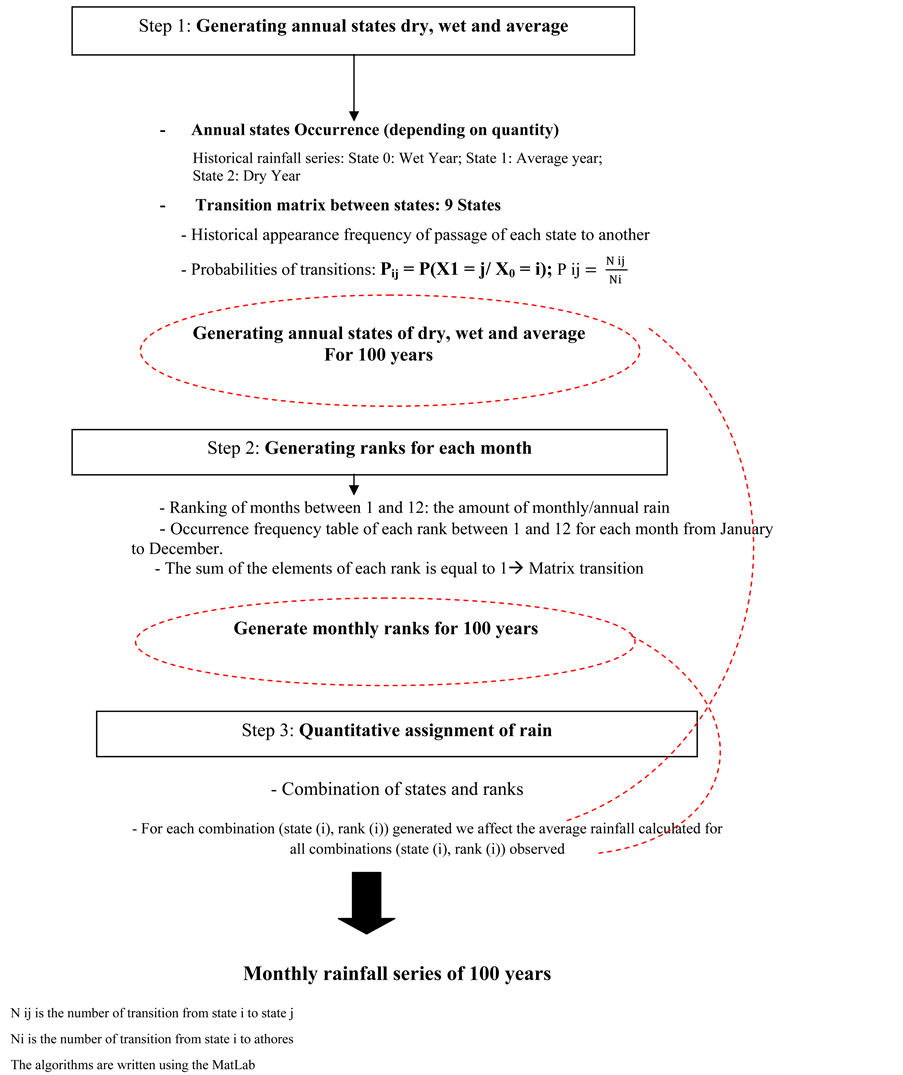
The method proposed in this article is based on three steps:
1) The first step is to generate annual returns of dry, wet and average by using the Markov chain. The corresponding matrix transition is determined by the frequency of historical occurrence of passage of each state to another.
2) The second is to generate monthly ranks ranging from 1 to 12 for each month. The matrix transition is developed by the historical frequency of appearance of each rank and for each month.
3) Depending on the month, the generated ranking and the corresponding state of the year generated, the amount of rain is affected depending on the average of the history regarding each rank for each month and each corresponding status.
Generating annual states:
In the Markov chain, rain occurrence is modeled by states that can be dry and wet or more states depending on the amount of rain. Selvalingam and Miura (1978) [7] and Allen and Haan (1975) [29] are the first to consider several states of occurrence depending on the amount of rain and not just two dry and wet conditions.
This present work has considered three annual reports: State 0 (wet year), State 1 (average year) and State 2 (dry year). The study of the historical series allows describing the appearance of these dry, wet and average scenarios.
The transition from one state to another has developed the matrix transition. This latter is formed by the probabilities of transitions Pij, which is the probability of going to state j knowing that we are at the state i which is calculated by the following equation:
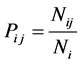 (2)
(2)
where Nij is the number of transition from state i to state j and Ni is the number of transitions from state i to any other state. Thus, we have 9 situations described in Table 3.
The station “Haffouz” was chosen here as an example to illustrate the process of generation of states. Table 4 describes the number of occurrence of each state during the historical period from 1968 to 2011. The matrix transition is shown in Table 5. A 100-year generation of annual statements (dry, wet and average) was carried out subsequently, based on the matrix transition and the Markov model. Table 6 shows only 15 years of generation as an example.
Generation of ranks for each month:
After the ranking of months between 1 and 12 depending on the amount of rainfall recorded in that month by contributing to the annual quantity, the appearance frequency table of every rank between 1 and 12 for each month from January to December is an array of size 12 * 12. Within this array, the element of each rank is equal to 1. Therefore, we assumed that this table is the matrix transition to generate monthly ranks of 100 years. For the “Haffouz” station, Table 7 shows the matrix transition monthly ranks. The ranks of months of the year 2011 are considered as the initial condition for the generation of ranks of 100 years. As an example, Table 8 only shows the ranks generated for 15 years.
Table 3. Transition matrix of the states.
Table 4. Number of occurrence of states.
Table 5. Transition matrix of states for the Haffouz station. Humid state (0), medium state (1), dry state (2).
Table 6. Generated annual states for the period of 15 years. Humid state (0), average state (1), dry state (2).
Table 7. Transition matrix for the ranks of the Haffouz station.
Table 8. Monthly rankings generated for a period of 15 years for Haffouz station.
Quantitative assignment of rain:
After generating the ranks for each month and the annual statement (dry, humid, medium) for future 100-year series, we sought a method to estimate the corresponding quantities of rain. The methods are based on generating rainfall following static laws cannot be applied herein since no law is adjustable for the months of June July and August (Merzougui and Slimani, 2012) [24] . The method used herein is to calculate based on the observed series, the average monthly rainfall according to the rank and status of the corresponding year as shown in Table 9, which summarizes this methodology. The allocation of the amount of the average rainfall is calculated thereafter for each month depending on the generated rank as well as the corresponding generated annual state.
5. Results and Discussion
The series generated by the methodology outlined in the preceding paragraph are shown in Figure 3 for five stations.
The principle of stochastic simulation models is to generate random variables that must meet the statistical structure of the process to be reproduced (Miquel, 2006 [17] ). A monthly rainfall generator aims to preserve the monthly statistical characteristics. In fact, in case of aggregation of these data the annual series of characteristics observed are not obviously preserved. The reliability model is judged by its ability to reproduce the statistical characteristics comparable to those of historical series (Selvalingam and Miura, 1978 [7] , Salas et al., 1980 [20] , Unal et al., 2004 [16] , Kim and Olivera, 2010 [9] , Kim and Olivera, 2012 [30] ). These features are essentially the means and coefficients of variation.
The characteristics of generated and observed rainfall are comparable for all months except for the month of September (Figure 4). This can be explained by the high variability of rainfall recorded in that month. This month brought together the entire strong flood that occurred. The control of chronic homogeneity is considered another test to ensure the reliability of the model and representativeness of the generated series, the method used herein is a graphic test of simple accumulated monthly rainfall totals.
Figure 5 shows that no breakage or a change in slope appears on the right of monthly totals for all stations from where the homogeneity of the observed series is generated. Figure 6 shows the autocorrelation coefficients between the staggered series and series of 1 to 7 for the generated and observed range of the five stations. It is clear that the coefficients of the two series are still between 1 and −1.



Figure 3. Series of monthly rain generated and observed in the resorts: Sbiba (a); Kasserine (b); Sidi Saad (c); Kairouan (d); Haffouz (e).





Figure 4. Comparison between the statistical characteristics of the observed and generated series: Haffouz (a); Kasserine (b); Sbiba (c); Sidi Saad (d); Kairouan (e).



Figure 5. Simple cumulative curve of monthly totals of stations: Haffouz (a); Kairouan (b); Kasserine (c); Sbiba (d); Sidi Saad (e).





Figure 6. Comparison of autocorrelation coefficients (offset of 1 to 7) for the generated and observed series of the following stations: Haffouz (a); Kairouan (b); Kasserine (c); Sbiba (d); Sidi Saad (e).
Table 9. Calculation of the observed monthly rainfall.
6. Conclusion
This study has shown the constraints that limit the application of conventional methods of generating rain in a semi-arid environment such as Tunisia. The model developed on Tunisian rainfall stations generates the occurrence and amount separately. The occurrence was generated by annual statements and monthly ranks by using the Markov chain. The amount of rain has been calculated by the observed series for each month depending on the status and rank. The results show that the model has preserved the statistical characteristics of every month except for the month of September which shows high variability due to heavy floods that usually occur in this month. The study of this month (September) in a separate way constitutes the perspective of the present work.
Cite this paper
Mouelhi Safouane,Nemri Saida,Jebari Sihem,Slimani Mohamed, (2016) Using the Markov Chain for the Generation of Monthly Rainfall Series in a Semi-Arid Zone. Open Journal of Modern Hydrology,06,51-65. doi: 10.4236/ojmh.2016.62006
References
- 1. Louati, M.H., Khanfir, R., Alouini, A., El Euch, M.L., Marzouk, A. and Frigui, L. (1998) Stratégie de secteur de l’eau en Tunisie à long terme 2030. Ministère de l’agriculture, Tunisie.
- 2. Sakiss, N., et al. (1994) La pluviométrie en Tunisie a-t-elle changé depuis 2000 ans ? Tunis Institut National de la Météorologie & Institut National Agronomique de Tunisie.
- 3. Lacombe, G. (2007) Evolution et usage de la ressource en eau dans un bassin versant aménagé semi-aride: Le cas de Merguellil en Tunisie centrale. Thèse de doctorat, Université Montpellier II.
- 4. Kingumbi, A., Bargaoui, Z. and Hubert, P. (2009) Investigations sur la variabilité pluviométrique en Tunisie centrale. Journal des Sciences Hydrologiques, 50, 493-508.
- 5. Chandler, R.E. (2003) Moment-Based Inference for Stochastic-Mechanistic Models. Internal Report No. 7, DEFRA Project Improved Methods for National Spatial-Temporal Rainfall and Evaporation Modeling for BSM.
- 6. Chandler, R.E. and Onof, C. (2005) Single-Site Model Section and Testing. Internal Report No. 11, DEFRA Project Improved Methods for National Spatial-Temporal Rainfall and Evaporation Modelling for BSM.
- 7. Selvalingam, S. and Miura, M. (1978) Stochastic Modeling of Monthly and Daily Rainfall Sequences. American Water Resources Association, 14, No. 5.
- 8. Rodriguez-iturbe, I., Cox, D.R. and Isham, V. (1987) Some Models for Rainfall Based on Stochastic Point Processes. Proceedings of Royal Society of London Series A—Mathematical Physical and Engineering Sciences, 410, 269-288.
- 9. Kim, D. and Olivera, F. (2010) Improving Stochastic Rainfall Generators. Improving Stochastic Rainfall Generators World Environmental and Water Resources Congress, Providence, 16-20 May 2010, 4.
- 10. Valencia, D. and Schaake, J. (1973) Disaggregation Process in Stochastic Hydrology. Water Resources Research, 9, No. 3.
- 11. Yevjevieh, Y. (1987) Stochastic Models in Hydrology. Stochastic Hydrology and Hydraulics, 1, 17-36.
http://dx.doi.org/10.1007/BF01543907 - 12. Maheepala, S. and Perera, B. (1995) Monthly Hydrologic Data Generation by Disaggregation. Journal of Hydrology, 178, 277-291.
http://dx.doi.org/10.1016/0022-1694(95)02834-X - 13. Foufoula-georgiou, E. and Krajewski, W. (1995) Recent Advances in Rainfall Modeling, Estimation and Forecasting. Reviews of Geophysics, Supplement, US National Report to International Union of Geodesy and Geophysics, 1125-1137.
- 14. Srikanthan, R. and Mcmahon, T. (2001) Stochastic Generation of Annual, Monthly and Daily Climate Data: A Review. Hydrology and Earth System Sciences, 5, 653-670.
- 15. Koutsoyiannis, D. (2003) Rainfall Disaggregation Methods: Theory and Applications. Workshop on Statistical and Mathematical Methods for Hydrological Analysis, Roma.
- 16. Unal, N., Aksoy, H. and Akar, T. (2004) Annual and Monthly Rainfall Data Generation Schemes. Stochastic Environmental Research and Risk Assessment Journal, 18, 245-257.
- 17. Miquel, J. (2006) Chapitre 5: Hydrologie statistique Introduction à l’Etude des Processus Hydrométéorologiques Application à la Prédétermination des Débits de Crues. Ecole Nationale des Ponts et Chaussées.
- 18. Mehrotra, R., Srikanthan, R. and Sharma, A. (2006) A Comparison of Three Stochastic Multi-Site Precipitation Occurrence Generators. Journal of Hydrology, 331, 280-292.
http://dx.doi.org/10.1016/j.jhydrol.2006.05.016 - 19. Machiwal, D. and Jha, M.K. (2012) Stochastic Modelling of Time Series. In: Machiwal, D. and Jha, M.K., Eds., Hydrologic Time Series Analysis: Theory and Practice, Springer Netherlands, Dordrecht, 85-95.
http://dx.doi.org/10.1007/978-94-007-1861-6_5 - 20. Salas, J.D., Delleur, J.W., Yevjevich, V. and Lane, W.L. (1980) Applied Modeling of Hydrologic Time Series. Water Resources Publications, Littleton.
- 21. Fortin, V., Ouarda, T. B.M.J., Rasmussen, P.F. and Bobée, B. (1994) Revue bibliographique des méthodes de prévision des débits. Revue des Sciences de l’Eau, 10, 461-487.
http://dx.doi.org/10.7202/705289ar - 22. Sharma, A. and Lall, U. (1999) A Nonparametric Approach for Daily Rainfall Simulation. Mathematics and Computers in Simulation, 48, 361-371.
http://dx.doi.org/10.1016/S0378-4754(99)00016-6 - 23. Gabriel, K.R. and Neumann, J. (1962) A Markov Chain Model for Daily Rainfall Occurrence at Tel Aviv. Quarterly Journal of the Royal Meteorological Society, 88, 90-95.
http://dx.doi.org/10.1002/qj.49708837511 - 24. Merzougui, A. and Slimani, M. (2012) Régionalisation des lois de distribution des pluies mensuelles en Tunisie. Hydrological Sciences Journal, 57, 668-685.
http://dx.doi.org/10.1080/02626667.2012.670702 - 25. Bargaoui, Z. (1983) Contribution de l’étude de la pluie dans la région de Tunis. Thèse de doctorat, Institut National Polytechnique de Toulouse, Toulouse.
- 26. Camus, H. (1985) Etude pluviométriques bassins versants des oueds Zeroud et merguellil Tunis: DGRE/OROSTOM.
- 27. Thabet, B. and Thabet, C. (1995) Modélisation de variables aléatoires: Cas de la pluviométrie. Cahiers Options Méditerranéennes, 9, 135-150.
- 28. Zahar, Y. and Laborde, J.P. (1998) Génération stochastique d’averses et de leurs indices d’érosivité pour la simulation de la dynamique érosive en Tunisie centrale. Journal des Sciences Hydrologiques, 46, 243-253.
http://dx.doi.org/10.1080/02626660109492819 - 29. Allen, D.M. and Haan, C.T. (1975) Stochastic Simulation of Daily Rainfall. Research Report No. 82, Water Resources Institute, University of Kentucky, Lexington.
- 30. Kim, D. and Olivera, F. (2012) Relative Importance of the Different Rainfall Statistics in the Calibration of Stochastic Rainfall Generation Models. Journal of Hydrologic Engineering, 17, 368-376.
http://dx.doi.org/10.1061/(ASCE)HE.1943-5584.0000453









