Received 23 July 2015; accepted 6 October 2015; published 9 October 2015

ABSTRACT

The hydrodynamics in Lake Naivasha, a shallow endorheic lake, are simulated using the Delft3D Flow Module to investigate the major driving forces of hydrodynamics in the lake. The results showed wind as the major forcing. The shallow zones of the lake showed currents movement in the same direction as the wind while the deep zones showed currents movements against the wind direction. These findings were confirmed and further explained using an idealized model. Limited exchange between the Crescent Lake (crater lake which is temporally separated from the lake during low water levels) and the main lake was observed. These findings can explain the spatial variability of the water quality in the lake. Similar studies could be used in exploratory studies of the spatial-temporal variability in water quality in other shallow water systems.

Keywords:

Hydrodynamics, Water Quality, Shallow Lakes, Wind-Driven Currents, Lake Naivasha

1. Introduction

The hydrodynamics play an important role in sediment redistribution and transport of the associated contaminants in shallow lakes through upwelling and vertical mixing in lakes. The upwelling and vertical mixing processes could lead to nutrient release from the sediment layer and therefore accelerating eutrophication, which results to high turbidity. This information can help in implementation of eutrophication mitigation measures such as dredging, nutrient reduction, or biological control management options.

Research has portrayed numerical models as powerful tools for simulation of hydrodynamics and water quality in shallow lakes. Zhu et al. [1] not only simulated currents from three dimensional hydrodynamic characteristics but also employed a two-dimensional water quality numerical model to simulate diffusion and transport of pollutants in Lake Yangchenghu. You et al. [2] investigated eutrophication in Lake Taihu by simulating the effects of hydrodynamics on phosphorus fluxes. Other researchers have modelled sediment resuspension and transport [3] -[6] . Although hydrodynamics have been modelled for other lakes in the world, there has not been any other similar study in Lake Naivasha.

Lake Naivasha is one of the lakes that have transformed from a clear lake to a turbid lake in the recent decades [7] . The understanding of hydrodynamics and other processes governing the water quality in Lake Naivasha would provide information on the driving forces of the turbidity dynamics. The main aim of this study is to assess the major driving forces in hydrodynamics. This study provides information on the major forcings of the currents in Lake Naivasha.

The paper is organised as follows. Section 2 introduces the study site. In Section 3, the Delft3D Flow Module is described as applied to Lake Naivasha. The scenarios of typical wind and river outflow are also shown in Section 3. The results are presented in Section 4 while a verification done with an idealised model is shown in Section 5. The findings are discussed in Section 6 and conclusions are presented in Section 7.

2. Study Area: Lake Naivasha

This study was conducted in Lake Naivasha, a shallow endorheic lake situated on the floor of the Eastern Rift Valley in Kenya at 1885 m above sea level. It lies at latitude 0˚46'S and longitude 36˚22' (Figure 1) within a

complex geological arrangement of volcanic rocks and sedimentary deposits. The mean temperature around Lake Naivasha is approximately 25˚C. December-March is the hottest period (30˚C) while July is the coldest month (23˚C). Precipitation is bi-modal in March/April/May and in October/November at an average of 650 mm year⁻¹. During the rainy season, the main lake occupies about 150 km² but shrinks to about 100 km² during the dry season [8] . The main inputs into the lake are mainly from the River Malewa and the River Gilgil that account for 80% and 10% of the lakes discharge, respectively (Table 1). The remaining inflow comes from other less significant rivers around the lake such as the River Karati and other small ephemeral streams along the southern shore of the lake that carry surface runoff to the lake during heavy rainfall. On the eastern side lies the Crescent Crater Lake which is much deeper (approximate maximum depth of 17 m in October 2011) than the main lake which is somewhat separated from the main lake especially at low water levels. The west and the southern lakeshores are surrounded by high hills while the North East is relatively flat. More details on the study area are discussed in Ndungu et al. [7] [9] [10] ).

3. Lake Naivasha Hydrodynamic Model

A horizontal grid of 40 m by 40 m was developed inside the lake boundary. Depth measurements collected in October 2011 were interpolated using QUICKIN Module of Delft3D and used to generate the depth file (bathymetry). Water inflow from rivers, air temperatures, and wind play a role in water movements and were therefore taken into account in this study. A constant value of 23˚C was adopted based on the October 2011 water temperature field data [9] . We choose to adopt the Manning roughness option with a fixed value of 0.02 m^1/2∙s⁻¹ [11] . Viscosity and diffusivity values were 1 m²∙s⁻¹, and 10 m²∙s⁻¹, respectively. Absolute flux, total solar radiation option was used because it takes into account the relative humidity, air temperature and heat losses due to evaporation and convection. Air temperature, relative humidity, total radiation, wind speed and direction data were acquired from weather analytics station^TM sensor number 427,286 close to Moi South Lake Road (southern edge of the lake) in Naivasha. Weather analytics stations are composed of 35 × 35 km grid squares and therefore are area based weather stations. More information on the dataset can be obtained from: http://www.weatheranalytics.com/weather-products/.

The main discharge into the lake is from the River Malewa which accounts for 80% of the discharge. Discharge data from Water Resource Management Authority (WRMA) gauging station 2GB1 was used as input. Although the Gilgil and Karati rivers’ discharges are less significant, the values were estimated from field data [12] .

To assess the main driving forces of water movement in Lake Naivasha, various scenarios were simulated (Table 1). Wind direction varies over the year as illustrated by the wind rose diagram (Figure 2). The plot was generated from daily average wind speed and direction data in 2011. The major wind directions were found to be around 45˚, 90˚ and 135˚. Therefore, the simulations were performed on these three wind directions. There were no winds from the west and southwest because the area consists of hills, which block the wind.

The highest wind speed for this study was determined by selecting the speed that exceeded about 90% of the year 2011 to avoid working with extreme outliers. The value was found to be 3.6 ms⁻¹ (Figure 3 (d)). The highest discharge was determined in a similar way by plotting the cumulative frequency distribution of Gilgil, Malewa and Karati rivers discharge, respectively (Figures 3(a)-(c)). The selected discharge values were 1.6, 19.7 and 0.4 m³/s in Gilgil, Malewa and Karati rivers, respectively.

4. Hydrodynamic Modeling Results

The results of the hydrodynamic model for each scenario are shown in maps. The simulation at zero wind speed

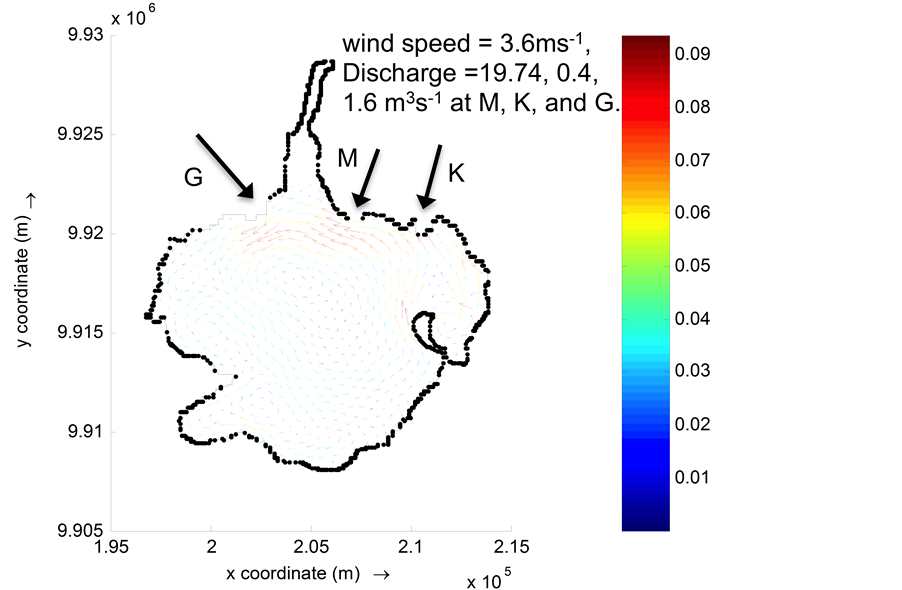
and high discharge showed northwest water circulation concentrated only around the discharge locations (Figure 4(a)). The rest of the lake was virtually calm. However, the simulation with the zero discharge and high (3.6 m・s⁻¹) wind speed from north east and eastern direction (45˚ and 90˚) showed two circular motions at the north and southern regions of the lake (Figure 4(b), Figure 4(c) and Figure 5). The velocities were relatively higher in the shallow areas as compared to the deep zones. In the northern part, the currents curve and move against the wind direction around the deep zone (middle of the lake) in an anticlockwise direction. The southern part also curves towards the middle of the lake but in a clockwise direction. High wind speed and high discharge showed a similar pattern as that of zero discharge and high wind speed scenario indicating that wind is the dominant driving force for the currents in the lake. The wind from the southeast (135˚) also showed currents motion against the wind direction in the deep zones (Figure 6).

5. Idealized Hydrodynamics Model

In order to make a further verification for Lake Naivasha hydrodynamics, which enabled physical interpretation, we developed an idealized model as described in Mathieu et al. [13] .

A closed rectangular basin of length 2L and width 2B was considered (Figure 7). The coordinates x and y

were taken to be the along-basin and cross-basin direction, such that the basin boundaries were at x = −L, L and y = −B, B. The vertical coordinate z points upward, and z = η denotes the free surface elevation with respect to the undisturbed water level z = 0 and the bed level at z = −h. In this simple model h varies only in y direction h(y). The wind stress is indicated by tw.

A constant wind forcing was imposed and the linearized mass and momentum equations were solved assuming the pressure to be hydrostatic. The non-dimensional terms were introduced to account for the boundary condition. The horizontal velocity and transport were then modelled together with the stream function.

We choose the following typical values: B = 10 km, L = 12 km, h = 10 m and a constant vertical eddy viscosity of 0.012 m²∙s⁻¹.

For scenario 4, the shallow parts of the lake show currents moving in the direction where the wind is blowing, while the deeper regions show the currents moving against the wind direction (Figure 8). The longer the arrow, the stronger the currents. So, the results are similar to those of the Delft3D model.

In both the idealised model and the Delft3D model, the currents move against the wind direction in the deep area. The results are likely because with the assumption of a steady state the depth averaged momentum equation would be expressed as:

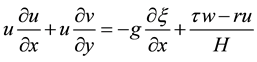(1)

where 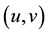represents flow velocity vector, x and y are coordinates that align with along- and cross-basin di-

rections, 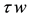is the wind shear stress, H is the depth while r is the bottom frictional coefficient and 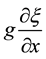is the surface gradient. In a steady situation 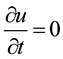thus 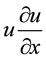and 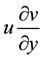are negligible, when the pressure is assumed to be hydrostatic. Therefore, Equation (1) can be rewritten as:

(2)

Hence,

(3)

In Lake Naivasha we have a deep area around the middle and shallow areas at the edges of the lake. In the shal-

low parts, H is small and therefore the term dominates making the velocity positive (u) which means that the current is in the direction of the wind. In deep water, H is larger, and therefore the term dominates

making the velocity u negative, which means that the currents move against the wind direction.

6. Discussion

Several computational hydrodynamic models have been developed [14] -[17] . Reviews of the existing hydrodynamic models can be found in [18] -[23] . The choice of the model to use depends on the nature of the associated problem, data availability, the available time to solve the problem and the ability of the model to simulate the ecosystem adequately. Delft3D has been used in this study because of its robust modelling capabilities, which enabled us to model the lake in respect to the bathymetry rather than having a uniform depth. The Delft3D model results portrayed circular motions in the main lake, which suggests some mixing around the middle. These currents could contribute to vertical transport/upwelling of sediments, which results in release of adsorbed nutrients into the water column. The availability of the nutrients in the water column could enhance proliferation of algal biomass leading to high turbidity levels. However, more exploration on the sedimentation processes which include transport and dissipation of particles, as well as internal wave motion and the subsequent re-suspension of sediments to the water column could provide immense information especially if dredging is considered as a management option.

The mid-lake and the southern region of the lake are similar in terms of water quality parameters [7] [24] which could be explained by the circular motion in the main lake. The northern region showed high current velocities, which could be attributed to the shallow depth. Ndungu et al. [7] showed dominance of coloured dissolved particles in the northern region which could be as a result of the high current velocities which keep small particles in suspension [7] . Crescent Lake showed limited exchange with the main lake especially at 45˚ wind direction. Previous studies have shown that the Crescent Lake is distinct from the main lake [24] .

Zero and maximum discharge in combination with highest wind speed simulation outcomes were similar indicating the influence of the rivers’ discharge on currents was limited. Therefore, wind is the major forcing factor in current direction and magnitude rather than the discharge in Lake Naivasha. Kranenburg [25] has shown the effect of wind driven chaotic advection on transport of a passive tracer in shallow lakes with a conclusion that time dependent velocity fields can produce complex advection patterns. The circulation of other Rift Valley lakes such as Lake Victoria in Kenya are known to be wind driven [26] [27] . Ssebuggwawo et al. [28] simulated the hydrodynamics of Lake Victoria using Delft3D and found the simulations to be in agreement with currents measured in the field. Although other researchers have mentioned wind-driven turbulence in Sonachi Crater Lake, which is part of the Lake Naivasha system, no other study has been undertaken in hydrodynamic simulation for Lake Naivasha main lake.

7. Conclusion

From the hydrodynamic model, we conclude that currents are mainly wind-driven in Lake Naivasha. The currents could be responsible for the mass transport from the input rivers which impacts on the spatial-temporal variability in water quality in Lake Naivasha. This is because the current seems to propel fast in the shallow northern region and assumes circular motions in the deeper central part of the lake. There exists mixing (denoted by circular motions) in the main lake, which can enhance nutrient redistribution and eventually impact on the algal biomass growth and hence the turbidity levels. The mixing indicates that the main lake could be well mixed. The study also shows limited exchange between the Crescent Lake and the main lake. This explains the reason behind the spatial variability described in Ndungu et al. [7] [10] .

Acknowledgements

The authors of this paper gratefully acknowledge the WOTRO Science for Global Development for funding this research work. We also appreciate the administrative assistance provided by International Institute for Geo- information and Earth Observation (ITC) particularly through Prof. Anne van der Veen, and Drs. Robert Becht. We acknowledge the NOAA/NCEP (National Center for Environmental Prediction) for the provision of the high resolution Climate Forecast System Reanalysis (CFSR) data set. We are also grateful for the financial support from China Scholarship Council (CSC), which covered the expenses for Wenlong Chen PhD study.

Cite this paper

Jane N.Ndungu,WenlongChen,Denie C. M.Augustijn,Suzanne J. M. H.Hulscher, (2015) Analysis of the Driving Force of Hydrodynamics in Lake Naivasha, Kenya. Open Journal of Modern Hydrology,05,95-104. doi: 10.4236/ojmh.2015.54009

References