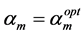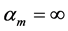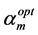Open Journal of Modern Hydrology
Vol.04 No.03(2014), Article ID:47580,10 pages
10.4236/ojmh.2014.43007
Spatio-temporal Prediction of Root Zone Soil Moisture Using Multivariate Relevance Vector Machines
Bushra Zaman, Mac McKee
Utah Water Research Laboratory, Utah State University, Logan, USA
Email: b.zaman@aggiemail.usu.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 April 2014; revised 30 May 2014; accepted 30 June 2014
ABSTRACT
Root zone soil moisture at one and two meter depths are forecasted four days into the future. In this article, we propose a new multivariate output prediction approach to root zone soil moisture assessment using learning machine models. These models are known for their robustness, efficiency, and sparseness; they provide a statistically sound approach to solving the inverse problem and thus to building statistical models. The multivariate relevance vector machine (MVRVM) is used to build a model that forecasts soil moisture states based upon current soil moisture and soil temperature conditions. The methodology combines the data at different depths from 5 cm to 50 cm, the largest of which corresponds to the depth at which the soil moisture sensors are generally operational, to produce soil moisture predictions at larger depths. The MVRVM test results for soil moisture predictions at 1 m and 2 m depth on the 4th day are excellent with RMSE = 0.0131 m3/m3 for 1 m; and RMSE = 0.0015 m3/m3 for 2 m forecasted values. The statistics of predictions for 4th day (CoE = 0.87 for 1 m and CoE = 0.96 for 2 m) indicate good model generalization capability and computations show good agreement with actual measurements with R2 = 0.88 and R2 = 0.97 for 1 m and 2 m depths, respectively. The MVRVM produces good results for all four days. Bootstrapping is used to check over/under-fitting and uncertainty in model estimates.
Keywords:
relevance vector machines, statistics, predictions, soils, soil moisture, data management

1. Introduction
Root zone soil moisture is regarded as key factor governing surface water and energy balances and plays a vital role in hydroclimatic and environmental predictions. Soil moisture content (SMC) measurements are important for irrigation scheduling and crop yield forecast modeling, understanding rainfall/runoff generation processes. Information on soil moisture helps in explaining processes related to crop growth, forest dynamics and other vadose zone processes which play a vital role in water resources planning and management.
Soil moisture varies both in space and time because of spatial and temporal variations in precipitation, soil, topographic features, and vegetation characteristics [1] . The spatio-temporal prediction of SMC is difficult though capturing these variations and having an accurate estimation of soil moisture is necessary for soil and land survey [2] [3] , soil and land evaluation [4] , hydrologic modeling and watershed management [5] [6] . Also, there is a need to develop methods for estimating SMC which make the best possible use of ancillary information, particularly that which is relatively cheap to obtain [7] - [9] . Much work has been done in the past where soil moisture at larger depths was retrieved using surface soil moisture estimates [10] - [14] . The surface soil moisture content is physically related to root-zone soil moisture through diffusion processes, and both surface and root-zone soil layers are commonly simulated by land surface models (LSMs) [15] [16] demonstrated the relationship between the soil moisture profile and surface soil moisture and fluxes. It was found that soil moisture can be predicted using low-level atmospheric and meteorological inputs [17] [18] .
SMC retrieval using different techniques has been the subject of research for almost four decades. In general, soil moisture measurements are made as point measurements, mainly using gravimetric, nuclear, electromagnetic, tensiometric, or hygrometric techniques [19] , or by measuring SMC with imbedded sensors, such as time- and frequency-domain reflectometers (TDRs and FDRs). Physically based models for soil moisture estimation include the Soil-Plant-Atmosphere-Water (SPAW) model of [20] [21] - [23] , the US Department of Agriculture Hydrograph Laboratory (USDAHL) model [24] [25] , and the Sacramento Soil Moisture Accounting (SAC-SMA) Model [26] [27] used by the National Weather Service River Forecast System (NWSRFS) [28] , soil vegetation atmosphere transfer (SVAT) models, among others. However, the difficulty associated with measurement of the physical parameters required by these models serves as an impediment.
This has furthered the interest of researchers to look for data-driven modeling tools such as artificial neural networks (ANNs) [29] - [31] , higher order neural networks [32] , support vector machines (SVMs) [33] [34] . [18] used soil moisture and meteorological data to generate SVM predictions for four and seven days ahead. The RVM and SVM models were used for forecasting soil moisture five days in the future by [35] . In the present study, we are applying a relatively new data-driven tool, the multivariate relevance vector machine (MVRVM) for soil moisture estimation. The purpose of this research was to develop a new model which forecasts soil moisture at different root zone depths, so both spatial and temporal predictions are done simultaneously. With this goal in mind, past measurements of soil moisture at shallower depths, soil temperature and precipitation were used as inputs to a MVRVM model that forecasts soil moisture at large depths and for several days in the future. This model used available data acquired by the data collection station for previous days. The procedure employs point analyses, and no horizontal spatial patterns are taken into consideration. This learning machine tool automatically learns to recognize complex patterns that reside in data and that can be exploited to model input-output relationships. This technique, which has generated promising results, has never been tried before.
2. Multi-Variate Relevance Vector Machine (MVRVM)
“Sparse Bayesian Learning” is used to describe the application of Bayesian automatic relevance determination (ARD) concepts to models that are linear in their parameters. The motivation behind the approach is that one can infer a regression model that is both accurate and sparse in that it makes its predictions using only a small number of relevant basis functions that are optimally selected from a potentially large initial set. A special case of this concept is the RVM which is applied to linear kernel models. The RVM was originally introduced by [36] [37] proposed an extension of the sparse Bayesian regression model developed by [38] and this extension enables a single relevance vector machine (RVM) to handle multiple output dimensions. The multivariate regression code developed by [37] is an open source code. This code was used as a base to build the MVRVM model which was particular to this application.
The data set is in the form of input-output pairs, 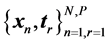 , where x is the input matrix, t is the target
, where x is the input matrix, t is the target
vector, P is the number of output dimensions and N is the number of observations. The major goal is to learn a model of dependency of the outputs on the inputs with the objective of making accurate predictions for previously unseen values of x [39] . Each output vector (tr) is written as 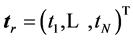 and is expressed as the sum of an approximation vector
and is expressed as the sum of an approximation vector  and an “error” vector, the elements of which are considered as independent samples from some noise process
and an “error” vector, the elements of which are considered as independent samples from some noise process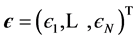 :
:
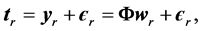 (1)
(1)
where, wr = weight vector for the rth component of the output vector tr and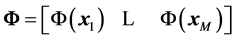 , the N ´ M “design” matrix whose columns comprise the complete set of M “basis vectors”. According to the sparse Bayesian approach [39] , “the errors are conventionally assumed to be zero-mean Gaussian, with variance
, the N ´ M “design” matrix whose columns comprise the complete set of M “basis vectors”. According to the sparse Bayesian approach [39] , “the errors are conventionally assumed to be zero-mean Gaussian, with variance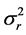 . The parameter σ2 is estimated from the data and the error model implies a multivariate Gaussian likelihood for the target vector tr:
. The parameter σ2 is estimated from the data and the error model implies a multivariate Gaussian likelihood for the target vector tr:
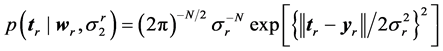 (2)
(2)
“There are as many parameters in the model as training examples, therefore we would expect maximum likelihood estimation of wr and σ2 from (2) to lead to severe over-fitting” [39] . A prior constraint over wr is imposed by adding a complexity penalty to the likelihood to avoid overfitting. The “hyperparameters” are used to constrain an explicit zero-mean Gaussian prior probability distribution over the weights, wr:
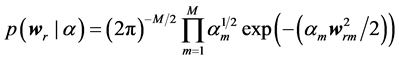 (3)
(3)
[38] introduced “M” independent hyperparameters, 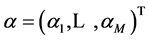 , where each element α is called a hyperparameter that determines the relevance of the associated basis function φj, which is one component of the basis vector Φ. Each hyperparameter individually controls the strength of the prior over its associated weight. It is this form of prior that ultimately makes the model sparse. Given α, the posterior parameter distribution conditioned on the data is given by combining the likelihood and prior within Bayes’ rule:
, where each element α is called a hyperparameter that determines the relevance of the associated basis function φj, which is one component of the basis vector Φ. Each hyperparameter individually controls the strength of the prior over its associated weight. It is this form of prior that ultimately makes the model sparse. Given α, the posterior parameter distribution conditioned on the data is given by combining the likelihood and prior within Bayes’ rule:
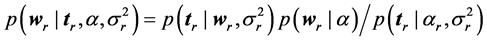 (4)
(4)
and is Gaussian N(μr,Σr) with, 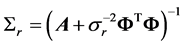 and
and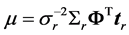 , where A is defined as
, where A is defined as 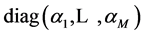 .
.
The algorithm proposed by [37] for training an RVM with multivariate outputs by finding the optimal hyper- parameters is as follows:
(1) Initialization of the noise variance σr and the hyperparameter α: σr = variance of tr ´ 0.1, r Î 1, ×××, P; α = infinity (∞); P = number of output dimensions
(2) Iterate: (a) Compute 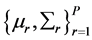 using
using
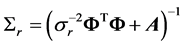 ; (5)
; (5)
(b) Compute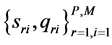
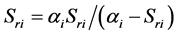

(c) Find the basis function, Φm, and the corresponding optimal hyperparameter 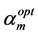
L(α) using the following Equations:

If 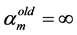
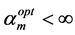
If 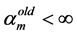
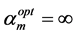
If 
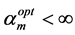
(d) Re-estimate the noise parameters using,
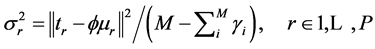
The optimal hyperparameters and the noise parameters are then used to obtain the optimal weight matrix:
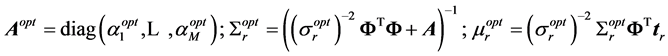
Readers interested in detailed descriptions of the model are referred to [37] .
3. Data Description
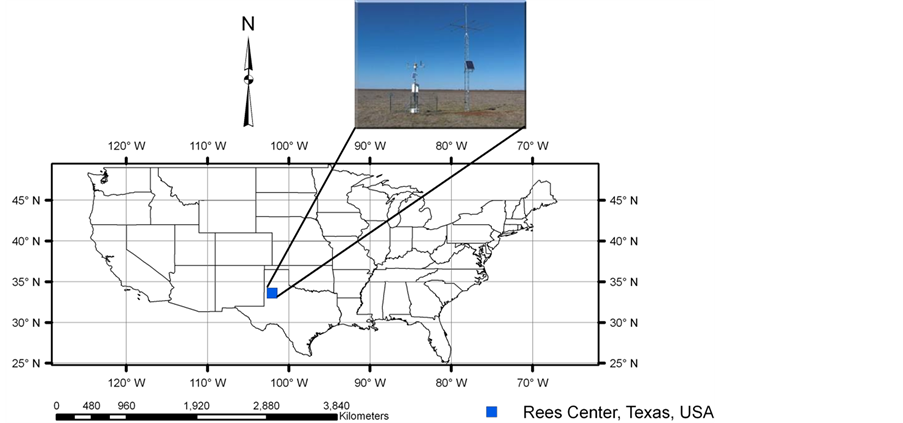
The data used for this study were taken from the Soil Climate Analysis Network (SCAN) site at Rees Center, Texas, USA. There are about 86 SCAN stations across the United States where daily and hourly measurements for meteorological and soil moisture data are made using various sensors and instruments. Of these 86 stations, most collect soil moisture data up to a depth of 40 inch (around 100 cm), and there a few which collect soil moisture data up to a depth of 80 inch (around 200 cm). Rees Center, Texas is one such SCAN station which collects soil moisture data up to a depth of 200 cm. In this particular application, meteorological inputs (precipitation and soil temperature) and soil moisture data were used. The location of the data collection station at SCAN Site, Rees Center, Texas is 33˚37'N and 102˚02'W, at an elevation of 3333 feet (1015.9 meter (m)) (Figure 1). This Sensor is reporting since March 10, 2005 and it collects hourly and daily time series data. The sensor recordings are instantaneous and it reports a single observation, taken at the beginning of an interval, which is midnight for a daily time series data. The instrument used for measuring soil moisture and soil temperature is a Hydra Probe Soil Sensor (2.5 volt) with an accuracy of +/− 0.03 wfv (m3∙m−3) and +/− 0.6 Degrees Celsius (From −10˚C to 36˚C) respectively. Detailed information about the data is available on the website http://www.wcc.nrcs.usda.gov/scan.
4. Methodology
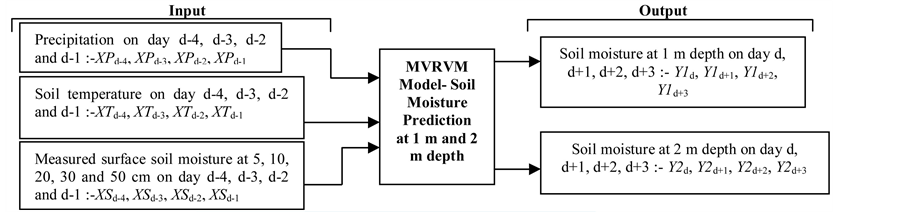
Our goal was to forecast root zone soil moisture at 1 and 2 m depths. This was done by assimilating soil moisture (m3/m3) at shallower depths (5, 10, 20, 30 and 50 cm), soil temperature (Celsius) and precipitation (mm), and predicting soil moisture at depths of 1 and 2 m. The time series soil moisture data for 12 months were downloaded from the Natural Resource Conservation service (NRCS) website. A stratified sampling of the 12 months of data was carried out and the training and testing data were extracted from this stratified sample. The test data were kept aside for validating the performance of the machine. The stratified sampling was done to train the MVRVM model for different values of soil moisture in different seasons. It was observed that normalization of the data between −1 and 1 produced better results as compared to the case where raw data were used. Hence the data were normalized. The MVRVM model was trained with 227 days of soil moisture data spread over a year and corresponding soil temperature and meteorological data. The inputs to the model were precipitation, soil temperature, and soil moisture data on days “d−4”, “d−3”, “d−2”, “d−1”. The output of the model was forecasted soil moisture values at “d”, “d+1”, “d+2” and “d+3”. Time steps were in days. The performance of the model was tested with 100 days of input data spread over a year. Figure 2 shows the flow diagram of the model approach in the training phase. Three analyses were done with different inputs. For the first analysis, the MVRVM model was trained using soil moisture at depths of 5, 10, 20, 30 and 50 cm below ground surface, soil temperature (Celsius), and precipitation (mm) as inputs. The second analysis was similar to the first one but it only used soil moisture at 5 and 10 cm, soil temperature (Celsius), and precipitation (mm) as inputs to train the MVRVM model. The third analysis used soil moisture at 30 and 50 cm, soil temperature (Celsius), and precipitation (mm) as inputs to train the MVRVM model. The output in all three cases was soil moisture at 1 and 2 m depths on d, d+1, d+2 and d+3, i.e. four days into the future. The latter two analyses were carried out to observe the variation in the model output when moisture in the topsoil (5, 10 cm) and then at larger depths (30, 50 cm) were used to train the learning machine. Figure 2 shows the MVRVM model approach. The model inputs were: x = [XPd−4, XSd−4, XTd−4, XPd−3, XSd−3, XTd−3, XPd−2, XSd−2, XTd−2, XPd−1, XTd−1, XSd−1], where, d = time (day) and the model outputs were: y = [Y1d, Y2d, Y1d+1, Y2d+1, Y1d+2, Y2d+2, Y1d+3 Y2d+3].
To test the degree of association between the observed and estimated data, goodness-of-fit evaluation measures were used. The mean absolute error (MAE), a linear measure and root mean square error (RMSE), a quadratic scoring rule, were used to measure average magnitude of error. The index of agreement (IoA) and coefficient of efficiency (CoE) were also used to check model performance. These statistics are calculated as:
Figure 1. Location of data collection station.
Figure 2. Flow diagram for MVRVM model approach.
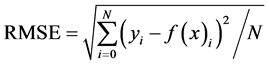
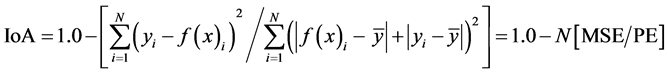
where N is the number of testing samples. In this formulation, y and f(x) are the measured and modeled values, respectively. The RMSE and MAE measure the error between the actual data and modeled values. Large values of RMSE or MAE mean that the difference between the actual measurements and the modeled values is large; hence the model is not performing well enough. Both the MAE and RMSE can range from zero to infinity. Lower values are better. The RMSE has the same dimensionality as the data and therefore it is easy to interpret. The IoA is calculated by comparing an observed group variance with an expected random variance. It varies from zero (inferior model) to one (excellent model). Potential Error (PE) is defined as the sum of the squared absolute values of the distances from f(x)i to ӯ and from yi to ӯ and represents the largest value that it can attain for each actual observation/simulated value pair [40] . CoE ranges from −∞ (inferior model) to 1 (excellent model) [41] . Thus, a value of zero for the CoE indicates that the observed mean, ӯ, is as good an estimator as the model, while negative values indicate that the observed mean is a better estimator than the model [42] .
5. Results and Discussion
The goal of this research was to forecast spatio-temporal estimates of root zone soil moisture at depths of 1 and 2 m below ground surface. A MVRVM model was used to build the model. This section discusses the selection of model parameters, MVRVM model performance, and the bootstrap analyses. Evaluation of RVM performance was based on selection of optimal kernel width and optimized iterations. Several trials were performed for obtaining the optimal values of these parameters. For the MVRVM, the parameters α and σ2 were automatically estimated by the learning procedure. The optimal kernel width for the MVRVM model was obtained through a trial and error procedure, and the optimal number of iterations was obtained by plotting parameter beta against the number of iterations. The number at which the value of the parameter beta became almost constant was considered to be optimal. Figure 3 shows the plot of the parameter beta with respect to the number of iterations.
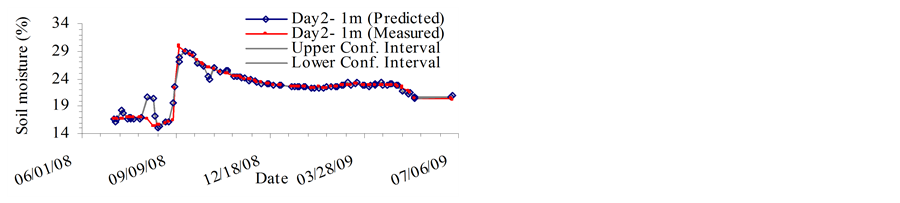
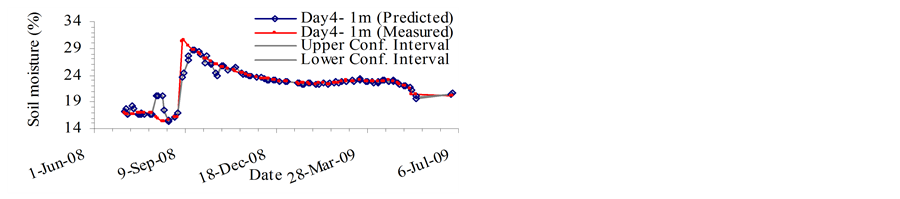
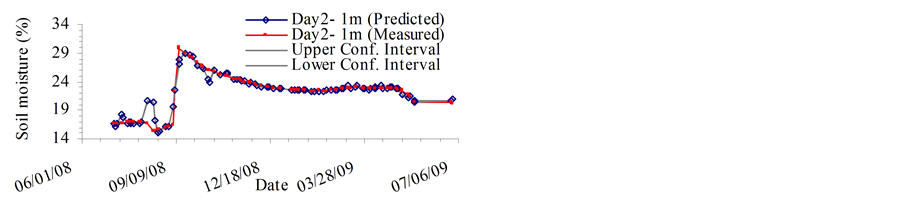
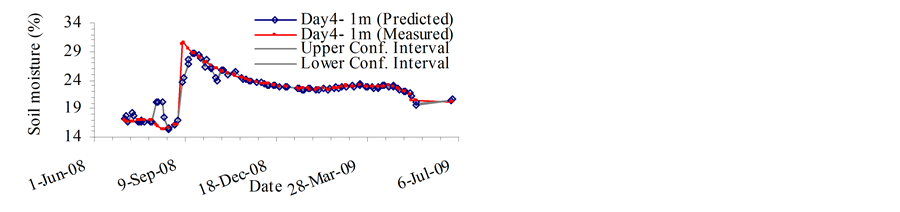
The MVRVM model exhibits good performance. Figure 4 and Figure 5 show predicted outputs versus original data and the confidence bounds for the test phase. The results produced by the MVRVM model in the test phase for SMC estimate at 1 m depth for four consecutive days are shown in Figures 4(a)-(d). The MVRVM model showed good results with the forecasted values of soil moisture closely following the pattern of the time series. Table 1 shows the goodness-of-fit test results for the test data. The average maximum value of soil moisture at 1 m depth is about 30%, and the minimum is about 15%. The correlation result for the MVRVM model on the fourth day at 1 m depth (see Table 1) demonstrated good performance (R2 = 0.877 and RMSE = 1.31%), with an IoA of 0.96 and the CoE of 0.87. This indicated that the observed data and modeled values were close. The bias is very small indicating that the estimator is robust. The average MAE for 1 m depth was 0.5 which suggested that model estimates differed from the data on an average of 0.50%. The results produced by the MVRVM model in the test phase for SMC estimates at a depth of 2 m are shown in Figures 5(a)-(d). Again, the MVRVM model showed excellent results with forecasted values closely following the pattern of the time series. The average maximum value of soil moisture at 1 m depth is about 19%, and the minimum is about 15%. The correlation result for the MVRVM model on the fourth day at a depth of 2 m (see Table 1) again demonstrated good performance (R2 = 0.968 and RMSE = 0.15%), with an IoA of 0.99 and a CoE value of 0.97. This indicated that observed data and modeled values were very close. The average MAE for 1 m depth was 0.08 which suggested that model estimates differed from the data by an average of only 0.08%. The number of relevance vectors (RVs) used in the MVRVM model was 81 out of 227 training points.
Better results were obtained for soil moisture forecast at 2 m depth in comparison to those obtained at 1 m depth. The variation in moisture at larger depths is smaller than at shallower depths. Due to subdued soil moisture dynamics at 2 m depth, the machine has a simpler pattern to learn and forecasting soil moisture at 2 m depth becomes comparatively easier.
Figures 5(a)-(d) show that the soil moisture pattern is followed very accurately by the MVRVM model. The machine was able to capture the spatio-temporal variation of soil moisture at the root zone depths during peak agricultural seasons. Figure 4 and Figure 5 show that the forecast results have fairly narrow confidence bounds (at 95% confidence interval), which indicates that there is low variance in predictions. Most of the measured data points lie inside the confidence bounds, indicating that the model is robust.
The full MVRVM model used soil moisture values at four different depths as inputs: 5, 10, 30, and 50 cm for soil moisture prediction at deeper depths. Two additional analyses were done to reveal the effect of only using the surface data (5 cm and 10 cm) for prediction of soil moisture at 1 m and 2 m, and then using data at 30 cm and 50 cm for the same prediction. The SMC predictions obtained by using input data at 30 cm and 50 cm were closer to the actual soil moisture measurements (see Table 2) and this model produced better results compared to the results generated by the MVRVM model which used data at 5 cm and 10 cm (Table 3). The results for both the analyses were good but not as good as were obtained from the full MVRVM model. However, depending upon the availability of data, the MVRVM model can be applied for soil moisture prediction at larger depths. This article brings into light the capability of the MVRVM model to learn the pattern of soil moisture variation and predict acceptable estimates of soil moisture.
Bootstrapping was performed for the MVRVM model to check for over-fitting and evaluate model generalization capability. Figure 6 shows bootstrap results for RMSE, as estimated from 1000 bootstrap samples. Conforming to the nonparametric approach, no assumption was made about the form of the data, and repeated samples were drawn from the population with replacement. The basic idea is that if the sample is a good approximation of the population, the bootstrap method will provide a good approximation of the sampling distribution of the statistic, in this case, the RMSE. Although beyond the scope of this article, our goal here was to ensure good generalization of the inductive learning algorithm. A narrow confidence interval indicated that the available training dataset was adequate to determine the machine parameters. From Figure 6(a) and Figure 6(b), one could deduce rough confidence bounds that are more revealing of model performance than single values [43] . In Figure 6, we see that the RMSE values for all the three MVRVM models are centered around one maximum
Figure 3. Variation of parameter beta with number of iterations for different outputs.
Table 1. MVRVM model results (Kernel Width, r = 3, Iterations = 140).
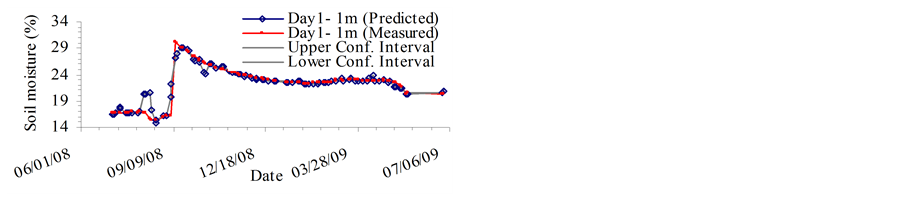
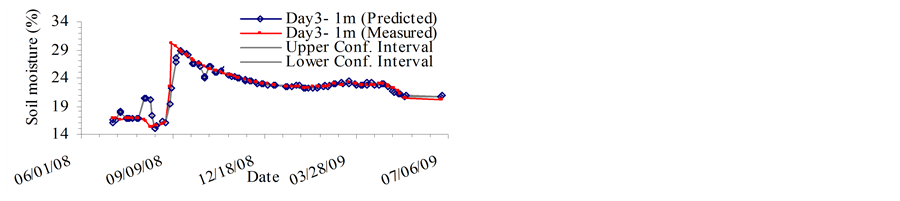
Figure 4. Root zone soil moisture prediction at 1 meter depth on Day: (a) d; (b) d+1; (c) d+2; (d) d+3. (a) Day 1: Root zone SMC at 1 m depth; (b) Day 2: Root zone SMC at 1 m depth; (c) Day 3: Root zone SMC at 1 m depth; (d) Day 4: Root zone SMC at 1 m depth.
Table 2. MVRVM model results when SMC at a depth of 30 cm and 50 cm are used as inputs.
Table 3. MVRVM model results when only surface SMC at a depth of 5 cm and 10 cm are used as inputs.
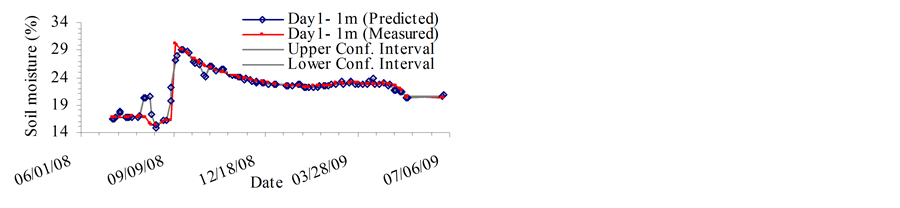
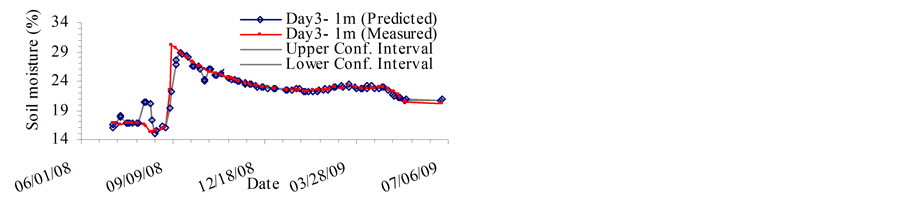
Figure 5. Root zone soil moisture prediction at 2 meter depth on Day: (a) d; (b) d+1; (c) d+2; (d) d+3. (a) Day 1: Root zone SMC at 2 m depth; (b) Day 2: Root zone SMC at 2 m depth; (c) Day 3: Root zone SMC at 2 m depth; (d) Day 4: Root zone SMC at 2 m depth.
value with highest frequency. Also the MVRVM model shows a fairly narrow confidence bound in all the cases, which implies that the model was robust and its parameter values were well determined.
6. Summary and Conclusion
This article presents a first attempt to forecast spatial and temporal variation of soil moisture simultaneously using machine learning techniques. This model is based on a sparse Bayesian learning machine approach wherein the machine learns the input output pattern with high accuracy. A MVRVM model is built for developing the prediction functions that forecast soil moisture at 1 m and 2 m depth four days into the future. Three different analyses were done using input data at different depths. The best results were obtained for the full MVRVM model where the input data at 5, 10, 30, and 50 cm depths were used. The results showed excellent performance by the machine for all four days. It was observed that the SMC predictions at 2 m depth were more accurate than those at 1 m depth. The second analysis where the SMC were predicted at 1 m and 2 m depths using data at 5 cm and 10 cm suggested that it is possible to estimate soil moisture in the root zone using surface data by applying the MVRVM model. The inputs for the third analysis were chosen keeping in mind that the soil moisture sensors are generally operational at these depths, i.e. 30 cm and 50 cm. The MVRVM model performance for this third analysis was also very good, leading to the conclusion that soil moisture conditions at larger depths can be predicted using the MVRVM model if soil moisture data from the sensors are available at 30 cm and 50 cm.
Computation of statistics of interest in conjunction with bootstrapping analyses accomplished a broad operational evaluation of the full MVRVM soil moisture model. These analyses allow us to conclude that the model


Figure 6. Bootstrap analysis results for uncertainty in the RMSE of the MVRVM model with 1000 bootstrap samples for the test phase: (a) Prediction of Soil Moisture at 1 meter depth; (b) Prediction of Soil Moisture at 2 meter depth.
can predict spatial and temporal variation of soil moisture at large depths with a high degree of accuracy. The model also had good generalization capabilities providing robustness, as demonstrated by the bootstrap analyses results. The MVRVM scheme discussed in this article can be employed to obtain soil moisture estimates from the model in real time and is a potentially useful approach for obtaining short term forecasts in situations where new data can be rapidly exploited as they become available. The results are encouraging and confirm the relevance of the proposed methodology which can benefit soil moisture monitoring and can be extended to other fields of hydrologic science.
Acknowledgements
The authors would like to thank the Utah Water Research Laboratory (UWRL) and the Utah Centre for Water Resources Research (UCWRR) for their support of this research. The authors would like to thank Garry L. Schaefer of National Water and Climate Center (NRCS) for providing help regarding data details when needed. The authors are grateful to the reviewers as their feedback helped in improving the quality of this paper.
References
- Das, N.N. and Mohanty, B.P. (2006) Root Zone Soil Moisture Assessment Using Remote Sensing and Vadose Zone Modeling. Vadose Zone Journal, 5, 296-307. http://dx.doi.org/10.2136/vzj2005.0033
- Webster, R. and Butler, B. (1976) Soil Classification and Survey Studies at Ginninderra. Soil Research, 14, 1-24. http://dx.doi.org/10.1071/SR9760001
- McKenzie, N.J. and Austin, M.P. (1993) A Quantitative Australian Approach to Medium and Small Scale Surveys Based on Soil Stratigraphy and Environmental Correlation. Geoderma, 57, 329-355. http://dx.doi.org/10.1016/0016-7061(93)90049-Q
- Fu, B. and Gulinck, H. (1994) Land Evaluation in an Area of Severe Erosion: The Loess Plateau of China. Land Degradation & Development, 5, 33-40. http://dx.doi.org/10.1002/ldr.3400050105
- Western, A.W., Grayson, R.B., Blöschl, G., Willgoose, G.R. and McMahon, T.A. (1999) Observed Spatial Organization of Soil Moisture and Its Relation to Terrain Indices. Water Resources Research, 35, 797-810. http://dx.doi.org/10.1029/1998WR900065
- Qiu, Y., Fu, B., Wang, J. and Chen, L. (2003) Spatiotemporal Prediction of Soil Moisture Content Using Multiple-Li- near Regression in a Small Catchment of the Loess Plateau, China. CATENA, 54, 173-195. http://dx.doi.org/10.1016/S0341-8162(03)00064-X
- Moore, I.D., Gessler, P.E., Nielsen, G.A. and Peterson, G.A. (1993) Soil Attribute Prediction Using Terrain Analysis. Soil Science Society of American Journal, 57, 443-452. http://dx.doi.org/10.2136/sssaj1993.03615995005700020026x
- Lark, R.M. (1999) Soil-Landform Relationships at Within-Field Scales: An Investigation Using Continuous Classification. Geoderma, 92, 141-165. http://dx.doi.org/10.1016/S0016-7061(99)00028-2
- Qiu, Y., Fu, B., Wang, J. and Chen, L. (2001) Soil Moisture Variation in Relation to Topography and Land Use in a Hillslope Catchment of the Loess Plateau, China. Journal of Hydrology, 240, 243-263. http://dx.doi.org/10.1016/S0022-1694(00)00362-0
- Camillo, P. and Schmugge, T.J. (1983) Estimating Soil Moisture Storage in the Root Zone from Surface Measurements. Soil Science, 135, 245-264. http://dx.doi.org/10.1097/00010694-198304000-00006
- Entekhabi, D., Nakamura, H. and Njoku, E.G. (1994) Solving the Inverse Problem for Soil Moisture and Temperature Profiles by Sequential Assimilation of Multifrequency Remotely Sensed Observations. IEEE Transactions on Geoscience and Remote Sensing, 32, 438-448.
- Calvet, J.C. and Noilhan, J. (2000) From Near-Surface to Root-Zone Soil Moisture Using Year-Round Data. Journal of Hydrometeorology, 1, 393-411. http://dx.doi.org/10.1175/1525-7541(2000)001<0393:FNSTRZ>2.0.CO;2
- Albergel, C., Rudiger, C., Pellarin, T., Calvet, J.C., Fritz, N., Froissard, F., et al. (2008) From Near-Surface to Root- Zone Soil Moisture Using an Exponential Filter: An Assessment of the Method Based on In-Situ Observations and Model Simulations. Hydrology and Earth System Sciences, 12, 1323-1337. http://dx.doi.org/10.5194/hess-12-1323-2008
- Calvet, J., Noilhan, J. and Bessemoulin, P. (1998) Retrieving the Root-Zone Soil Moisture from Surface Soil Moisture or Temperature Estimates: A Feasibility Study Based on Field Measurements. Journal of Applied Meteorology, 37, 371-386. http://dx.doi.org/10.1175/1520-0450(1998)037<0371:RTRZSM>2.0.CO;2
- Sabater, J., Jarlan, L., Calvet, J., Bouyssel, F. and De Rosnay, P. (2007) From Near-Surface to Root-Zone Soil Moisture Using Different Assimilation Techniques. Journal of Hydrometeorology, 8, 194-206. http://dx.doi.org/10.1175/JHM571.1
- Li, J. and Islam, S. (2002) Estimation of Root Zone Soil Moisture and Surface Fluxes Partitioning Using Near Surface Soil Moisture Measurements. Journal of Hydrology, 259, 1-14. http://dx.doi.org/10.1016/S0022-1694(01)00589-3
- Mahfouf, J.F. (1991) Analysis of Soil Moisture from Near-Surface Parameters: A Feasibility Study. Journal of Applied Meteorology, 30, 1534-1547. http://dx.doi.org/10.1175/1520-0450(1991)030<1534:AOSMFN>2.0.CO;2
- Gill, M.K., Asefa, T., Kemblowski, M.W. and McKee, M. (2006) Soil Moisture Prediction Using Support Vector Machines. JAWRA Journal of the American Water Resources Association, 42, 1033-1046. http://dx.doi.org/10.1111/j.1752-1688.2006.tb04512.x
- Song, J.L., Wang, D.H., Liu, N.J., Cheng, L., Du, L. and Zhang, K. (2008) Soil Moisture Prediction with Feature Selection Using a Neural Network. Digital Image Computing: Techniques and Applications (DICTA), Canberra, 1-3 December 2008, 130-136.
- Saxton, K.E., Johnson, H.P. and Shaw, R.H. (1974) Modeling Evapotranspiration and Soil Moisture. Transactions of the ASABE, 17, 673-677.
- Rao, A.S. and Saxton, K.E. (1995) Analysis of Soil Water and Water Stress for Pearl Millet in an Indian Arid Region Using the SPAW Model. Journal of Arid Environments, 29, 155-167. http://dx.doi.org/10.1016/S0140-1963(05)80086-2
- Arora, V.K., Singh, C. and Singh, K. (1997) Comparative Assessment of Soil Water Balance under Wheat in a Subtropical Environment with Simplified Models. The Journal of Agricultural Science, 128, 461-468. http://dx.doi.org/10.1017/S0021859697004358
- Hill, A. and Neary, V. (2009) Hydrologic Response of a Forested Sinkhole Wetland to Different Land Management Scenarios. Journal of Environmental Hydrology, 17, 1-18.
- Holtan, H., Stiltner, G., Henson, W. and Lopez, N. (1975) USDAHL-74 Revised Model of Watershed Hydrology. Technical Bulletin, No. 1518.
- Comer, G.H. and Henson, W.H. (1976) An Optimization Technique Adapted to Usdahl-74 Revised Model of Water- shed Hydrology. JAWRA Journal of the American Water Resources Association, 12, 139-146. http://dx.doi.org/10.1111/j.1752-1688.1976.tb02644.x
- Peck, E. (1976) Catchment Modeling and Initial Parameter Estimation for the National Weather Service River Forecast System. NOAA Technical Memorandum NWS Hydro-31, NWS, NOAA, DOC, Washington DC, June 1976.
- Sorooshian, S., Duan, Q.Y. and Gupta, V.K. (1993) Calibration of Rainfall-Runoff Models: Application of Global Op- timization to the Sacramento Soil Moisture Accounting Model. Water Resources Research, 29, 1185-1194. http://dx.doi.org/10.1029/92WR02617
- Burnash, R. (1995) The NWS River Forecast System-Catchment Modeling. In: Singh, V., Ed., Computer Models of Watershed Hydrology, Water Resources Publication, Colorado, 311-366.
- Atluri, V., Hung, C.C. and Coleman, T.L. (1999) An Artificial Neural Network for Classifying and Predicting Soil Moisture and Temperature Using Levenberg-Marquardt Algorithm. IEEE Proceedings Southeastcon’99, Lexington, 25-28 March 1999, 10-13.
- Chang, D. and Islam, S. (2000) Estimation of Soil Physical Properties Using Remote Sensing and Artificial Neural Network. Remote Sensing of Environment, 74, 534-544. http://dx.doi.org/10.1016/S0034-4257(00)00144-9
- Jiang, H. and Cotton, W.R. (2004) Soil Moisture Estimation Using an Artificial Neural Network: A Feasibility Study. Canadian Journal of Remote Sensing, 30, 827-839. http://dx.doi.org/10.5589/m04-041
- Elshorbagy, A. and Parasuraman, K. (2008) On the Relevance of Using Artificial Neural Networks for Estimating Soil Moisture Content. Journal of Hydrology, 362, 1-18. http://dx.doi.org/10.1016/j.jhydrol.2008.08.012
- Gill, M., Kemblowski, M. and McKee, M. (2007) Soil Moisture Data Assimilation Using Support Vector Machines and Ensemble Kalman Filter. Journal of the American Water Resources Association, 43, 1004-1015. http://dx.doi.org/10.1111/j.1752-1688.2007.00082.x
- Yang, S. and Huang, Y. (2009) Application of Support Vector Machine Based on Time Series for Soil Moisture and Nitratenitrogen Content Prediction. Computer and Computing Technologies in Agriculture II, Beijing, 18-20 October 2008, 2037-2045.
- Khalil, A., Gill, M. and McKee, M. (2005) New Applications for Information Fusion and Soil Moisture Forecasting. 8th International Conference on Information Fusion, Philadelphia, 25-28 July 2005. http://dx.doi.org/10.1109/ICIF.2005.1592050
- Tipping, M. (2000) The Relevance Vector Machine. Advances in Neural Information Processing Systems, 12, 652-658.
- Thayananthan, A., Navaratnam, R., Stenger, B., Philip, H., Torr, S. and Roberto, C. (2006) Multivariate Relevance Vector Machines for Tracking. In: Computer Vision-ECCV 2006, Graz, 7-13 May 2006, 124-128.
- Tipping, M.E. and Faul, A.C. (2003) Fast Marginal Likelihood Maximisation for Sparse Bayesian Models. Proceedings of the 9th International Workshop on Artificial Intelligence and Statistics, Florida, 3-6 January 2003, 3-6.
- Tipping, M. (2001) Sparse Bayesian Learning and the Relevance Vector Machine. Journal of Machine Learning Research, 1, 211-244.
- Legates, D.R. and McCabe, G.J. (1999) Evaluating the Use of “Goodness-of-Fit” Measures in Hydrologic and Hydroclimatic Model Validation. Water Resources Research, 35, 233-241. http://dx.doi.org/10.1029/1998WR900018
- Nash, J.E. and Sutcliffe, J.V. (1970) River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. Journal of Hydrology, 10, 282-290. http://dx.doi.org/10.1016/0022-1694(70)90255-6
- Wilcox, B.P., Rawls, W.J., Brakensiek, D.L. and Wight, J.R. (1990) Predicting Runoff from Rangeland Catchments: A Comparison of Two Models. Water Resources Research, 26, 2401-2410. http://dx.doi.org/10.1029/WR026i010p02401
- Willmott, C.J. (1984) On the Evaluation of Model Performance in Physical Geography. In: Spatial Statistics and Models, Springer, Berlin, 443-460.