Open Journal of Forestry Vol.05 No.07(2015), Article ID:59742,10
pages
10.4236/ojf.2015.57057
Estimation of Tree Crop Size across Multiple Taxa: Generalization of a Visual Survey Method
Ami Nakajima1,2*, Takashi Masaki3*, Shinsuke Koike1, Koji Yamazaki4, Koichi Kaji1
1Tokyo University of Agriculture and Technology, Tokyo, Japan
2Tama Zoological Park, Tokyo, Japan
3Forestry and Forest Products Research Institute, Tsukuba, Japan
4Tokyo University of Agriculture, Tokyo, Japan
Email: nimh42@hotmail.com, masaki@ffpri.affrc.go.jp, koikes@cc.tuat.ac.jp, yamako@j.email.ne.jp, kkaji@cc.tuat.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 July 2015; accepted 18 September 2015; published 21 September 2015
ABSTRACT
Estimating tree fruit production is important for various purposes; however, no consensus has been established on which method is appropriate over different tree species. Here the aim of this study was to assess whether the tree crop size of taxa with different fruit morphology could be accurately estimated using the visual survey method (VSM), taking into consideration errors due to the participation of different observers. Eight main tree species of temperate deciduous forests of Japan were used. Using a hierarchical Bayesian framework, the model parameters were estimated to convert the number of fruits counted by VSM to the fallen fruit density. The estimated model had a high accuracy for seven of the eight tree species. The trees of the outlier species had the smallest diameter and height, presumably resulting in false-positive errors. The model could be easily generalized for other species that were not tested in this study by adjusting the model parameters to the size of the unit used in the visual survey. The bias caused by errors depending on the observer (likely false-negatives) was not substantial. Thus, the generalized VSM proposed in this study should be useful to accurately estimate the crop size across various tree taxa with low workload.
Keywords:
Forest Regeneration, Fruit Production, Observation Error, Seed Production, Wildlife Management

1. Introduction
Estimating the trees fruit production is important for various purposes, such as understanding the reproductive strategies of trees, conserving frugivorous wildlife populations, and facilitating forest regeneration (Koenig et al., 1994; Noyce & Coy, 1990; Tsuji et al., 2006; Nakajima, 2015) . Estimation methods need to be suitable from a quantitative (cost) and qualitative (precision) perspective (Giovanni et al., 2009) . For instance, an ordered categorical index assessed visually provided a rough estimation (Perry & Thill, 1999) , but it could be conducted at low cost and could provide sufficient information in certain situations (Masaki et al., 2008; Nakajima, 2015) . However, when quantitative data on fruit production are needed, such as a measure of wildlife food availability, it is preferable to estimate absolute values, such as mass or energy per unit area, for the forest’s main species. For this purpose, the visual survey method (VSM) proposed by Koenig et al. (1994) is appropriate. It consists of scanning a portion of a tree crown using a binocular, and counting as many apparently viable acorns as possible within 15 s. Past studies demonstrated that, after the number of acorns counted by the two observers was summed, the sum had a high correlation with the density of fallen acorns of Quercuslobata, Q. douglassi and Q. agrifolia (Koenig et al., 1994) , Q. alba (Perry &Thill, 1999) , Q. ilex spp. ballota (Carevic et al., 2014) , and Fagus sylvatica (Giovanni et al., 2009) . Perry & Thill (1999) suggested that this method was preferable over other simple methods (e.g., categorical ratings) because it was probably less affected by observer bias. However, Masaki & Abe (2008) suggested that variations among observers were not negligible. Furthermore, as the studies cited above applied the method only to oaks and beeches, it was unknown whether the method was general and versatile over a wide range of tree taxa.
In this study, VSM was applied with multiple tree taxa, having various fruit and infructescence morphologies. The main tree species of temperate deciduous forests of Japan were selected, which provided fruits for the wildlife (Koike & Masaki, 2008; Masaki et al., 2012; Nakajima et al., 2012) . The total crop size can be easily obtained after assessing the crop density of a tree (fallen seeds per unit area), and multiplying it by the crown projection area, which can be estimated from the stem diameter (Gill et al., 2000; Bechtold, 2003; Condés & Sterba, 2005) . It was further aimed to develop a method to eliminate errors caused by variation among observers. Correcting observation bias is important when tree crop densities are monitored over a long period, or over a large area, because different observers are inevitably engaged in the surveys.
The aim of this study was to assess whether the fallen fruit density per unit area could be accurately estimated using VSM across multiple tree taxa by multiple observers. It was then attempted to generalize this method for application over other species untested in this study.
2. Field Methods
2.1. Study Site
Our research was conducted at two study sites. The first was the Ogawa Forest Reserve, located in the northern part of the Ibaraki Prefecture (36˚56'N, 140˚35'E, 600 - 650 m a.s.l.), hereafter denoted as Ogawa. This 100 ha reserve is an old-growth temperate deciduous forest located in the southern end of the Abukuma Mountains (Nakashizuka & Matsumoto, 2002) . This forest is dominated by Q. serrata (Masaki et al., 1992) . The second study area was the Ashio-Nikko Mountains, located across Tochigi and Gunma prefectures (36˚41'N, 139˚27'E, 700 - 2100 m a.s.l.), hereafter denoted as Ashio. The deciduous broad-leaved forests here mainly consist of Q. crispula and Castanea crenata (Nakajima et al., 2012) .
2.2. Studied Species
During 2007-2009, 45 trees of eight tree species were surveyed on the field: three Fagaceae species (Ca. crenata, Q. crispula, and Q. serrata), three Rosaceae species (Prunus verecunda, P. grayana, and Sorbus commixta), one Cornaceae species (Cornus controversa), and one Araliaceae species (Gamblea innovans). The observation units, counted using binoculars, differed between species: a fruit for Q. serrata, Q. crispula, and P. verecunda; an infructescence for P. grayana, S. commixta, Co. controversa, and G. innovans; and a cupule for Ca. crenata. Hereafter, these observation units were called as “fruits” for convenience.
To examine the difficulty in finding a unit, the width of the abovementioned units were obtained in the literature (Kitamura & Murata, 1971, 1979; Mogi et al., 2000; Satake et al., 1999a, 1999b) . Because the width of Ca. crenata cupules was not found in the literature, mature undehisced cupules were randomly sampled (n = 10), under a conspecific adult tree in Ogawa, on October 8, 2012, and their width was measured using a caliper. Table 1 summarizes the studied species, with the number and size of the sampled trees, location, year, and width of the observation units.
2.3. Visual Survey Using Binoculars
Eleven observers participated in the fruit counting using binoculars: five professional researchers, including T. Masaki, the main author of this manuscript, and S. Koike, the co-author; three graduate students, including A. Nakajima, the main author of this manuscript; and three undergraduate students. Each of the 45 trees was assessed when its fruits were considered ripe in terms of color and size. Observers stood outside the edge of the tree crown, scanned the crown using binoculars, and counted the number of fruits using tally counters and cooking timers. The crowns of Q. crispula and Q. serrata, which have a large area relative to fruit size, were scanned for 30 s to reduce false-negative errors. The other six species, which have relatively smaller crown areas and/or have more easily visible fruits, were scanned for 10 s or 15 s to reduce false-positive errors. Two to four observers counted each focal tree three to five times. The combination of observers was randomly shuffled approximately every five trees.
2.4. Seed Trap Survey
On the same day the visual survey of a tree took place, seed traps with an opening size of 0.5 m2 were set beneath the scanned tree crown. To take into account the different tree crown area sizes, three traps were set for P. verecunda, Co. controversa, Q. crispula, and Q. serrata, while two traps were set for P. grayana, G. innovans, and S. commixta. After all the fruits had fallen (mostly by mid-December), the trap contents were retrieved. After sorting the contents, the number of Q. crispula and Q. serrata cupules and P. verecunda pedicels were counted, instead of the fruits. This was necessary to avoid underestimating or overestimating the number of fallen fruits, because fruits may be removed from the crown by birds, or fruits transported from other mother trees may be included in the traps also by birds. For P. grayana, Co. controversa, G. innovans, and S. commixta, the number of peduncles were counted. For Ca. crenata, three 0.5 m2 frames were randomly placed on the ground beneath the crown and counted the number of cupules inside the frame after all the cupules had fallen.
3. Analysis
3.1. Models and Inference
A simple power function was assumed between fruit density (i.e., the number of fallen
fruits per m2) (F) and the counts using binoculars, per observer and
per unit of time (1 s) (C) as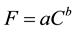 . The value of parameter a indi- cates the difficulty in finding
a fruit, and the value of parameter b roughly indicates the three-dimensional distribution
pattern of fruits within a crown. Log-transformation of this equation with indicators
produces the following:
. The value of parameter a indi- cates the difficulty in finding
a fruit, and the value of parameter b roughly indicates the three-dimensional distribution
pattern of fruits within a crown. Log-transformation of this equation with indicators
produces the following:
Table 1. List of studied species, with mean diameter at breast height (DBH) and its standard deviation in parentheses, approximate height, number of samples, study site, study year, observation unit, and its mean width (range in parentheses).
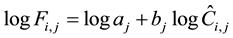 (1)
(1)
where Fi,j is true fruit density (m−2) of i-th
tree of species j and
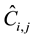 is the expected count per unit time (s−1) per observer scanning the tree
using a binocular. Their quantities are unknown. The aj and bj
parameters for species j are also unknown.
is the expected count per unit time (s−1) per observer scanning the tree
using a binocular. Their quantities are unknown. The aj and bj
parameters for species j are also unknown.
The number of fruits found in a trap, and the counts per observer, are modeled using the Poisson distribution:
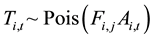 (2)
(2)
 (3)
(3)
where Ti,t is the number of fruits retrieved from t-th trap set beneath the i-th tree, Ai,t is the area of the trap or fame used, Ci,k is the counts by the observer k for the tree, and Si is the length of time (s) scanning the tree.
To estimate the parameters log aj and bj, a hierarchical Bayesian framework was used. The distributions of these parameters were modeled using hyper-parameters as follows:
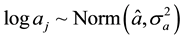 (4)
(4)
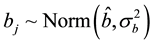 (5)
(5)
The noninformative priors for these parameters were provided by a uniform distribution:
from 0 to 100 for
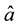 and
and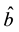 , and from
0 to 10,000 for
, and from
0 to 10,000 for
 and
and . The model
composed by the equations (1) to (5) is denoted as Model A.
. The model
composed by the equations (1) to (5) is denoted as Model A.
Following this, Model A was expanded to include observation errors depending on the observers. First, a relative value for each observer was evaluated. The value for the standard observer (A. Nakajima) was fixed at zero, whereas the values for the other observers were assumed to vary around zero. Thus, an observer finding more fruits (caused by a superior ability to find fruits or by false-positive errors resulting from an inferior ability) will get more counts than other observers and vice-versa. Based on this assumption, a supplemental equation was provided as follows:
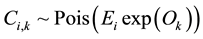 (6)
(6)
where Ok is the unique value for observer k, and Ei is the expected number of counts for the i-th tree by the standard observer. Both of these parameters are unknown. The noninformative prior of Ei was assumed as a uniform distribution ranging from 0 to 1,000, and that of Ok was a normal distribution with mean = 0 and standard deviation = 10,000. The equation (3) of Model A was then expanded to include the variation among observers:
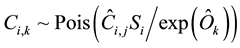 (7)
(7)
where
 is the mean of the posterior estimated for Ok. The model composed by
the Equations (1), (2), and (4) to (7) is denoted as Model B, which takes into consideration
the observer’s errors when counting the fruits.
is the mean of the posterior estimated for Ok. The model composed by
the Equations (1), (2), and (4) to (7) is denoted as Model B, which takes into consideration
the observer’s errors when counting the fruits.
To estimate the parameters of Models A and B, the MCMC method was used with Win BUGS ver. 1.4.3 (Spiegelhalter et al., 2003) . After several trials, the number of iterations was set to 55,000, and the first 5000 steps were discarded as burn-in. The remaining 50,000 steps were sampled every 10 steps (for a total of 5000 samplings) to generate a posterior distribution of each parameter. MCMC was conducted three times with randomly generated initial values for the parameters set for each chain. Based on visual assessments of the three chains, MCMC converged well and the Gelman-Rubin diagnostic for convergence assessment (Gelman et al., 2003) ranged from 1.00 to 1.08.
To check whether considering observer errors improves the accuracy of the model,
the expected values relative to the observed values were compared. Using the expected
( , the calculated
, the calculated

mean number of counts to the estimated model) and the observed (


3.2. Model Validation
The robustness of the inferred models was tested as follows: In the MCMC procedure, one tree in the data set was excluded from the analysis, and the parameters were estimated using the data of the remaining 44 trees. By applying the estimated parameters corresponding to the species of the unused tree, the expected fallen fruit density of the tree was calculated and compared with the value observed using the seed traps. When calculating the expected value, parameters a and b were randomly generated 10,000 times by referring to their posteriors, and the mean and 95% percentiles of 10,000 calculated values were used as the expected fruit density. The observed fallen fruit density was also represented using the mean and 95% percentiles, assuming that the numbers in the traps followed a Poisson distribution. If the 95% percentiles of the expected and observed values overlapped, the inferred model was considered robust. This procedure was implemented for each of the 45 trees.
4. Results
The number of counts/s, using binoculars, for 45 trees (8 species) by the 11 observers
(a few observers per tree) provided 535 values with a mean of 0.65 counts/s ranging
from 0.0 to 3.2 counts/s. The estimated values for

The studied species were roughly categorized into two groups, based on the estimated values of the two parameters, particularly a (Figure 2 and Table 2). Quercus and Prunus species had high a values (80 - 200), whereas the other species had less than 20. The estimated values of parameter b varied around 1.0 with an exceptionally greater value (approximately 2) for S. commixta. The estimated a values were highly correlated with the width of the observation unit (Figure 3). On the other hand, no significant correlation was found between b and the width of the observation unit.
Figure 4 shows the fitted results for Model A. All species, except S. commixta, appeared well-fit to the expected values. The validation also suggested that the estimated models were mostly robust, except for S. commixta (Figure 5): four of the six trees of S. commixta had significantly large differences between the expected and observed values. Some trees of Q. crispula also showed a significant difference for the lower range of fallen seed density. The other species showed more similar expected and observed values with insignificant differences.
Figure 1. Estimated values unique to the observers are shown by circles, triangles, and inverted triangles, corresponding to professional researchers, graduate students, and undergraduate students, respectively. The standard observer (A. Nakajima, author of this manuscript) is shown with an open symbol. Vertical bars show 95% credible intervals of the estimated posteriors.
Figure 2. Species distribution in relation to the estimates of parameters a and b. Solid circles show mean values, and horizontal and vertical bars represent 95% credible intervals of estimated posteriors. See Table 1 for abbreviations of species.
Figure 3. The parameter a as a function of the width of the observation unit (see Table 1). Vertical bars represent 95% credible intervals of the posteriors, and horizontal bars represent the range of unit width. The curve shows the fitted power function.
Table 2. Mean, standard
deviation (SD), 95% credible intervals of parameters a and b for the posterior of
each species are summarized (Model A). Gelman-Rubin diagnostics for convergence
assessment (
Figure 4. Fitted results of Model A for each species. Horizontal axes represent the number of counts of fruits per second using binoculars for each tree, averaged across multiple observers. The solid lines represent the estimated mean values of parameters a and b. For each species, 10,000 pairs of a and b values were randomly generated by referring to their posteriors, and the fruit density was calculated for each value along the x-axis, ranging from 0 to the specific maximum number of counts (1000 division). Dashed lines and vertical bars represent 95% confidence intervals of the estimated and observed fallen fruit density, respectively.
5. Discussion
This study provides three main findings. First, the number of fruits (or cupules and infructescences) per unit crown projection area of a tree can be accurately estimated by VSM, across multiple taxa, using species-specific parameters. Second, the species-specific parameter a decreases as a negative power function of the size of the unit to be observed. Using this relationship, VSM can be used for any tree taxa after examining their unit size. Third, the variation among observers did not substantially diminish the precision of the estimates. In the subsequent text, these findings were discussed in the context of using this method in the field.
Figure 5. Comparison between the expected and observed fallen fruit density. The dashed line shows the isoline. A larger symbol suggests that there is no significant difference between the expected and observed densities, and a smaller symbol suggests that they differ significantly. See Table 1 for abbreviations of species.
Figure 4 shows that the density of fruits (or cupules and infructescences) was estimated with reliable precision by VSM. For the seven species other than S. commixta, the predicted values fitted well with the observed values, almost as in a linear function. This is in accordance with the results obtained in previous studies with Fagaceae (Koenig et al., 1994; Perry & Thill, 1999; Giovanni et al., 2009) .
The crown area of a tree can be estimated from its diameter, or basal area, using a species-specific power function (see Appendix). Even in the case where the specific relationship between diameter and crown area is unknown, ecological or taxonomical information about the species may be helpful. A previous study revealed a correlation between shade tolerance and the power coefficient associated with diameter at breast height (DBH), when estimating the crown width (Russell & Weiskittel, 2011) . Therefore, parameters of the power function of a species’ crown size-diameter relationship may be inferred based on the tree shade tolerance class. More specifically, Gering & May (1995) grouped trees as coniferous or hardwood and developed group-specific equations for estimating tree crown width using DBH.
VSM developed in this study can be generalized and applied to any species. The parameter
a, which indicates the difficulty in finding a fruit, was clearly negatively associated
with the width of the observation unit (Figure 3),
and well regressed using the power function
In this study, parameter b had values around 1.0. Previous studies also found similar relationships between the number of fruits counted by VSM and the fallen seed density measured using seed traps (Koenig et al., 1994; Perry & Thill, 1999; Giovanni et al., 2009) . The value 1.0 for parameter b should have versatility. Therefore, when the species’ b values are unknown, it is recommended to use 1.0. On the other hand, the estimated b values varied between 0.62 and 1.47 among the species (except for S. commixta). Although any causes were identified for this interspecific variation, the bias due to this variation was not considered relevant, as explained below. In this study, the maximum number of counts/s was 3.2. Assuming that a is set to 30 (average value; see Figure 2), and b is set to0.62, 1.47, or 1.0, the fallen fruit densities corresponding to the count number of 3.2 would be 61.7, 165.8, and 96.0, respectively. The biases relative to the calculation with b = 1.0 are neither more than twofold (1.73) nor less than half (0.64).
It was also shown that any errors due to the observers did not cause a serious bias
in the estimation with VSM. Of the 11 observers who participated in VSM of this
study, only two showed significantly lower

Among the species examined in this study, only S. commixta appeared as an outlier (Figures 2-4). The size (mean DBH and height) of this species’ sample trees was the smallest among those examined in this study (Table 1). Such a low tree height may not be suitable for VSM because the visible area in a binocular becomes narrow and likely results in false-positive errors. The data for S. commixta in Figure 4 show that the fruiting density was almost zero even when the number of counts was moderate; this is an evidence of a false-positive error. Therefore, VSM may not be a good method to estimate the crop size of small size trees.
6. Conclusion
For the sustainable management of natural forests, it is crucial to estimate the tree crop size prior to regeneration treatments. From the perspective of wildlife management, it is essential for better management to estimate fruit production across various species, and over a wide range of habitat, as early as possible (Inman & Pelton, 2002; Nakajima, 2015) . Under these needs, the generalized VSM presented in this study has advantages in terms of low workload as well as precision and robustness.
Acknowledgements
The authors sincerely thank late Dr. Nobuo Kanzaki and late Dr. Tatsuro Kanazashi for their encouragement; Dr. Shin Abe, Dr. Shoji Naoe, Dr. Masataka Ohashi, Dr. Takayuki Ota, Ms. Ayako Sawa Matsuki, Ms. Akiko Fujitsu, Mr. Takashi Ikeda, and Ms. Yuko Kamite for helping with the field work; and colleagues in the laboratory for supporting our work. This study was partly funded by the Ministry of the Environment, Japan (The study project on the Japanese black bears’ mass intrusion into human settlements), Grant-in-Aid for Young Scientists (B) (22780141), Grant-in-Aid for JSPS Fellows (22-7646), and JSPS KAKENHI (Grant Number 25241026).
Cite this paper
AmiNakajima,TakashiMasaki,ShinsukeKoike,KojiYamazaki,KoichiKaji,11, (2015) Estimation of Tree Crop Size across Multiple Taxa: Generalization of a Visual Survey Method. Open Journal of Forestry,05,651-661. doi: 10.4236/ojf.2015.57057
References
- 1. Bechtold, W. A. (2003). Crown-Diameter Prediction Models for 87 Species of Stand-Grown Trees in the Eastern United States. Southern Journal of Applied Forestry, 27, 269-278.
- 2. Carevic, F. S., Alejano, R., Fernández, M., &
Martín, D. (2014). Assessment and Comparison of the Visual Survey Method
for Estimating Acorn Production in Holm Oak (Quercus ilex ssp. ballota) Open Woodland
of Southwestern Spain. Arid Land Research and Management, 28, 102-108.
http://dx.doi.org/10.1080/15324982.2013.808718 - 3. Condés, S., & Sterba, H. (2005). Derivation of
Compatible Crown Width Equations for Some Important Tree Species of Spain. Forest
Ecology and Management, 217, 203-218.
http://dx.doi.org/10.1016/j.foreco.2005.06.002 - 4. Gelman, A., Carlin, J. B., Stern, H. S., & Rubin, D. B. (2003). Bayesian Data Analysis (2nd ed.). London: Champan and Hall/CRC.
- 5. Gering, L. R., & May, D. M. (1995). The Relationship of Diameter at Breast Height and Crown Diameter for Four Species Groups in Hardin County, Tennessee. Southern Journal of Applied Forestry, 19, 177-181.
- 6. Gill, S. J., Biging, G. S., & Murphy, E. C. (2000). Modeling
Conifer Tree Crown Radius and Estimating Canopy Cover. Forest Ecology and Management,
126, 405-416.
http://dx.doi.org/10.1016/S0378-1127(99)00113-9 - 7. Giovanni, P., Marzia, M., Marco, P., Luciano, S., Tiziana, A., Mario, P., Mario, R., & Marco, C. (2009). Monitoring Brown Bear (Ursusarctos) Critical Food Resources in Beech (Fagus sylvatica) Forest: Beechnut Production in the Central Apennines, Italy. Proceedings of the XXIII World Forestry Congress, Buenos Aires, 18-23 October 2009, 18-25.
- 8. Inman, R. M., & Pelton, M. R. (2002). Energetic Production by Soft and Hard Mast Foods of American Black Bears in the Smoky Mountains. Ursus, 13, 57-68.
- 9. Kitamura, S., & Murata, G. (1971). Colored Illustrations of Woody Plants of Japan I. Osaka: Hoikusya. (In Japanese)
- 10. Kitamura, S., & Murata, G. (1979). Colored Illustrations of Woody Plants of Japan II. Osaka: Hoikusya. (In Japanese)
- 11. Koenig, W. D., Knops, J. M. H., Carmen, W. J., Stanback,
M. T., & Mumme, R. L. (1994). Estimating Acorn Crops Using Visual Surveys. Canadian
Journal of Forest Research, 24, 2105-2112.
http://dx.doi.org/10.1139/x94-270 - 12. Koike, S., & Masaki, T. (2008). Frugivory of Carnivora
in Central and Southern Parts of Japan Analyzed by Literature Search. Journal of
Japanese Forestry Society, 90, 26-35.
http://dx.doi.org/10.4005/jjfs.90.26 - 13. Masaki, T., & Abe, S. (2008). A Test of Visual Assessment
of Crop Size of Quercus crispula Using a Binocular. Journal of Japanese Forestry
Society, 90, 241-246.
http://dx.doi.org/10.4005/jjfs.90.241 - 14. Masaki, T., Oka, T., Osumi, K., & Suzuki, W. (2008).
Geographical Variation in Climatic Cues for Mast Seeding of Fagus crenata. Population
Ecology, 50, 357-366.
http://dx.doi.org/10.1007/s10144-008-0104-6 - 15. Masaki, T., Suzuki, W., Niiyama, K., Iida, S., Tanaka, H.,
& Nakashizuka, T. (1992). Community Structure of a Species-Rich Temperate Forest,
Ogawa Forest Reserve, Central Japan. Vegetation, 98, 97-111.
http://dx.doi.org/10.1007/BF00045549 - 16. Masaki, T., Takahashi, K., Sawa, A., Kado, T., Naoe, S.,
Koike, S., & Shibata, M. (2012). Fleshy Fruit Characteristics in a Temperate
Deciduous Forest of Japan: How Unique Are They? Journal of Plant Research, 125,
103-114.
http://dx.doi.org/10.1007/s10265-011-0423-0 - 17. Mogi, T., Katsuyama, T., Ota, K., Sakio, H., Takahashi, H., Ishii, H., Kigawa, S., & Nakagawa, S. (2000). Flowers Bloom in Woody Plants 1. Tokyo: Yamatokeikoku-sya. (In Japanese)
- 18. Nakajima, A., Koike, S., Masaki, T., Shimada, T., Kozakai,
C., Nemoto, Y., Yamazaki, K., & Kaji, K. (2012). Spatial and Elevational Variation
in Fruiting Phenology of a Deciduous Oak and Foraging Behavior of Asiatic Black
Bear (Ursusthibetanus). Ecological Research, 27, 529-538.
http://dx.doi.org/10.1007/s11284-011-0919-z - 19. Nakajima, H. (2015). Estimating Sound Seedfall Density of
Fagus crenata Using a Visual Survey. Journal of Forest Research, 20, 94-103.
http://dx.doi.org/10.1007/s10310-014-0440-7 - 20. Nakashizuka, T., & Matsumoto, Y. (2002). Diversity and
Interaction in a Temperate Forest Community. Tokyo: Springer.
http://dx.doi.org/10.1007/978-4-431-67879-3 - 21. Noyce, K. V., & Coy, P. L. (1990). Abundance and Productivity of Bear Food Species in Different Forest Types of Northcentral Minnesota. Bears: Their Biology and Management, 8, 169-181.
- 22. Perry, R. W., & Thill, R. E. (1999). Estimating Mast Production: An Evaluation of Visual Surveys and Comparison with Seed Traps Using White Oaks. Southern Journal of Applied Forestry, 23, 164-169.
- 23. Russell, M. B., & Weiskittel, A. R. (2011). Maximum and Largest Crown Width Equations for 15 Tree Species in Maine. Northern Journal of Applied Forestry, 28, 84-91.
- 24. Satake, Y., Hara, H., Watari, S., & Tominari, T. (1999a). Wild Flowers of Japan. Woody Plants I. Tokyo: Heibonsha. (In Japanese)
- 25. Satake, Y., Hara, H., Watari, S., & Tominari, T. (1999b). Wild Flowers of Japan. Woody plants II. Tokyo: Heibonsha. (In Japanese)
- 26. Spiegelhalter, D. J., Thomas, A., Best, N. G., & Lunn, D. (2003). WinBUGS Version 1.4 User Manual. Cambridge: MRC Biostatistics Unit.
- 27. Tsuji, Y., Fujita, S., Sugiura, H., Saito, C., & Takatsuki,
S. (2006). Long-Term Variation in Fruiting and the Food Habits of Wild Japanese
Macaques on Kinkazan Island, Northern Japan. American Journal of Primatology, 68,
1068-1080.
http://dx.doi.org/10.1002/ajp.20307
Appendix: Basal Area-Crown Area Relationships
The basal area (BA) and tree crown area (CA) of 41 of the 45 trees in this study (some missing data for Quercus crispula and Castanea crenata) were measured. BA was used instead of diameter because some trees had multi-stems, and summed BAs of constituent stems were better representatives of individuals. The BA of each stem was calculated from the girth of the tree trunk at 1.2-m height, measured to the nearest 0.1 cm. The CA of an individual tree was estimated by measuring the radius of the crown in eight directions and calculating the crown area as an octagon. The compass direction of one radius was randomly selected, and the second was computed at 45° to the first, and so on. Each radius was measured to the nearest 0.1 m. Then, the following equation was set:
where, ci,j and bi,j are CA and BA of
i-th tree of species j, respectively, αj and βj are unknown
parameters for species j, and







The estimated results are summarized in Table 1A. The fitting result shown in Figure 1A suggests that specific power functions are useful to estimate crown projection areas from the basal area.
Figure 1A. Crown projection areas as a function of basal area. Solid lines represent fitted results.
Table 1A. Estimated parameters for power functions between basal area and crown projection areas.
NOTES
*Top authors.












