Open Journal of Acoustics
Vol.05 No.04(2015), Article ID:61701,19 pages
10.4236/oja.2015.54013
A Study on the Linear Piezoelectric Motor of Mode Shape
Jwo Ming Jou
Department of Mechanical Engineering, Cheng Shiu University, Taiwan

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 1 October 2015; accepted 1 December 2015; published 4 December 2015

ABSTRACT
In this paper, we want to make a new type linear piezoelectric motor by mode shape coating or effective electrode surface coating. The mode shape is derived from the mechanical boundary conditions of the linear piezoelectric motor. We only have access to the first three modes of formas, the effective electrode surface coating basis, as well as with the linear piezoelectric motor of normal shape do comparison. Next, we will inspect their gain or axial velocity through theoretical analysis, simulation and experiment. According to the results of the theoretical analysis, we have found that the gain or axial velocity of the linear piezoelectric motors of mode shape is much larger than the linear piezoelectric motors of normal shape. However, according to the results of simulation and experiments, we have found that the gain or axial velocity of the linear piezoelectric motors of mode shape is much greater than the linear piezoelectric motors of normal shape, which is about 1.2 to 1.4 times. The linear piezoelectric motor of mode shape 3 has the fastest axial velocity, which is about −48 mm/s and 48 mm/s under conditions of 180 Vp−p driving voltage, 21.2 kHz driving frequency (the third vibration modal), 25 gw loading and the position of loading or mass at x = 5 mm & 45 mm respectively. And its axial velocity is about 1.4 times the linear piezoelectric motor of normal shape under the same conditions. Overall, the mode shape coating helps to enhance the gain or axial velocity of the linear piezoelectric motor.
Keywords:
Linear Piezoelectric Motor (LPM), Mode Shape (MS), Normal Shape (NS), Gain, Axial Velocity

1. Introduction
Over the past decade, the linear piezoelectric motors have a very significant development and excellent performance, as shown in Table 1 [1] -[19] . If we do not consider the size and the driving condition of the piezoelectric linear motors, their linear moving fastest is a high-power linear ultrasonic motor using bending vibration
Table 1. The performance comparison of the linear piezoelectric motors [1] -[19] .
transducer [15] , the ultrasonic linear motor using traveling surface acoustic wave [6] and a linear ultrasonic motor using push-pull type L-B hybrid Langevin transducer with single foot [3] . Their linear movement speed of the fastest are 1527 mm/s, 1500 mm/s and 1280 mm/s respectively. If we only pay attention to thrust or loading ability, such as the square matrix type ultrasonic motor [7] , a 2-DOF planar ultrasonic motor using longitudinal- bending hybrid transducer [5] and aultrasonic linear motor using longitudinal and bending multimode bolt- clamped Langevin type transducer [1] have the best performance. Their maximum thrust or loading are 142N, 103N and 100N respectively. If it focuses on energy efficiency, they are a linear piezoelectric motor driven by a single-phase signal [12] , a multimode ultrasonic motor [10] and an ultrasonic linear motor using traveling surface acoustic wave [6] . Their minimum driving voltages are 16 Vp−p, 30 Vp−p and 80 Vp−p respectively. Due to the linear piezoelectric motors have superior performance, and they have a high use value in the precision mechanical systems. So in addition to the above the linear piezoelectric motors, in any form or performance of the linear piezoelectric motors are worth trying to develop. In addition, we, according to the rotary piezoelectric motor of mode shape, have the advantage of a high rotational speed and excellent performance [20] . We try to use the same mode shape coating method to produce a new linear piezoelectric motor, and hope the linear piezoelectric motor of mode shape also have a more superior performance with respect to the linear piezoelectric motor using normal shape coating, which is our motivation and main purpose in this paper.
2. The Function of Mode Shape and Effective Electrode Surface
In this study, the linear piezoelectric motor can be regarded as a like simple supported beam with pinned-pinned boundary conditions [20] [21] , shown in Figure 1. So we can get the origin function of mode shape 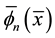 of the linear piezoelectric motor as follows:
of the linear piezoelectric motor as follows:
Figure 1. The origin functions of mode shape of the linear piezoelectric motors under pinned-pinned boundary conditions.
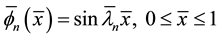 . (1)
. (1)
where the dimensionless eigenvalues 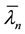 is defined as:
is defined as:
 (2)
(2)
And further we can get another function of the effective electrode surface 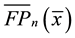 from Equation (1) as follows or shown in Figure 2 and Table 2:
from Equation (1) as follows or shown in Figure 2 and Table 2:
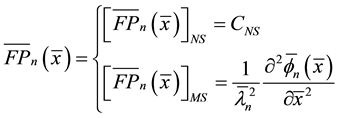 . (3)
. (3)
where the 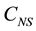 is defined as a constant. The subscript of NS and MS represent normal shape and mode shape.
is defined as a constant. The subscript of NS and MS represent normal shape and mode shape.
Figure 2. The first three functions of mode shape and the effective electrode surface of the linear piezoelectric motors.
Table 2. The first three vibration modes and effective electrode surfaces of the mode shape piezoelectric ceramics under pinned-pinned boundary conditions.
3. The Composition and Operation Principle
According to the functions of the effective electrode surface or from Equation (3), we can design a series of linear piezoelectric motors, including the linear piezoelectric motors of normal shape and mode shape, as shown in Figure 3. For the linear piezoelectric motors of mode shape, we just take the first three functions of the mode shape and the effective electrode surface as the subject of research. As for the main components of the linear piezoelectric motor comprise two piezoelectric ceramics and an aluminum base of bench type. Which the polarization directions of the two piezoelectric ceramics are in pairs. When we operate the linear piezoelectric motor, only applied driving voltage (V3) and resonance frequency (fr) or proper loading, we can make linear motion of the piezoelectric motor, as shown in Figure 4. When the right membrane force is greater than the left side of the
Figure 3. The composition of the linear piezoelectric motors of normal shape and mode shape.
Figure 4. The operation principle and motion state of the linear piezoelectric motor of normal shape or mode shape.
membrane force, the piezoelectric motor will move to the right. On the contrary, the piezoelectric motor will then move to the left.
4. The Equations of Axial and Transverse Vibration
In order to distinguish differences of the linear piezoelectric motor of the normal shape and mode shape, we can simplify the equations of motion of 3D structure into the equation of motion of the two 1D structures. One of which is the equation of motion of the axial vibration direction, the other is the equation of motion of the transverse vibration direction as follow:
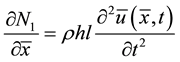 , (4)
, (4)
and
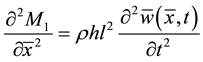 , (5)
, (5)
where the membrane force (N1) and of bending moment (M1) unit width are defined as:

and

We can let Equation (1)-(3) & (6) (7) are substituted into Equation (4) & (5), and then after finishing, we can get the equations of motion by axial and transverse displacement of the linear piezoelectric motor of the normal shape and mode shape as follow:


and


According above the Equations (8)-(11), we can get the general solutions of axial and transverse vibration displacement (


and


where the definition of constants or symbols in the above Equations (4)-(15) as follow:









where in above the symbols of A11, An, c11, D11, e31, fi, fn, h, t, U, u, V3, W, w, x, z, ρ, ωi, ωn, 



Where above undetermined coefficients can be determined by the following electro-mechanical boundary conditions:


and


where


and


Another the frictional force is defined as follow:

where 


Because the functions of mode shape are equal to zero under pinned-pinned boundary conditions as:

So the Equation (30) and Equation (32) can be rewritten as follows:

and

where

Let Equations (25)-(36) are substituted into Equations (12)-(15), we can get the solution of the axial and transverse vibration displacement of the first three modes of the linear piezoelectric motors as follow:


and


Let Equations (35)-(41) are substituted into Equations (12)-(15), we can get the particular solutions of the transverse and axial vibration displacement of the linear piezoelectric motor as follow:


and


Further, we can make Equations (42)-(45) simplified as follows:


and


where 
Therefore, we can once again get the equations of elliptical trajectory of the linear piezoelectric motor of normal shape and mode shape at contact points on both sides from above Equations (46)-(49), as follow or shown in Figure 4:

and

At this point we can see the difference in the linear motors of normal shape and mode shape from the solutions of displacement. Then we will be to test their differences or gains by the case study of theoretical analysis, computer simulation and experiments.
5. Special Case Study of Theoretical Analysis, Simulation Analysis and Experiments
We have to understand the differences and gain between the linear piezoelectric motors of the normal shape and mode shape in this study. We will try to verify the differences and gain of the linear piezoelectric motors through theoretical analysis, simulation analysis and experiments. Where in the associated electrical and mechanical properties of the linear piezoelectric motors in special case study is shown in Table 3.
The first is theoretical analysis in this special case study, which is as follows:
(5-1-1) Try to find the approximate solution of the transverse displacement of the linear piezoelectric motors of the normal shape and mode shape in the special case study. We can take to understand their difference and gain under condition of the normal shape and different mode shape electrode coating.
(5-1-2) Try to find the approximate solution of the axial displacement of the linear piezoelectric motors of the normal shape and mode shape in the special case study. We can further understand the impact of the axial or linear movement under conditions of the normal shape and different mode shape electrode coating or the above modal vibration.
(5-1-3) Try to understand the impact of the axial or linear movement of the linear piezoelectric motors of the normal shape and mode shape under conditions of the different loading (or mass) and positions.
Second is simulation analysis by ANSYS code (its modal analysis under different driving conditions shown in Figures 5-10, its main analytical work as follows:
(5-2-1) Try to find the vibration modal of the linear piezoelectric motors of the normal shape and mode shape in the special case study.
(5-2-2) Try to find the axial (or linear) and transverse displacement from the above vibration modal under condition of net weight.
(5-2-3) Try to find the axial (or linear) and transverse displacement under conditions of different loading, position and steady state.
(5-3-1) Finally the experimental work (its prototype and structure shown in Figure 11, Figure 12 as follows:
(5-3-2) Try to find the maximum axial (or linear) speed of linear piezoelectric motors of the normal shape and mode shape under condition of net weight.
(5-3-3) Try to find the maximum axial (or linear) speed of linear piezoelectric motors of the normal shape and mode shape under condition of the different loading (or mass) and position.
6. Results and Discussion
According to the results of theoretical analysis, simulation analysis and experiments, we found:
1) Shown in Figures 13-15, we have found that the change in axial displacement or velocity of more focus and smooth of the linear piezoelectric motors of mode shape with respect to the linear piezoelectric motor of normal shape by theoretical analysis under conditions of the first three vibration modal or driving frequency, 180 Vp−p driving voltage, net weight, frequency spacing of 1 Hz and the first three eigenvalues.
2) Shown in Figure 16, we have found that the gain in transverse displacement or velocity of the linear piezoelectric motors of mode shape is much larger than the linear piezoelectric motor of normal shape by theoretical analysis under conditions of the first three vibration modal or driving frequency, 180 Vp−p driving voltage, net weight, frequency spacing of 1 Hz and the first three eigenvalues.
Table 3. The material properties and size of the linear piezoelectric motor.
Figure 5. The first modal analysis of the linear piezoelectric motors of mode shape 1 under 180 Vp−p, 17 gw net weight and pinned-pinned boundary conditions.
Figure 6. The second modal analysis of the linear piezoelectric motors of mode shape 1 under 180 Vp−p, 17 gw net weight and pinned-pinned boundary conditions.
Figure 7. The third modal analysis of the linear piezoelectric motors of mode shape 1 under 180 Vp−p, 17 gw net weight and pinned-pinned boundary conditions.
Figure 8. The first modal analysis of the linear piezoelectric motors of mode shape 1 under 180 Vp−p, 25 gw loading, the position of loading at x = 5 mm and pinned-pinned boundary conditions.
Figure 9. The second modal analysis of the linear piezoelectric motors of mode shape 1 under 180 Vp−p, 25 gw loading, the position of loading at x = 5 mm and pinned-pinned boundary conditions.
Figure 10. The third modal analysis of the linear piezoelectric motors of mode shape 1 under 180 Vp−p, 25 gw loading, the position of loading at x = 5 mm and pinned-pinned boundary conditions.
Figure 11. The prototype of the linear piezoelectric motors of normal shape and mode shape.
Figure 12. The experimental structure of the linear piezoelectric motors of normal shape and mode shape.
Figure 13. The dimensionless axial displacement or velocity relative to the dimensionless length of the linear piezoelectric motors of the normal shape and mode shape by theoretical analysis under conditions of the first vibration modal, 180 Vp−p driving voltage, 17 gw net weight, frequency spacing of 1 Hz, eigenvalues of λ1 and β1.
Figure 14. The dimensionless axial displacement or velocity relative to the dimensionless length of the linear piezoelectric motors of the normal shape and mode shape by theoretical analysis under conditions of the first vibration modal, 180 Vp−p driving voltage, 17 gw net weight, frequency spacing of 1 Hz, eigenvalues of λ2 and β2.
Figure 15. The dimensionless axial displacement or velocity relative to the dimensionless length of the linear piezoelectric motors of the normal shape and mode shape by theoretical analysis under conditions of the first vibration modal, 180 Vp−p driving voltage, 17 gw net weight, frequency spacing of 1 Hz, eigenvalues of λ3 and β3.
3) Shown in Figure 17, we have found that the gain in axial displacement or velocity of the linear piezoelectric motors of mode shape is much larger than the linear piezoelectric motor of normal shape by theoretical analysis under conditions of the first three vibration modal or driving frequency, 180 Vp−p driving voltage, different position of loading or mass, frequency spacing of 1 Hz and the first three eigenvalues.
4) Shown in Figure 18, we have found that the gain in axial displacement or velocity of the linear piezoelectric motors of mode shape is much slightly than the linear piezoelectric motor of normal shape by simulation analysis under conditions of different position of loading or mass, 180 Vp−p driving voltage, 25 gw loading and the first three vibration modal or driving frequency.
5) Shown in Table 4, the modal resonance frequency of the linear piezoelectric motors of normal shape and mode shape by 1D theoretical analysis, 3D simulation analysis and experiments, there are 2.14 kHz ~ 3.2 kHz, 8.56 kHz ~ 11.2 kHz and 19.26 kHz ~ 21.2 kHz respectively.
6) Shown in Figure 19, we have found that the gain in axial displacement or velocity of the linear piezoelectric motors of mode shape is much slightly than the linear piezoelectric motor of normal shape by experiments
Figure 16. The dimensionless transverse displacement or velocity relative to the dimensionless length of the linear piezoelectric motors of the normal shape and mode shape by theoretical analysis under conditions of the first three vibration modal, 180 Vp−p driving voltage, 17 gw net weight and frequency spacing of 1 Hz.
Figure 17. The dimensionless axial displacement or velocity relative to the position of loading or mass of the linear piezoelectric motors of the normal shape and mode shape by theoretical analysis under conditions of the frequency spacing of 1 Hz, 180 Vp−p driving voltage and the first three vibration modal.
Table 4. The modal resonance frequency of the linear piezoelectric motors of normal shape and mode shape by 1D theoretical analysis, 3D simulation analysis and experiments.
Figure 18. The dimensionless axial displacement or velocity relative to the position of loading or mass of the linear piezoelectric motors of the normal shape and mode shape by simulation analysis under conditions of 180 Vp−p driving voltage, 25 gw loading and the first three vibration modal.
Figure 19. The axial displacement velocity relative to the position of loading or mass of the linear piezoelectric motors of the normal shape and mode shape by experiments under conditions of 180 Vp−p driving voltage, 25 gw loading, and the driving frequency of the first three vibration modal.
under conditions of different position of loading or mass, 180 Vp−p driving voltage, 25 gw loading and the first three vibration modes or driving frequency. Wherein the linear piezoelectric motor of mode shape 3 having the fastest axial velocity, which is about −48 mm/s and 48 mm/s under conditions of 180 Vp−p driving voltage, 21.2 kHz driving frequency (the third vibration modal), 25 gw loading and the position of loading or mass at x = 5 mm & 45 mm respectively. And its axial velocity is about 1.4 times the linear piezoelectric motor of normal shape under the same conditions.
7. Conclusion
According to the results of theoretical analysis, simulation analysis and experiments, we have found that the change in axial displacement or velocity of the linear piezoelectric motors of mode shape is more focus and smooth than the linear piezoelectric motor of normal shape. We also have found that the gain in axial and transverse displacement or velocity of the linear piezoelectric motors of mode shape is much larger than the linear piezoelectric motor of normal shape. We have further found that the axial velocity of the linear piezoelectric motors of mode shape is much larger than the linear piezoelectric motor of normal shape under condition of eccentric loading or mass. We also have found that the linear piezoelectric motors of normal shape and mode shape cannot move faster, when the state of net weight or the loading (or mass) placed at the center position of the motors. When the loading or mass is farther away from the center, it’s moving faster. And we also have found that the placement of the loading or mass can change the direction of axial movement of the motors. Overall, for all motors, the gain of the axial velocity of the third vibration modal is much larger than the first and second vibration modal. From the above results, we have found that the transverse mode shape coating has a positive effect on the axial displacement. That is, the transverse mode shape coating can make energy more concentrated with respect to the normal shape coating, so that axial displacement can more quickly move.
Acknowledgements
This study can be finished smoothly, I especially want to thank MOST of Taiwan of ROC sponsor on funding, (Project No.: MOST104-2221-E-230-016).
Cite this paper
Jwo MingJou, (2015) A Study on the Linear Piezoelectric Motor of Mode Shape. Open Journal of Acoustics,05,153-171. doi: 10.4236/oja.2015.54013
References
- 1. Shi, S.J., Chen, W.S. and Liu, J.K. (2006) A High Speed Ultrasonic Linear Motor Using Longitudinal and Bending Multimode Bolt-Clamped Langevin Type Transducer. Proceedings of the 2006 IEEE International Conference on Mechatronics and Automation, Luoyang, 25-28 June 2006, 612-617.
- 2. Jou, J.M. and Hou, J.L. (2007) A Study on the New Type Linear Ultrasonic Motor. 2007 IEEE International Ultrasonic Symposium, New York, 28-31 October 2007, 2554-2557.
- 3. Shi, S.J., Chen, W.S., Liu, Y.X., Liu, J.K. and Xie, T. (2008) Design and Fabrication of a Linear Ultrasonic Motor Using Push-Pull Type L-B Hybrid Langevin Transducer with Single Foot. 2008 IEEE International Ultrasonics Symposium, Beijing, 2-5 November 2008, 157-160.
- 4. Yao, Z.Y., Yang, D., Wu, X. and Zhao, C.S. (2008) Structure Design Method of Bar-Structure Linear Ultrasonic Motors. 2008 IEEE International Ultrasonics Symposiums, Beijing, 2-5 November 2008, 639-642.
- 5. Shi, S.J., Liu, J.K., Chen, W.S. and Liu, Y.X. (2009) Development of a 2-DOF Planar Ultrasonic Motor Using Longitudinal-Bending Hybrid Transducer. 18th IEEE International Symposium on Applications of Ferroelectrics, Xian, 23-27 August 2009, 1-5.
- 6. Kurosawa, M.K. (2009) Ultrasonic Linear Motor Using Traveling Surface Acoustic Wave. 2009 IEEE International Ultrasonics Symposium, Rome, 19-23 September 2009, 1096-1105.
- 7. Jou, J.M., Kung, H.-K. and Huang, B.-W. (2009) A Study on the Square Matrix Type Ultrasonic Motor. 2009 International Symposium on Mechatronic and Biomedical Engineering & Applications, Taiwan, 5 November 2009, 247-252.
- 8. Liu, Y.X., Chen, W.S., Liu, J.K. and Shi, S.J. (2010) A High-Power Linear Ultrasonic Motor Using Longitudinal Vibration Transducers with Single Foot. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 57, 1860-1867.
- 9. Jou, J.-M. (2011) A Study on the Arch Type Ultrasonic Motor. International Conference on Electric Information and Control Engineering, ICEICE 2011, IEEE Publication, Jiangxi, 6-8 April 2011, 1123-1126.
- 10. Takasaki, M., Takano, H., Ji, H. and Mizuno, T. (2011) Modified Transducer for Multimode Ultrasonic Motor. IEEE/ ASME International Conference on Advanced Intelligent Mechatronics (AIM), Budapest, 3-7 July 2011, 623-628.
- 11. Liu, Y.X., Liu, J.K., Chen, W.S. and Shi, S.J. (2012) A U-Shaped Linear Ultrasonic Motor Using Longitudinal Vibration Transducers with Double Feet. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 59, 981-989.
http://dx.doi.org/10.1109/TUFFC.2012.2283 - 12. Liu, Y.X., Chen, W.S., Liu, J.K. and Shi, S.J. (2013) Analysis of a Linear Piezoelectric Motor Driven by a Single-Phase Signal. IEEE International Ultrasonics Symposium (IUS), Prague, 21-25 July 2013, 481-484.
- 13. Chen, Z.J., Li, X.T., Chen, J.G. and Dong, S.X. (2013) A Square-Plate Ultrasonic Linear Motor Operating in Two Orthogonal First Bending Modes. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 60, 115-120.
http://dx.doi.org/10.1109/TUFFC.2013.2543 - 14. Liu, Y.X., Chen, W.S., Liu, J.K. and Shi, S.J. (2013) A Rectangle-Type Linear Ultrasonic Motor Using Longitudinal Vibration Transducers with Four Driving Feet. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 60, 777-785.
http://dx.doi.org/10.1109/TUFFC.2013.2626 - 15. Liu, Y.X., Chen, W.S., Liu, J.K. and Yang, X.H. (2013) A High-Power Linear Ultrasonic Motor Using Bending Vibration Transducer. IEEE Transactions on Industrial Electronics, 60, 5160-5166.
http://dx.doi.org/10.1109/TIE.2012.2233691 - 16. Ci, P.H., Chen, Z.J., Liu, G.X. and Dong, S.X. (2014) A Square-Plate Piezoelectric Linear Motor Operating in Two Orthogonal and Isomorphic Face-Diagonal-Bending Modes. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 61, 159-165.
http://dx.doi.org/10.1109/TUFFC.2014.6689783 - 17. Zhou, S.L. and Yao, Z.Y. (2014) Design and Optimization of a Modal-Independent Linear Ultrasonic Motor. IEEE Transactions on Industrial Electronics, 61, 535-546.
http://dx.doi.org/10.1109/tuffc.2014.2937 - 18. Guo, M.S., Pan, S., Hu, J.H., Zhao, C.S. and Dong, S.X. (2014) A Small Linear Ultrasonic Motor Utilizing Longitudinal and Bending Modes of a Piezoelectric Tube. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 61, 705-709.
http://dx.doi.org/10.1109/TUFFC.2014.2958 - 19. Li, X.T., Ci, P.H., Liu, G.X. and Dong, S.X. (2015) A Two-Layer Linear Piezoelectric Micromotor. IEEE Transactions on Industrial Electronics, 62, 405-411.
http://dx.doi.org/10.1109/tuffc.2014.006796 - 20. Jou, J.-M. (2015) A Study on the Mode Shape Piezoelectric Motor. Open Journal of Acoustics, 5, 45-65.
http://dx.doi.org/10.4236/oja.2015.52005 - 21. Jou, J.-M. (2014) Theory and Simulation Analysis of the Mode Shape and Normal Shape Actuators and Sensors. Open Journal of Acoustics, 4, 184-203.
http://dx.doi.org/10.4236/oja.2014.44019






















