Open Journal of Acoustics
Vol.05 No.03(2015), Article ID:59370,14 pages
10.4236/oja.2015.53007
Dramatic Influence of the Magnetoelectric Effect on the Existence of the New SH-SAWs Propagating in Magnetoelectroelastic Composites
Aleksey Anatolievich Zakharenko
International Institute of Zakharenko Waves (IIZWs), Krasnoyarsk, Russia
Email: aazaaz@inbox.ru
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 July 2015; accepted 1 September 2015; published 4 September 2015
ABSTRACT
This comparative study acquaints the reader with some properties of the eighth and tenth new shear-horizontal surface acoustic waves (SH-SAWs) propagating along the free surface of the magnetoelectroelastic (6 mm) medium. These new nondispersive SH-SAWs cannot exist when the electromagnetic constant α is equal to zero. The piezoelectromagnetic SH bulk acoustic wave and the surface Bleustein-Gulyaev-Melkumyan (BGM) wave are also chosen for comparison. The main problem of this report is the demonstration of the fact that the new waves can propagate slower than the BGM wave. This problem can be very important due to the fact that among the other known SH-SAWs the BGM wave can propagate significantly slower than the corresponding SH bulk acoustic wave. Two new SH-SAWs are analytically and graphically studied in dependence on the electromagnetic constant α. For the graphical study, two (6 mm) composites are used: BaTiO3? CoFe2O4 and PZT-5H?Terfenol-D. For the second composite it is solidly demonstrated that for small values of α, the eighth new SH-SAW cannot exist and its velocity starts with zero at some small threshold value of α rapidly reaching the BGM-wave velocity. This means that a weak magnetoelectric effect can dramatically slow down the speed of either new SH-SAW. As a result, the studied new SH-SAWs can be suitable for creation of new technical devices to sense the magnetoelectric effect. For the analytical study, extreme and inflexion points were evaluated in the velocities’ dependencies on the value of the electromagnetic constant α.
Keywords:
Magnetoelectroelastics, Magnetoelectric Effect, New SH-SAW, Bleustein-Gulyaev-Melkumyan Wave

1. Introduction
Two researchers, Bleustein [1] and Gulyaev [2] , are responsible for the creation of new knowledge because they have discovered the surface Bleustein-Gulyaev (BG) waves to the end of the 1960s. The researchers have theoretically studied the acoustic wave propagation along the surface of a piezoelectric (PE) 6 mm solid when the shear-horizontal surface acoustic wave (SH-SAW) propagates perpendicular to and is polarized along the sixfold symmetry axis [3] . The slower BG-wave possesses an important feature such as its velocity can be significantly slower than the corresponding shear-horizontal bulk acoustic wave (SH-BAW). The difference between the surface BG-wave and SH-BAW velocities illuminates the following fact: the stronger the piezoelectric effect is, the larger the difference and smaller the penetration depth would be. This is also true for the transversely isotropic (6 mm) piezomagnetics (PM) that can also support the piezomagnetic BG-wave propagation.
In addition to the PE and PM solids there are piezoelectromagnetic (PEM) continua, also known as magnetoelectroelastics. The SAW peculiarities mentioned above for the PEs and PMs are also true for the PEMs. In the 6 mm PEM continua, the surface Bleustein-Gulyaev-Melkumyan (BGM) wave can propagate. The BGM wave was recently discovered by Melkumyan [4] and called the BGM wave in works [5] - [7] . According to review [7] , Wang, Mai, and Niraula [8] and Wei, Liu, and Fang [9] have theoretically obtained the same result but after the Melkumyan discovery. It was also found in book [10] that the BGM wave can exist in certain propagation directions along the free surface of cubic PEM solids. Many cuts can be found in the transversely isotropic (6 mm) PEM materials when the propagation directions satisfy the perpendicularity condition to the sixfold symmetry axis [3] . The surface BGM wave [5] [10] can actually propagate significantly slower than the corresponding piezoelectromagnetic SH-BAW. In this paper, the eighth and tenth new PEM SH-SAWs discovered in papers [11] and [12] , respectively, are studied to record the possible fact that these new waves can propagate (significantly) slower than the BGM wave. These new waves can propagate under the following boundary conditions applied to the suitable free surface of a PEM solid (interface between the solid and a vacuum): mechanically free surface, continuity of both the electrical (φ) and magnetic (ψ) potentials, and the continuity of both the electrical (D3) and magnetic (B3) displacement components that are normal to the surface. The BGM wave can propagate under the following boundary conditions: mechanically free, electrically closed (φ = 0), and magnetically open (ψ = 0) surface of the piezoelectromagnetics. All the SH-waves mentioned above relate to pure waves [13] [14] with the anti-plane polarization.
Piezoelectromagnetics similar to piezoelectrics must be noncentrosymmetric monocrystals or two-phase materials to possess the piezoelectric effect. Besides, magnetoelectroelastics as a class of magnetoelectric materials can have the piezomagnetic and magnetoelectric effects. The smart magnetoelectric materials have mechanical, electrical, and magnetic subsystems and the last two subsystems can affect each other via the first one. This property makes these smart materials multi-promising for various technical applications, for instance, see in review papers [15] - [19] . These smart materials can be also called for development of spintronics representing an electronics free of electric charges. It is obvious that piezoelectromagnetics can be used instead of piezoelectrics in wireless SAW devices. For instance, the development of the SAW sensing technology towards wireless and batteryless can provide cost effective and elegant solutions to the challenges posed by rotating machine components [20] . So, SAW temperature sensors cannot demand either batteries or an external power supply and can offer a lower maintenance and environmentally friendly solution of indoor and outdoor temperature measurements. It is worth here noticing that the utilization of piezoelectromagnetics instead of piezoelectrics is more preferable to experimentally generate anti-plane polarized acoustic waves with the noncontact method [21] - [23] called the electromagnetic acoustic transducers (EMATs).
The following section acquaints the reader with the analytical study of the nondispersive SH-waves. The main purpose is to investigate the eighth [11] and tenth [12] new PEM SH-SAWs in comparison with the other known SH-SAW called the surface BGM wave and the corresponding SH-BAW. These SH-waves are treated as functions of the electromagnetic constant α to record possible peculiarities. For instance there can exist some crossing and extreme points and existence conditions are also of an interest. Therefore, Sections 3, 4, 5, and 6 serve to brace the theoretical research of the following section.
2. Analytical Study
It is natural to first introduce the definition for the speed of the shear-horizontal bulk acoustic wave (SH-BAW), propagation of which is coupled with both the electrical and magnetic potentials. This is useful because the value of the SH-BAW velocity Vtem must be larger than the values of the corresponding SH-SAW velocities, for instance, the surface Bleustein-Gulyaev-Melkumyan (BGM) wave velocity VBGM. The SH-BAW velocity Vtem can then be defined by the following well-known formula:
 (1)
(1)
In Equation (1), 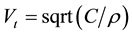 is the purely mechanical SH-BAW velocity. This means that this SH-BAW is uncoupled with both the electrical and magnetic potentials. Also, C, ρ, and
is the purely mechanical SH-BAW velocity. This means that this SH-BAW is uncoupled with both the electrical and magnetic potentials. Also, C, ρ, and  stand for the elastic stiffness constant, mass density, and the coefficient of the magnetoelectromechanical coupling (CMEMC), respectively. The CMEMC being a very important characteristic of a piezoelectromagnetics couples all the material parameters, but the mass density ρ, and reads as follows:
stand for the elastic stiffness constant, mass density, and the coefficient of the magnetoelectromechanical coupling (CMEMC), respectively. The CMEMC being a very important characteristic of a piezoelectromagnetics couples all the material parameters, but the mass density ρ, and reads as follows:
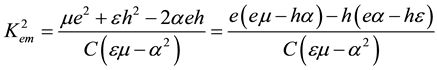 (2)
(2)
In definition (2) one can find the following independent nonzero material constants: the stiffness constant C, piezomagnetic coefficient h, piezoelectric constant e, dielectric permittivity coefficient ε, magnetic permeability coefficient μ, and electromagnetic constant α [5] [10] - [12] .
It is a natural choice to compare the velocity behaviors of the eighth and tenth new SH-SAWs recently discovered in papers [11] and [12] , respectively, with the SH-BAW Vtem and SH-SAW VBGM. This is constructive because there is an assumption that the new SH-waves can propagate even slower than the surface BGM wave in dependence on the electromagnetic constant α. This statement must be demonstrated in the analysis developed below. It is essential to state right away that the SH-SAW VBGM can propagate when the following mechanical, electrical, and magnetic boundary conditions are applied to the interface between the PEM solid and a vacuum: mechanically free surface, electrically closed surface (electrical potential φ = 0) and magnetically open surface (magnetic potential ψ = 0). For the same mechanical boundary condition, the propagation of the eighth and tenth new SH-SAWs [11] [12] requires more complicated electrical and magnetic boundary conditions at the interface: the continuity of both the electrical and magnetic potentials and the continuity of both the normal components of the electrical and magnetic displacements.
So, let’s now introduce the formula for calculation of the BGM wave velocity VBGM that can be derived in the following form:
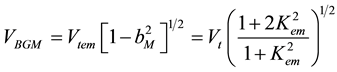 (3)
(3)
where
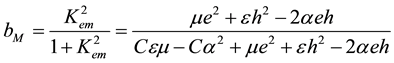 (4)
(4)
The eighth new SH-SAW velocity Vnew8 [11] can be also expressed in the following explicit form:
 (5)
(5)
where
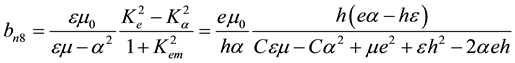 (6)
(6)
It is clearly seen in expressions (5) and (6) that the eighth new SH-SAW cannot exist for the case of zero value of the electromagnetic constant, α = 0, because 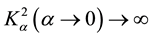 occurs. This is similar to the fifth new PEM SH-SAW discovered in book [5] for the other electrical and magnetic boundary conditions, because its speed is equal to zero as soon as α = 0. It was demonstrated in paper [24] that the value of the fifth new PEM SH-SAW velocity is too close, namely significantly closer than the other new SH-SAW velocities [5] , to the value of the SH-BAW velocity Vtem. Therefore, it is expected that the penetration depth of this new SH-SAW must be significantly larger than that for the other SH-SAWs.
occurs. This is similar to the fifth new PEM SH-SAW discovered in book [5] for the other electrical and magnetic boundary conditions, because its speed is equal to zero as soon as α = 0. It was demonstrated in paper [24] that the value of the fifth new PEM SH-SAW velocity is too close, namely significantly closer than the other new SH-SAW velocities [5] , to the value of the SH-BAW velocity Vtem. Therefore, it is expected that the penetration depth of this new SH-SAW must be significantly larger than that for the other SH-SAWs.
In expression (6), µ0 is the magnetic constant for a vacuum and the following useful equalities were exploited:
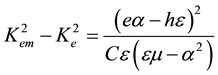 (7)
(7)
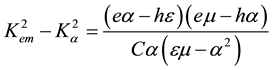 (8)
(8)
In expressions (6) and (7), the coefficient of the electromechanical coupling (CEMC) denoted by 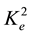 is defined as follows:
is defined as follows:
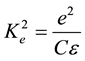 (9)
(9)
The other parameter denoted by 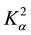 in expressions (6) and (8) couples only the terms with the electromagnetic constant α and equals to the following:
in expressions (6) and (8) couples only the terms with the electromagnetic constant α and equals to the following:
 (10)
(10)
The second new wave for comparison called the tenth new SH-SAW [12] is characterized by the following propagation speed:
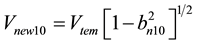 (11)
(11)
where

It is also clearly seen in expressions (11) and (12) that the tenth new SH-SAW cannot exist for α = 0. This is like the eighth new SH-SAW introduced and in some measure discussed above. In expression (12), ε0 is the electric constant for a vacuum and the coefficient of the magnetomechanical coupling (CMMC,

Also, equality (8) and the following equality were used in expression (12):

It is clearly seen in expressions (5) and (6) that the velocity Vnew8 can reach the SH-BAW velocity Vtem as soon as the following condition is completed:

Analyzing expressions (11) and (12), one can also find the following condition for the case of Vnew10 = Vtem:

It is necessary to state that conditions (15) and (16) are also fulfilled when the 



It is apparent that three conditions from (15) to (17) require corresponding large values of the electromagnetic constant α. It is also essential to provide the other conditions relating to the existence of the eighth and tenth new SH-SAWs. It is flagrant in definition (10) that 



Figure 1 shows the dependence of the dimensionless parameters bn8 and bn10 on the normalized value of α2/εµ. The logarithmic scale is used for the later parameter in the figure to soundly demonstrate the peculiarity of the wave existence. The value of εµ is constant in the calculation. This means that only the value of the electromagnetic constant α is changed. The used material parameters of a vacuum are well-known: the magnetic permeability constant is 


a vacuum. These parameters for the composite materials listed in Table 1 are: 



Figure 1. The dimensionless parameters bn8 (black lines) and bn10 (gray lines) versus the normalized value of α2/εµ for the PZT-5H?Terfenol-D (PZT-TD, thick lines) and BaTiO3? CoFe2O4 (BTO-CFO, thinner lines) piezoelectromagnetic composites.
Table 1. The material parameters of the (6 mm) piezoelectromagnetic composites: BaTiO3?CoFe2O4 (BTO-CFO) and PZT- 5H?Terfenol-D (PZT-TD). Here, the values of

BaTiO3?CoFe2O4. It is necessary here to state that the magnetic permeability constant μ for the first composite is only twice as much in comparison with that for a vacuum. It is possible that this fact results in some peculiarities discussed below.
For comparison, the calculations are performed for the following two piezoelectromagnetic composite materials: PZT-5H?Terfenol-D and BaTiO3?CoFe2O4. The material constants of the composites together with the other characteristics are listed in Table 1. The values of the material constants of the studied composites were borrowed from papers [24] [26] - [28] . According to the table, the value of the CMEMC (2) for the PZT-5H? Terfenol-D composite is significantly larger than that for the second material. This fact actually results in the possible existence of the studied new SH-SAWs at small values of the electromagnetic constant α and therefore small normalized values of α2/εµ. The eighth new SH-SAWs cannot exist when the value of α2/εµ is smaller than ~6.4 ´ 10?3 for the PZT-5H?Terfenol-D composite because the parameter bn8 becomes less than ?1, see also Figure 1 and existence condition (18). For BaTiO3?CoFe2O4, the values of α2/εµ must be smaller than ~5.0 ´ 10?7 to get bn8 < ?1. This means that there is the threshold value of α2/εµ to allow the eighth new SH-SAW to exist for either studied composite: α2/εµ ~ 6.4 ´ 10?3 for the PZT-5H?Terfenol-D and α2/εµ ~ 5.0 ´ 10?7 for BaTiO3?CoFe2O4.
For the tenth new SH-SAW existence satisfying condition (19), the threshold values of α2/εµ are significantly smaller, namely α2/εµ ~ 4.8 ´ 10?8 for the PZT-5H?Terfenol-D and α2/εµ ~ 5.0 ´ 10?9 for BaTiO3?CoFe2O4. This means that the propagating waves can exist when the value of α is larger than the threshold value, αth. In fact, a measured value of α is in general very small. This is not undesirable for a piezoelectromagnetic composite material concerning the existence of the eighth and tenth new SH-SAWs because a small proper value of α can cause a significant slowing down of at least one of the new SH-SAW velocities. This is the dramatic influence of the weak magnetoelectric effect on the existence and propagation of the new waves. It is also possible to shortly note that this theoretical report has an interest in a study of propagating (nondissipative) new SH-SAWs characterized by real speeds. Therefore, any dissipation corresponding to the case of α < αth resulting in an imaginary speed is not treated here.
It is also possible to compare with some experimental data for the BaTiO3?CoFe2O4 composite: α2/εµ ~ 4 ´10?5 [29] and α2/εµ ~ 5 ´ 10?6 [30] . The smaller experimental value of α [30] can lead to slower speed of either new wave. It is well-known that composite materials are used because they can demonstrate significantly larger values of the electromagnetic constant α in comparison with magnetoelectric monocrystals. The difference can even reach several orders. However, the Sr3Co2Fe24O41 Z-type hexaferrite [15] with a hexagonal structure was discovered in 2010 that possesses the sufficient magnetoelectric effect for practical applications. For the purpose of slowing down the new wave, the suitable smaller values of α are sensationally more preferable. Therefore, magnetoelectroelastic monocrystals with a weak magnetoelectric effect are welcomed for the purpose of the new wave research. It is necessary to record their material parameter in the literature, including the electromagnetic constant α.
However there is also one peculiarity for the eighth new SH-SAW existence for the PZT-5H?Terfenol-D composite that can be seen in Figure 1 and Figure 2. Indeed, this SH-wave cannot also exist when the value of α2/εµ is larger than ~0.997, assuming that α2/εµ < 1 must occur due to the following limitation: α2 < εµ [18] [19] . It is clearly seen in the figures that this peculiarity can be revealed only for the eighth new SH-SAW in the PZT-5H?Terfenol-D. This also results in a dramatic slowing down of the eighth new SH-SAW. It is thought however that such large values of α do not represent an interest because they are hardly reachable for known composite materials. One can find an extra oddness in Figure 2: the eighth and tenth new SH-SAW speeds can actually be dramatically slower than the speed of the surface Bleustein-Gulyaev-Melkumyan wave for small enough values of α, and VBGM < Vtem should always occur. These facts are more clearly seen in figure 2 for the eighth new SH-SAW (thick solid black line) in the PZT-5H?Terfenol-D. Therefore, it is possible to analytically treat the possible cases of Vnew8 = VBGM and Vnew10 = VBGM similar to the cases of Vnew8 = Vtem and Vnew10 = Vtem considered above.
3. Comparison of Vnew8 and Vnew10 with VBGM
Figure 2 shows the dependence of the velocities Vnew8, Vnew10, VBGM, and Vtem on the electromagnetic constant α (α2/εµ with εµ = const) when the calculations are carried out for both the PZT-5H?Terfenol-D and BaTiO3? CoFe2O4 composites. It is clearly seen in the figure that for the first composite the velocities Vnew8 (thick
Figure 2. The velocities Vnew8 (thick solid lines), Vnew10 (thinner solid lines), VBGM (dashed lines), and Vtem (dotted lines) [all in m/s] versus the normalized value of α2/εµ for the PZT-5H?Terfenol-D (PZT-TD, black lines) and BaTiO3?CoFe2O4 (BTO-CFO, gray lines).
solid black line) and VBGM (dashed black line) can have a crossing point at a small value of the α. For a significantly smaller value of the α, the velocities Vnew10 and VBGM can also have a crossing point. Besides, Figure 2 evidently shows that the velocities Vnew8 and VBGM can have two crossing points for the PZT-5H?Terfenol-D composite: at 

So, let’s first treat the following case:

It is more convenient to treat the following equality instead of equality (20), see formulae (4) and (6):

Employing formulae (4) and (6), equality (21) leads to the following quadratic equation to find unknown values of the electromagnetic constant α:

So, two crossing points must exist in the common case because Equation (22) can have two equation roots. They can be calculated with the following expression:

To have real values of the electromagnetic constant α, it is apparent that the following inequality must be satisfied under the square root in expression (23):

It is obvious that the left-hand part in the inequality can always be larger than zero. The case of ε > 0 results in the fact that the right-hand part must be also larger than zero because the vacuum magnetic constant µ0 > 0. Figure 2 clearly shows that the crossing point occurs at a small value of α2/εµ. Therefore, inequality (24) can be surely written as follows:

Inequality (24) allows one to simplify formula (23). Indeed, formula (23) can be schematically introduced as





Let’s now analyze the existence of the crossing points between the velocities Vnew10 and VBGM. They occur when the following equality is satisfied:

Analogically, it is more convenient to use the following equality instead:

Utilizing formulae (4) and (12), equality (29) can be expanded to the following quadratic equation:

Accordingly, two equation roots can be inscribed as follows:

One has to deal here with the case of real roots of quadratic equation (30). This requires satisfaction of the following inequality:

It is even possible to write the following inequality because equality (28) occurs at a very small value of the electromagnetic constant α:

Using condition (33), equation roots (31) can be rewritten in the following simplified forms:


Comparing the cases of Vnew8 = VBGM and Vnew10 = VBGM, it is possible to conclude that the presence of the vacuum electric constant ε0 results in the smaller value of the electromagnetic constant α, at which there is the crossing point. Two crossing points can actually exist in either case but the second crossing point can be revealed at α2/εµ > 1. Therefore, Figure 2 shows two crossing points only for the case of the eighth new SH-SAW propagating on the surface of the PZT-5H?Terfenol-D composite.
4. The First Derivatives
The analysis carried out above is not complete because one can find several extreme points in the dependence of the eighth new SH-SAW velocity on the normalized value of α2/εµ shown in Figure 2 for the PZT-5H?Terfenol-D composite. Indeed, it is necessary to know the number of the extreme and inflexion points for both the dependences Vnew8(α) and Vnew10(α). It is well-known that there is a closely linear dependence around an inflexion point and this quasi-linear regime can be used in construction of different technical devices. Also, one can find that the Vtem and VBGM velocities can have a smooth minimum in Figure 2. Therefore, it is natural to begin the analysis of the dependencies Vtem(α) and VBGM(α).
The dependence Vtem(α) is given by formula (1) at the beginning of this section. The first derivative of the SH-BAW velocity Vtem [6] [24] with respect to the electromagnetic constant α can be expressed as follows:

where the purely mechanical SH-BAW velocity Vt is defined right away after Equation (1).
This first derivative must be equal to zero at an extreme point. This can happen when the first derivative on the right-hand side is equal to zero. In expression (36), the first derivative of the coefficient of the magnetoelectromechanical coupling 

where the coefficient 
Utilizing expression (8), one can solidly find that there are two extreme points for the dependence Vtem(α). They are given by equalities (15) and (16). Indeed, the dependence 

Concerning the dependence VBGM(α) defined by expressions (3) and (4), its first derivative with respect to the α can be also borrowed from recently published paper [6] . So, one can write down:

Next, it is clearly seen in expression (38) that the dependencies Vtem(α) and VBGM(α) actually have the same extreme points defined by equalities (15) and (16). This is so because this problem reduces to the treatment of Equation (37) for both the cases. However, one can also find an extra possibility given by the expression in the square brackets on the right-hand side of expression (38). Therefore, one must equal to zero the square brackets to check a possible existence of some extra extreme point. After several transformations, one can find that this problem is reduced to the following equality 
It is now possible to find the extreme points for both the dependences Vnew8(α) and Vnew10(α) defined by expressions (5) and (11), respectively. Expressions (6) and (12) depend on the coefficient 

The existence of the extreme points requires that the first derivatives of the velocities Vnew8(α) and Vnew10(α) with respect to the electromagnetic constant α must be equal to zero. Therefore, the following expressions must be considered:


where


First of all, it is necessary to analyze expression (40). Using expressions (6) and (8), it is possible to mark that two terms on the right-hand side of Equation (40) have the same factor such as

This equation can be simplified to the following form:

It is possible to exclude the factor of 

As a result, the final equation representing a polynomial of the eight degree in the unknown parameter α must also have several extreme points. It reads:

where

For the analysis of expression (41), it is essential to use expressions (8) and (12). With expression (8), it is obvious that 



All the extreme points can be revealed by solving the following homogeneous equation:

Proper transformations based on expressions (2), (8), (10), and (12) can lead to the following simplified form:

This form can be further simplified. For instance, the following equality must be employed for expression (12):

Thus, the reader has to cope with the following polynomial of the eighth degree in the unknown parameter α, where the function x(α) is defined by expression (48):

Unfortunately, polynomials (47) and (52) are not simple to analyze and therefore, they can be studied numerically. All the extreme points corresponding to the values of α2/εµ from zero to unity are shown in Figure 2. For the eighth new SH-SAW, the calculated extreme points, see also in Figure 2, can exist at the following values of the normalized parameter α2/εµ: (1) α2/εµ ~ 0.143641 (maximum, Vnew8 ~ 1687.238 m/s), (2) α2/εµ ~ 0.278784 (minimum, Vnew8 ~ 1684.997 m/s), and (3) α2/εµ ~ 0.974169 (maximum, Vnew8 ~ 2019.895 m/s) for PZT-5H? Terfenol-D; and (1) α2/εµ ~ 0.000484 (maximum, Vnew8 ~ 2976.023 m/s) and (2) α2/εµ ~ 0.156816 (minimum, Vnew8 ~ 2952.933 m/s) for BaTiO3?CoFe2O4. It is worth noting that with a thorough analysis of the computation data for PZT-5H?Terfenol-D, the value of α2/εµ ~ 0.278784 corresponding to the minimum of the velocity Vnew8 is the same for the other velocities mention in this theoretical research such as Vnew10, VBGM, and Vtem. It is interesting to compare this value of α2/εµ ~ 0.278784 obtained in the numerical calculation with the value of α2/εµ ~ 0.2793 calculated from equality 


For the tenth new SH-SAW, the calculated extreme points can be also given here below. They correspond to the following values of the normalized parameter α2/εµ: (1) α2/εµ ~ 4.096 ´ 10−5 (maximum, Vnew10 ~ 1773.2165 m/s) and (2) α2/εµ ~ 0.278784 (minimum, Vnew10 ~ 1684.997 m/s) for PZT-5H?Terfenol-D; and (1) α2/εµ ~ 2.401 ´ 10-5 (maximum, Vnew10 ~ 2979.395 m/s) and (2) α2/εµ ~ 0.156816 (minimum, Vnew10 ~ 2952.933 m/s) for BaTiO3?CoFe2O4. It is also possible to write down the values of α2/εµ calculated with conditions 

5. The Second Derivatives
The second derivative can provide information on all possible inflexion points and therefore, reveal a linear regime around an inflexion point that can be useful for experimentalists and theoreticians. It is natural to start the analysis with the partial second derivative of the SH-BAW velocity Vtem with respect to the electromagnetic constant α. It can be also borrowed from work [6] . Thus, all possible inflexion points can be computed by equaling to zero the right-hand side of the following expression:

where

It is convenient to utilize the following definition to calculate the partial second derivative of the velocity VBGM:

where the first and second derivatives of the 
Regarding the partial second derivatives of the new SH-SAWs with respect to the material parameter α, they can be evaluated with the following complicated formulae:


where


The extreme points’ existence requires that the partial second derivatives of the functions Vnew8(α) and Vnew10(α) with respect to the electromagnetic constant α must be equal to zero. All the partial first and second derivatives on the right-hand sides of expressions from (56) to (59) are defined above. Note that expressions from (56) to (59) are as difficult as those obtained for the other new wave velocities studied in papers [6] [24] . Therefore, these complicated dependencies can be studied only by a numerical simulation. This report has no purpose to develop a numerical method to study all the obtained derivatives.
6. The Parameters Δ
The other useful parameter must be also discussed in this paper. This parameter denoted by Δ was first introduced in book [5] and further studied in paper [24] . To treat the parameter Δ is useful because the value of an SH-SAW velocity is frequently situated just below the value of the SH-BAW velocity Vtem. As a result, the difference between the velocities can be as small as several meters per second or even less, or even often mm/s for a weak piezoelectromagnetics. So, Figure 3 compares the following parameters Δ:
Figure 3. The values of established parameters ΔM (dashed lines), Δn8 (thick solid lines), and Δn10 (thinner solid lines) [all in m/s] versus the normalized electromagnetic constant α2/εµ for the PZT-5H?Terfenol-D (PZT-TD, black lines) and BaTiO3?CoFe2O4 (BTO-CFO, gray lines).



It is clearly seen in Figure 3 that all the parameters Δ cannot have a negative sign because an SH-SAW speed must be slower than the SH-BAW speed Vtem. The parameter ΔM never equals to zero because the BGM speed can never reach the SH-BAW speed Vtem, see the dashed lines in Figure 3 for both the composites listed in the table. On the other hand, the other parameters such as Δn8 and Δn10 can be both larger and smaller than the parameter ΔM. Indeed, the value of the parameter Δn8 (thick solid lines) can be significantly larger than the ΔM value at small enough values of the electromagnetic constant α. For significantly smaller values of the α given in the context of Section 2 after existence conditions (18) and (19), this fact must be also true for the other parameter Δn10. Also, it looks like that the Δn8 value can equal to zero for both the studied composites. This means that the speed of the eighth new SN-SAW can reach the SH-BAW speed Vtem. The dependencies Δn10(α) look like they have one smooth minimum for each composite and the tenth new SH-SAW speed cannot touch the bulk wave speed.
So, it is possible to analytically consider the extreme and inflection points of the discussed parameters Δ. For the extreme points’ determination, the following equalities must be treated:



In expressions from (63) to (65), the partial first derivatives on the right-hand sides can be found in the previous sections. To find inflexion points in the dependencies Δ(α), one has to consider the following partial second derivatives with respect to the electromagnetic constant α:



The reader is already familiar with all the partial second derivatives present on the right-hand sides of equalities (66), (67), and (68). These derivatives are quite complicated and can be computed by using the theory developed in the previous section.
7. Conclusion
Exploiting the transversely isotropic (6 mm) magnetoelectroelastic composites such as BaTiO3?CoFe2O4 and PZT-5H?Terfenol-D, it was demonstrated that the magnetoelectric effect can dramatically affect the velocities of the studied nondispersive new SH-SAWs. This is true even in the case of a very small electromagnetic constant α because this small material parameter can result in dramatic slowing down the propagation speeds of the studied new SH-SAWs and even wave propagation loss. Also, analytical investigations of the studied new SH-SAW velocities were performed: the extreme and inflexion points were evaluated and discussed. The illuminated peculiarities can be useful for technical device construction based on the magnetoelectric effect and the effect of the slow speed can also find some practical applications, for instance, in filters such as delay lines, etc. The found peculiarities can be also involved in the study on better understanding of the magnetoelectric effect.
Cite this paper
Aleksey AnatolievichZakharenko, (2015) Dramatic Influence of the Magnetoelectric Effect on the Existence of the New SH-SAWs Propagating in Magnetoelectroelastic Composites. Open Journal of Acoustics,05,73-87. doi: 10.4236/oja.2015.53007
References
- 1. Bleustein, J.L. (1968) A New Surface Wave in Piezoelectric Materials. Applied Physics Letters, 13, 412-413.
http://dx.doi.org/10.1063/1.1652495 - 2. Gulyaev, Yu.V. (1969) Electroacoustic Surface Waves in Solids. Soviet Physics Journal of Experimental and Theoretical Physics Letters, 9, 37-38.
- 3. Gulyaev, Yu.V. (1998) Review of Shear Surface Acoustic Waves in Solids. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 45, 935-938.
http://dx.doi.org/10.1109/58.710563 - 4. Melkumyan, A. (2007) Twelve Shear Surface Waves Guided by Clamped/Free Boundaries in Magneto-Electro-Elastic Materials. International Journal of Solids and Structures, 44, 3594-3599.
http://dx.doi.org/10.1016/j.ijsolstr.2006.09.016 - 5. Zakharenko, A.A. (2010) Propagation of Seven New SH-SAWs in Piezoelectromagnetics of Class 6 mm. LAP LAMBERT Academic Publishing GmbH & Co. KG, Saarbruecken-Krasnoyarsk, 84 p.
- 6. Zakharenko, A.A. (2011) Analytical Investigation of Surface Wave Characteristics of Piezoelectromagnetics of Class 6 mm. International Scholarly Research Network (ISRN) Applied Mathematics, 2011, Article ID: 408529.
http://dx.doi.org/10.5402/2011/408529 - 7. Zakharenko, A.A. (2013) Piezoelectromagnetic SH-SAWs: A Review. Canadian Journal of Pure & Applied Sciences (SENRA Academic Publishers, Burnaby, British Columbia, Canada), 7, 2227-2240.
- 8. Wang, B.L., Mai, Y.-W. and Niraula, O.P. (2007) A Horizontal Shear Surface Wave in Magnetoelectroelastic Materials. Philosophical Magazine Letters, 87, 53-58.
http://dx.doi.org/10.1080/09500830601096908 - 9. Wei, W.-Y., Liu, J.-X. and Fang, D.-N. (2009) Existence of Shear Horizontal Surface Waves in a Magneto-Electro-Elastic Material. Chinese Physics Letters, 26, Article ID: 104301.
- 10. Zakharenko, A.A. (2011) Seven New SH-SAWs in Cubic Piezoelectromagnetics. LAP LAMBERT Academic Publishing GmbH & Co. KG, Saarbruecken-Krasnoyarsk, 172 p.
- 11. Zakharenko, A.A. (2013) New Nondispersive SH-SAWs Guided by the Surface of Piezoelectromagnetics. Canadian Journal of Pure & Applied Sciences, 7, 2557-2570.
- 12. Zakharenko, A.A. (2015) A Study of New Nondispersive SH-SAWs in Magnetoelectroelastic Medium of Symmetry Class 6 mm. Open Journal of Acoustics, 5. (in press)
- 13. Lardat, C., Maerfeld, C. and Tournois, P. (1971) Theory and Performance of Acoustical Dispersive Surface Wave Delay Lines. Proceedings of the IEEE, 59, 355-364.
http://dx.doi.org/10.1109/PROC.1971.8177 - 14. Dieulesaint, E. and Royer, D. (1980) Elastic Waves in Solids: Applications to Signal Processing. Wiley, New York, Chichester [English], Translated by Bastin, A. and Motz, M., 511 p.
- 15. Kimura, T. (2012) Magnetoelectric Hexaferrites. Annual Review of Condensed Matter Physics, 3, 93-110.
http://dx.doi.org/10.1146/annurev-conmatphys-020911-125101 - 16. Pullar, R.C. (2012) Hexagonal Ferrites: A Review of the Synthesis, Properties and Applications of Hexaferrite Ceramics. Progress in Materials Science, 57, 1191-1334.
http://dx.doi.org/10.1016/j.pmatsci.2012.04.001 - 17. Srinivasan, G. (2010) Magnetoelectric Composites. Annual Review of Materials Research, 40, 153-178.
http://dx.doi.org/10.1146/annurev-matsci-070909-104459 - 18. Özgür, ü., Alivov, Ya. and Morkoç, H. (2009) Microwave Ferrites, Part 2: Passive Components and Electrical Tuning. Journal of Materials Science: Materials in Electronics, 20, 911-952.
http://dx.doi.org/10.1007/s10854-009-9924-1 - 19. Fiebig, M. (2005) Revival of the Magnetoelectric Effect. Journal of Physics D: Applied Physics, 38, R123-R152.
http://dx.doi.org/10.1088/0022-3727/38/8/R01 - 20. Durdag, K. (2009) Wireless Surface Acoustic Wave Sensors. Sensors and Transducers Journal, 106, 1-5.
- 21. Thompson, R.B. (1990) Physical Principles of Measurements with EMAT Transducers. In: Mason, W.P. and Thurston, R.N., Eds., Physical Acoustics, Academic Press, New York, Vol. 19, 157-200.
http://dx.doi.org/10.1016/b978-0-12-477919-8.50010-8 - 22. Hirao, M. and Ogi, H. (2003) EMATs for Science and Industry: Non-Contacting Ultrasonic Measurements. Kluwer Academic, Boston.
http://dx.doi.org/10.1007/978-1-4757-3743-1 - 23. Ribichini, R., Cegla, F., Nagy, P.B. and Cawley, P. (2010) Quantitative Modeling of the Transduction of Electromagnetic Acoustic Transducers Operating on Ferromagnetic Media. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 57, 2808-2817.
http://dx.doi.org/10.1109/TUFFC.2010.1754 - 24. Zakharenko, A.A. (2012) On Wave Characteristics of Piezoelectromagnetics. Pramana—Journal of Physics, 79, 275-285.
http://dx.doi.org/10.1007/s12043-012-0308-3 - 25. Zakharenko, A.A. (2015) On Separation of Exchange Term from the Coefficient of the Magnetoelectromechanical Coupling. Pramana—Journal of Physics, 85. (In press)
- 26. Wang, B.-L. and Mai, Y.-W. (2007) Applicability of the Crack-Face Electromagnetic Boundary Conditions for Fracture of Magnetoelectroelastic Materials. International Journal of Solids and Structures, 44, 387-398.
http://dx.doi.org/10.1016/j.ijsolstr.2006.04.028 - 27. Liu, T.J.-Ch. and Chue, Ch.-H. (2006) On the Singularities in a Bimaterial Magneto-Electro-Elastic Composite Wedge under Antiplane Deformation. Composite Structures, 72, 254-265.
http://dx.doi.org/10.1016/j.compstruct.2004.11.009 - 28. Zakharenko, A.A. (2014) Investigation of SH-Wave Fundamental Modes in Piezoelectromagnetic Plate: Electrically Closed and Magnetically Closed Boundary Conditions. Open Journal of Acoustics, 4, 90-97.
http://dx.doi.org/10.4236/oja.2014.42009 - 29. Aboudi, J. (2001) Micromechanical Analysis of Fully Coupled Electro-Magneto-Thermo-Elastic Multiphase Composites. Smart Materials and Structures, 10, 867-877.
http://dx.doi.org/10.1088/0964-1726/10/5/303 - 30. Wang, Y.-Z., Li, F.-M., Huang, W.-H., Jiang, X., Wang, Y.-Sh. and Kishimoto, K. (2008) Wave Band Gaps in Two-Dimensional Piezoelectric/Piezomagnetic Phononic Crystals. International Journal of Solids and Structures, 45, 4203-4210.
http://dx.doi.org/10.1016/j.ijsolstr.2008.03.001





