Open Journal of Acoustics
Vol.05 No.01(2015), Article ID:54522,13 pages
10.4236/oja.2015.51002
Ultrasound Imaging in Nuclear Reactors Cooled by Liquid Metals
Victor D. Svet, Dmitrii A. Dement'ev
OJSC “N. N. Andreyev Acoustical Institute”, Moscow, Russia
Email: vsvetd@mail.ru
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 February 2015; accepted 6 March 2015; published 10 March 2015
ABSTRACT
In nuclear reactors cooled by liquid metals, ultrasound is the only type of field that allows obtaining images of the reactor cores and diagnostics of the integrity of the fuel assemblies. The article discusses the features of the practical realization of ultrasonic imaging systems based on phased arrays and offers an alternative solution of imaging on the basis of the acoustic lenses of refractive and diffraction types. Using lenses eliminates many of the technical and technological problems associated with the development of multi-element phased arrays. It is shown that lens systems allow using traditional methods of transformation of acoustic fields into the visible images by 2D piezo matrix and a more promising way of acoustooptical transformation based on coherent optical interferometry.
Keywords:
Ultrasound Imaging, Phased Arrays, Liquid Metals, Nuclear Reactors, Acoustic Lens

1. Introduction
Ultrasound imaging (UI) of objects located in molten metals is one of the most pressing problems of nondestructive testing in various industrial areas. Especially it is required in nuclear reactors cooled by liquid lead or sodium, as ultrasound is the only type of field to obtain images of objects disposed in the working zone of the reactor with a required high resolution. Researches in this area are carried out in different countries for decades [1] - [3] , but to our knowledge, there is no commercial ultrasound imaging high-speed system capable to operate at temperatures up to 600˚C and high levels of radiation up to 30 kGy/h. The developed systems of ultrasonic imaging are based on the use of several transducers with their mechanical scanning in different planes. Such systems have low imaging speed and the mechanical scanning systems are quite complex [4] - [6] . In the overwhelming numbers of publications, multi-element phased arrays (MPA) are considering as the basis of UI [5] - [17] ; so let’s consider the main problems which arise when developing phased arrays for ultrasound imaging in molten metals.
2. Ultrasound Imaging on the Base of Phased Arrays
Phased array is a distributed antenna system consisting of N individual receiving ultrasonic elements (piezoelectric transducers) arranged in a line (linear MPA) or in a two-dimensional matrix of N*N elements. “Mill’s Cross” configuration is often using, where one of the linear arrays is a receiver, and the second orthogonal linear array is a transmitter. Mill’s cross arrays are widely used in ocean acoustic bathymetry, because instead of N2 elements we can use only 2 N elements. It is well known that for high quality imaging receiving elements of array should have dimensions ≤λ/2, where λ―is a wavelength, and they should be regular. These are so called “full sampling arrays”. Having this array it is possible to achieve the maximum viewing sector zone and minimum side field of array. In some applications the value of viewing sector can be reduced and array elements can have dimensions more that wave-length. But in this case the level of side field should be small to avoid unwanted artifacts in the ultrasonic images. The objects of interest in nuclear reactors are fuel rods and fuel assemblies. Their design and location determines the frequency band of ultrasound and hence the entire configuration of a further ultrasound imaging system. A typical image of the fuel element is shown in Figure 1.
The outer diameter of the fuel element is about 9 mm; the total length of fuel element with fastening elements is about 3840 mm. The fuel rods are usually collected in special cassettes (assemblies), a fragment of which is shown in Figure 2. Based on the above dimensions and requirements of NDT it is desirable to have a spatial resolution at least of 0.5 - 1 mm and less.
The most preferable mode is 3D ultrasound imaging. So the values of ultrasonic frequencies should be in the range 2∙∙∙5 MHz. At sound velocity in the molten lead Cl ≈ 1750 m/s, this corresponds to the wavelengths λmax = 0.9 mm, λmin = 0.35 mm. Therefore half-wave dimensions of elements should be from 0.45 mm to 0.18 mm and exactly these small dimensions create serious problems of design of phased arrays for ultrasound imaging in the liquid metals, although, for example, in the ultrasound systems for medicine or NDT such problems do not exist at all. Let’s consider these problems in more detail.
2.1. Small Dimensions of Elements
Piezoelectric element with small dimensions has low capacity, <1 pF. Each element should be connected to a coaxial cable with length more than 15 meters. This is an average distance to signal processing system. Coaxial cables have specific capacity about 100 pF/m or more. This means that the level of the received signal will be reduced in thousands times, and it is necessary to take into account that nuclear power plants have very high levels of electromagnetic interference.
2.2. Low Sensitivity of Piezoelectric Ceramics
Despite the fact that the high-temperature piezoelectric ceramics exists, its sensitivity, defined by piezoelectric modulus d33 or d31 in several times less than that for low-temperature piezoelectric ceramics.
Figure 1. Fuel rod.
Figure 2. Fragment of fuel assembly.
2.3. Homogeneity of Array Elements
High-quality ultrasound imaging with phased arrays requires minimum level of the amplitude-phase spreading in the individual elements. Typical requirements are the following: sensitivity spread should be no more than ±3 dB, and phase spreads should not exceed ±5˚ at a higher frequency. For these requirements the array’s directivity is close to calculated value.
2.4. Acoustical Cross-Talks
The gap between half wave elements in array for specified frequencies should be about 50 - 100 micrometers. In order to eliminate mutual influence of elements the gaps are filled with a special compound, the acoustic impedance of which should be in several times less than acoustic impedance of the piezoelectric element. For low temperatures such compounds are well known. For specified conditions only high-temperature compounds such as epoxy resins can be used and their acoustic impedance is close to the impedance of elements and required decoupling of elements is problematic. According to some published data level of decoupling is (−10 - 12 dB), which is clearly not enough [8] - [10] .
2.5. Temporary Temperature Instability
At high temperatures, the various parameters of PZT are very sensitive to temperature fluctuations (especially value of piezomodules, resonance frequency, etc.) which lead to strong amplitude and phase fluctuations in the received signals.
2.6. Wettability.
Most of the liquid metals have poor wettability, which decrease acoustic contact of array’s elements with the working environment. In particular, lead has poorer wettability. In order to improve the wettability many authors proposed coating of array’s elements with different metal films-gold, nickel and other [9] [10] .
In connection with these problems “half-hearted” solutions are suggested in many publications. First of all, the dimensions of elements in arrays are chosen much larger than the half wavelength [10] [12] . This reduces the value of viewing sector which is determined as
 (1)
(1)
where λ―wavelength of the ultrasound, and d―the dimension of the element. According [14] the dimension of one element in matrix array on 36*36 elements at a frequency 5 MHz, had a size of 2.5 × 2.5 mm, and furthermore, elements were located within 5 mm gap from each other. Array was designed for operation at 200˚C. Therefore view angle of this array should not exceed ±10˚, and moreover because of not full sampling 100% side lobes must appear in array directivity patterns. To provide wide view sector such matrix array had to be mechanically rotated, that virtually “negates” all the advantages of phased arrays. Realizing that a large number of elements in the matrix array create serious technological problems, many authors have “returned” to the development of so- called “randomized” arrays, i.e. arrays with a random arrangement of receiving elements [18] . This old idea, borrowed from radar of 1960th years has well recommended itself in applications for focused ultrasound surgery where it is necessary to create one focal point. However, in our opinion, randomization of arrays is a not good solution because of unpredictable occurrence of additional peaks in directivity patterns and unpredictable level of the side field. Mill’s cross arrays [19] [20] , can provide imaging in a wider viewing sector but they require consistent changing of the vertical beam angle of the transmitting array. Using simultaneous transmission of orthogonal signals in several vertical directions , reduces the output signal/noise ratio, since for any radiated signal at a predetermined vertical angle, all other transmitted orthogonal signals are noise, and, in addition, such a system is quite complex.
This brief review shows that for high quality ultrasound imaging, especially in 3D mode, the dimensions of the receiving elements must be no more half-wavelength and wavelength. And assuming that the connection technology (splicing) of small size elements with coaxial cables is worked out, the compensation of signal losses must be done by preamplifiers in array housing. This design will inevitably require forced cooling.
3. Ultrasonic Lens Imaging
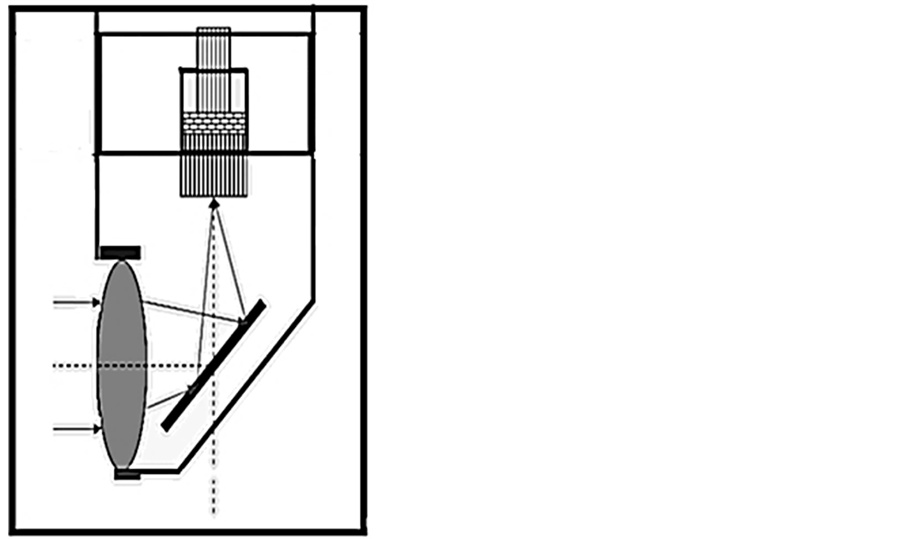
Many of discussed problems can be eliminated if we will use acoustic lenses for imaging instead of phased arrays. Such lens systems are widely used in underwater acoustic imaging and sonar [21] - [23] . The main advantage of this solution is that the acoustic lens automatically forms image in some plane and it can be simply registered. In continuous mode acoustic image is constructed only in the transverse coordinates, and the problem of phasing of individual array elements is automatically eliminated, as only the intensity of image can be registered. Moreover, acoustic lens allows offering a variety of ways of transforming acoustic image into a visible image, which will be discussed later. The disadvantage of lens systems is a rather small view angle. For a single lens, its value is no more than 26˚ - 30˚, but may be extended up to 45˚ - 50˚ by using more complex acoustic lens objective. For operation in the liquid lead or liquid sodium the acoustic lens may be made from metal (steel, titanium, tungsten). Wave size of lens should conform to the required angular resolution at a given frequency. Figure 3 shows the possible arrangements of lens imaging systems. The acoustic lens can be formed as the refractive focusing elements or diffractive lenses.
Figure 3. Variants of arrangements of acoustic lens.
3.1. Refractive Acoustic Lenses
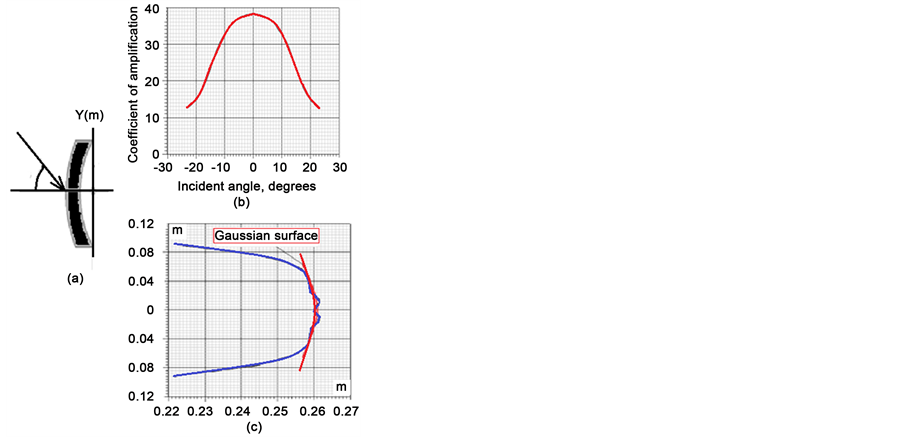
Refractive acoustic lens are similar to a conventional optical lens; the only difference is that depending on the sound speed in the material of the lens and in the environment, the forms of lens can be converging and diverging. The quality of the acoustic image is largely dependent on the parameters of the acoustic lens and its form. It was found that the optimal form of a single lens is convex-concave lens, which has sufficient view angle and a relatively low level of side lobes (without apodization), [23] , Figure 4.
Calculations and experiments have shown that this single simple lens capable to build undistorted image with the given parameters and angular resolution in view sector no more than ±15˚. In the sector of angles ±22.5˚ due to aberrations angular resolution worsens in 1.5 times. So at a frequency of 3.5 MHz in the view sector ±12.5˚ transverse resolution is 0.8 mm, and for view sector ±22.5˚ it increases to 1.3 mm. Figures 5(a)-(c) show a longitudinal section of the acoustic field for angles −20˚, 0˚, 20˚ (Figure 5(a)) and forms of the focal spots at normal incidence (Figure 5(b)) and at an angle of −10˚ (Figure 5(c)).
Figure 4. Calculated parameters of acoustical lens from steel for frequency F = 3.5 MHz and diameter 120 mm. (a) Form of lens; (b) Coefficient of amplification; (c) The form of focal surface in longitudinal section.


Figure 5. Images of longitudinal sections (a); and focal spots (b).
Figure 6(a) shows images of longitudinal sections of 10 of point sources, and. their amplitude distribution in a lateral section (Figure 6(b)).
Photos of acoustic lens made from steel with a diameter of 90 mm and 120 mm for frequencies 3.5 and 1.5 MHz accordingly are presented on Figure 7.
3.2. Diffraction Acoustic Lenses
In acoustics diffraction lenses are known as the “zone plates” or Fresnel lenses. The rapid development of digital optics stimulated again big interest to diffraction lens due to possibility to eliminate the associated diffraction beams and significantly increasing the diffraction efficiency. The basic idea of such a binary structure is that the phase of the diffracted beam may be encoded by different heights of zone rings. In this case, the diffraction efficiency of a coded zone plate is
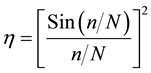 (2)
(2)
where N-number of equal levels of phase encoding. For example, eight coding levels provide 95% diffraction-
Figure 6. Images of focused 10 points in longitudinal (a) and lateral (b) sections.
Figure 7. Prototypes of steel acoustical lenses for frequencies F = 3.5 MHz (left image) and F = 1.5 MHz (right image).
efficiency of zone lens, while conventional refractive lenses have diffraction efficiency of at least 75%. For each level of the coding phase the local ring radius is calculated by the formula
 (3)
(3)
where z0―focal length, λ―wavelength, and the sampling interval is defined as
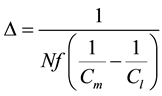 (4)
(4)
where f―frequency, Cm, Cl―sound velocities in the environment and the material of the lens, respectively. Scheme of the diffraction zone lens with 4 coding levels is presented in Figure 8.
Note that for ultrasound imaging in lead binary diffraction lens is of great interest. First of all, its weight is significantly less than weight of refractive lens, and it is much easier for manufacturing. Given the high level of radiation a working zone, lens can be manufactured from a wide range of materials which do not have an increased resistance to radiation, and a lens can be replaced quickly. Moreover, the zone lens has small parasitic reflections from their surfaces in comparison with refractive lens. The only drawback is that diffraction lens has rather narrow frequency band, i.e. such focusing systems have elevated “chromatic” aberration, but this question requires special consideration.
4. Registration of the Signals in the Lens System by PZT Matrix
Let us now consider how to register acoustic image. One of the solutions is based on the use of two-dimensional PZT matrix made of low-temperature ceramics with a big value of the piezoelectric modulus d33. Acoustic coupling of matrix with the liquid metal can be carried out through matrix solid waveguides with a diameter smaller than the ultrasonic wavelength [24] . PZT matrix itself can be located in a small hermetic cooling case, Figure 9(a). Outer ends of the acoustic waveguides can be positioned on a curved surface (Gaussian plane) to minimize the aberration of the lens. The form of this shape is calculated in advance. Decoupling of acoustic waveguides is achieved by their placement in a porous high-temperature ceramics, which acoustic impedance is
Figure 8. Zone binary lens with 4 encoding levels.


Figure 9. (a) Lens imaging system with 2D PZT matrix; (b) Wiring of PZT elements.
much smaller than acoustic impedance of the acoustic waveguide. Porous carbon structures and high temperature silicon resins are also promising materials. The use of different lengths of the acoustic waveguide which output ends are connected with PZT elements allows diluting the connecting wires in space, Figure 9(b). Note also that adding a second lens we can increase the size of the output acoustical image, and increase the dimensions of PZT elements i.e. increase their capacity and weaken the requirements to the next electronics.
Sensitivity of reading system depends on the length of acoustic waveguides and the parameters of the materials from which they are made. If the diameter of the waveguide is less than wavelength the equation for propagation of longitudinal waves is

Boundary conditions are as follows. In the section at X = 0, where the external pressure is applied there is a tension generated by this pressure P:

The second end of the rod at X = l is free and therefore the tension is zero:

The solution of equation with these boundary conditions is given by [24] :

where E and k are related by
For a rod with small damping when

Figure 10 shows the calculated values according to the displacement end of the rod depending on its length at different frequencies at the following initial parameters: the medium-liquid lead, a density of 10.9 ´ 103 kg/m3, the velocity―1750 m/sec. Waveguide has the length l with diameter d, made from steel with a density ρ2 = 2320 kg/m3 and the sound speed C2 = 5500 m/s. The amplitude of the pressure in lead is P = 1 Pa. The amplitude of the pressure in the rod is equal to P = 0.8 Pa.
Note that ultrasonic imaging lens system allows the use of pulse mode for 3D imaging. However, as waveguides have different lengths it is necessary to compensate small time delays, which can be implemented in signal processing unit.
5. Acoustooptical Registration of Image
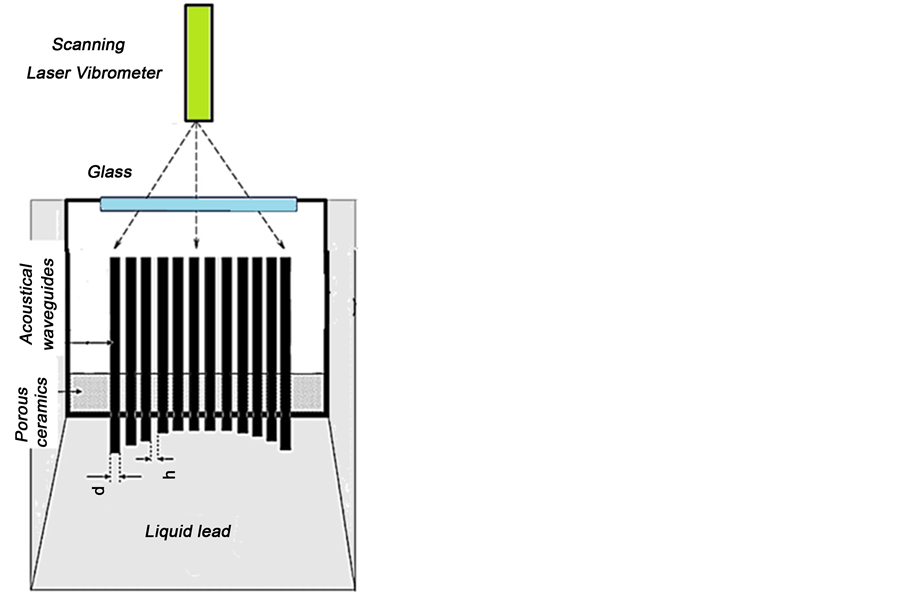
The use of acoustic waveguides allows offering an alternative conversion of acoustical image into visible image by direct acoustooptical transformation, for example by laser vibrometer, Figure 11.
The principle of the laser vibrometer is based on measuring the Doppler frequency shift of light reflected from a moving object. For such measurements optical heterodyne method is commonly used on the basis of a two-beam interferometric optical scheme with the subsequent formation of the quadrature components of the electrical signal and photo detectors of the balanced type. Modern methods of laser vibrometry have a very high sensitivity and resolution in the frequency range of vibrations up to hundreds of MHz’s. For example, a laser vibrometer PSV-500M POLYTEC allows scanning vibrating surface from distances 0.1 m up to 100 meters in the field of view of 50˚*40˚ with angular resolution 0.002˚. Minimum detectable displacement is 10−12 m. The scanning speed is several hundred points/sec. Such high angular resolution allows setting the laser vibrometer at height, for example, 10 meters from the vibrating ends of the waveguides and scanning area will be only 0.35 mm2.
Figure 10. Calculated values of displacements (m) versus length of waveguide (m) for different frequencies. Red―3.6 MHz, Green― 3 MHz, Blue―2.5 MHz.
Figure 11. Reading of acoustical image by laser vibrometer.
It is possible to use other scheme of optical reading, also based on the interferometric optical system, but without a scanning laser [25] . The idea of this scheme is as follows. At a distance d from the output ends of waveguides the plane-convex lens is placing. Plane flat surface of this lens and the plane of the output end form a multichannel Fabry-Perot interferometer. Using a laser and a collimator formed by a plane-convex lens and other lens parallel light beam is forming which illuminates the ends of the waveguides. The reflecting light from the ends is forming an interferometry pattern, which intensity I(x, t) is modulated by the incident acoustic field P(x, t). Modulated distribution I(x, t), via the lens system is projected on the photo-detector matrix, like CCD camera and then enters a signal processing device, where optical image is forming. The distance d between the output ends of the acoustic waveguide and plane-convex lens is as follows:
where ξ―vibrational displacement of the output end of the acoustic waveguide, ωac―circular frequency of the ultrasound, and the gap d0 is chosen from the condition of quadrature detection:

where n―integer and λ―wavelength of light.
The output light intensity of such an interferometer is

where I1 and I2―the intensity of the light waves reflected from the ends of the waveguides and the flat surface of the lens,

Thus the output light intensity is equal to

And when 

i.e., the output optical signal is proportional to the amplitude of the oscillatory displacement (or sound pressure) of the local acoustic waveguide at the working point
Figure 13 shows a possible scheme implementing the method discussed above.
Figure 12. Selection of working point.
Figure 13. Optical reading scheme on the base of interferometer Fabry-Perot. 1. Acoustical lens with transducer; 2. Porous ceramics; 3. Waveguides; 4. Plane-concave lens; 5. Housing; 6, 7. Optical mirrors; 8, 10. Spherical lens; 9. Semiconductor laser; 11. CCD matrix; 12. USB cable; 13. Signal processing unit; 14. Display; 15. Signal generator.
System elements (4-11) are arranged in the housing, from which air is evacuated in order to avoid parasitic effects of refraction of the optical waves in a high temperature environment. The distance d between the output ends of the waveguides and the planar surface of lens diameters and output ends of the waveguides is chosen so that the diffraction divergence of the light from each end of the waveguide is small and reflected light from the output ends do not overlap that minimizes interference of the reflected optical signals. In the presence of field ξ(x, t) spatial distribution of the interference pattern arises and the spatial distribution of the light intensity I(x, t)is proportional to ξ(x, t) ~ P(x, t). Using optical mirrors (6, 7) and the objective (10) the spatial distribution I(x, t) is projected onto the CCD matrix (11), connected with the signal processing device (13). Projecting an image is performed by a double Fourier transformation implemented by a plane-convex lens (4) and the lens (10), having equal focal lengths.
Non-contact optical method for reading the acoustic image has many advantages compared with traditional methods of piezoelectric conversion. First of all, there is no piezoelectric matrix itself and, consequently, all problems related to cooling, distributing large number cables and connections are eliminated. Moreover, high- energy power systems are characterized by high electrical and electromagnetic interference and optical reading is not sensitive to this noise.
6. The Acoustic Transmitter
Source level of ultrasonic transmitter must be sufficiently high. Other important requirement is the uniformity of illumination of the working area. Fortunately, at higher frequencies, generation high levels of acoustic pressure do not constitute a serious problem. For a lens system (no matter of what type), it is conveniently to place transducer n the center of lens because it is practically not “working” for imaging. Another variant is to place transducers around the lens. Below several variants of transmitters and their calculated distribution of the pressure field are presented. Since the frequencies are in the range from 1.5 to 3.5 MHz, the increasing diameter of the radiator to several wavelengths increases its directivity (1). If the dimension of transmitter is about 1 mm or slightly more for the frequency F = 3.5 MHz, it will have the desired directivity about 45˚, but the intensity of radiation will be extremely low, since nigh voltages will destroy such small element. It follows that the transmitter must consist of groups of PZT elements of suitable dimensions. There are several variants of this design. One of the simulated versions is shown in Figure 14(a).
It is a hemisphere covered by elementary transducers or solid hemisphere with a predetermined diameter and radius of curvature. The second embodiment of the transducer is shown in Figure 14(b), and it represents a group of radiating elements disposed along the perimeter of the lens. The signals of all elementary transducers in both versions are transmitting in phase. Below there are some examples of calculated acoustics fields. The first transducer had a diameter 6 cm and a radius of curvature of 10 cm, maximum intensity on the element is approximately 2 W/cm2. We see that from a distance 30 cm, the radiated field has good uniformity and a sufficient view angle. Blue color on Figure 15(a) corresponds to acoustical pressure more than 105 Pa on F = 3 MHz. Figure 15(b) shows the distribution of pressure for the ring transducer consisting of 20 elements with a diameter of 1 cm. This transducer has the same acoustic pressure of 105 Pa with the field in homogeneity about ±3 dB.
7. Conclusion
The discussed peculiarities of ultrasonic imaging in molten metals permit to conclude that lens imaging system
Figure 14. Variants of combined acoustical transmitters (a) in the center of lens (b) ring set of transducers.
Figure 15. Beam patterns of transducers (Figure 14(a) and Figure 14(b)).
compared with phased arrays has many serious advantages and can eliminate many technological and design problems associated with the development of multi-element phased arrays. Lens systems allow realizing as traditional methods of reading signals by 2D PZT matrix and optical interferential methods of transformation of acoustical image into optical one. This variant in our opinion is the most promising technical solution for the development of ultrasonic imaging systems for nuclear reactors’ cooling by liquid metals.
Acknowledgements
The authors thank S. Baykov, L. Gavrilov and S. Petrosyan for help in performing the simulations and K. Mikheev for valuable advices and consultations. The authors are also grateful to the participants of seminar of Prof. S. A. Ribak “Acoustics of inhomogeneous media” for a fruitful discussion of this work.
This work is supported by GRANT RFBR 14-02-00331.
References
- Barrett, L.M., McKnight, J.A. and Forthergill, J.R. (1984) Ultrasonic Viewing in Fast Reactors. Physics in Technology, 15, 308-314. http://dx.doi.org/10.1088/0305-4624/15/6/I03
- Griffin, J.W., et al. (2009) Under Sodium Viewing: A Review of Ultrasonic Imaging Technology for Liquid Metal Fast Reactors. Pacific Northwest National Laboratory, Richland, PNNL-18292.
- Jasiūnienė, E. (2007) Ultrasonic Imaging Techniques for Non-Destructive Testing of Nuclear Reactors, Cooled by Liquid Metals, Review. Ultragarsas (Ultrasound), 62.
- Takagi, K., Otaka, M., Arai, T., Yoda, S., Nagai, S., Suzuki, T., Miura, T. and Karasawa, H. (2000) Development of Novel Visualization Technique of Flow Field for Liquid Metals Using High Temperature Ultrasonic Transducer. Proceedings of the 2000 ASME Fluids Engineering Division Summer Meeting, Boston, 11-15 June 2000, 331-336.
- Kazys, R., Voleisis, A., Sliteris, R., Mazeika, L., Van Nieuwenhove, R., Kupschus, P. and Abderrahim, H.A. (2002) Investigation of Ultrasonic Properties of a Liquid Metal Used as a Coolant in Accelerator Driven Reactors. 2002 IEEE Ultrasonics Symposium, 1, 815-818.
- Bond, L.J., Doctor, S.R., Bunch, K.J., Good, M.S. and Waltar, A.E. (2007) Instrumentation, Monitoring and NDE for New Fast Reactors. Advanced Nuclear Fuel Cycles and Systems (GLOBAL 2007), Boise, 1274-1279.
- Griffin, J.W., Bond, L.J., Jones, A.M. and Peters, T.J. (2010) Design of High Temperature Ultrasonic Linear Arrays for Under-Sodium Viewing. 7th International Topical Meeting on Nuclear Plant Instrumentation, Control and Human Machine Interface Technologies (NPIC&HMIT 2010), Las Vegas, 7-11 November 2010, 1600-1614.
- Abderrahim, H.A., et al. (2003) MYRRHA, a Multi-Purpose Accelerator Driven System for R&D. State-of-the-Art of the Project at Mid-2003. Proceedings of International Workshop on P&T and ADS Development, Mol, Belgium, 6-8 October 2003.
- Kažys, R., Voleišis, A., Šliteris, R., Voleišienė, B., Mažeika, L., Kupschus, P. and Abderrahim, H.A. (2006) Development of Ultrasonic Sensors for Operation in a Heavy Liquid Metal. IEEE Sensors Journal, 6, 1134-1143. http://dx.doi.org/10.1109/JSEN.2006.877997
- Kažys, R., Voleišis, A., Šliteris, R., Mažeika, L., Van Nieuwenhove, R., Kupschus, P. and Abderrahim, H.A. (2005) High Temperature Ultrasonic Transducers for Imaging and Measurements in a Liquid Pb/Bi Eutectic Alloy. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 52, 525-537. http://dx.doi.org/10.1109/TUFFC.2005.1428033
- Kažys, R., Mažeika, L., Jasiūnienė, E., Šliteris, R., Kupschus, P., Van Nieuwenhove, R. and Abderrahim, H.A. (2003) Ultrasonic Imaging Techniques for the Visualization in Hot Metals. Proceedings of the World Congress on Ultrasonics, Paris, 7-10 September 2003, 1391-1394.
- Kažys, R., Mažeika, L., Voleišis, A., Šliteris, R., Jasiūnienė, E., Abderrahim, H.A. and Dierckx, M. (2007) Ultrasonic Imaging in the Liquid Metals. International Journal of Applied Electromagnetics and Mechanics, 25, 249-256.
- Rajendran, A., Asokane, C., Elumalai, G. and Swaminathan, K. (1996) Development of an Ultrasonic Under-Sodium Scanner for the Fast Breeder Test Reactor. Proceedings of the 14th World Conference on Non-Destructive Testing, New Delhi, 8-13 December 1996, 349-352.
- Karasawa, H., Izumi, M., Suzuki, T., Nagai, S., Tamura, M. and Fujimori, S. (2000) Development of Under-Sodium Three-Dimensional Visual Inspection Technique Using Matrix Arrayed Ultrasonic Transducer. Journal of Nuclear Science and Technology, 37, 769-779. http://dx.doi.org/10.1080/18811248.2000.9714955
- Swaminathan, K., Rajendran, A. and Elumalai, G. (1990) The Development and Deployment of an Ultrasonic Under-Sodium Viewing System in the Fast Breeder Test Reactor. IEEE Transactions on Nuclear Science, 37, 1571-1577.
- Imbert, C., Berton, J.L. and Gimenez, N. (1996) Realization of Ultrasonic Images of Immersed Metallic Structures Using a Digital Beam Forming System. Experimental Study. Proceedings of the 1996 IEEE Ultrasonics Symposium, San Antonio, 3-6 November 1996, 765-770.
- Song, S.-J., Shin, H.J. and Jang, Y.H. (2002) Development of an Ultra Sonic Phased Array System for Nondestructive Tests of Nuclear Power Plant Components. Nuclear Engineering and Design, 214, 151-161.
- Yang, P., Chen, B. and Shi, K.-R. (2006) A Novel Method to Design Sparse Linear Arrays for Ultrasonic Phased Array. Ultrasonics, 44, 717-721. http://dx.doi.org/10.1016/j.ultras.2006.05.131
- Martin, L., Pepe, D. and Dupraz, R. (2002) Lifetime Extension of the Phenix Nuclear Power Plant. Proceedings of a Technical Meeting, Cadarache, 11-15 March 2002, 83-91.
- Giraud, M., Major, P., Gros, J., Martin, L., Benoist, P. and Burat, O. (2002) Advanced and Innovative Approaches to Inspect the Phenix Fast Breeder Reactor. Proceedings of a Technical Meeting, Cadarache, 11-15 March 2002, 83-98.
- Belcher, E.O. (1999) Limpet Mine Imaging Sonar. Proceedings of the 13th Annual International Symposium on Areo Sense, Orlando, April 1999, 2-10.
- Belcher, E.O., Lynn, D.C., Dinh, H.Q. and Laughlin, T.J. (1999) Beamforming and Imaging with Acoustic Lenses in Small, High-Frequency Sonars. Proceedings of Oceans 99MTS\IEEE, Seattle, 13-16 September 1999, 1495-1499.
- Baikov, S.V., Svet, V.D. and Sizov, V.I. (2000) Experimental Investigation of the Resolution and Sensitivity of Ultrasonic Imaging Camera with an Immersion Lens. Akusticheskij Zhurnal, 46, 596-600.
- Korobov, A.I., Burov, V.A., Dmitriev, K.V. and Rumyantseva, O.D. (2012) Resonance Acoustical Spectrometry of Solids. Physical Department, Moscow State University, Moscow, 30.
- Svet, V.D., Dement’ev, D.A. and Galoutin, V.Z. (2014) On Some Problems of Ultrasonic Visualization of Objects in Liquid Metals. Proceedings of the First Russian Acoustical Conference, Moscow, 6-10 October 2014.