Received 1 July 2014; revised 23 July 2014; accepted 20 August 2014

ABSTRACT

A stationary loudness model has been built up on the basis of the former ISO 226: 1987 concerning equal-loudness-level contours. The loudness and loudness level expressions derived in the study include the same parameters as used when determining the equal-loudness-level contours of the former ISO standard. However, as an additional main idea, a loudness summation rule has been proposed in the study. Moreover, the loudness expressions have been normalised to give the same values for people who have a similar sense of hearing. It has also been found that the loudness expressions include basically two different weightings. The first weighting is a conservative frequency weighting in the domain of sound pressure level, and the second weighting consists of coefficients applied to the weighted sound pressure levels. The latter have the greatest effect on the very low-frequency range. Finally, the paper includes a new way to use the A-weighting which takes into account the compressed character of the equal-loudness-level contours at the low frequency range. This method remarkably transforms the character of the A-weighting as a measure for low-frequency environmental noise.

Keywords:

Loudness, Loudness Level, Loudness Summation, Frequency Weightings, A-Weighting, Low Frequency Noise

1. Introduction

In [1] it was shown that an equal-loudness-level contour can be calculated according to an equation of the following type:

, (1)

where is the stimulus sound pressure level, dB, and 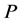(or also 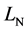when not a constant parameter) is the equal-loudness level (parameter) of the contour considered, phon. The constant 3.30 comes from S. Stevens’ power law [2] which shows that at 1000 Hz, loudness is proportional to sound intensity (sound pressure squared) according to the relation

. (2)

Additionally, in Equation (1), 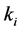(the root notation) represents the inverse of the exponent of intensity at each frequency band which has the value of 3.3 (0.3 ≈ 1/3.3) at 1000 Hz band and takes the value shown in Table 1 at the other 1/3 octave band frequencies, and finally, (in Table 1) is a frequency weighting defined in the domain of sound pressure level at each frequency band.

Both parameters and in Table 1 were determined based on the former ISO 226: 1987 [3] . The parameter 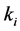was determined at each band from 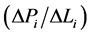because this quantity was found to be practically constant at each frequency band (the former ISO 226: 1987 and the current ISO 226: 2003 [4] differ in this respect), so that

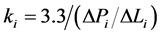. (3)

The weighting was determined from the 40-phon contour using the equation

. (4)

The equal-loudness-level contours [3] and the contours constructed according to Equation (1) are shown in Figure 1. The contour complexes are so similar that they could be replicas of each other. In [1] , the author also suggested that the method to calculate loudness or loudness level would be

, (5)

(here “lg” is log based on 10) by assuming that the loudness in different 1/3-octave bands integrate by direct adding. However, perhaps this is not the case. On the other hand, it seems prominent that Equation (5) and the former equal-loudness-level contours ISO 226 [3] have the same acoustically definable parameters and although the parameters do not exist in the former ISO 226.

However, irrespective of the similarities of the contour complexes above, no rules to connect the different frequency bands with respect to achieve the total loudness seem to be available. Therefore, some questions arise here. The questions are:

· What is the meaning of the factor 33 before the log operator “lg” and should the loudness level equation include a constant additive term?

· Does the assumed adding process work?

· What is the connection between the loudness level equation and the equations based on the A-weighted sound pressure levels?

This study attempts to give an answer to these questions. Of course, many questions remain outside this paper. These include for example: numerous time-varying effects concerning signal types in general, signal/loudness summation (time), effects of signal duration, caused adaptation, etc. In addition, critical bands (overlapping, for example) are also not considered in this paper. The latter may also have consequences on the stationary model considered here. On the other hand, however, a well-defined stationary loudness model may be necessary when developing more advanced dynamic loudness models.

2. Terms, Summation and Weightings

2.1. Factor “33”

In the following, to avoid the use of the unit “phon” and its definition [5] , we define a decibel as having a logarithmic base of two (2) including an additive constant of 40 and denote the units of such a decibel by dB₂. Then, for any positive quantity

. (6)

Thus here, clearly makes sense so far as makes sense, and unequivocally determines the defined logarithmic quantity in units of dB₂ and vice versa. Therefore, in this paper, the quantity (later also or) has been used as the primary quantity for direct loudness sensation. In particular, if happens to be a loudness function or expression [5] , the following relation between the loudness level or in phons and the loudness in sones is valid [5]

. (7)

Here the loudness level (or generally) of a sound is expressed as phons when it is judged by normal observers to be equally loud to a pure tone (or a narrow band noise) at the frequency of 1000 Hz which has the sound pressure level of decibels. In particular, the relation has been defined to hold exactly by denoting as 40 phons the equal-loudness-level contour which crosses 40 dB at the decibel axis. Additionally, the standard [5] includes the following note:

· The term phon, without a qualifying abbreviation, should be reserved for the expression of loudness levels determined by direct subjective measurement.

Moreover, the standard [6] states the following note:

· Experimental confirmation of this relation (Equation (7)) exists over the range 40 to 105 phons, and its use outside this range should be recognized as an extrapolation.

Therefore, in the following, we use the term “loudness level”, but “dB₂” as the unit of such a level defined above. Namely, in this study the direct loudness sensation S (in sones) is proportional to the subjective magnitude as estimated by normal observers and the loudness level has been defined only mathematically as stated above. Therefore, the notes in standards [5] and [6] are not restrictive in this study. In addition, some definitions are needed for reference purposes. As stated in [7] by the author, a sound in sound pressure levels (dB) at 1000 Hz (see above) is designated to represent the loudness S of one sone (=40 phons respectively). Such a sound must be defined for reference purposes (referring to normal hearing) and to fix the subjective loudness level and the loudness function unequivocally at the physical dB axis. If such a sound is designated to be a tone or narrow band noise of 40 dB at 1000 Hz frequency band (representing one sone for normal observers), the logarithmic decibel and phon coincide at 1000 Hz by definition. However, that also concerns dB_2, because the definitions of the phon and dB₂ levels do not differ at the point considered, so that

. (8)

when deriving the equal-loudness-level complexes in [1] , Stevens’ power law [2] was assumed to hold over the whole sound pressure level range. Therefore Equation (2) must be written [7] as

. (9)

Then Equation (9) is satisfied if takes the value, and as a consequence, Equation (5) takes the form

(10)

which is the same as Equation (5) and thus no additive constant is needed here. The conclusion here is: the loudness function (the direct subjective, normalised strength of auditory perception) is now (in sones) a non-lo- garithmic equation of type

. (11)

when replacing the root by, Equation (11) can be written as follows

(12)

where the last equation shows how the loudness levels in 1/3-octave bands (, dB₂) should be taken into account when the calculations are based on S. Stevens’ power law and the logarithmic definitions above.

2.2. Loudness summation

As concluded above, the actual loudness is proportional to the total sum of terms

. (13)

Then if, for example, one considers a case where only two terms exist, the sum becomes

. (14)

If, now, it happens that both bands have approximately the same loudness level value (45 dB₂ with

for example), becomes. Thus one can see that we have doubled the one single loudness value. That would mean that, in this case, the loudness level has increased by approximately 10 dB₂. However, the sound pressure level has increased by only 3 dB. Therefore some reservations arise here. Namely, based on the power law we needed 10 dB to be added to the sound pressure level at 1000 Hz to get double loudness and 10 dB₂ more in loudness level. Therefore here, we define the summation (by hypothesis) by the following rule:

. (15)

Thus, Equation (15) differs from Equation (13) in that respect that the exponent of is –(23/33) instead of zero in Equation (13). In addition Equation (15) has been written in a certain manner including an average in the last parentheses. The loudness level (dB₂) now becomes

. (16)

In the case of the sum above, one now gets having a value of which is 1.23 times the one single loudness value giving 3 dB₂ more in loudness level. By using Equation (15), (16) can also be written in the form

. (17)

A formally similar equation to Equation (17), with respect to the number of the frequency bands and average, can be written for the usual A-weighted sound pressure level, i.e.

. (18)

Thus it seems that the numerous measurements and calculations with the A-weighted sound pressure levels support the chosen summation rule (the hypothesis of the study). Then, the total summation-adjusted loudness expression, the direct subjective normalised strength of auditory perception, is finally (in sones) an equation, still non-logarithmic, of type

. (19)

Here the first factor in parentheses includes a normalising procedure giving one sone whenever the rest of the

expression takes the value of, and the second factor in parentheses with the averaging n control the

loudness summation as defined above.

2.3. The A-weighting

In [1] the author performed some comparisons between the frequent A-weighted sound pressure levels and levels which take into account Stevens’ power law. The expressions considered were respectively as follows:

(20)

, (21)

where was an abbreviation of the words Loudness Related A-weighted Level. Here the unit dB₂ as defined above has also been assumed to apply to Equation (21) and the A-weighted sound pressure level Equation (20). This helps to see behind the logarithmic total levels by determining the total loudness function using the

inverse relation between the loudness and loudness level. In such a case the loudness expression (A-wei-

ghted) from which Equation (20) has been derived is

. (22)

The respective loudness expression for Equation (21) is

. (23)

One can easily verify that the applications and give the desired dB₂-levels

shown in Equations (20) and (21). Concerning the difference between the expressions (22) and (23), only the root 3.3 has been removed with respect to the parentheses and sum, and in Equation (23) the root 3.3 does not concern the number of frequency bands. Of course, such a difference is very important [1] and on the basis of the measurements by Tachibana and his colleagues [8] - [10] , it seems that the variation of the last average in the parentheses with the exponent of 1/3.3 takes too great and uncontrolled values. Namely, in [1] the respective identities to Equations (20) and (21) were also written

, (24)

. (25)

The author [1] deduced here that in Equations (24) and (25), only the third log terms and differ and that the latter term is always smaller than the first term. Additionally, both terms are positive or equal to zero. The equality sign only appears when both terms are zero. This result supported the measurements by Tachibana and his colleagues [8] - [10] showing that the loudness level is closely related to the arithmetic mean (by adding) of the sound pressure levels. An example here was a calculation with different noises added with a 1000-Hz tone performed by Hellman and Zwicker [11] with the loudness calculations based on the standard ISO 542B [5] (and partly supported by subjective measurements). The data for broad band noise (BBN) in the frequency range 100 - 7000 Hz with the tone (Tone) are listed in Table 2.

The results [11] concerning pink noise and added different tones are shown in Figure 2, showing that the loudness of the tone-noise complexes and the respective A-weighted total sound pressure levels (Equations (20) and (24)) are partly negatively correlated.

The same figure has been repeated (Figure 3) when replacing the A-weighted sound pressure level by the level expression according to Equation (25), the only difference with respect to Equation (23) being that the power law has been taken into account in the third log term. The difference between Figure 2 and Figure 3 is dramatic. In particular, in Case 2, the difference between and is very large: the values are 18.7 and 4.6 dB₂ respectively and the difference becomes 14.1 dB₂. On the other hand, in Case 7, the respective values are 3.1 and 1.0 dB₂ with a difference of only 2.1 dB₂. The conclusion here is that the A-weighting would correlate much better with loudness if the power law was taken into account when assessing noise in general (see the order of the case points (x-axis) in Figure 2 versus in Figure 3).

In terms of loudness, the respective levels according to Equations (16) or (17) become as shown in Figure 4. The deviations from a straight line in Figure 4 are also small, but cannot separate Cases 1, 4 and 6. That seems to occur because of the same broad band noise spectrum in these cases. The respective tones are 76, 81 and 86 dB, which is not enough to separate the levels with respect to loudness. If the tone was removed from the 1000 Hz to 200 Hz frequency band, the respective levels were 87.6, 88.1, and 88.8 dB₂. The reasons for these deviations can be explained by writing for an equation similar to Equation (24) or (25), i.e.

. (26)

Equation (26) has generally similar properties to Equation (25). However, the main part of the loudness level consists of the first sum/average (a linear sum with the coefficients) and. The third log term is such that it takes the value zero if the spectrum coincides with an equal-loudness-level contour within the whole frequency band range (bands) under consideration. On the other hand, now the total loudness level includes two frequency weightings: the first weighting is the conservative -weighting in the domain of sound pressure level and the second weighting is a coefficient concerning the weighted terms. The coefficient takes the values from 1.90 to 1.00 and the maximum values appear at the lowest frequencies. Therefore, the tones separate more effectively in the low-frequency range. In particular, this is of great importance when assessing low-frequency noise. Finally, the double-weighting property of Equation (26) vs Equation (25) has a dramatic consequence: none of the equal-loudness-level contours is an inverse frequency weighting of a known or defined frequency weighting alone (A-weighting concerning 40-phon, for example).

In [12] Schomer stated: “The hypothesis to this paper is that the equal-loudness-level contours can be used as a dynamic weighting function that varies with frequency and level.” However, when taking into account the above statement concerning the double-weighting, this hypothesis does not make sense, and it must be rejected. In fact, Schomer did not define any weighting but only determined the loudness levels using the equations given in the former ISO 226 [3] . Schomer also suggested calculating the overall phon level from 1/3-octave band phon levels by summation on an energy basis. In this paper the summation is based on the power law. Therefore, Schomer’s overall phon levels differ from the levels calculated in this study in such a way that the following applies:

(27)

which can be easily verified using Equations (12), (22) and (23), for example.

Finally, because the comparison of the different equal-loudness-level contours with the frequency weightings applied to sound pressure levels does not make sense, a new way to apply the A-weighting is achieved by replacing the -weighting in Table 1 by the A-weighting. Then, the A-weighted loudness/annoyance function from Equation (19) becomes

, (28)

and the respective levels from Equation (16) become

. (29)

Here, Equations (28) and (29) are based on a similar structure to the equations concerning loudness and loudness levels. Only the weighting has been changed to the A-weighting, because this weighting is mostly used when assessing noise from the annoyance point of view. Because of the similarities to the terms in the former ISO 226 [3] , the equal loudness/annoyance level contours can now be constructed (maintaining the compressed character of the equal-level contours in the low-frequency range) using Equation (1) above. In Figure 5, the 40-phon contours [3] and [4] have been drawn. The 40-dB₂(A) equal-level contour (the A-weighting replacing the fixed frequency weighting derived for the former ISO 226 [3] ) has been drawn in the same figure.

One can see that the most severe (or the most sensitive) contour, in particular in terms of the low-frequency range, is the contour including the A-weighting which replaces the frequency weighting in an auditory perception system. At the high-frequency range the respective sensitiveness remains unchanged because of the small values of the coefficients. Finally, one may suggest that the system has no singularity below the 20 Hz frequency band. Rather, the system continues to the left. Therefore, the new way of applying the A-weighting may also render it suitable for assessing very low-frequency noise from, for example, wind turbines [13] .

3. Conclusions

A loudness or a loudness level function requires that it is normalised so that it gives the same loudness value and loudness level for people who have similar (normal) hearing. In the study, a certain logarithmic base of two was used with an additive constant of 40 dB₂ when determining the loudness levels, and the levels were only used for numerical assignment (separated from the direct loudness sensation which is seen as non-logarithmic

through out the whole study) in the way that we use decibels for characterising the sound pressures. The logarithmic base was chosen on the basis of Stevens’ power law and gave the first final result (Equation (10)) that the derived loudness level does not need any additive constant in this respect.

As regards loudness summation it was stated that loudness or a loudness level expression includes a main problem of how to proceed when connecting the loudness values at different frequency bands. The problem is important because, in practice, the number of the frequency bands has to be a variable. In the study the hypothesis was that when applying a direct summation of loudness at each frequency band, the number of the frequency bands has too great an effect on the final result. Therefore, the exponent of the number of bands in a loudness expression has to take a negative value instead of zero in the direct summation process. The exponent value has been chosen (by hypothesis) to be –23/33 in this study. The proposed method was supported by the finding that the A-weighted total sound pressure level formally includes a similar summation rule. Lacking subjective data, this rule has not been otherwise tested in the study. However, this was the second main result (Equation (16) and (17)) of the study.

It was also shown that the expression of loudness and loudness level expressions can be written as identical formulas so that one can separate some essential parts which finally define the behaviour of the whole loudness system and expressions. The third main result (Equation (26)) revealed that the total loudness level includes two frequency weightings of different types: the first weighting is a conservative weighting in the domain of sound pressure level, and the second weighting is a coefficient applied to the weighted sound pressure level terms. Finally, the double-weighting property of the auditory perception system seemed to have a surprising consequence for loudness and loudness levels: none of the equal-loudness-level contours is an inverse frequency weighting alone.

Finally, because the comparison of the different equal-loudness-level contours with the frequency weightings did not seem to make sense, a new way of applying the A-weighting for annoyance purposes was proposed which entailed replacing the loudness system weighting by the A-weighting. Then it was found that the most severe 40-phon (or 40-dB₂) contour, for example, in particular as regards the low-frequency range, is the contour derived on the basis of the A-weighting. This was the final main result (Equation (29)) of the study.

References