Open Journal of Acoustics
Vol.3 No.1(2013), Article ID:29321,7 pages DOI:10.4236/oja.2013.31002
Some Aspects of Ray Representation Running Sound Waves in Liquid Spaces
Institute of Applied Physics, Russian Academy of Sciences, Nizhny Novgorod, Russia
Email: ivg@hydro.appl.sci-nnov.ru
Received November 15, 2012; revised December 24, 2012; accepted December 31, 2012
Keywords: Sound Running Waves; Wave Equation; Reflection; Passage; Liquid Space; Wave-Guide; Rays
ABSTRACT
Work is devoted to the analysis of errors meeting in literature in treatment of a spatial part of a phase of running sound waves. In some cases, it is not taken into consideration that this part of a phase is formed by scalar product of vectors which does not depend on a choice of system of co-ordinates. Taking into account the necessary corrections in record of a phase of plane waves, it is shown that the decision of the homogeneous wave equation in the form of “belated” potentials is simultaneously and the decision of the equations of movement of a liquid, and “outstripped” potentials does not satisfy them. The analysis of coefficients of reflection and passage of running waves in non-uniform space is carried out. It is shown that on boundary of spaces with different sound speeds, a turning point of a sound wave is the point of full internal reflection. The way of calculation of coefficients of reflection and passage is offered by consideration of all three waves on boundary of spaces as vectors with the set directions and amplitude of a falling wave. Calculation of coefficients of reflection and passage of a sound wave in a wave-guide of canonical type along the chosen trajectory by two methods—under traditional formulas and a vector method is carried out. Results of calculation practically coincide.
1. Introduction
The most widespread acoustics of ocean is representation of a sound wave in the form of a running wave along a trajectory (ray). It is a ray method description of sound waves in a liquid. Among modern computing means, the ray method of calculation of a sound field does not cause any difficulties. Advantage of this method consists that it contains a minimum quantity assumptions and can serve as the standard for an estimation of other methods. It proves to be true, for example, calculation of a sound field in the area of caustics [1-3]. Before development of the machine account the total field in area of caustics calculated approximately by means of introduction of the modeling factor of focusing [4]. Unique restriction of the use of a ray method is performance of conditions of geometrical acoustics in non-uniform spaces [5].
In the given work, the running sound waves created in the non-uniform water space by a point isotropic monochromatic source are considered. It is obvious that it is possible to present a field of such source as a set of the fields extending along trajectories and having various angles of departure from a source. Calculation of a trajectory for any angle of departure in the non-uniform space is spent by means of Snell’s law. As is known, the phase of a running wave at its propagation remains invariable. In the literature, there is an erroneous interpretation of a spatial part of the wave’s phase, leading in some cases to incorrect physical conclusions [4-7].
The purpose of the given work consists of the following: explanation of the reasons of a wrong writing of a spatial part of a phase of a running wave, elimination of mathematical errors in its records and change of physical treatments of separate well-known results. It concerns the use of the wave equation at research of propagation of sound waves in liquids, a way of reception of coefficients of reflection (CR) and passage (CP) sound waves in works [4-7], and their dependence on an angle of departure of sound wave’s trajectories from a source. The vector method of reception CR and CP on boundary of two homogeneous spaces, based on representation of each wave by a vector with a known direction of propagation is offered. Calculation of CR and CP, received by two methods, along a trajectory of a sound wave in a wave-guide of canonical type is carried out.
2. Phase as the Basic Characteristic of the Running Sound Wave
The field of the running sound wave created by a monochromatic dot source, in the ray theory is given by following expression:
 (1)
(1)
In Equation (1) it is accepted, that a plane of falling of a sound wave 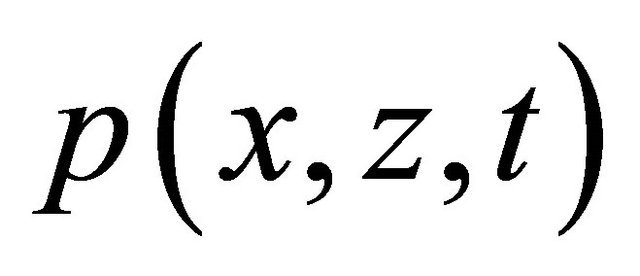 is the plane
is the plane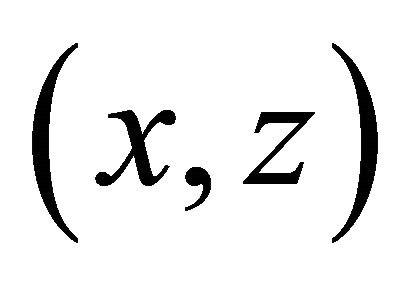 , A—amplitude of a wave, ψ—a wave phase (eikonal), consisting of 2 components: kR—a spatial part, ωt—a time part. In a spatial part of a phase k—a wave vector, its module
, A—amplitude of a wave, ψ—a wave phase (eikonal), consisting of 2 components: kR—a spatial part, ωt—a time part. In a spatial part of a phase k—a wave vector, its module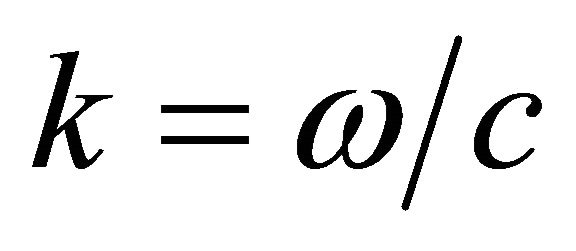 , c—a sound speed in a liquid, R—a vector along the wave trajectory, coinciding with a vector direction k in any point of a trajectory. Propagation time of a wave t is equal
, c—a sound speed in a liquid, R—a vector along the wave trajectory, coinciding with a vector direction k in any point of a trajectory. Propagation time of a wave t is equal , R—the module of vector R, ω—frequency of radiation of a source. Let’s consider the sound field radiated by a source in a homogeneous space in a direction of a wave vector k. As is known, in a homogeneous spaces a vector k—the constant, its length k (value of module) and a direction are invariable. The length of vector R (module R) grows at wave propagation, its direction also invariable.
, R—the module of vector R, ω—frequency of radiation of a source. Let’s consider the sound field radiated by a source in a homogeneous space in a direction of a wave vector k. As is known, in a homogeneous spaces a vector k—the constant, its length k (value of module) and a direction are invariable. The length of vector R (module R) grows at wave propagation, its direction also invariable.
In acoustics of ocean the distance and time of propagation of sound waves have the basic interest. Just on these values it is possible to judge about the various phenomena at sound propagation at ocean. Therefore to their calculation the paramount attention is spared. In the course of propagation both parts of a phase of a running wave vary simultaneously, than the phase constancy ψ (eikonal) is provided. This is a basic property of a phase of a running wave. According to definition of scalar product of two vectors in its size the scalar product is value which is not dependent on a choice of system of co-ordinates in which both vectors are presented [8,9]. In a liquid a spatial part of a phase 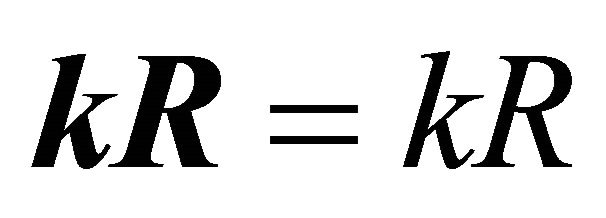 since vectors are parallel each other. Each vector has the length and a direction. The vector k has the length (module) equal
since vectors are parallel each other. Each vector has the length and a direction. The vector k has the length (module) equal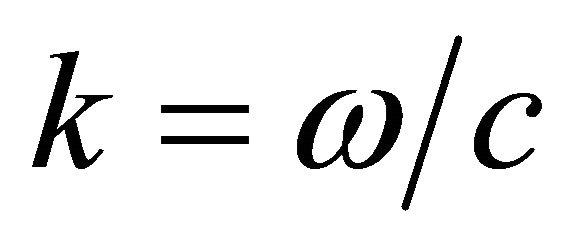 , depending on co-ordinates if the space is non-uniform. The length of vector R (its module R) is defined its initial and final (current co-ordinate) by reference points.
, depending on co-ordinates if the space is non-uniform. The length of vector R (its module R) is defined its initial and final (current co-ordinate) by reference points.
There are various forms of record of scalar product kR. Let’s present product of parallel vectors kR through their modules (lengths) k, R. We will enter a single vector n, coinciding with a direction of vectors k, R:
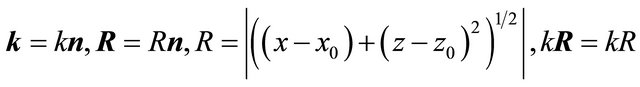 (2)
(2)
Here 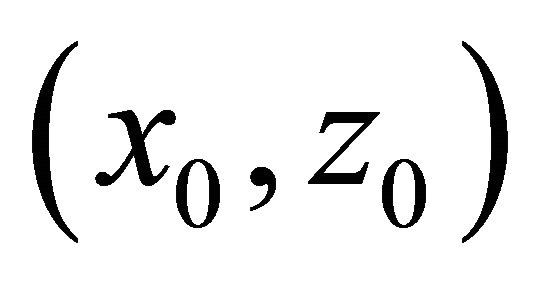 co-ordinates of an initial point of readout of vector
co-ordinates of an initial point of readout of vector 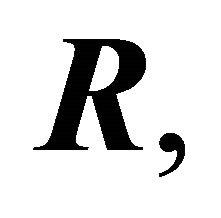
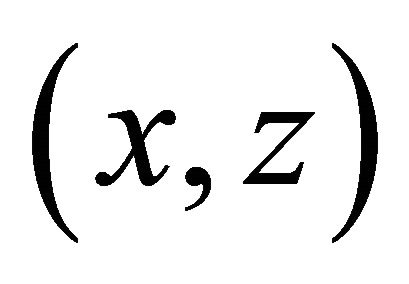 —its final (current) co-ordinates. Vector’s orientations concerning the chosen system of co-ordinates don’t enter in expression (2). This means that scalar production of parallel vectors k, R is positive member always and don’t depend from choice of system of co-ordinates.
—its final (current) co-ordinates. Vector’s orientations concerning the chosen system of co-ordinates don’t enter in expression (2). This means that scalar production of parallel vectors k, R is positive member always and don’t depend from choice of system of co-ordinates.
There is a set of problems in which it is studied dependence of several functions from an angle of wave’s propagation, for example, the wave’s reflection and passage. In these cases there is used the combined way of record kR. In it projections of a wave vector k are expressed through its module and an angle θ between a vector and an axis z on a plane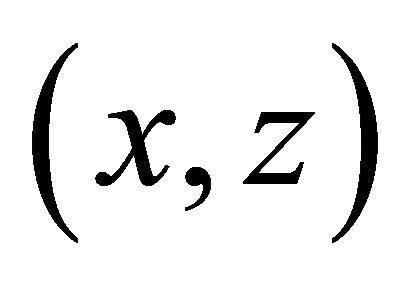 , and projections of vector R in length of projections of a vector on an axis x, z:
, and projections of vector R in length of projections of a vector on an axis x, z:
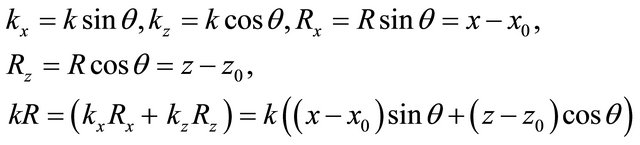 (3)
(3)
At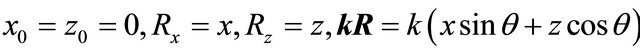 .
.
In that form of record scalar production kR includes an angle θ that shows vector’s orientations concerning the chosen system of co-ordinates. Exchange 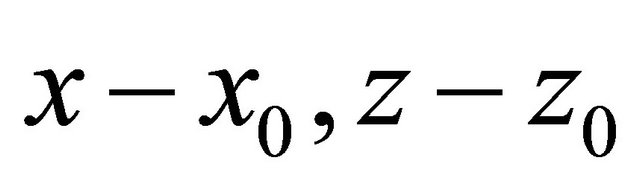 on their expressions through θ, R we get that
on their expressions through θ, R we get that 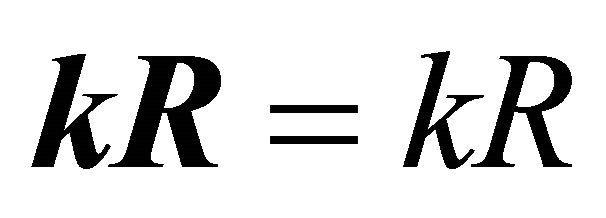 as in (2). It is obviously that parallel vectors have projections on an axis of co-ordinates of identical sign: If
as in (2). It is obviously that parallel vectors have projections on an axis of co-ordinates of identical sign: If
 then
then
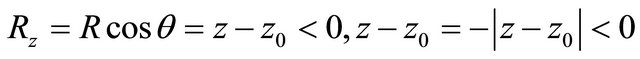 signs kz,Rz are negative and product
signs kz,Rz are negative and product 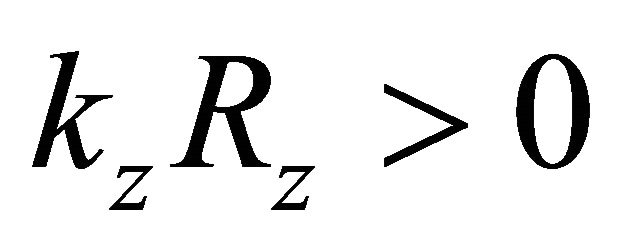 always. Thus, in two forms of record scalar product of parallel vectors kR is expressed through their modules (lengths) and does not depend on orientation of vectors k,R concerning the chosen system of co-ordinates.
always. Thus, in two forms of record scalar product of parallel vectors kR is expressed through their modules (lengths) and does not depend on orientation of vectors k,R concerning the chosen system of co-ordinates.
Let’s note one more important property of a phase of a running wave. Any additions in wave’s phase are inadmissible if they do not connect with change of vectors k and R. Such additions break periodic structure of a sound field along a trajectory and simple connection of spatial and time components of eikonal. If addition in phase ~>π then the use of geometric acoustic is invalid.
3. Decition of the Wave Equation for the Running Sound Waves in Liquid
It is known that the linear differential equations of movement of a liquid for definition of functions of oscillatory speed of particles of a liquid and pressure can be reduce to the wave equation in the homogeneous, isotropic environment. It can be carried out in two ways: or to express one function through another, or to enter the wave potential, satisfying to the wave equation through which pressure and oscillatory speed of a liquid are expressed. In many works, for example, in [5,7] for sound waves and in [10] for electromagnetic waves, possibility of a finding of required functions by means of the decision of the homogeneous wave equation is considered. For simplification is accepted, that the required decision of the wave equation is a plane wave which have only one spatial co-ordinates, for example, x, and time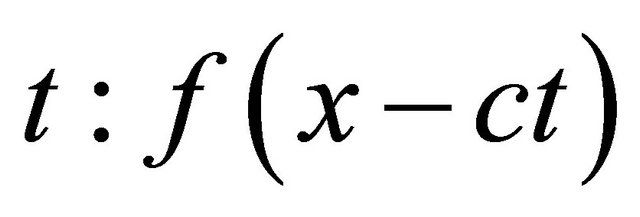 . In [5,7,10] it is received, that the decision of the wave equation in these variables consists of two any functions of arguments
. In [5,7,10] it is received, that the decision of the wave equation in these variables consists of two any functions of arguments
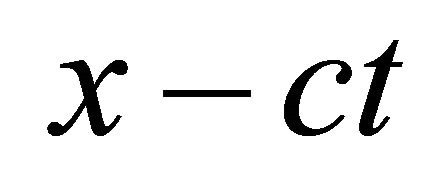 and
and :
:
 (4)
(4)
In [10] it is shown, that Maxwell’s equations have only one function as decision. Obviously, occurrence of the second function in the decision of the homogeneous differential equation of the second order for field potentials is caused by increase of an order of the differential equation from which potentials are defined. In [10] it is offered to exclude the second decision of the wave equation, function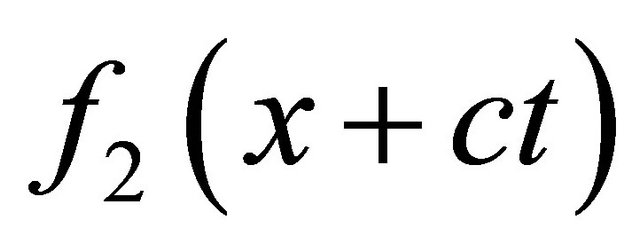 , “outstripped” potentials. It is suggested to entry beginning conditions in the form of “belated” potentials,
, “outstripped” potentials. It is suggested to entry beginning conditions in the form of “belated” potentials, 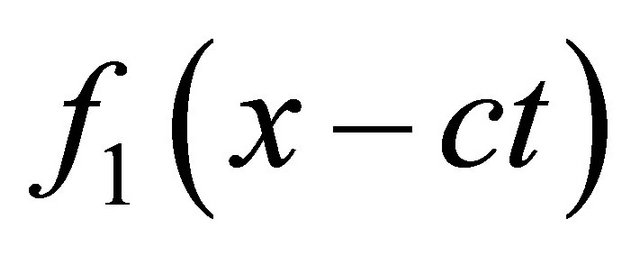 , and boundary conditions, in [8] last are called as limiting conditions. These two conditions do the decision of the non-uniform wave equation equal to
, and boundary conditions, in [8] last are called as limiting conditions. These two conditions do the decision of the non-uniform wave equation equal to  only.
only.
In [5,7] is accepted, that both functions f1 and f2 satisfy to the equations of movement of a liquid: f1 corresponds to a plane running wave in a positive direction of an axis x, function f2 – represents the plane wave extending in a negative direction of an axis x. Expressions  represent phases of waves
represent phases of waves
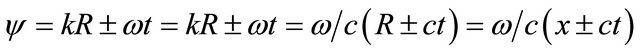 because vector
because vector , the plane wave runs along axis x, vector too,
, the plane wave runs along axis x, vector too, . It is shown higher that
. It is shown higher that 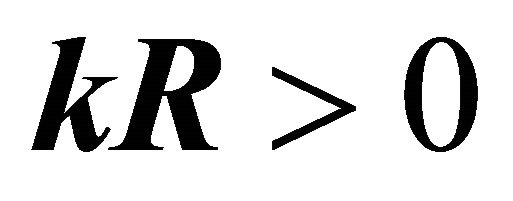 always. The value x in arguments f1, f2 must be module x otherwise x ± ct is the sum of vector and scalar. Put
always. The value x in arguments f1, f2 must be module x otherwise x ± ct is the sum of vector and scalar. Put 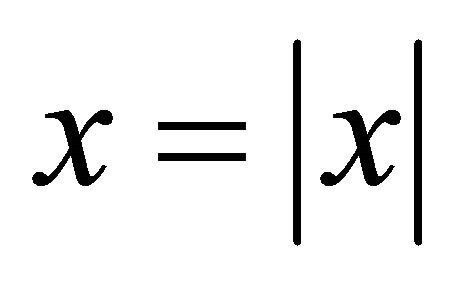 we may consider functions f1 and f2 as “belated” and “outstripped” potentials of a plane running wave. With these arguments function f1 can describe a plane running sound wave in any direction of an axis x, and f2 may be exclude with beginning conditions. Function f2 has appeared as a result of transition from system of the differential equations of 1st order to the wave equation of 2nd order. Besides it is easy to show, that function
we may consider functions f1 and f2 as “belated” and “outstripped” potentials of a plane running wave. With these arguments function f1 can describe a plane running sound wave in any direction of an axis x, and f2 may be exclude with beginning conditions. Function f2 has appeared as a result of transition from system of the differential equations of 1st order to the wave equation of 2nd order. Besides it is easy to show, that function
 , chosen as initial function for speed of movement of particles vx (or for pressure p) after substitution in the equations of movement of a liquid gives the following communication of pressure and speed:
, chosen as initial function for speed of movement of particles vx (or for pressure p) after substitution in the equations of movement of a liquid gives the following communication of pressure and speed: , ρ— density of space. It means that speed of movement of particles and pressure vary in an anti-phase that is incurrect. Use as initial function f1 yields correct result:
, ρ— density of space. It means that speed of movement of particles and pressure vary in an anti-phase that is incurrect. Use as initial function f1 yields correct result: . This one more acknowledgement of that function
. This one more acknowledgement of that function 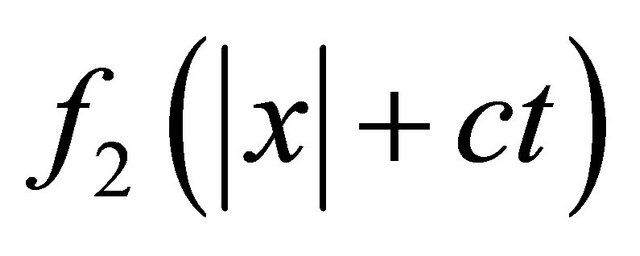 is not necessary to take into consideration, since its occurrence—a consequence of the spent mathematical operations.
is not necessary to take into consideration, since its occurrence—a consequence of the spent mathematical operations.
In [5] decision of the wave equation in the form of Equation (4) is used for an illustration of formation of a standing wave in a liquid at propagation of two plane waves defined by functions f1 and f2, and extending along an axis x in opposite directions. We will show, that the standing wave can be received, not using the decision (4). In [11] the way of reception of a standing wave by means of two coherent waves, identical intensity extending towards each other is offered. Coherent waves are created with that they represent earlier and later parts of the same wave. The contrary wave is formed by well reflecting screen. For formation of a standing wave it is necessary to describe both waves one function f1 in Equation (4), in which . We will assume, that the source of a continuous sound wave is in the beginning of co-ordinates, x0 = 0. In a point x = L completely reflecting screen is placed. Let’s consider a sound field in any point x < L, formed by the contrary waves, one of which left a source during the moment t = 0, has reached the screen, was reflected from it and has reached a point x, moving in an opposite direction. Other wave left a source during the moment
. We will assume, that the source of a continuous sound wave is in the beginning of co-ordinates, x0 = 0. In a point x = L completely reflecting screen is placed. Let’s consider a sound field in any point x < L, formed by the contrary waves, one of which left a source during the moment t = 0, has reached the screen, was reflected from it and has reached a point x, moving in an opposite direction. Other wave left a source during the moment  and moves towards to the wave reflected from the screen.
and moves towards to the wave reflected from the screen.
We will receive the sum of two waves at a point x at the moment of time t:
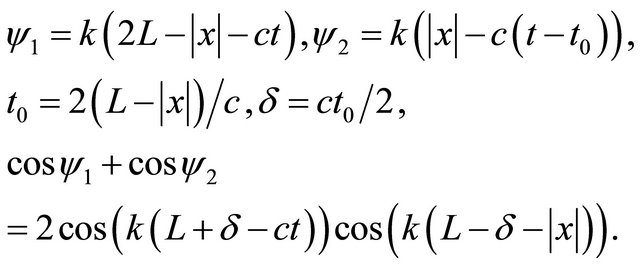 (5)
(5)
It is obvious, that the received expression (5) is a standing wave.
4. Reflection and Passage Coefficients on Boundary of Two Spaces
Calculation of coefficients of reflection and passage is based on representation of a sound wave in the liquid space in the form of a running wave along a trajectory (ray). We will analyse a way of reception of coefficients of reflection (CR) and passage (CP) the sound waves, resulted in works [4-7], and their dependence on a falling angle. At calculation CR and CP in [4-7] it is accepted, that the liquid space consists of two homogeneous semispaces with density and speeds of a sound ρ, c and ρ1, c1 above and below the boundary of spaces parallel to an axis x. The sound source is in the space with parameters ρ, c. The scheme of an arrangement of sound waves near to boundary is shown on Figure 1. In [4,6] it is accepted, that the amplitude of a falling wave is equal 1. Then amplitudes of the reflected and passed waves coincide with coefficient of reflection V and passage W. Boundary conditions for a finding V and W, used in [4-6], look like:
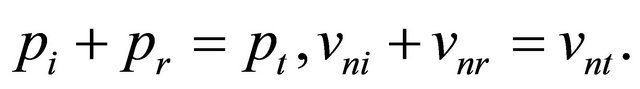 (6)
(6)
Here pi, pr, pt—pressure, vni, vnr, vnt—normal components oscillatory speeds of a liquid in the falling, reflecting and passed waves. Sound pressure upon boundary of spaces register in [4] at an exception of a time part of a phase in a kind:
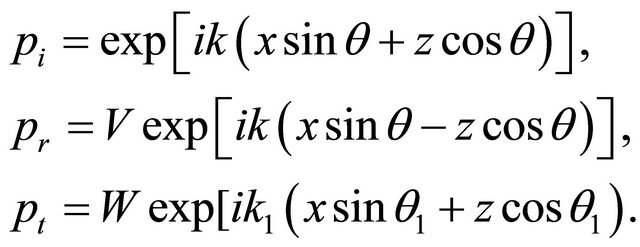 (7)
(7)
In Equation (7) it is taken, that modules 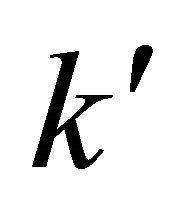 and
and 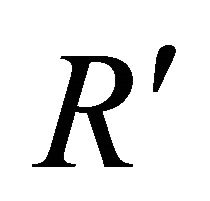 on Figure 1 coincide with k and R, θ and θ1—angles under which the falling and passed waves extend,
on Figure 1 coincide with k and R, θ and θ1—angles under which the falling and passed waves extend, 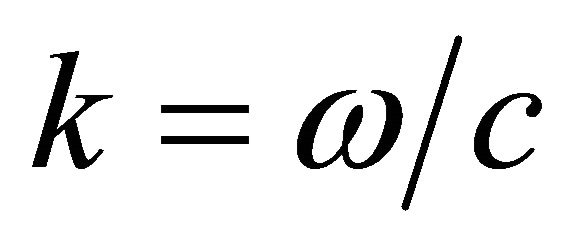 and
and 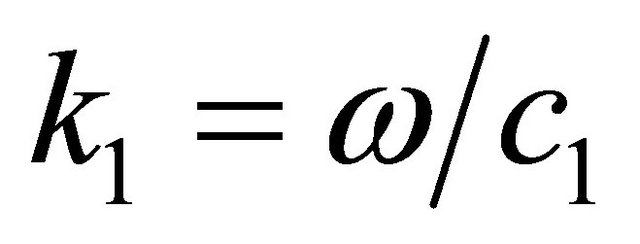 modules of their wave vectors. For calculation CR and CP, according to boundary conditions (6), coincidence of phases of all three waves on boundary is necessary. If this conditions carry out the continuity of oscillatory process in a liquid will be guarantee at occurrence of two new waves-reflected from boundary and passed through it. For performance of this condition on boundary of division the initial phase of the reflected wave should coincide with a phase of a falling wave, the initial phase z-components of the passed wave should be equal to a phase z-components of a falling wave. According to Snell’s law phases x-component of the falling and passed waves coincide. At performance of these conditions phases of all three waves coincide on boundary of division z and are excluded from boundary conditions (6). As follows from Equation (7), signs z-component of scalar product of the falling and reflected waves do not coincide. According to Equations (2) and (3) it is wrong. The error has resulted from use in Equation (7) combined ways of record kR—vector projections k are expressed through its module k and an angle θ, and vector R through its projections to axes of co-ordinates x and z. In [8] it is noticed, that such form of record of scalar product makes impression about dependence kR from orientation of vectors k, R concerning axes. In Equation (7) z-component of scalar product of the reflected wave is negative. It means, that the sign of one of z-components of vectors k’, R’ is not changed on (−), agrees Figure 1. Therefore their product kzRz became negative. Correction of this error leads to that the phase of the reflecting wave in Equation (7) on boundary coincides with a phase of a falling wave:
modules of their wave vectors. For calculation CR and CP, according to boundary conditions (6), coincidence of phases of all three waves on boundary is necessary. If this conditions carry out the continuity of oscillatory process in a liquid will be guarantee at occurrence of two new waves-reflected from boundary and passed through it. For performance of this condition on boundary of division the initial phase of the reflected wave should coincide with a phase of a falling wave, the initial phase z-components of the passed wave should be equal to a phase z-components of a falling wave. According to Snell’s law phases x-component of the falling and passed waves coincide. At performance of these conditions phases of all three waves coincide on boundary of division z and are excluded from boundary conditions (6). As follows from Equation (7), signs z-component of scalar product of the falling and reflected waves do not coincide. According to Equations (2) and (3) it is wrong. The error has resulted from use in Equation (7) combined ways of record kR—vector projections k are expressed through its module k and an angle θ, and vector R through its projections to axes of co-ordinates x and z. In [8] it is noticed, that such form of record of scalar product makes impression about dependence kR from orientation of vectors k, R concerning axes. In Equation (7) z-component of scalar product of the reflected wave is negative. It means, that the sign of one of z-components of vectors k’, R’ is not changed on (−), agrees Figure 1. Therefore their product kzRz became negative. Correction of this error leads to that the phase of the reflecting wave in Equation (7) on boundary coincides with a phase of a falling wave:
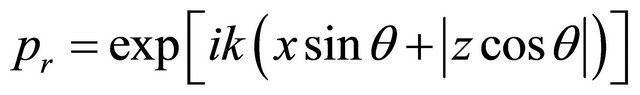 (8)
(8)
In works [4,6] direction of an axis z opposite accepted on Figure 1. Therefore a sign (−) at z-components of scalar product have phases of the falling and passed waves,
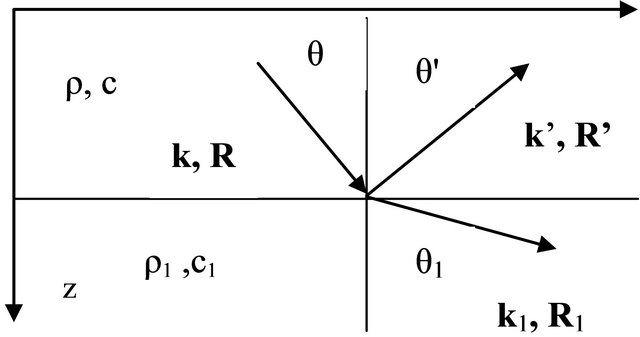
Figure 1. Scheme of disposition sound rays.
and it should be replaced on (+). In the reflected wave z-component is positive.
The sign (−) in one of composed scalar product contradicts the main property of a running sound wave—the spatial part of a phase always grows, (grows R), irrespective of change of a direction of propagation of a wave, since component’s signs of k and R on axes of coordinates vary simultaneously. In a real waveguide for a full cycle of a trajectory, we will designate it D, the sound wave crosses a waveguide between turning points twice, thus, according to Equation (7), z-components of scalar product kR have different signs. In such record the size kR along the whole cycle is defined only by length of cycle D as no displacement of a trajectory on depth is present. As a result the error in a sign on one of components kR leads to distance reduction (and propagation time), passed by a wave.
Authors [4,5,7], for an exception in (7) phases of sound waves have accepted, that the boundary of spaces lays on depth z = 0. We will show, that this condition does not exclude phase component kzRz on boundary. Actually, according to Figure 1 for the falling wave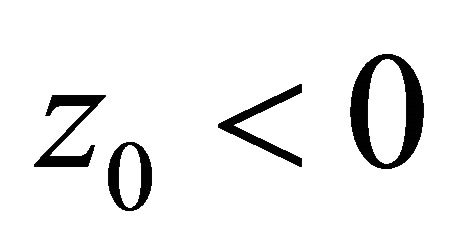 , at boundary
, at boundary ,
,  ,
,
 , for reflecting wave
, for reflecting wave ,
,
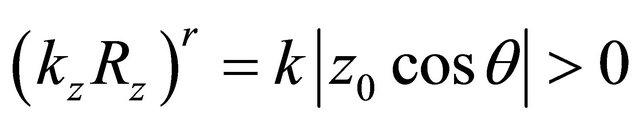 . As seen from Equation (7), phases of sound waves on boundary in a point
. As seen from Equation (7), phases of sound waves on boundary in a point  must be equal:
must be equal:
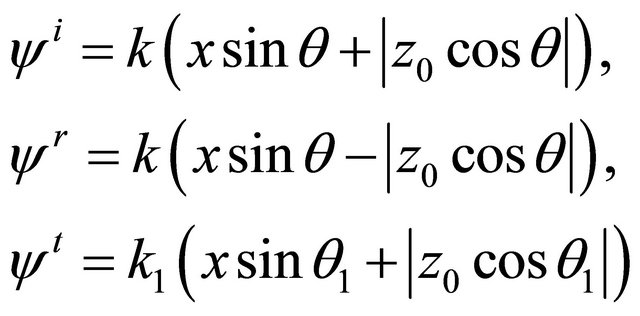 (7’)
(7’)
According to (7’) the boundary condition for pressure (7) will become:
 (6')
(6')
In Equation (6’) is present a phase of a sound wave, in such form the boundary condition (6’) cannot be used for definition of coefficients V and W.
The boundary condition (6) for pressure with the account Equation (8) takes a form, as well as in [4,6]:
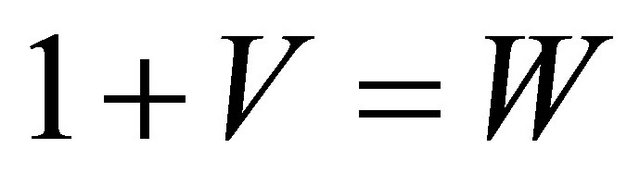 (6")
(6")
In [4-6] normal components of speed vn is defined as a gradient of pressure. Scalar production kR = kR don’t include directions vectors k, R relatively axis co-ordinates. It is known from decision equations of movement of liquid that  and direction v coincides with directions k, R, which is known from initial conditions. According Figure 1 amplitudes of normal components of speeds are equal:
and direction v coincides with directions k, R, which is known from initial conditions. According Figure 1 amplitudes of normal components of speeds are equal:
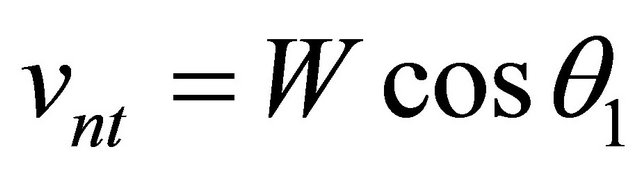
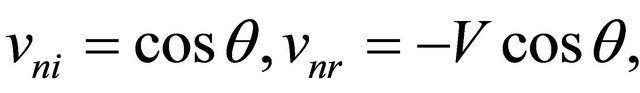 .
.
As a result of substitution of amplitudes 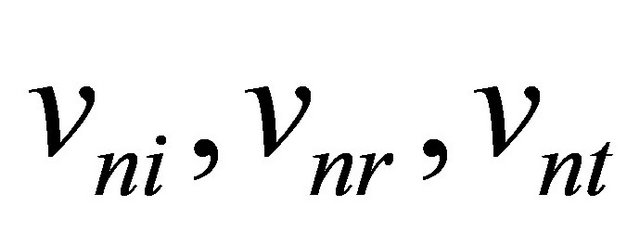 to Equation (6) a boundary condition for normal component of speeds coincides with resulted in [4,6,7]:
to Equation (6) a boundary condition for normal component of speeds coincides with resulted in [4,6,7]:
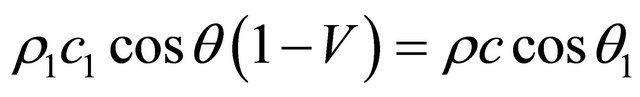 (9)
(9)
From parities (6") and (9) we will receive formulas for V and W, coinciding with showed in [4,6,7], but fair for any depth of boundary of spaces:
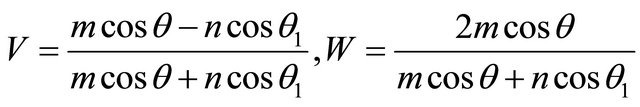 (10)
(10)
Here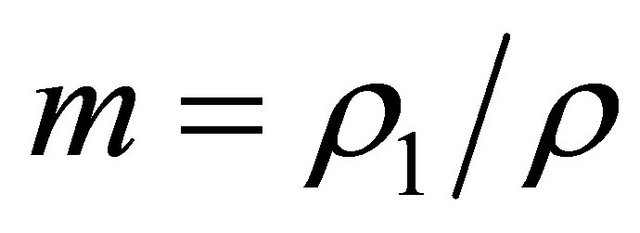 —the relation of densities,
—the relation of densities, — refraction coefficient on boundary of spaces
— refraction coefficient on boundary of spaces
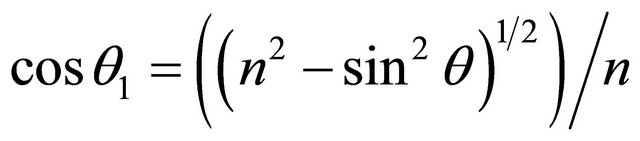 according to Snell’s law.
according to Snell’s law.
Let’s consider sizes V and W for the most important cases. It is known, that in water . The CR V at reflection from boundary water—air is close to (−1), and CP W—to 0. The value V equal (−1) in [4] is considered admissible and is used at construction mode models of propagation of a sound in waveguides. However,
. The CR V at reflection from boundary water—air is close to (−1), and CP W—to 0. The value V equal (−1) in [4] is considered admissible and is used at construction mode models of propagation of a sound in waveguides. However, 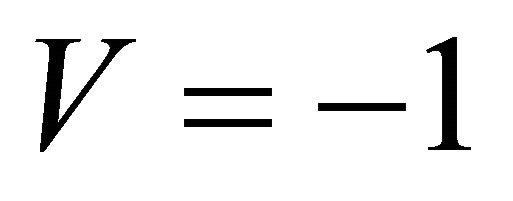 contradicts formulas (7) where V and W play a role of amplitudes which always >0. At
contradicts formulas (7) where V and W play a role of amplitudes which always >0. At 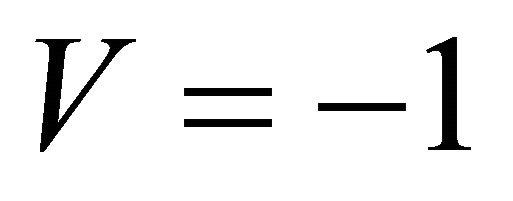 the continuity of oscillatory process for pressure and speed of particles is broken, since sign change before a sound wave
the continuity of oscillatory process for pressure and speed of particles is broken, since sign change before a sound wave , Equation (1), is identical to change of a phase of a wave on π. At such change of a phase on boundary of spaces without distance change (z does not vary) approach of geometrical acoustics is inapplicable.
, Equation (1), is identical to change of a phase of a wave on π. At such change of a phase on boundary of spaces without distance change (z does not vary) approach of geometrical acoustics is inapplicable.
Let’s consider a situation, when a refraction coefficient between spaces n < 1, [4,6]. When sinθ = n, according to Snell’s law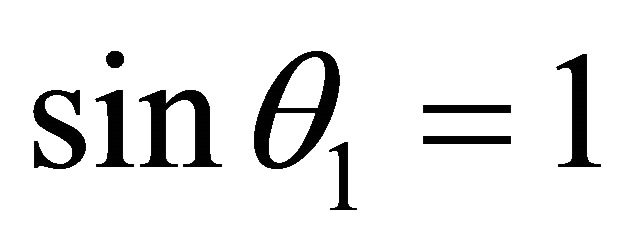 , i.e.
, i.e. . Then from (10) follows, that V = 1, and W = 2. An angle of departure at which sinθ = n is designated θcr and. is called critical or an angle of full internal reflection (FIR). At θ = θcr there is a full reflection (turning) a falling sound wave towards a source since at
. Then from (10) follows, that V = 1, and W = 2. An angle of departure at which sinθ = n is designated θcr and. is called critical or an angle of full internal reflection (FIR). At θ = θcr there is a full reflection (turning) a falling sound wave towards a source since at 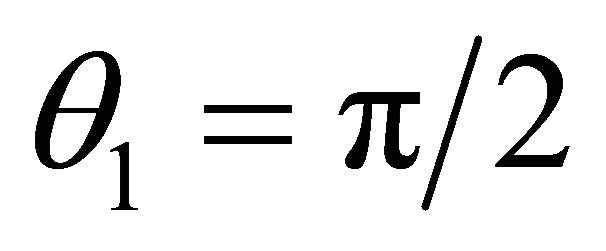 normal component of speed
normal component of speed 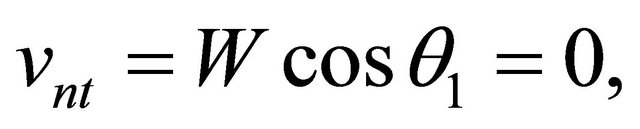 the passed sound wave does not cross boundary of spaces. Thanks to that V = 1, the last wave does not extend and along an axis x. Thus, at
the passed sound wave does not cross boundary of spaces. Thanks to that V = 1, the last wave does not extend and along an axis x. Thus, at 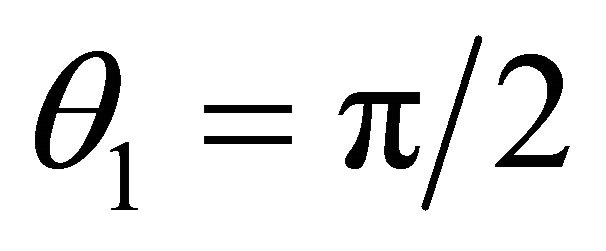 the trajectory does not become horizontal as it is considered to be, see, for example, [4,12]. The wave is reflected from boundary under an angle
the trajectory does not become horizontal as it is considered to be, see, for example, [4,12]. The wave is reflected from boundary under an angle  towards a source. It leads to reduction of a range of possible values θ along a trajectory in oceanic wave-guides, what, in turn, causes shortening both trajectories, and lengths of a cycle of a sound wave.
towards a source. It leads to reduction of a range of possible values θ along a trajectory in oceanic wave-guides, what, in turn, causes shortening both trajectories, and lengths of a cycle of a sound wave.
In the literature values  are in detail considered. It is accepted that at theses cases CR V becomes complex value because
are in detail considered. It is accepted that at theses cases CR V becomes complex value because
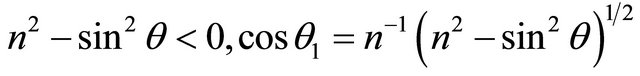
becomes imaginary value in Equation (10). According Snel’s law 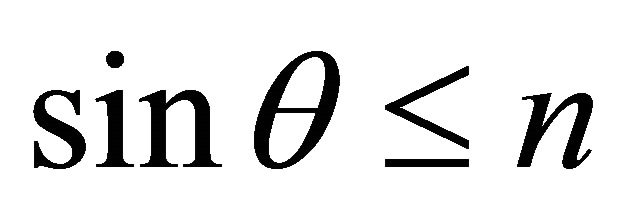 always. Because of it
always. Because of it  must be too. It means that
must be too. It means that 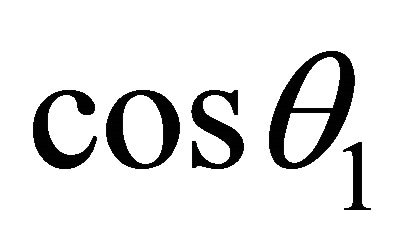 is real always. Let us show that rays with
is real always. Let us show that rays with 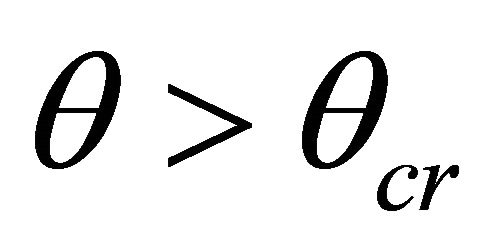 can be never at the boundary of two spaces. Usually it is supposed, that change of sound’s speed on boundary spaces with c, c1 occurs on small, but a final interval Δz on which change kR is a little, <π, differently geometrical acoustics is inapplicable. At fluent transition from boundary with sound speed c into transitional layer Δz to the space with the sound speed c1 refraction coefficient n changes from
can be never at the boundary of two spaces. Usually it is supposed, that change of sound’s speed on boundary spaces with c, c1 occurs on small, but a final interval Δz on which change kR is a little, <π, differently geometrical acoustics is inapplicable. At fluent transition from boundary with sound speed c into transitional layer Δz to the space with the sound speed c1 refraction coefficient n changes from 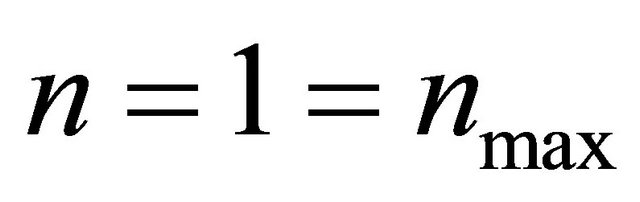 to
to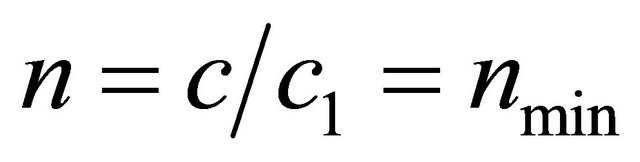 . Accordingly it is changed and
. Accordingly it is changed and 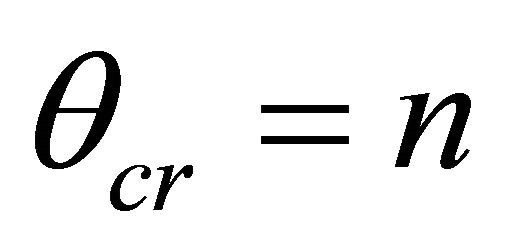 from
from 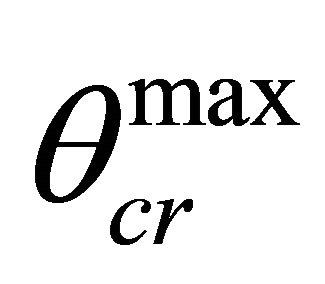 near the space with speed c, to
near the space with speed c, to 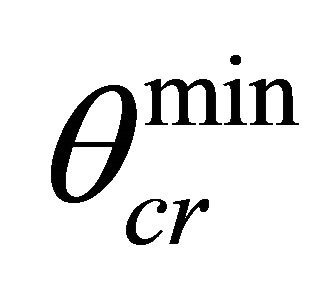 near space with speed c1 where
near space with speed c1 where . It means that to the boundary with
. It means that to the boundary with 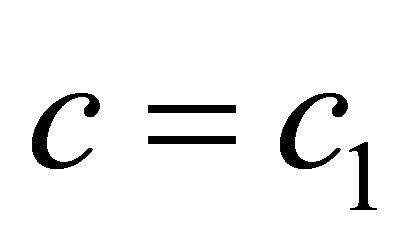 will come rays with
will come rays with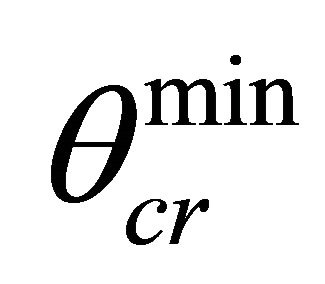 . Rays with
. Rays with 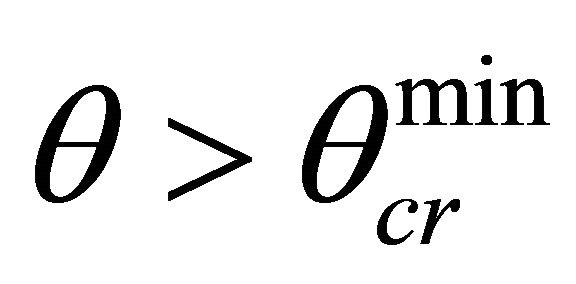 will turn nearer to space where speed’ sound equal c. Thus at every point of Δz come rays with
will turn nearer to space where speed’ sound equal c. Thus at every point of Δz come rays with ,
,  is a real value always. The additional phase in point of FIR about which it is spoken in [4], is connected with wrong record in (7) phase of the reflected wave. At a writing of the reflected wave in the form (8) the additional phase in a point of FIR is not present. Briefly these results bring in [13].
is a real value always. The additional phase in point of FIR about which it is spoken in [4], is connected with wrong record in (7) phase of the reflected wave. At a writing of the reflected wave in the form (8) the additional phase in a point of FIR is not present. Briefly these results bring in [13].
Let’s pass to an alternative way of calculation CR and CP sound waves. In it the condition of equality of phases of all three waves on the boundary also is used. Therefore after an exception of phases of boundary conditions it is possible to consider each wave as a vector. Calculation CR and CP is under construction on connection of three vector. The sum of squares of vectors of anew arisen waves is by means of preliminary summation of their projections to axes of co-ordinates. We consider, as well as above, that the amplitude of a falling wave is equal 1, reflected V1, passed W1. We will receive two equations for definition V1, W1, using a rule of addition of vectors through their projections to axes of co-ordinates, Figure 1:
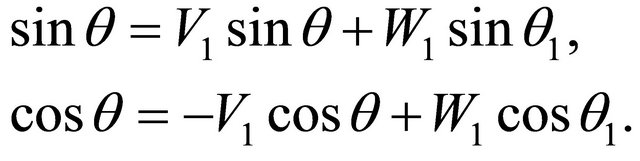 (11)
(11)
In Equation (11) the account of density of spaces is not spent since in the course of calculations they in final formulas do not get. The first equation in (11) is a projection of amplitude of a vector of a falling wave to an axis x, expressed through the sum of projections of amplitudes of vectors of the reflected and passed waves, the second— the same for projections of amplitudes of waves to an axis z. From 1st Equation in (11) and Snell’s law follows: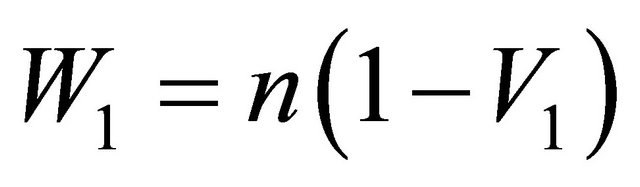 . Putting the Equation (11) in a square and summing them, we will receive, [13]:
. Putting the Equation (11) in a square and summing them, we will receive, [13]:
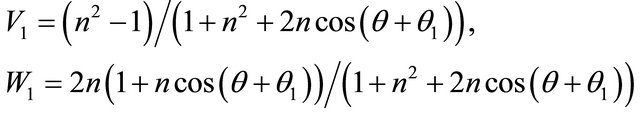 (12)
(12)
From Equation (12) it is seen that  when
when  for all angles of departure. Consider expressions (12) when
for all angles of departure. Consider expressions (12) when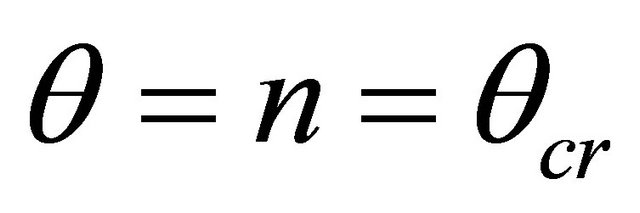 , an angle of FIR for CR V in Equation (10), and
, an angle of FIR for CR V in Equation (10), and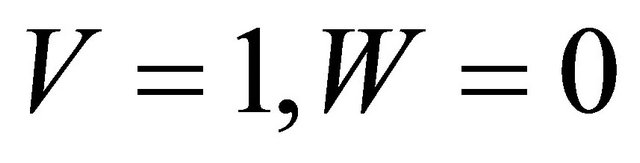 , passage wave absent. It is easy to show that from equations (12) it is followed that when
, passage wave absent. It is easy to show that from equations (12) it is followed that when  and passed wave absent,
and passed wave absent, . Thus in vector’s method of calculation CP and CR there is exist the full inner reflection of sound waves too when
. Thus in vector’s method of calculation CP and CR there is exist the full inner reflection of sound waves too when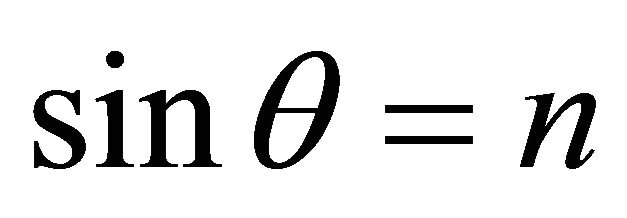 .
.
For comparison of two methods of reception CR and CP we will carry out their calculation along a trajectory of a sound wave in a wave-guide of canonical type. In [3] it is shown, that geometrical acoustics in such wave-guides is applicable. This type of a wave-guide is interesting to that on it’s parameters which is close to real oceanic waveguides in separate areas of the world ocean.
Let’s accept, that depth of a wave-guide of 4 km, a sound source is placed on a wave-guide axis on depth  where speed of a sound is minimum. We will choose the most abrupt trajectory, not concerning a surface and a bottom, with an angle of departure towards a bottom
where speed of a sound is minimum. We will choose the most abrupt trajectory, not concerning a surface and a bottom, with an angle of departure towards a bottom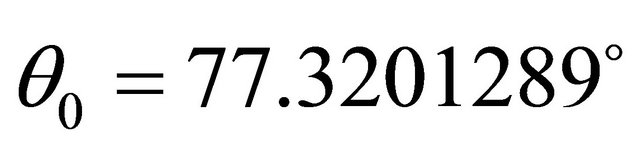 . The turning point at a bottom lays on depth
. The turning point at a bottom lays on depth . We will break a waveguide on depth into layers in width
. We will break a waveguide on depth into layers in width , refracttion’s coefficient on the boundary of layers
, refracttion’s coefficient on the boundary of layers 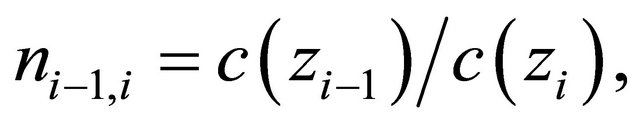
 —speed of a sound in a point zi, i—layer number. Values θ0, θ’, z’ correspond to a trajectory, which turning point is below a surface on an interval δz. By calculation the chosen trajectory the angle FIR (turning point), equal to
—speed of a sound in a point zi, i—layer number. Values θ0, θ’, z’ correspond to a trajectory, which turning point is below a surface on an interval δz. By calculation the chosen trajectory the angle FIR (turning point), equal to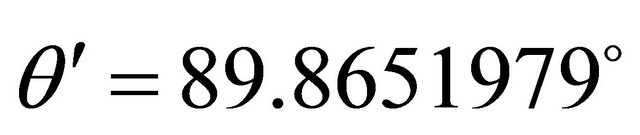 . On Figure 2 coefficients V, W and V1, W1, calculated along a trajectory of a sound wave are showed as functions of an angle along trajectory θ, horizontal axis. Angle θ may be considered as an angle of departure from the source. Coefficients V, W calculated when m = 1. The bottom curves show dependence CR V, V1 from θ. Practically in all angular range V and V1 are close to zero. At an exit from a source
. On Figure 2 coefficients V, W and V1, W1, calculated along a trajectory of a sound wave are showed as functions of an angle along trajectory θ, horizontal axis. Angle θ may be considered as an angle of departure from the source. Coefficients V, W calculated when m = 1. The bottom curves show dependence CR V, V1 from θ. Practically in all angular range V and V1 are close to zero. At an exit from a source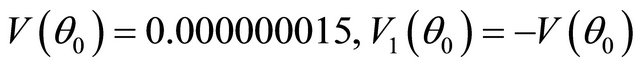 . Nonzero values CR accept near to a point of FIR at a bottom. In a turning point (FIR) at
. Nonzero values CR accept near to a point of FIR at a bottom. In a turning point (FIR) at  Coefficients of passage W, W1, the top curves on Figure 2, coincide,
Coefficients of passage W, W1, the top curves on Figure 2, coincide, 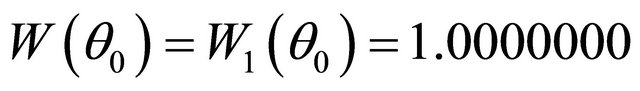 , up to corners θ ~ 89.81˚, where
, up to corners θ ~ 89.81˚, where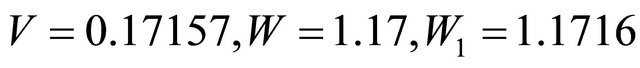 . At
. At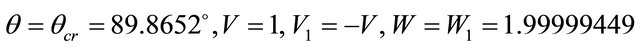 . From the showed data it is visible, that the ray’s turning point θ’ coincides with an angle of FIR for two ways of calculation. With removal from a point of FIR modules of coefficients of reflection V and V1 decrease, and coefficients W, W1 grow. Thus, at decrease z (and θ) dependences V, W and V1, W1 from θ are mirror symmetric resulted on Figure 2. Calculations show, that along all trajectory, except for area near to FIR points, sound energy is transferred by the passed wave. To vicinities of points of FIR sound energy is transferred both passed and the reflected wave, in the FIR point– by the reflected wave only. On Figure 3 the result of calculation CR and CP along all cycle of a trajectory, and also a trajectory as functions of a horizontal distance x (horizontal axis) from a source is showed. The part of vertical axis is the depth of waveguide from the surface, point z=0, to bottom, point z = 4 km. The values of V, W, V1, W1 are showed at vertical axis from point –1.1 to point 2.3. As well as on Figure 2, V and V1, calculated by two methods, are practically equal to zero, between points of FIR. In these points CR increase to values, on the module equal 1. CP change as follows: between turning points W = W1 =1, in FIR points
. From the showed data it is visible, that the ray’s turning point θ’ coincides with an angle of FIR for two ways of calculation. With removal from a point of FIR modules of coefficients of reflection V and V1 decrease, and coefficients W, W1 grow. Thus, at decrease z (and θ) dependences V, W and V1, W1 from θ are mirror symmetric resulted on Figure 2. Calculations show, that along all trajectory, except for area near to FIR points, sound energy is transferred by the passed wave. To vicinities of points of FIR sound energy is transferred both passed and the reflected wave, in the FIR point– by the reflected wave only. On Figure 3 the result of calculation CR and CP along all cycle of a trajectory, and also a trajectory as functions of a horizontal distance x (horizontal axis) from a source is showed. The part of vertical axis is the depth of waveguide from the surface, point z=0, to bottom, point z = 4 km. The values of V, W, V1, W1 are showed at vertical axis from point –1.1 to point 2.3. As well as on Figure 2, V and V1, calculated by two methods, are practically equal to zero, between points of FIR. In these points CR increase to values, on the module equal 1. CP change as follows: between turning points W = W1 =1, in FIR points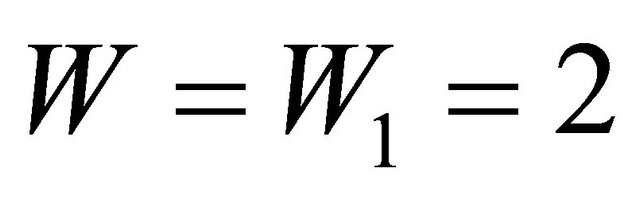 .
.
Comparison of length of trajectory R and lengths of cycle D with trajectory calculation when it was accepted, that in turning points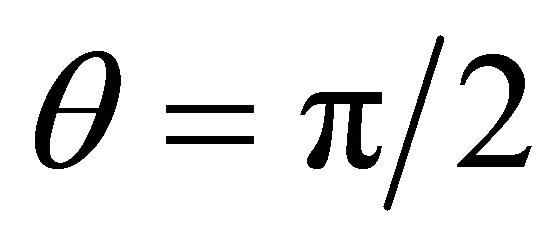 , shows, that for a trajectory on Figure 3 length R has decreased on 1.30131 km, and length D for 1.11211 km.
, shows, that for a trajectory on Figure 3 length R has decreased on 1.30131 km, and length D for 1.11211 km.
4. Conclusions
Let’s note the following results for the consideration.
It is shown that in a number of works there is an error in calculation of a spatial part of phase of a running sound wave. Its essence consists that independence of scalar

Figure 2. Coefficients of reflection and passage as functions at angle of departure from the source.
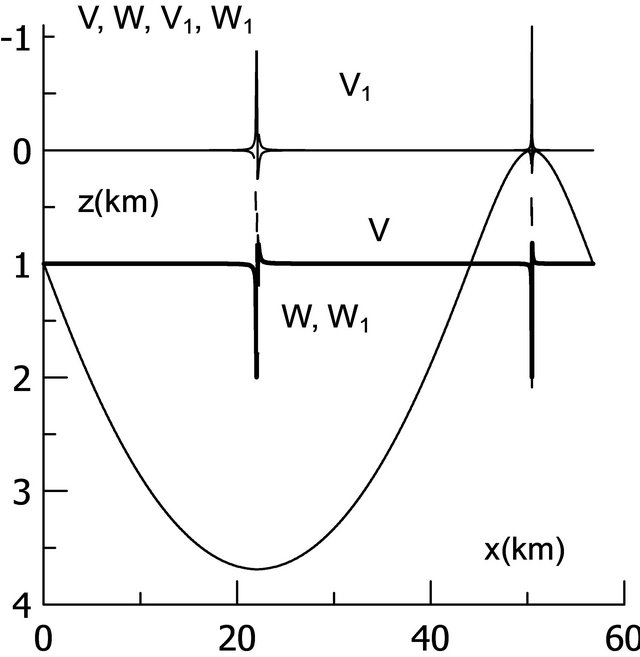
Figure 3. Ray trajectory and coefficients of reflection and passage along trajectory as functions of distance x.
product of a wave vector and a vector along a trajectory from system of co-ordinates in which both vectors are presented are not taken into consideration. One of conesquences of this error is possible reduction of calculated distance (propagation time), passed by a wave in the nonuniform space.
The decision of the wave equation with reference to propagation of plane sound waves is considered. It is shown that with correct treatment of scalar product, one of decisions of the wave equation under certain conditions can be considered as propagation of a plane wave to any direction from a source, while other decisions do not satisfy the equations of oscillatory movement of a liquid.
As a result of correction of error at record of a spatial part of a phase it is received, existing formulas for coefficients of reflection and passage are applicable on any depth of boundary of two spaces.
It is shown that a turning point of trajectories in a wave-guide is the point of full internal reflection of a sound wave. It means that the tangent to a trajectory in this point is not horizontal. Reflection’s coefficient in a point of full internal reflection is the real value at any angles of departure sound waves from a source. All energy of a sound wave in points of full internal reflection is concentrated in the reflected wave.
Coincidence turning points of a trajectory in a waveguide with a point of full internal reflection leads to reduction of an angular range of a ray along a trajectory (an angle of full internal reflection less ) and accordingly to reduction of length of a cycle and a trajectory throughout one cycle.
) and accordingly to reduction of length of a cycle and a trajectory throughout one cycle.
The vector way of calculation of coefficients of reflection and passage in which the amplitude of each wave is considered as a vector coinciding with a direction of its propagation is offered. Calculation of coefficients of reflection and passage by vector and traditional ways yield to practically conterminous.
REFERENCES
- V. A. Zverev, V. P. Ivanov and G. K Ivanova, “Calculation of the Sound Field in the Oocean in Caustic Surfaces by the Ray Method,” Proceedings of the 22th Conference of the Russian Acoustic Society, Moscow, 2010, pp. 191- 193.
- V. A. Zverev, V. P. Ivanov and G. K. Ivanov, “Reports of 13th a School—Seminar Акад. L.M. Brehovskikh, Caustics in the Underwater Channel and Their Connection with the Wave’s Front of Point Source,” ГЕОС, Moscow, 2011, pp. 49-52.
- “Caustics in the Underwater Channel and Their Connection with the Wave’s Front of Point Source”. www.iapras.ru/publication/preprint/ca11.pdf/
- L. M. Breovskikh, “Waves in Layered Environments,” The Science, 1973.
- L. D. Landau and V. M. Lifshits, “Hydrodynamics,” The Science, 1988.
- L. M. Brehovskikh and O. A. Godin, “Acoustics of NonUniform Environments,” The Science, 2007.
- L. M. Brehovskikh and A. A. Goncharov, “Introduction in Mechanics of Continuous Environments,” The Science, 1982.
- I. Smirnov, “A Higher Mathematics Course,” The State Publishing House Physics-Mathematical Literature, 1958.
- Н. E. Кочин, “Vector Calculation and the Beginnings Tensor Calculations,” The Science, 1965.
- I. E. Tamm, “Bases of the Theory of an Electricity,” Science, 1966.
- G. S. Landsberg, “Optics,” The State Publishing House of the Technique-Theoretical Literature, 1940.
- I. Tolstoy and K. S. Klej, “Acoustics of Ocean,” The World, 1969.
- G. K. Ivanova, “One Aspect of Sound Waves Propagation in Inhomogeneous Water Space,” Proceedings of the 25th conference of the Russian Acoustic Society, Moscow, 2012, pp. 338-341.

