World Journal of Engineering and Technology
Vol.05 No.03(2017), Article ID:77560,18 pages
10.4236/wjet.2017.53030
Fundamental Laws of Physics and Calculation of Heat Transfer in Combustion Chambers of Gas-Turbine Plants
Anatoly Nikolaevich Makarov
Department of Electrical Supply and Electrical Engineering, Tver State Technical University, Tver, Russia

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 7, 2017; Accepted: July 9, 2017; Published: July 12, 2017
ABSTRACT
The laws of heat radiation from black body, the laws of Stefan-Boltzmann, Planck, and Wien are fundamental laws of physics. All in all, a little more than 30 fundamental laws of physics, studied by pupils and students worldwide were disclosed. Scientific disclosure of fundamental laws influences mainly power technology, fuel and energy resources saving. In the late XIX century the laws of heat radiation from gas volumes and the laws of Makarov were disclosed. Since the radiation laws from blackbody are fundamental laws of physics, then the laws of heat radiation from gas volumes are fundamental laws of physics. Effect of using laws of heat radiation from gas volumes on fuel saving, reduction of development pressure on the environment in many countries of the world is shown. Calculation results from heat transfer in combustion chamber of gas-turbine plant are described. The torch in a combustion chamber is modeled by cylindrical gas volumes. Fluxes data from the torch and convective fluxes of cooling air are confirmed by measuring data from chamber-wall temperature.
Keywords:
Physics, Scientific Discovery, Laws, Nobel Prize, Heat Radiation, Gas Volumes, Combustion Chamber

1. Introduction
The XIX century is characterized by the creation and wide use of steam engines in industry, rail and water transport. Steam engine is a heat piston engine in which steam energy becomes work to be done. Steam engines laid the foundation for humanity transition from agricultural to industrial production.
The construction and mass creation of steam engines became possible after the discovery of the fundamental laws of physics concerning the relationship between the parameters of steam and gas. R.Boyle in 1662 discovered the relationship between pressure of gases (Boyle-Mariotte law) [1] .
J.L. Gay-Lussac in 1802-08 discovered the laws of heat expansion of gases and volumetric ratios during reactions between gases (Gay-Lussac laws).
D. Dalton in 1801-08 years disclosed the laws of partial pressures of gases [2] . A. Avogadro in 1809-1919 disclosed a gas law concerning the relationship between the number of molecules, volume, pressure and temperature of gases (Avogadro’s Law).
B. Klaiperon and D.I. Mendeleev derived the equation of state of an ideal gas. (the Klaiperon-Mendeleev equation, 1874) [3] . The efficiency of the first steam engines, created in 1780-90s, was 0.3% - 0.4%. The discovery of the laws of molecular physics and thermodynamics made it possible to calculate steam parameters and design steam engines, increasing their efficiency, reducing fuel consumption. In the late XIX the efficiency of steam engines was increased 60 times from 0.3% - 0.4% to 20%.
Steam engines were used as stationary engines of machine tools and equipment for use in factories, plants, boats.
Until the late XIX century, steam engine was practically the only common engine in industry and transport. Due to the low efficiency of steam engines and the massive construction of electric power stations at the beginning of the twentieth century, steam engines at power plants were replaced by steam turbines, whose efficiency currently accounts for 86% - 88%.
2. Fundamental Laws of Physics
2.1. Laws of Radiation from Black Body
Steam-engine vapor, steam turbine vapor are obtained in steam boilers- installations for converting water into vapor through the heat, released in a furnace during fuel combustion.
In the XIX-early XX centuries solid fuel: coal, peat, slantsy, wood were fired on grates infurnaces. The energy released under combustion of fuel, consists of energy of heat radiation to the extent of 90% - 95%. Before 1879-84 solid fuels as a source of heat radiation was a “black box” an unexplored radiating solid body. The furnaces of steam boilers were created empirically, that excepted the possibility to calculate the heat transfer between the fuel and the heating surface, so the efficiency of furnaces was 20% - 25%.
The law of heat radiation from blackbody, solid body was formulated by Th. Stefan in 1879 by experiments, in 1884 by L. Boltzmann by theory. In 1893 Wien has found a relationship between wavelength and temperature of a blackbody (Wien displacement law) [4] [5] . In
 (1)
(1)
where q is the density of the net radiation flux of fuel to the heating surface F2; φ12 is the local angular emissivity of solid fuel surface of F1 area to the heating surface F2, that shows the portion of radiation F1 on F2 from all the radiation F1 in the surrounding space; T1, T2 is the temperature of the layer of fuel and the heating surface,, respectively; cs is the Stefan-Boltzmann constant; ε1 is the emissivity of fuel surface.
The disclosure of the laws of heat radiation from solid fuel, the laws of Stefan- Boltzmann, Planck, Wien allowed to create a geometrical, physical, mathematical model of solid fuel as a source of heat radiation and to develop an analytical method for calculation of heat transfer in furnaces and combustion chambers. With the disclosure of the laws solid fuel as a source of heat radiation becomes an investigated physical body, not a “black box”. Using the laws of heat radiation from blackbody, solids, researchers, designers carry out calculations of heat transfer in furnaces, improve steam boilers, that enhances the efficiency of steam boilers from 20% - 25% to 90% - 95%, that is 3 - 4 times, reduces 3 - 4 times the fuel consumption for generation of 1 kW×h of electricity in power stations, saves 1 million tons of fuel. V. Wien in 1911 and M. Planck in 1918 were awarded Nobel Prize in physics for the discovery of the laws of heat radiation from a blackbody. The laws of heat radiation from blackbody, solids are both fundamental laws of physics [1] [2] . Students of schools and universities all over the world study the fundamental laws of physics.
2.2. Basic Laws of Physics
Laws of physics form the basis for all natural science. It is known from school and university courses of physics, that a little more than 30 laws, named after their authors, underpin the whole of physics.
Basic fundamental laws of physics, which bear the surnames of scientists in chronological order, since antiquity till present are as follows. Archimedes’ principle (the 3rd century BC), Galilei laws (1590-1620), Kepler’s laws (1609-19), Huygens’ laws (1650-80), Hooke’s law (1660), Boyle’s laws (1662), Newton’s laws (1666-1704), Avogadro’s law (1809-19), Gay-Lussac’s laws (1802-09), Dalton law (1801-08), Ampere’s law (1820-25), Fourier’s law (1823), Ohm’s law (1826), Faraday laws (1831-34), Joule-Lenz’s law (1841-42), Kirchhoffs laws (1845-47), Maxwell equations (1860-73), Mendeleyev’s law (periodic law, 1869). At the end of the 19th, 20th centuries the following fundamental laws of physics, named after their authors, were disclosed. Stefan-Boltzmann law, the law of heat radiation from black body,1879-84; Joseph John Thomson developed the theory of charged-particle motion in an electromagnetic field, discovered the electron, 1897-1912., Nobel prize for physics in 1906; Becquerel discovered radioactive phenomenon in 1896, Nobel prize for physics in 1903; Wien’s law, displacement law of heat radiation from black body, 1893., Nobel prize for physics in 1911.; Planck law, the law of heat radiation from black body, 1900., Nobel prize for physics in 1918.; Rutherford proposed planetary atom model in 1911, Nobel prize for chemistry in 1908.; Einstein developed the theory of relativity, established photo effect phenomenon, 1905-15, Nobel prize for physics in 1921.; Bohr’s postulates, developed quantum theory of atom and radiation from it, Nobel prize for physics in 1922.
Fundamental laws of physics each are unique phenomena in the history of physics, natural history, humanity as contributed significantly to development of science and technology. Since the establishment of the Nobel Prize in 1901, all the scientists, which disclosed fundamental laws of physics, such as laws of heat radiation have been bestowed upon this award: Wien, Plank, Bohr.
In 20th century (between 1923 and 2015) the following discoveries and inventions, given in chronological order, were made and the authors of which got Nobel Prizes: Roentgen rays, color photo, radio, new alloys, neutron, positron, proton, meson, cosmic rays, semiconductors, transistors, Cherenkov effect, masers, lasers, superconductivity, superfluidity, neutron spectroscopy, semiconductor heterostructures, LEDs, optical data transmission systems, Universe expansion. Analysis of discoveries and inventions of 1923-2015, which authors were awarded the Nobel Prize, shows that none is a fundamental law of these profound inventions and discoveries which would be included texts on physics for secondary schools and engineering and technology occupations.
2.3. Numerical Methods for Calculating Physical Phenomenons
Lack of scientific discoveries of fundamental laws of physics in mid-end of the 20th century is obviously related to appearance of computers and use of numerical methods for calculating physical phenomenons and physical processes on computers. With the appearance of computers in 1940s, hundreds of numerically generated programs on computers for integrable equations, describing physical processes were created.
For example, universal software package: Sigma Flow allows to calculate the following physical phenomena and processes: laminar and turbulent flows, the processes of mixing and diffusion of gas mixtures, chemical reactions in the flow, combustion of gaseous, liquid, pulverized fuel, convective, radiant heat transfer, heat conduction, movement of particles in gas flow, drying, pyrolysis, combustion particles [6] . Numerical simulation was used in the analysis of design decision of boiler P-50P [7] .
In the modelling work, the following physical phenomena and processes were calculated: aerodynamics, combustion, heat transfer, formation of nitrogen oxides in the furnace on the basis of programs of Sigma Flow.
The program is the best solution to calculate fields of gas dynamics, burning, gas-sphere composition, temperature distribution and heating fluxes in furnaces.
However, the application of highly expensive and technically complex programs is not always necessary and justified.
A number of practical problems can be solved using relatively simple empirical and analytical methods.
The computer, dealing with a large number of data, can create an illusion of inclusiveness of the studied phenomena and processes. However, the computer also contributes to the reproduction of details and particulars of the studied phenomenon, giving an important role to private cases. Numerical methods for calculating physical phenomena and physical processes on computers do not stimulate the analytical solution of differential and integral equations, derivation of formulas, the discovery of the laws of physical phenomena. Scientists enjoy the illusion that they do not need solving the integral equations, deriving the formulas, discovering the laws, that describe the behaviour of physical phenomena and processes, it is sufficient to solve integral equations numerically on the computer.
However, the derivation of the formulas, the discovery of the laws, describing physical phenomena and development of numerical together with analytical calculation methods is very important. The information overwhelmed by the great amount of details obscuring the essence of the processes need to be compressed, turned into a small number of laws, concepts. An analytical method that uses the laws, formulas, does not require sophisticated software and computers with large memory capacity, the problem can be solved by the designer and the student on a personal computer. Therefore, the discovery of the laws of physical phenomena, the derivation of the formulas for the development of analytical methods for calculating physical phenomena is very important for science and technological development.
3. Laws of Radiation from Gas Volumes
3.1. Calculation Problem for Radiation from Gas Volumes
In XX-XXI centuries flaring of gas, liquid, pulverized fuel in furnaces, fire boxes, combustion chambers was widespread. Fuel flaring is characterized by volume emission, a three-dimensional radiation model [4] [5] [8] [9] . In torch, gas volume, emit 1015 - 1030 particles, atoms. Radiation of each particle, atom on the calculated area should be considered. The calculation of heat radiation on the calculated area of all the atoms in the gas volume, the torch requires the solution of triple integral equations [9] . The solution of triple integral equations to determine the average path length of beams from the emitting particles, atoms, angular radiation coefficients of the gas volume on the calculated area in the XX-XXI centuries was not bee found [9] [10] . The laws of radiation from gas volumes were not disclosed.
It is considered, that the problem of calculating heat transfer in torch furnaces, fire boxes, combustion chambers was solved with the appearance of computers and the use of numerical simulations of integral equations of heat transfer [4] [5] [6] [7] [8] . However, long-term analytical and experimental studies of heat transfer have shown that the results of the numerical solution of integral equations of heat transfer on computers are not valid [11] . The method uses the laws of heat radiation of a blackbody, solid bodies, Stefan-Boltzmann law (1), however, gas volume radiation is not subject to the laws of Stefan-Boltzmann [11] . This method uses the Stefan-Boltzmann law and a large mass of approximate values of the temperatures and optic coefficients of surface and volume zones, and the accuracy of calculations is 20% - 40% [11] [12] .
In the XX century, the torches, emitting gas volumes remained a “black box” despite the applied enormous intellectual resources to solve the problem. Formulas for determination the main parameters of heat radiation from gas volumes, torches, formulas for determination average beam path length from quadrillions of radiating atoms, the local angular coefficients of radiation from radiation flux densities on the calculated area were not available. The solution to the problem has stalled.
3.2. Laws of Radiation from Spherical and Cylinder Gas Volumes
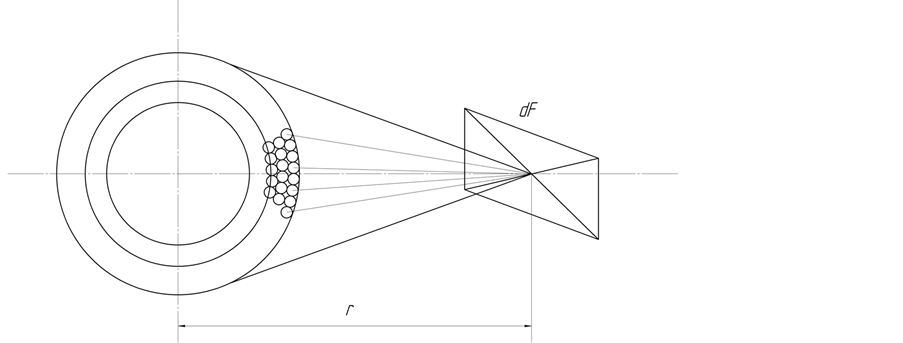
At the end of the 20th century, in 1996-2001 the laws of heat radiation from gas volumes [13] [14] [15] , the laws of heat radiation from gas isothermal isochoric concentric spherical (Figure 1) and coaxial cylinder gas volumes (Figure 2) that
Figure 1. The radiation from isothermal isochoric concentric spherical gas volumes on the calculated area dF.
Figure 2. The radiation from isothermal isochoric coaxial gas volumes on the calculated area dF.
the torches, gas volumes of the furnaces, fire boxes, combustion chambers are modeled by at present [16] [17] [18] .
The laws are called Makarov’s laws with the goal of adherence to the age-old scientific traditions and copyright [13] . Based on the scientific discovery geometric, physical, mathematical models of gas volume, torch as a source of heat radiation has been developed. Spherical or cylindrical gas volumes inscribe in gas volumes formed during fuel flaring. Radiating gas atoms are simulated by emitting quadrillions of spheres, uniformly filling the spherical and cylindrical gas volumes.
The statement of the scientific disclosure is as follows. “The average path length of beams from quadrillions of radiating particles of each isochoric isothermal concentric spherical or coaxial cylindrical gas volumes to the calculated area is equal to the arithmetic mean distance from the symmetry axis of volumes to the calculated area and the angular coefficients, flux densities of radiation from gas volumes on the calculated area are equal. The flux density of radiation from the central spherical or central cylindrical gas volume of a small diameter on the calculated area is equal to the sum of the fluxes of the radiation fluxes from all the concentric spherical or coaxial cylindrical volumes on the calculated area at the radiation power released in the volume of a small diameter, equal to the sum of the radiated powers released in all spherical or coaxial cylindrical gas volumes radiating on the calculated area.”
Mathematical notation of the laws is as follows:
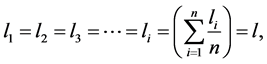 (2)
(2)
where  is the average beam path length from the first to the i-th cylindrical or spherical gas volumes to the calculated area dF; l is the the arithmetic mean distance from the axis of symmetry of the cylindrical volumes or the center of symmetry of the spherical volumes to the calculated area dF.
is the average beam path length from the first to the i-th cylindrical or spherical gas volumes to the calculated area dF; l is the the arithmetic mean distance from the axis of symmetry of the cylindrical volumes or the center of symmetry of the spherical volumes to the calculated area dF.
 (3)
(3)
where 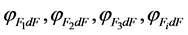 is the local angular coefficient of radiation from a surface of the first, second, third, the i-th coaxial cylindrical or concentric spherical gas volumes on the calculated area dF, respectively.
is the local angular coefficient of radiation from a surface of the first, second, third, the i-th coaxial cylindrical or concentric spherical gas volumes on the calculated area dF, respectively.
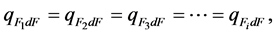 (4)
(4)
where 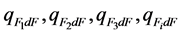 is the density of the radiation fluxes incident from the first to the i-th coaxial cylindrical or concentric spherical gas volumes on the platform dF.
is the density of the radiation fluxes incident from the first to the i-th coaxial cylindrical or concentric spherical gas volumes on the platform dF.
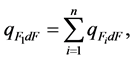 (5)
(5)
where 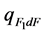 is the density of radiation flux incident from the central cylindrical or spherical gas volumes of a small diameter on the calculated area dF.
is the density of radiation flux incident from the central cylindrical or spherical gas volumes of a small diameter on the calculated area dF.
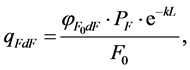 (6)
(6)
where  is a local angular coefficient of radiation from the central cylindrical or spherical gas volumes of a small diameter on the calculated area dF; PF is the radiation power of the central cylindrical or spherical gas volumes; F0 is is the area of the calculated platform dF.
is a local angular coefficient of radiation from the central cylindrical or spherical gas volumes of a small diameter on the calculated area dF; PF is the radiation power of the central cylindrical or spherical gas volumes; F0 is is the area of the calculated platform dF.
Mathematic notation of the laws of heat radiation from gas volumes, the laws of Makarov is obvious and grounded in a similar manner to the statement and mathematic notation of Newton’s Third Law of Motion in texts on physics for students of secondary schools and technical universities:
“The force with which two bodies act upon each other are equal in magnitude and opposite in direction.”
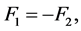 (7)
(7)
where F1 is the force with which the body 1 acts on body 2; F2 is the force with which the body 2 acts on body 1.
Laws of heat radiation from gas volumes possess the compactness, the accuracy of the description of physical phenomena in a similar manner to the fundamental laws of physics. For example, a fundamental law of physics, Ohm’s law describes the relationship between the current I flowing in the conductor, the voltage U applied to the conductor, and the conductor resistance R:
For example, a fundamental law of physics, Ohm’s law describes the relationship between the current I flowing in the conductor of the voltage U, applied to the conductor, and the conductor resistance R:
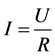 (8)
(8)
Similarly, the law of heat radiation from gas volumes characterizes the dependence of flux density of heat radiation q of gas volume from the angular coefficient of the radiation φ, radiated power P, the average beam path length rays l of gas volume. For calculation of parameters of heat radiation from gas volumes (6) φ, P, l analytical expressions, formulas were derived [18] .
A unique, natural harmony of heat radiation from quadrillions of particles of spherical and cylindrical gas volumes is disclosed, namely, that the average beam path length from these particles is equal to the arithmetic mean distance from the symmetry axis of volumes to the calculated area.
Complex, a triple integration of no solution within the gas volume to determine the average beam path length is reasonably replaced by computing actions of elementary mathematics, analytic geometry, this produces the same result, which would have been got in triple integration.
The uniqueness of the scientific discovery is that the flux densities of radiation, angular radiation coefficients of spherical, coaxial, cylindrical gas volumes to the calculated area are equal and it is sufficient to hold a single integration of trigonometric functions within the height of the cylindrical gas volume of a small diameter, located on the axis of symmetry to define them [10] [18] [19] [20] [21] .
Heat radiation from cylindrical gas volumes of diameter 2, 5,
With the discovery and development of the laws of geometrical, physical and mathematical models of torch, the radiating gas volumes, torches as sources of heat radiation become an investigated physical phenomenon, not a “black box”. The formulas for calculating the density of the radiation flux of the gas volume of the torch on the calculated area (6), to determine the local angular coefficient of the gas volume on the calculated area [10] [18] [19] [20] [21] , to determine the average path length of the rays quadrillion (2) from the gas volume to the estimated vehicle [9] . Based on the scientific discoveries of the laws of thermal radiation of the gas volume developed the theory of thermal radiation of the gas volume and the new concept of calculating heat transfer in torch furnaces, fire chambers, combustion chambers [18] . The theory of thermal radiation of the gas volume includes the output 14 of the formulas for calculating the coefficients and fluxes of the radiation of the flame on the heating surface in vivarelli, mutually perpendicular coils and arbitrarily located planes.
3.3. A New Concept for Calculating Gas Volume Radiation
In accordance with the new concept and the theory cylinder gas volumes, from which the calculation of radiation fluxes on the calculated areas and heating surfaces is performed, are inscribed in torches.
Radiation fluxes from torch, heated surfaces, combustion products is determined for each calculated area taking into account multiple reflections and Torch i For each calculated area platform determined by taking into account multiple reflections and absorptions. The calculations of heat transfer in steam boiler boxes [11] [12] [17] [18] [19] , torch heating furnaces [9] [10] [14] [15] [16] , combustion chambers of gas turbine installations [18] are made with the use of the new concept.
The calculations allow to determine rational energy modes of electric arc and torch furnaces, fire boxes, combustion chambers in which fuel consumption reduces, operational life increases. In fifteen years since the first publication of the author of scientific discovery in printing, theory of thermal radiation of the gas volume and the new concept of calculating heat transfer in torch furnaces, fire chambers, combustion chambers have been tested by time, the results of calculations are confirmed by results of experimental studies on existing kilns, furnaces, combustion chambers, the accuracy of calculations does not exceed 10%. Since the radiation laws a blackbody, the laws of Stefan-Boltzmann, Planck, these Wines belong to the fundamental laws of physics, and the laws of radiation by gas volumes are both fundamental laws of physics.
Laws of heat radiation, theory of heat radiation from gas volumes and the new concept of calculation in electric arc and torch furnaces, fire boxes, combustion chambers were published in the form of text [18] , which is used for teaching university students. The method for calculation that had existed until the scientific discovery had not allow to calculate and to manage rational heat transfer in torch furnaces, since the error of calculations was 20% - 50%, so the efficiency of fuel energy in torch furnaces is 25% - 45% at the present time. The use of scientific discovery and its base-developed theory allows to determine the rational parameters of the torch (capacity, length, expansion angle) and its spatial position to the heating surface (vertical, horizontal, inclined at a certain angle).
Rational position of products and torches, burners will increase consumption efficiency of fuel energy half-two fold from 25% - 45% to 65% - 75%, decrease fuel consumption twofold over the coming years all over the world.
We shall now complement the example of calculating heat transfer in torch furnaces [9] [10] [14] [15] [16] , steam boiler boxes [11] [12] [17] [18] [19] [20] [21] , electric arc steel melting furnaces [18] with an example of calculating heat transfer in gas turbine combuster.
4. Example of Calculation of Heat Transfer in the Combustion Chamber by the Laws of the Radiation from Gaseous Volumes, Laws of Makarov
4.1. The Device and the Method of Calculation of Heat Transfer in the Combustion Chamber
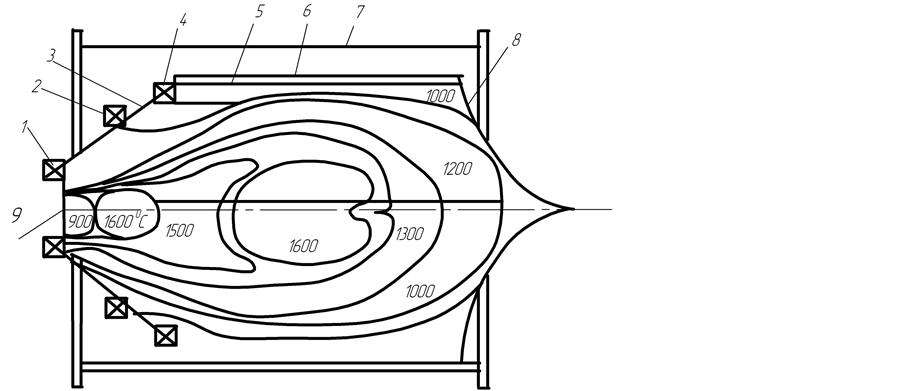
We will carry out the calculation of heat transfer in the combustion chamber of gas turbine unit (GTU) based on the laws of radiation from gas volumes. In order for an experienced designer and student of the technical University to repeat the calculations, we will consider the calculation of heat transfer in the combustion chamber with the torch of a simple structure and turbine-inlet temperature of 1000˚С. We use GTU GT-700-5M as the example for calculation. This unit had been used as a drive for gas transportation on gas pipelines since 1970s and its operation includes the data used in the calculations. Figure 3 shows a
Figure 3. Scheme of the combustion chamber and the distribution of isotherms over the torch volume: 1 and 2 are the first and second swirlers; 3 is a chamber pan; 4 is the outer swirler; 5 is the fire tube; 6 is the screen; 7 is the housing; 8 is the mixer; 9 is the burner.
diagram of the combustion chamber of the gas turbine GT-700-5M and the location of isotherms over the volume of the torch.
The gas temperature before the turbine is 1000˚C.Consumption and fuel specific energy (natural gas), 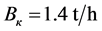 , respectively;
, respectively;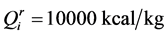 , GTU efficiency at the rated power is 32%, excess primary air factor is 2.4, power 5,2 MW.
, GTU efficiency at the rated power is 32%, excess primary air factor is 2.4, power 5,2 MW.
The field of tangential velocity changes from 70 m/s at swirl up to 60 m/s in the center of the chamber and 45 m/s at the mixer. The air temperature increases from 360˚C at the swirler to 400˚C in the center of the chamber and 450˚C at the mixer. The local temperature of combustion liner wall changes from 500˚C at the swirler to 550˚C in the center of the chamber and 500˚C at the mixer.
The length of the combustion chamber is
Heat flux, or capacity released in torch during the combustion of fuel, we determine by the expression

Form a proportion to calculate the power distribution in volume zones of a torch:
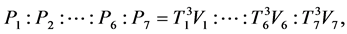
where Р1 − Р7 are the powers, released in volume zones of the torch, cylinder; Т1 − Т7, V1 − V7 are the temperatures and volumes of zones, cylinders.
Using the expression (10), we determine the powers, released in volume zones of the torch, cylinders, which the torch is modeled by: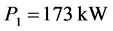


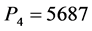
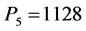
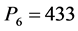

Calculate the densities of the total integrated heat fluxes incident on the i-th areas (they are seven by the number of elementary volumes) located on the surface of the combustion chamber, from the torch, heated surfaces, convective fluxes of torch [16] :
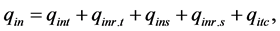
where 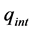





where 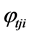
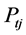



where 


where 

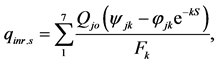
where 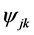

The net flux of the i-th area, causing its heating, is determined as the difference between the total integral heat flux incident on the area and effective heat flux, characterizing the total radiation flux from the i-th area:

where 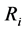



4.2. The Results of Calculation of Heat Transfer in Combustion Chamber
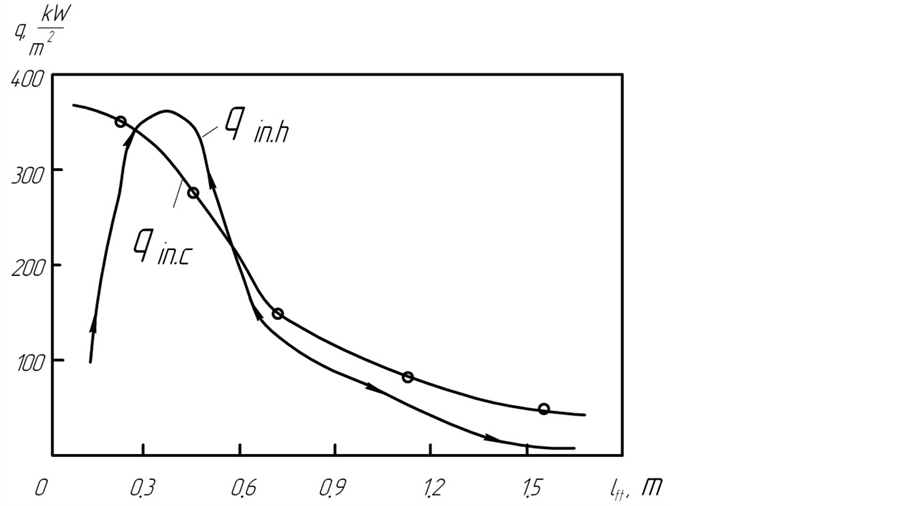
Figure 4 shows the graph of the distribution of the net flux, causing the heating of combustion chamber surface along the length of the flame tube.
Decisive influence on the density of the net flow has a density of the integral radiation flux from the torch: it is 95% of the density of net flux, calculated by the expressions (11) and (17).
The net flux density of heat is from 30 to 220 kW/m2 on the surface of small cone, from 220 to 350 kW/m2 on the surface of large cone.
The maximum density of the net flows of heating in the small cylinder reaches 360 kW/m2 in view of the fact that it is located in the zone the most close to the second-fourth volume zones of the torch, which release maximum powers.
The net heat flux densities reduce from 120 kW/m2 at the start of a zone to 70 kW/m2 at the end of zone in the fourth surface zone. This is because the fourth zone is shielded by a small cylinder from the radiation of the first, second and
Figure 4. Graphs of the distribution of heat and cool flux densities along the length of the flame pipe.
partially third volume zones of the torch. The net heat flux densities continue to decline in the fifth-seventh surface zones, from 70 kW/m2 at the start of the fifth zone to 8 kW/m2 at the end of the seventh surface zones, a continuing decline in the densities of the resulting flows with heating 70 kW/m2 in the beginning of the fifth zone to 8 kW/m2 at the end of the seventh. This reduction in the densities of the net flow of heating is associated with significant destruction of the fifth-seventh surface areas from the first-fourth volume zones of the torch, which release 89% of its capacity.
The result of heat transfer (heating and cooling of combustion chamber walls) depends on the difference between the net flux, causing heating of the walls, and the net flux, cooling walls, which is determined by the expression
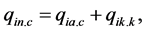
where 
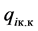
Summands in the expression (18) are calculated by he formulas:
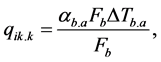

where 


The heat convection coefficient from the flame tube to the cooling air was calculated by the method described in [18] :

where 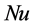



Reynolds Number was determined by the formula
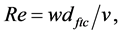
where w and v is the velocity and kinematic viscosity of the cooling air.
Figure 4 shows the results of calculation of the net flux, cooling the combustion chamber walls.
The walls of the bowl are cooled by the air both inside and outside, maximum density of convective cooling air is 350 kW/m2. The surface of the large cylinder of the flame tube is cooled primarily by the internal surface, the density of convective cooling air is 180 kW/m2 at the swirler. As the distance from the outer swirler decreases, the speed of the cooling air reduces with increasing air temperature, that affects the decrease in the density of the convective cooling air, which is 85 kW/m2 at the surface of the central zone of the large cylinder. Inner surface of the cylinder at the end of the flame tube is cooled by convective flow, density of 45 kW/m2.
Inner surface of the cylinder at the end of the flame tube is cooled by convective flow, its density is 45 kW/m2.
The results of the calculations show, that large cone of bowl operates in severe conditions, here the density of the net fluxes from the torch, causing the heating, exceeds the density of convective cooling air.
In the most favorable conditions there is a large flaming cylinder tube: convective removal of heat the cooling air exceeds the quantity of heat received by the surface of the cylinder from the torch. Under the best possible conditions runs the big cylinder of a fire tube: convective heat removal with cooling air exceeds the amount of heat, which the surface of cylinder receives from the torch.
As in the steady-state conditions state fire tube runs under isothermal conditions, we can assume that the excess heat from the bowl is transferred by heat conductivity to a large cylinder of the fire tube and is discharged by convective cooling air. This assumption is supported by the results of calculations of the amount of heat perceived by the calculated surface areas and the amount of heat removed by convective air from the calculated areas; they are approximately equal:
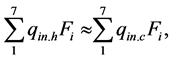
where 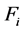
When performing equality (23), combustion chamber walls operate under isothermal mode. The calculated data of the distribution densities of the net flows from the torch and convection cooling air are in good agreement with the data of measurements of the local temperatures of the walls of the internal parts of the combustion chamber [18] : maximum temperature of the metal bowl corresponds to the maximum density of the net flows, causing heating of the surface of the bowl, and the minimum metal temperature at the end of the fire tube before the mixer corresponds to the minimum density of the net heat flux causing heating of the surface of the fire tube.
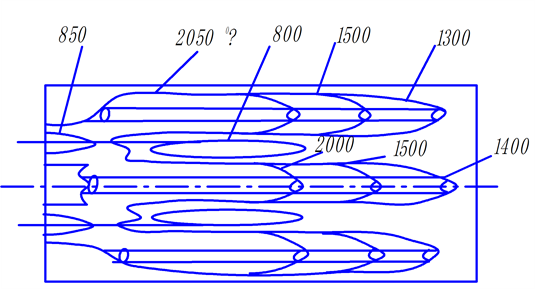
Similarly, we make the calculation of heat transfer in the combustion chamber with a more complex structure of the torch (Figure 5).
For example, in combustion chamber with seven burners, which generate seven “tongues” of the torch in the form of cones. In accordance with the above method and the distribution of isotherms on the torch, each cone is divided by 3 radiating cylinder gas volumes. The power in each cylinder is defined by the proportion (10) and the radiation flux density in the target point of the heating surface from 21 cylinders each and the total density of the integral radiation flux from the torch are determined by the expression (12). In the calculations the program complex of the “Kompas-3D”, “Microsoft Excel” was used.
5. Conclusions
Thus, in mathematical modeling of heat transfer, the torch in the combustion chamber of the gas turbine unit can be represented a volume body in the form of
Figure 5. The distribution of isotherms over the torch volume in the combustion chamber with seven burners.
radiating cylindrical gas volumes, which capacity and location depend on the distribution of isotherms in the combustion chamber. Power distribution by volume of the torch is characterized by significant irregularity.
Analysis of the net heat fluxes density distribution along the length of the combustion chamber showed their considerable unevenness: from 360 kW/m2 on the surface of a large cone up to 120 kW/m2 in the average combustion liner ring tube, and up to 8 kW/m2 in the last combustion liner annular zone by the mixer.
The distribution of the densities of the net convective cooling fluxes qualitatively corresponds to the schedule of densities distribution of the net fluxes of heating of surfaces of the combustion chamber: maximum density of cooling air of 350 kW/m2 is given from the surfaces of small and big cones of the bowl, then convective removal of heat reduces along the length of the combustion chamber, and the densities of the net convective cooling air in the central zone of the fire tube account for 85 kW/m2 and 45 kW/m2 in the last annular zone of fire tube by the mixer. When the surfaces of the combustion chamber operate in isothermal mode, the amount of heat supplied to its surfaces equals to the quantity of output heat by the convective cooling air.
The calculated data of the densities of the net heating fluxes and cooling of surfaces of the combustion chamber are in good agreement with the data of measuring the temperatures of the walls: the maximum heat flux density of heating obtained by calculations, corresponds to the maximum temperature of the bowl metal, and the minimum heat flux density of heating, obtained by calculation, corresponds to the minimum metal temperature at the end of the fire tube, obtained by calculations, which confirms the adequacy of the developed mathematical model to the real heat transfer processes occurring in the combustion chamber of a gas turbine unit.
The scientific discovery of the laws and the development of the theory of heat radiation from gas volumes is a contribution to the Foundation of modern physics, as it allows calculating and managing the transfer of heat around the world in tens of thousands electric arcs and torch furnaces, steam boiler boxes, combustion chambers of gas turbine units, reducing energy consumption and saving millions of tons of fuel, reducing emissions of pollutants and anthropogenic load on the environment, and improving the quality of life in many countries. The laws and the theory of heat radiation of the ionized and non-ionized gas volumes, the laws of Makarov were included in the text [18] , in the amount of fundamental knowledge on the quantum nature of radiation and are in line with the laws of heat radiation from absolutely black body, and with even more than thirty fundamental laws of physics.
Cite this paper
Makarov, A.N. (2017) Fundamental Laws of Physics and Calculation of Heat Transfer in Combustion Chambers of Gas-Turbine Plants. World Journal of Engineering and Technology, 5, 358-375. https://doi.org/10.4236/wjet.2017.53030
References
- 1. Timofeeva, T.I. (2001) Course of Physics. Vysshaya shkola, Moscow, 542 p. (In Russian)
- 2. Andreeva, О.N. (2006) Physics. Reference Book. Martin, Moscow, 272 p. (In Russian)
- 3. Akimov, M.L. and Logvinov, V.V. (2013) Dictionary of Modern Science. Librocom, Moscow, 248 p. (In Russian).
- 4. Siegel, R. and Howell, Y. (1975) Thermal Radiation Heat Transfer. Mir, Moscow, 934 р.
- 5. Blokh, A.G. and Zhuravlev, Yu.A. and Pyzhkov, L.N. (1991) Radiant Heat Transfer: A Handbook. Energoatomizdat, Moscow, 432 р. (In Russian)
- 6. Alekseenko, S.V., Burdukov, А.P., Dekterev, А.А., Markovich, D.М. and Shtork, S.I. (2011) Physical and Mathematical Modeling of Aerodynamics and Combustion in the Combustion Chamber of the Power Plant. Teploenergetika, 9, 67-72.
- 7. Maydannyk, М.N., Verbovetsky, E.H., Dekterev, А.А. and Chernetsky, М.Yu. (2011) Mathematical Modeling of Fire Box and Rotary Flue of Furnace P-50 R in Joint Combustion of Solid and Gaseous Fuels. Teploenergetika, 6, 37-42.
- 8. Oziric, M.N. (1976) Radiative Transfer and Interactions with Conduction and Convection. Mir, Moscow, 616 р. (In Russian)
- 9. Makarov, A.N. (2016) Modeling of a Torch and Calculation of Heat Transfer in Furnaces, Fire Boxes, Combustion Chambers. Part I. Calculation of Radiation from. Solids and Gas Volumes by the Laws of Radiation from. International Journal of Advanced Engineering Research and Science, 3, 44-48.
- 10. Makarov, A.N. (2016) Modeling of a Torch and Calculation of Heat Transfer in Furnaces, Fire Boxes, Combustion Chambers. Part II. Calculation of Radiation from Gas Volumes by the Laws of Radiation from Cylinder Gas Volumes. International Journal of Advanced Engineering Research and Science, 3, 49-54.
- 11. Makarov, A.N. (2015) Laws of Heat Radiation from Surfaces and Gas Volumes. Word Journal of Engineering and Technology, 3, 260-270.
https://doi.org/10.4236/wjet.2015.34027 - 12. Makarov, A.N. (2015) Laws of Radiation From Large Gas Volumes and Calculation of Heat Transfer in Steam Boiler Boxes. Mechanical Engineering Research, 5, 42-55.
- 13. Makarov, A.N. (2014) Theory of Radiative Heat Exchange in Furnaces, Fire Boxes, Combustion Chambers Is Replenished by Four New Laws. Science Discovery, 2, 34-42.
https://doi.org/10.11648/j.sd.20140202.12 - 14. Makarov, A.N. (2017) Laws of Heat Radiation from Spherical Gas Volumes. Part I. Laws Formulation. International Journal of Advanced Engineering Research and Science, 4, 74-79.
- 15. Makarov, A.N. (2017) Laws of Heat Radiation from Spherical Gas Volumes. Part II. Modeling of Heat Radiation from Volume Bodies by Radiation from Spherical and Cylindrical Gas Volumes. International Journal of Advanced Engineering Research and Science, 4, 80-87.
- 16. Makarov, A.N. (2016) Calculation of Heat Transfer in Torch Furnaces by Gas Volume Radiation Laws. World Journal of Engineering and Technology, 4, 488-503.
https://doi.org/10.4236/wjet.2016.43049 - 17. Makarov, A.N. (2016) Flare Temperature and Nitrogen Oxide Emission Reduction in the TGMP-314 I Steam Boiler Firebox. Power Technology and Engineering, 50, 200-203.
https://doi.org/10.1007/s10749-016-0683-x - 18. Makarov, A.N. (2014) Heat Transfer in Electric Arc and Torch Metallurgy Furnaces and Energy Plants: Textbook. Lan, St-Petersburg, 384 p.
- 19. Makarov, A.N. (2014) Regularities Pertinent to Heat Transfer between Torch Gas Layers and Steam Boiler Firebox Waterwalls. Part I. Geometrical and Physical Torch Model as a Source of Heat Radiation. Thermal Engineering, 61, 642-648.
https://doi.org/10.1134/S004060151406007X - 20. Makarov, A.N. (2014) Regularities Pertinent to Heat Transfer between Torch Gas Layers and Steam Boiler Firebox Waterwalls. Part II. Gas Layers Radiation Laws and the Procedure for Calculating Heat Transfer in Furnaces, Fire Boxes, and Combustion Chambers Developed on the Basis of These Laws. Thermal Engineering, 61, 717-723.
https://doi.org/10.1134/S0040601514100073 - 21. Makarov, A.N. (2014) Regularities Pertinent to Heat Transfer between Torch Gas Layers and Steam Boiler Firebox Waterwalls. Part III. Examples of Heat Transfer Calculation in Torch Furnaces and Steam Boiler Fireboxes. Thermal Engineering, 61, 814-821.
https://doi.org/10.1134/S0040601514110056