Journal of Electronics Cooling and Thermal Control
Vol.07 No.03(2017), Article ID:77831,15 pages
10.4236/jectc.2017.73006
Fabrication and Characterization of PLD-Grown Bismuth Telluride (Bi2Te3) and Antimony Telluride (Sb2Te3) Thermoelectric Devices
Ibrahim M. Abdel-Motaleb*, Syed M. Qadri
Department of Electrical Engineering, Northern Illinois University, DeKalb, IL, USA

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: May 23, 2017; Accepted: July 18, 2017; Published: July 21, 2017
ABSTRACT
We report on the fabrication and characterization of multi-leg bismuth telluride (Bi2Te3) and antimony telluride (Sb2Te3) thermoelectric devices. The two materials were deposited, on top of SiO2/Si substrates, using Pulsed Laser Deposition (PLD). The SiO2 layer was used to provide insulation between the devices and the Si wafer. Copper was used as an electrical connector and a contact for the junctions. Four devices were built, where the Bi2Te3 and Sb2Te3 were deposited at substrate temperatures of 100˚C, 200˚C, 300˚C and 400˚C. The results show that the device has a voltage sensitivity of up to 146 μV/K and temperature sensitivity of 6.8 K/mV.
Keywords:
Thermoelectric Devices, Bismuth Telluride, Bi2Te3, Antimony Telluride, Sb2Te3, Pulsed Laser Deposition, PLD, Seebeck Effect

1. Introduction
Thermoelectric devices can convert heat to electrical power and vice versa. These devices can be used for many applications, such as micro-cooling and micro-heating. The devices can also be used for converting wasted heat energy from factories, plants, and automobiles to electrical power. Micro-heating and cooling and electrical current generation can be attractive for applications such as powering biomedical sensors, cooling integrated circuits, or operating microelectromechanical systems (MEMS) devices and sensors.
Thermoelectric devices can be characterized by measuring several parameters that correlate the electrical signals (current and voltage) to the temperature difference. The first parameter used to characterize materials and devices is Seebeck coefficient. This coefficient relates the difference in voltage, ΔV, to the difference in temperatures, ΔT, between two points [1] [2] . In this case, Seebeck coefficient is a characteristic of the materials. Seebeck coefficient, S, can be expressed as:
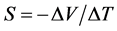 (1)
(1)
For a device composed of two dissimilar materials (A and B) forming two junctions at their ends, Seebeck coefficient relates ΔV and ΔT of the junctions. Hence,
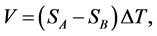 (2)
(2)
where SA and SB are Seebeck coefficients for materials A and B, respectively. In this case, the effective Seebeck coefficient for the device is
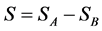 (3)
(3)
To characterize the thermoelectric performance, Altenkirch found that a dimensionless figure of merit can provide a better indication of the thermoelectric quality of a material than Seebeck or Peltier effects [1] [2] [3] . This figure of merit, ZT, can be expressed as
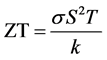 , (4)
, (4)
where σ, S, and k are the electrical conductivity, Seebeck coefficient, and thermal conductivity of the material, respectively. From Equation (3), it can be observed that a material with good thermoelectric properties should have high σ, high S, and low k.
For a device built using n-type and p-type materials, the figure of merit, ZT, can be obtained from the following Equation [1] :
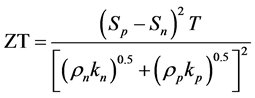 , (5)
, (5)
where Sn, ρn, and kn are the Seebeck coefficient, the resistivity, and the thermal conductivity of the n-type material, respectively. Similarly, Sp, ρp, and kp are the Seebeck coefficient, the resistivity, and the thermal conductivity for the p-type material, respectively. As indicated by Equation (3), for thermoelectric devices, the Seebeck coefficient of the device is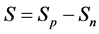 .
.
There are many different materials that can be used to build thermoelectric devices. Chalcogenides group is one type of these thermoelectric materials. They are materials that contain one or more elements such as S, Se or Te as a substantial constituent, such as CsBi4Te6, Tl2SnTe5 and Tl2GeTe5, PbTe, and ZfTe5 [4] [5] [6] [7] . Skutterudites, such as (CeyFe1−y)xCo4−x, form another set of materials. It was reported that this material has a figure of merit of 1.4 at 1000 K [1] . Half Heusler alloys, such as Zr0.5Hf0.5NiSbxSn1−x, were investigated and found to have S = 10 µ/K, at 50 K [8] . Clathrates materials, such as Eu8Ga16Ge30 and Sr8Ga16Ge30, were found to have low thermal conductivity, which results in high figure of merit [9] [10] . Alloys of Te-Ag-Ge-Sb, which is referred to as TAGS, can provide ZT > 1 [11] [12] . Ca3Co4O9 and single-crystal NaCo2O4 achieved Seebeck coefficient value of 130 and 100 μV/K, respectively [13] [14] .
One of the most promising materials for thermoelectric application is Bismuth telluride (Bi2Te3) and Antimony telluride (Sb2Te3) [15] . Bi2Te3 is a natural n-type material while Sb2Te3 is a natural p-type material [16] . These materials can be grown using many growth techniques such as Chemical Vapor Epitaxy (CVD), sputtering, Molecular Beam Epitaxy (MBE), among other techniques. Shaik and Abdel-Motaleb have grown Bi2Te3 and Sb2Te3 using Pulsed Laser Deposition (PLD) technique [17] . They have also investigated their electrical and optical characteristics [18] [19] . They have shown that good quality of polycrystalline materials of Bi2Te3 and Sb2Te3 can be grown using PLD.
In this paper, we designed and fabricated thermoelectric devices using PLD- grown 4-pair legs of n-Bi2Te3 and p-Sb2Te3. The thermoelectric properties of the materials and the devices are investigated. To the best of our knowledge, there is very few published report about the fabrication of a multi-leg, PLD-grown Bi2Te3 and Sb2Te3 thermoelectric devices. In fact, we could not identify one credible report. Therefore, we believe that this study will advance the state of the art of this area.
2. Device Design
The thermoelectric device consists of an n-type and a p-type material connected electrically in series and thermally in parallel. The materials used in this device are n-type Bi2Te3 and p-type Sb2Te3, with copper acting as the metal contact between the two materials. The devices were built on a 3-inch p-Si wafer, with 3000˚A of thermally grown SiO2 on top [20] . The SiO2 is used just for isolating the devices from the p-Si wafer. The dimensions of each area of the Bi2Te3 and Sb2Te3 are 0.4 inch × 0.12 inch. Both materials have 8 regions connected with copper contacts as shown in Figure 1(a). In this figure, the red is Bi2Te3, the blue
Figure 1. The thermoelectric device. (a) The masks for the tree layers: the red is for the Bi2Te3, the blue is for Sb2Te3, and the green is for the copper metal. (b) A photograph of the device after fabrication.
is for Sb2Te3 and the green color depicts and copper metal. The dimensions for the copper are roughly 0.34 inches × 0.12 inches.
Bi2Te3 and Sb2Te3 were grown using the PLD technique. The copper connections were deposited using the electron beam evaporation technique. Three different shadow masks for Bi2Te3, Sb2Te3 and the copper were designed and manufactured for the use in building the devices; see Figure 1(a). The finished thermoelectric device is shown in Figure 1(b).
3. Material Deposition
Bi2Te3 and Sb2Te3 were deposited using Neocera-PLD system [21] . After loading the substrate and mounting the targets for the two materials, the turbo pump was turned on to reduce the pressure to the level of 10−6 Torr. The substrate temperature was maintained to the set value using a 3-inch heater. The heater is capable of reaching a maximum temperature of 850˚C. The deposition of Bi2Te3 and Sb2Te3 was carried out in Argon atmosphere. In this study, four devices were fabricated by depositing these materials at substrate temperatures of 100˚C, 200˚C, 300˚C, and 400˚C. The deposition targets used in the PLD system are 99.999% pure hot pressed Bi2Te3 and Sb2Te3 with a diameter of 1-inch and a thickness of 0.125-inch each.
After the chamber was pumped down to about 5 × 10−6 Torr, Ar gas was admitted to increase the chamber pressure to the desired deposition pressure of 7.5 mTorr. The substrate temperature increased from room temperature to the required temperature by ramping the heater at 10˚C/minute. KrF laser was applied to the target for 2 hours for a total of 72,000 pulses. The laser beam parameters were set to the following values: incident angle equal 45˚, frequency equal 10 Hz, and energy equal 250 mJ. The targets were set to rotate during the deposition in order to reduce exfoliation.
For each device, both Bi2Te3 and Sb2Te3 were deposited at the same substrate temperature. During the deposition, the substrate was covered with its respective shadow mask to form the desired device geometry. Copper metal contacts were deposited using the electron beam evaporation technique and patterned using the shadow mask designed for this purpose.
4. Material Characterization
Dektak profilometer was used to measure the thickness of the deposited films. With a vertical resolution of ~5 A. The average thickness was found to be 400 µm for all films, as intended.
The surface morphology of Bi2Te3 and Sb2Te3 films were characterized using HITACHI S-4500 Scanning Electron Microscope (SEM). The SEM images of the device were obtained by firing the electron beam at 3 kV. Images with magnification of 2.5 K were taken for Bi2Te3 and Sb2Te3 films deposited at the different deposition temperature, as shown in Figure 2 and Figure 3.
Bi2Te3 deposited at 100˚C was found to be rough with irregular formation of
Figure 2. SEM images of Bi2Te3 films with magnification of 2.5 K for films deposited at substrate temperature of (a) 100˚C (b) 200˚C (c) 300˚C (d) 400˚C.
grains. The films deposited at 200˚C were found to have smoother surfaces compared to other films. For the higher temperature substrates, Bi2Te3 surfaces became rough again with large sizes of island structures. The roughness can be attributed to the high substrate temperatures that caused the grains to over grow and induce roughness [2] . Over growth could be due to the combination of small grains to from lager grains, by a process called secondary recrystallization [16] . However, for Sb2Te3 films, we found that there was not much difference seen between films deposited at 200˚C and 300˚C.
5. Measurement of Effective Seebeck Coefficient or Voltage Sensitivity
To obtain the effective Seebeck coefficient for a device, Seebeck coefficients for the constituent materials (Bi2Te3 and Sb2Te3) should be known first. The effective Seebeck coefficient for the device can then be calculated from Equation (3). Another way to obtain the effective Seebeck coefficient for the entire device is to measure it experimentally. This requires that both voltage and temperature differences be measured across the device junction. In our case, we do not have a
Figure 3. SEM images of Sb2Te3 films with magnification of 2.5 K for films deposited at substrate temperature of (a) 100˚C (b) 200˚C (c) 300˚C (d) 400˚C.
simple one junction device, but rather a more complicated multi-leg device, which requires a more elaborate technique.
In our case, the effective Seebeck coefficient was measured by applying a voltage across points 1 and 2 and measuring the temperature difference between points 3 and 4. Points 1, 2, 3, and 4 are indicated in Figure 1(a). It should be noted that points 1 and 2 are chosen for voltage application because they are the input ports of the device, where the legs are electrically connected in series. On the other hand the temperature difference was measured across junctions 3 and 4. It should be noted that the temperature difference can be measured across any two junctions, and this would still represent the temperature difference across the entire device. This is true because the device legs are thermally connected in parallel, and the temperature difference across any junctions is the same.
In our case, the voltage was supplied using a high precision voltage supply and measured using high resolution voltmeter. The temperature difference, ΔT, was measured using SA1-K (Chromega-Alomega) type thermocouple. This thermocouple can measure temperatures from −60˚C to 175˚C continuously with a time response of 0.3 seconds. This thermocouple has a silicon based cement adhesive attached to a polyimide adhesive pad. Two thermocouples were used for measuring the temperature across the junctions. One lead of the thermocouple was attached to junction 3 using the adhesive pad, while the other lead was connected to the thermal read out using a connector. After applying the desired voltage across points 1 and 2, the temperature of junction 3 was measured from the reading of the thermal read out. Similarly the temperature of junction 4 was measured using the other thermocouple. The difference between the readings of the two thermal readouts gave the temperature difference across junctions, 3 and 4.
As shown in Figure 4, the device with a material deposition temperature of 100˚C has temperature difference (ΔT) varied from 0 to 3 K for an applied voltage from 0 to 0.25 mV. The temperature difference remained almost constant when the voltage increased beyond this value. This may be due to the heat loss, resulting from thermal leakage to the substrate and radiation to the surroundings. This may also be due to the fact that none of the junctions were maintained at constant room temperature using a heat sink. As a result, the temperatures at
Figure 4. Temperature difference between the junctions when voltage is applied at the terminals of device with substrate temperatures of (a) 100˚C (b) 200˚C (c) 300˚C (d) 400˚C.
both the junctions changed simultaneously reducing the temperature difference between the junctions. However, this effect would not be prominent, if the applied voltage is kept low. For this reason, the applied voltage was maintained at low values to ensure accurate results.
For the device built with material deposition temperature of 200˚C, ΔT increased to 3.5 K when a voltage of 0.41 mV was applied. For the device built at 300˚C, ΔT increased to 4.5 K when a voltage of 0.61 mV was applied. Finally for the device deposited at 400˚C, ΔT increased to 4.5 K when 0.55 mV was applied at the terminals 1 and 2. Similar to the first device, no further increase in ΔT was observed when the voltages were increased beyond these values.
The ratio of the voltage applied to the temperature difference gives the effective Seebeck coefficient for the device, or. This ratio is the slope of the graph in Figure 4. From this Figure, it can be shown that the effective Seebeck coefficients are 93 μV/K, 100 μV/K, 146 μV/K and 132 μV/K for the devices with deposition temperatures of 100˚C, 200˚C, 300˚C and 400˚C, respectively. It was observed that the effective Seebeck coefficient increases with the increase of the substrate temperature, reaching a maxima at 300˚C, then decreases after that. The increase could be due to the decrease in the thermal conductivity of the materials at high deposition temperatures [22] . The subsequent decrease could be due to the excessive increase in the resistivity of Bi2Te3 which leads to the increase of the voltage drop outside the junction, reducing the effective ΔV. Kimi and Oh reported the fabrication of electrodeposited 196 pairs of Bi2Te3 and Sb2Te3 thin film legs thermopile [23] . They controlled the temperature difference of the thermopile and measured the voltage difference. When the temperature difference was set to 14˚C, a maximum sensitivity of 57.5 mV/K was obtained. This high value of the voltage sensitivity is attributed to the large number of pairs of legs and the size of device layers.
6. Thermal Conductivity
There are various methods used for the measurement of thermal conductivity of thin films. Among these methods are the thermal conductance, thermal diffusive, thermos-reflectance, the laser flash, and the 3ω method [24] [25] . In this work, the thermal conductivity values were taken from the literatures [24] [26] . The thermal conductivity for Bi2Te3 for different growth temperatures are shown in Table 1. For Sb2Te3, thermal conductivity values for PLD-grown films at the
Table 1. Thermal conductivity values of Bi2Te3.
same growth temperatures are hard to find in the literature. Therefore, an average value of thermal conductivity of 1.63 Wm−1・K−1 was used for all films of Sb2Te3 [27] .
7. Electrical Conductivity
The measured electrical parameters of Bi2Te3 and Sb2Te3 films, obtained using the four point probe technique, are shown in Figures 5(a)-(c). The Figure shows
Figure 5. Electrical Parameters for Bi2Te3 (a) Sheet Resistance (b) Resistivity (c) Electrical conductivity with temperature. Electrical Parameters for Sb2Te3 (d) Sheet Resistance (e) Resistivity (f) Electrical conductivity with temperature.
the effect of substrate temperature on the sheet resistance, resistivity and the electrical conductivity. The value of the sheet resistance for Bi2Te3 was found to increase with the substrate temperature, with a maximum value of 210 (Ω/□) at 400˚C. When the substrate temperature increases, grains over grow resulting in increasing the roughness and irregularities in the film. This results in increasing the sheet resistance of the film. This increase may be due to carrier scattering at the rough boundaries of the grains, which increases with the growth temperature [18] . Consequently, the resistivity increases and the conductivity decreases with increasing the substrate temperature. These findings have also been observed in references [18] [28] .
The sheet resistance was measured for Sb2Te3 films using the four point probe too. The measured values of the sheet resistance, resistivity and the electrical conductivity, as a function of the substrate growth temperature, are shown in Figures 5(d)-(f). As shown in the Figure, the resistivity of the films, and consequently the sheet resistance, changes only by about ±15% from the average value. Therefore, the sheet resistance and resistivity can be assumed to be almost constant with temperature, even though they have decreasing values. The conductivity will behave accordingly.
The resistivity of Sb2Te3 films behaves differently from Bi2Te3 films, where the resistivity remains almost constant with growth temperature. This behavior can be attributed to the finding that the grain size of PLD-grown Sb2Te3 films does not change with the temperature growth. Hence the level of scattering of the carriers at the grain boundaries is the same for all samples. The same behavior has been observed and reported by in references [18] [29] .
8. Figure of Merit and Power Factor
To the best of our knowledge there is no published report on the figure of merit of multi-leg devices built using PLD-grown Bi2Te3 and Sb2Te3. However, there are reports of calculated figure of merit when the material thin film is used individually to build the device.
The figure of merit of one pair of p-n legs thermoelectric device can be calculated using Equation (5). The values of the device effective Seebeck coefficient (voltage sensitivity) and Bi2Te3 and Sb2Te3 electrical resistivity and thermal conductivity are obtained from Sections 5, 6, and 7 above. The Seebeck values measured are for the entire 4-pair legs device. Since these devices are electrically connected in series, the Seebeck coefficient of one pair of Bi2Te3 and Sb2Te3 leg is 25% of the measured value. These values are used in our calculation of the Figure of Merit (ZT) and the Power Factor (PF), shown in Table 2. The power factor (PF) measures the performance of the device and can be obtained from the equation PF = S2σ. When calculating the PF, the effective resistivity of the two materials becomes r = rn + rp and the effective thermal conductivity becomes k = kn + kp, since the dimensions of the n region is the same as those of the p-region [30] .
Table 2. Performance parameters at different temperatures.
Table 2 shows the values of ZT and the PF of one pair of legs deposited at different growth temperatures. The two parameters for the device were calculated at room temperature. It can be observed that the figure of merit increases for the substrate temperature until 300˚C and then it decreases for the device with a substrate temperature of 400˚C. The power factor behaves exactly the same way. For devices with growth temperatures at 100˚C, 200˚C and 300˚C, the thermal conductivity of the device was found to decrease with temperature and this is accompanied by an increase in the effective Seebeck coefficient, which results in the increase in the figure of merit and the power factor of the device. The decrease for device built at 400˚C can be attributed to the slight decrease in the electrical conductivity and the effective Seebeck coefficient at that temperature.
The performance of our devices can be enhanced if more pairs of legs are used. Kimi and Oh reported the fabrication of 196 pairs of Bi2Te3 and Sb2Te3 thin film legs thermopile using electrodeposition [23] . They reported a voltage sensitivity from 57.5 mV/K for the entire device. However by dividing the reported sensitivity value by 196 (the number of pairs of legs), the value is reduced to 293 µV/K. Our voltage sensitivity values have been affected by the fact that the device was not thermally isolated and without a heat sink. This resulted in the loss of heat due to radiation and thermal conductivity. Our simulation shows that by using a heat sink, the voltage sensitivity will increase by 25% - 200% [31] .
Using Seebeck coefficient or voltage sensitivity for all types of thermoelectric devices may not provide an accurate evaluation of the performance of some types of devices. This because a device designed for cooling is different from that built for energy harvesting. The optimum parameters for one type may not be the optimum for another type. Similar to an amplifier, the characteristics for a common base configuration is different from a common emitter configuration. One has high current gain but low voltage gain and the other has higher gain for both.
The devices reported here use politer effect, not Seebeck effect. The input to our device is voltage and the output is temperature difference. Hence the device sensitivity should be temperature sensitivity ΔT/ΔV, not voltage sensitivity, which is related to Seebeck Coefficient. To differentiate between the two parameters, let us call the voltage sensitivity SV and the temperature sensitivity ST. Let us now compare the device reported in [23] by Kimi and Oh, with our device. For our device the highest value for SV is 146 µV/K for the 4 pairs of legs device fabricated at 300˚C. This means for one leg, SV = 36.5 µV/K. For Kimi and Oh device the maximum SV = 57.5 mV/K for 196 pairs. This means for a pair of legs, SV = 293 µV/K, which is higher than our device. However, if we compare the temperature sensitivity for one pair, we will find that our device has ST = 27.4 K/mV compared with Kimi and Oh device, where ST = 3.4 K/mV. This means our device is geared to obtain higher temperature sensitivity, since it is used for cooling/heating based on politer effect. On the other hand, Kimi and Oh device is geared for energy harvesting, hence it should have higher voltage sensitivity. Temperature sensitivity can be obtained from the voltage sensitivity where ST = 1/SV.
9. Conclusions
In conclusion, we report on the design and fabrication of thermoelectric devices composed of 4-pairs of legs of PLD grown n-Bi2Te3 and p-Sb2Te3 thin films. Bi2Te3 and Sb2Te3 are simple compounds, easy to synthesize and deposit, have very high conductivity, and are naturally doped. These advantages make the cost of building devices much lower than the more complex alloys.
Our study shows that these multi-leg devices have the performance that makes them attractive for cooling/heating devices. However, these devices can even provide much higher performance, if the geometry and fabrication process are optimized to serve the application targeted. The devices fabricated achieved a maximum effective Seebeck coefficient of 146 μV/K, a figure of merit of 0.03, and a power factor of 20.8 µW/m・K2.
Although the convention is to use Seebeck coefficient, the power factor, and the figure of merit to characterize any device, we believe that such parameters should not be used universally for all thermoelectric devices. The performance of a device used for energy harvesting, can be evaluated using the voltage sensitivity, SV = ΔV/ΔT. However, devices used for cooling/heating application should use temperature sensitivity ST = ΔT/ΔV, instead. Since the reported devices are designed for cooling/heating applications, temperature sensitivity represents the best indication of the device performance. For one pair of legs, our device exhibited a max ST of 27.4 K/mV compared with 3.4 K/mV for the device reported by Kimi and Oh. However, our devices have lower voltage sensitivity of 36.5 μV/K compared with 293 μV/K for the device of Kimi and Oh for one pair of legs. These results support our claim that cooling and heating devices, such as ours, should be optimized to achieve higher temperature sensitivity, while energy harvesting devices should be optimized to obtain higher voltage sensitivity.
The performance of this device can be enhanced several fold, if superlattice layers are used [32] . The enhancement in these materials is mainly attributed to the controlling of the transport of phonons and photons in the super lattice. In order to understand and confirm the results obtained by this study, a theoretical study, such as multi-physics numerical analysis, may need to be conducted [31] .
Acknowledgements
The authors would like to acknowledge Northern Illinois University and its Microelectronic Research and Development Laboratory (MRDL) for supporting this work.
Cite this paper
Abdel-Motaleb, I.M. and Qadri, S.M. (2017) Fabrication and Characterization of PLD-Grown Bismuth Telluride (Bi2Te3) and Antimony Telluride (Sb2Te3) Thermoelectric Devices. Journal of Electronics Cooling and Thermal Control, 7, 63-77. https://doi.org/10.4236/jectc.2017.73006
References
- 1. Willfahart, A. (2014) Screen Printed Thermoelectric Devices. Linköpings Universitet, SE-60174 Norrköping.
- 2. Tritt, T.M. (2002) Thermoelectric Materials: Principles, Structure, Properties, and Applications. Encyclopedia of Materials: Science and Technology, 1-11.
- 3. Nolas, G.S., Sharp, J. and Goldsmid, J. (2001) Thermoelectrics: Basic Principles and New Materials Developments. Springer, New York City.
https://doi.org/10.1007/978-3-662-04569-5 - 4. Chung, D.-Y., et al. (2000) CsBi4Te6: A High-Performance Thermoelectric Material for Low-Temperature Applications. Science, 287, 1024-1027.
https://doi.org/10.1126/science.287.5455.1024 - 5. Sharp, J.W., Sales, B.C., Mandrus, D.G. and Chakoumakos, B.C. (1999) Thermoelectric Properties of Tl2SnTe5 and Tl2GeTe5. Applied Physics Letters, 74, 21.
- 6. Dughaish, Z.H. (2002) Lead Telluride as a Thermoelectric Material for Thermoelectric Power Generation. Physica B: Condensed Matter, 322, 205-223.
https://doi.org/10.1016/S0921-4526(02)01187-0 - 7. Littleton IV, R.T., Tritt, T.M., Korzenski, M., Ketchum, D. and Kolis, J.W. (2001) Effect of Sb Substitution on the Thermoelectric Properties of the Group IV Pentatelluride Materials M1xYxTe5 (M1/4Hf, Zr and Ti). Physical Review B, 64, 121104-121107.
- 8. Uher, C., Yang, J., Hu, S., Morelli, D.T. and Meisner, G.P. (1999) Transport Properties of Pure and Doped MNiSn, M= (Zr, Hf). Physical Review B, 59, 8615-8621.
- 9. Nolas, G.S., Cohn, J.L., Slack, G.A. and Schujman, S.B. (1998) Semiconducting Ge Clathrates: Promising Candidates for Thermoelectric Applications. Applied Physics Letters, 73.
https://doi.org/10.1063/1.121747 - 10. Meng, J.F., Chandra Shekar, N.V., Badding, J.V. and Nolas, G.S. (2001) Threefold Enhancement of the Thermoelectric Figure of Merit for Pressure Tuned Sr8Ga16Ge30. Journal of Applied Physics, 89.
- 11. Snyder, G.J. and Toberer, E.S. (2008) Complex Thermoelectric Materials. Nature Materials, 7, 105-114.
https://doi.org/10.1038/nmat2090 - 12. Levin, E.M., Bud’ko, S.L. and Schmidt-Rohr, K. (2012) Enhancement of Thermopower of TAGS-85 High-Performance Thermoelectric Material by Doping with the Rare Earth Dy. Advanced Functional Materials, 22, 2766-2774.
https://doi.org/10.1002/adfm.201103049 - 13. Hu, Y.F., Sutter, E., Si, W.D. and Li, Q. (2005) Thermoelectric Properties and Microstructure of C-Axis-Oriented Ca3Co4O9 Thin Films on Glass Substrates. Applied Physics Letters, 87, Article ID: 171912.
https://doi.org/10.1063/1.2117615 - 14. Terasaki, I., Sasago, Y. and Uchinokura, K. (1997) Large Thermoelectric Power in NaCo2O4 Single Crystals. Physical Review B, Third Series, 56, R12685-R12687.
- 15. Skrabek, E.A. and Trimmer, D.S. (1995) Properties of the General TAGS System. In: Rowe, D.M., Ed., CRC Handbook of Thermoelectrics, CRC, Boca Raton, 267-275.
- 16. Shaikh, M. (2012) Structural, Electrical and Optical Characterization of Bismuth Telluride and Antimony Telluride Thin Films Deposited by Pulsed Laser Deposition. Graduate Thesis, CEET, Northern Illinois University.
- 17. Shaik, M. and Abdel-Motaleb, I.M. (2013) Effect of Substrate Temperature on PLD Grown Thin Film Bi2Te3 and Sb2Te3. IEEE EIT Conference Proceedings, Rapid City, 8-11 May 2013.
- 18. Shaik, M. and Abdel-Motaleb, I.M. (2013) Investigation of the Electrical Properties of PLD Grown Thin Film Bi2Te3 and Sb2Te3. IEEE EIT Conference Proceedings, Rapid City, 8-11 May 2013.
- 19. Shaik, M. and Abdel-Motaleb, I.M. (2013) Investigation of the Optical Properties of PLD Grown Thin Film Bi2Te3 and Sb2Te3. IEEE EIT Conference Proceedings, Rapid City, 8-11 May 2013.
- 20. Zhang, C. and Najafi, K. (2004) Fabrication of Thick Silicon Dioxide Layers for Thermal Isolation. Journal of Micromechanics and Microengineering, 14, 769-774.
https://doi.org/10.1088/0960-1317/14/6/002 - 21. Brochure for PLD System.
http://www.Neocera.com - 22. Termentzidis, K., Pokropivny, A., Woda, M., Xiong, S.Y., Chumakov, Y., Cortona, P. and Volz, S. (2012) Structure Impact on the Thermal and Electronic Properties of Bismuth Telluride by Ab-Initio and Molecular Dynamics Calculations. Journal of Physics: Conference Series, 395, Article ID: 012114.
https://doi.org/10.1088/1742-6596/395/1/012114 - 23. Kimi, M.-Y. and Oh, T.-S. (2011) Processing and Thermoelectric Performance Characterization of Thin-Film Devices Consisting of Electrodeposited Bismuth Telluride and Antimony Telluride Thin-Film Legs. Journal of Electronic Materials, 40, 759-764.
https://doi.org/10.1007/s11664-011-1562-8 - 24. Wang, H. and Sen, M. (2009) Analysis of the 3-Omega Method for Thermal Conductivity Measurement. International Journal of Heat and Mass Transfer, 52, 2102-2109.
https://doi.org/10.1016/j.ijheatmasstransfer.2008.10.020 - 25. Tsukada, T., Fukuyama, H. and Kobatake, H. (2007) Determination of Thermal Conductivity and Emissivity of Electromagnetically Levitated High-Temperature Droplet Based on the Periodic Laser-Heating Method: Theory. International Journal of Heat and Mass Transfer, 50, 3054-3061.
https://doi.org/10.1016/j.ijheatmasstransfer.2006.12.026 - 26. Mavrokefalos, A., Moore, A.L., Pettes, M.T., Shi, L., Wang, W. and Li, X. (2009) Thermoelectric and Structural Characterizations of Individual Electrodeposited Bismuth Telluride Nanowires. Journal of Applied Physics, 105, Article ID: 104318.
https://doi.org/10.1063/1.3133145 - 27. Choi, J.H., Young, D., Park, S.J., Choo, B.K. and Jang, J. (2003) Temperature Dependence of the Growth of Super-Grain Polycrystalline Silicon by Metal Induced Crystallization. Thin Film Solids, 427, 289-293.
https://doi.org/10.1016/S0040-6090(02)01150-1 - 28. Chen, C.-L., Chen, Y.-Y., Lin, S.-J., Ho, J.C., Lee, P.-C., Chen, C.-D. and Harutyunyan, S.R. (2010) Fabrication and Characterization of Electrodeposited Bismuth Telluride Films and Nanowires. The Journal of Physical Chemistry C, 114, 3385-3389.
https://doi.org/10.1021/jp909926z - 29. Pradyumnan, P.P. and Swathikrishnan (2010) Thermoelectric Properties of Bi2Te3 and Sb2Te3 and Its Bilayer Thin Films. Indian Journal of Pure & Applied Physics, 48, 115-120.
- 30. Lee, H., Attar, A. and Weera, S. (2015) Performance Prediction of Commercial Thermoelectric Cooler Modules Using the Effective Material Properties. Journal of Electronic Materials, 44, 2157-2165.
https://doi.org/10.1007/s11664-015-3723-7
http://homepages.wmich.edu/~leehs/ME695/Thermoelectric%20Coolers%20for%20class.pdf - 31. Abdel-Motaleb, I. and Qadri, S. Multi-Physics Numerical Simulation of Thermoelectric Devices. (In Preparation)
- 32. Venkatasubramanian, R., Siivola, E., Colpitts, T. and O’Quinn, B. (2001) Thin-Film Thermoelectric Devices with High Room-Temperature Figures of Merit. Nature, 413, 597-602.







