Journal of Electronics Cooling and Thermal Control
Vol.06 No.04(2016), Article ID:72861,14 pages
10.4236/jectc.2016.64013
Optimization by Thermodynamics in Time Finished of a Cold Store with Mechanical Compression of the Vapors
L. Okotaka Ebale, B. Mabiala*, D. Nkounkou Tomodiatounga
Laboratoire Mécanique, Energétique et Ingénierie, Chaire Unesco en Sciences de l’Ingénieur-Ecole Nationale Supérieure Polytechnique, Université Marien Ngouabi, Brazzaville, Congo

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 29, 2016; Accepted: December 17, 2016; Published: December 20, 2016
ABSTRACT
This study made it possible to determine by the application of thermodynamics in finished time, the points of instruction necessary to the development of a regulation system for the rationalization of the power consumption in a cold store. These points were obtained by determining the optimal variations of temperature as well to the condenser and the evaporator corresponding to the minimum capacity absorptive by the compressor for a maximum COP.
Keywords:
Thermodynamics in Finished Time, Rationalization of Energy, Maximum Refrigerating Power, Optimal Variations of Temperature

1. Introduction
Response to the demands imposed by the market, of the directives related to the rational use of energy and the safeguarding of the environment, the design of the current cold stores requires to a certain extent, taking into account of various constraints, in particular: thermodynamic constraints (minimization of the irreversibilities); technological constraints (pressure losses, losses of fluid cooling) and economic constraints (value for money) [1] . The interaction between these multi-field constraints, poses a problem of optimization which can find its resolution in the application of thermodynamics in finished time, which by definition represents the thermodynamics of the real systems whose heat transfers with the tanks (evaporator and condenser) have external irreversibilities [2] . In refrigeration industry, this problem results in the maximization of the performance of the cold store in other words, the maximization of its coefficient of performance (refrigerating COP = production/consumption [3] ). In the cold stores, the production of the real flow of heat is achieved by means of an evaporator; paradoxically, the ideal and reversible refrigerating cycle of Carnot whose refrigerating efficiency is maximum and of which the differences in temperature between the reserves and the fluid of the cycle are infinitesimal, delivers a null heat flow ( [4] [5] [6] [7] ). However, to deliver a heat flow not no-one, the heat-transferring surfaces and the time of contact with the tanks must be infinite, thus delivering a virtual refrigerating power. Obtaining a real refrigerating power, thus imposes heat-transferring surfaces and total coefficients of finished transfer, differences in temperatures with the finished tanks ( [1] [8] [9] ). Consequently, one obtains the time of contact between the fluid interns and the finished tanks. In addition, the transfer laws of heat of the two tanks make it possible to obtain heat flows according to the conductance and the differences in temperature; they easily allow the determination of the optimal values of temperature at the evaporator and the condenser for a minimal consumption of energy ( [2] [5] [7] ).
These optimal values will make it possible for the system of regulation to adapt the operation of the installation to the temperature variations for a COP maximum (refrigerating COP = production/consumption). The COP in addition expresses the viability of a refrigerating cycle. Optimization will consist in determining the optimal variation of temperature 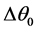 to the evaporator corresponding to a minimal consumption of energy to the compressor
to the evaporator corresponding to a minimal consumption of energy to the compressor 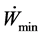 for obtaining a maximum refrigerating flow [10] [11] . The resolution of the problem will require the development of a system of equations bringing into playing the equations of the energy assessment, entropy and of heat transfer. A transformation of the sizes dimensioned into a dimensional size will facilitate the mathematical treatment of optimization of the data of the system of equations
for obtaining a maximum refrigerating flow [10] [11] . The resolution of the problem will require the development of a system of equations bringing into playing the equations of the energy assessment, entropy and of heat transfer. A transformation of the sizes dimensioned into a dimensional size will facilitate the mathematical treatment of optimization of the data of the system of equations 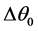 and
and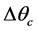 .
.
Figure 1 presents the T-S diagram of the endoreversible ideal cycle but exoirreversible, namely that one neglects the internal irreversibilities and one considers only the irreversibilities due to the differences of temperature 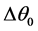 and
and 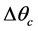 with the reserves in heat which are respectively the evaporator and the condenser. The technological and scientific interest is not only the determination of the points of instruction necessary to the development of a system regulation for the rationalization of the power consumption by the cold store using a multi-field method but especially taking into account of the irreversibilities inherent in its operation.
with the reserves in heat which are respectively the evaporator and the condenser. The technological and scientific interest is not only the determination of the points of instruction necessary to the development of a system regulation for the rationalization of the power consumption by the cold store using a multi-field method but especially taking into account of the irreversibilities inherent in its operation.
2. Material and Method
・ Material
The cold store Figure 2 is a group of production of indicated ice-cold water: STANDARD AQUACIATPOWER LD 1800BV R410A. This installation equips the refrigerating system with the air conditioning of the Bank of central Africa with Brazzaville.
Technical data of the installation:
Figure 1. Diagram T-S (T: the temperature and S: entropy).
Figure 2. Cold store AQUACIATPOWER LD 1800BV standard R410A.
・ Method for Calculation
The operation of the cold stores with mechanical compression of the vapors has for cycle of reference, the ideal cycle of reversed Carnot. In accordance with the second principle of thermodynamics: heat cannot pass from the cold source of Tf temperature to the hot spring of temperature Ta without consuming work of the external medium.
The ideal cycle of reversed Carnot is reversible as well internal as (Equation (1)) external in other words the processes of compression and of relaxation are with constant entropy and the transfer of heat between the fluid and the source is carried out with infinitesimal differences in temperature. A multi-field analysis of the refrigerating cycle of Carnot highlights the increase in the surface of transfer of heat necessary to the process of vaporization and condensation as the differences in temperature are reduced, is:
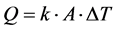 (1)
(1)
with: Exchanged total Q = heat; k = heat exchange coefficient; ∆T = difference in temperature; A = thermal heat-transferring surface.
When the transfer of heat takes place in extreme cases reversible of way, we have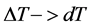 , then the heat-transferring surface
, then the heat-transferring surface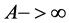 . The run time of the fluid in heat exchangers, (the condenser and the evaporator), tends towards the infinite one. Thus, for a heat-transferring surface of heat and a coefficient of exchange given, we note that the refrigerating power is cancelled.
. The run time of the fluid in heat exchangers, (the condenser and the evaporator), tends towards the infinite one. Thus, for a heat-transferring surface of heat and a coefficient of exchange given, we note that the refrigerating power is cancelled.
On the other hand, for an installation producing a real heat flow Q0 to the evaporator, the transfer of heat supposes the existence of a finished difference ∆T in temperature, the cycle of Carnot is irreversible external and the time of contact of the fluid with the sources of heat of surface A limited also has a finished value. The irreversible optimization of cycle will consist in maximizing its performance by the maximization of its coefficient of performance.
The energy assessment of the installation is given by expression (2):
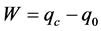 (2)
(2)
And the coefficient of performance of the installation, by Equation (3):
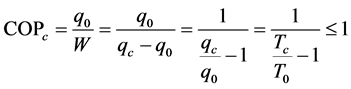 (3)
(3)
It is observed that for a mass throughput of the refrigerating agent, the energy assessment can be also written in the form of Equation (4):
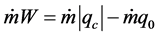 (4)
(4)
If one poses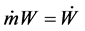 ;
;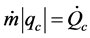 ;
;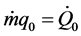 , the energy assessment becomes:
, the energy assessment becomes:
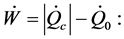 (5)
(5)
The entropic assessment as for him is written by Equation (6):

The equations of heat transfer to the evaporator and the condenser are given by expressions (7) and (8):
with 

with

From two Equations (7) and (8), it results the entropic expression (9):

The dimensional notations are declined as it follows:

The parameters to be taken into account for the optimization of the installation are the following ones:



The variables to be taken into account for the optimization of the installation are the following ones: Independent variables: 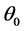



・ A dimensional refrigerating power (Equation (12)):

・ A dimensional calorific power of the condenser (Equation (13)):


・ A dimensional mechanical work is:

・ The coefficient of performance becomes:

That is to say:

By replacing the notations previously established in the entropic equations, we obtain:

However


One has:


By simplifying the room temperature of Equation (20), then by dividing the equation by the coefficient of heat exchange total K, one has:

However, 


In addition, it is known that 

In other words Equation (23), can be still written in the form:

It results from it that:

Consequently after substitution 

where 

After some simplifying transformations of the denominator 

We obtain a final expression 


Let us pose 

The value which cancels this derivative makes it possible us to obtain the maximum value and consequently the coefficient of performance 
And


By replacing 



We can express according to in the form:

What enables us to obtain:
・ minimal a dimensional calorific power (Equation (34)):

・ minimal a dimensional mechanical work (Equation (35)):
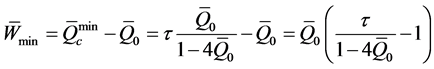
The coefficient of maximum irreversible performance of the installation (Equations (36) or (37)):


If
Carnot.
・ and the output of the installation is the report of the performance coefficient of the ideal cycle of Carnot (Equation (38)):

3. Results and Discussion
Figure 3 is represented the curve of the evolution of the coefficient of performance of the reversible cycle of Carnot of the installation according to the a dimensional temperature 
Figure 3. Evolution of the performance coefficient of the Carnot reversible cycle of the installation according to
out in an isothermal way, [5] [6] [8] . Consequently, the coefficient of performance C.O.P depends only on the a dimensional report τ = When well even the value of the C.O.P would be maximum compared to that real as Figure 3 indicates it, the refrigerating flow produced by the installation under the conditions of reversibility remains virtual [5] [6] . In opposition to the reversible cycle of Carnot, Figure 4 presents the evolution of the coefficient of performance of the irreversible cycle of Carnot of the installation whose irreversibilities caused by differences in temperature have the evaporator and with the condenser produces a real refrigerating flow, Figure 1 [1] [8] . The evolution of the COP of the installation in function de 
So that the installation produces a real heat flow 


Figure 4. Evolution of the real performance coefficient of the installation cycle according to
Figure 5. Evolution of a dimensional minimal mechanical work.
Figure 6. Evolution of the installation output compared to the Carnot cycle.
performance 

tion W to obtain is very high, the coefficient of performance is also null. To maximize the coefficient of performance in our case means a minimal consumption of energy Wmin (Equation (35)). Optimization will consist in determining the optimal variation of
Figure 7. Evolution of the dimensional minimal calorific power.
evaporator temperature corresponding to a consumption minimal of energy for obtaining flow. In substituent the dimensional optimal temperature 
4. Conclusion
It goes without saying we always seek to obtain a better coefficient of refrigerating performance of the installation while keeping in mind that it should not exceed its theoretical maximum with knowing the coefficient of performance of Carnot. It should be noted that in practice, it was noted that when the cold stores function out of their optimal operating range, they see their refrigerating power decreased because of internal and external irreversibilities. Those can even reduce the coefficient of performance to zero, thus the cold store is then likely to function without producing refrigerating power (exactly like a disconnected car). The optimal operating ranges obtained in our study (Table 1) are: for the evaporator and respectively for the condenser, a coefficient of
Table 1. Summary of the digital application of the optimization of the power station to ice-cold water.
performance 5.88. This coefficient of performance is largely higher than that is presented by the manufacturer 2.95, for the simple reason that in our study we do not take account of the losses caused by the internal irreversibilities. Lastly, to guarantee an optimal operation of the installation, the system of regulation of this one will have to be programmed according to the points of instruction of the optimal operating ranges.
Cite this paper
Ebale, L.O., Mabiala, B. and Tomodiatounga, D.N. (2016) Optimization by Thermodynamics in Time Finished of a Cold Store with Mechanical Compression of the Vapor. Journal of Electronics Cooling and Thermal Control, 6, 139-152. http://dx.doi.org/10.4236/jectc.2016.64013
References
- 1. Grosu, L. (2000) Contribution à l’optimisation thermodynamique et économique des machines à cycle inverse à deux et trois réservoirs de chaleur. Thèse de doctorat, Institut National Polytechnique de Lorraine, Université Polytechnique de Bucarest et Nancy.
- 2. Radcenco, V.T. (1994) Thermodynamique généralisée. Editura technica, Bucarest.
- 3. Tables et digrammes pour l’industrie du Froid. Institut international du Froid Juillet 1991.
- 4. Jean-Noël, F. and Julien, E. (2005) Thermodynamique, Base et Application Dunod Paris.
- 5. Doumenc, F. (2009) Elément de thermodynamique et thermique. Université de Paris VI 2009.
- 6. Mathilde, B. (2013) Reconsidération du moteur de Carno. Université de Lorraine, Nancy.
- 7. Radcenco, V.T. (1992) Eléments de thermodynamique généralisée, irréversibles en temps fini et vitesse finie. Institut polytechnique de Bucarest.
- 8. Okotaka Ebale, L. (1994) Contribution à l’étude de l’optimisation des systèmes de conditionnement de l’air. Thèse de doctorat, Université Polytechnique de Bucarest.
- 9. Institut international du froid (Ed.) (1990) Le froid et les CCF, compte rendu du colloque international de Bruxelles 1990.
- 10. Grosu, L., Feidt, M., Benelmir, R., Radcenco, V. and Dobrovicescu, A. (2000) Synthèse et perspectives des travaux relatives à l’étude thermo-économique des machine à cycle inverse. ENTROPIE no. 224/225, p. 11-18.
- 11. Grosu, L., Rochelle, P. and Martaj, N. (2000) Thermodynamique à échelle finie et optimisation du cycle de Stirling. Institut polytechnique de Lorraine, Ecole Doctorale: PROMENA 2000, Nancy.
Nomenclature
A: Heat-transferring surface
Ac: Surface of the condenser
A0: Surface of the evaporator
BEAC: Bank of the States of Central Africa
BP: Low pressure
COP: Coefficient of performance








h: Enthalpy
HR: Relative humidity
K: Coefficient of total heat exchange by convection




m: Mass throughput
P: Pressure




PMB: Dead bottom centre
PMH: Not high dead






T: Temperature
t: Time of contact of the fluid with the exchangers (evaporator and condenser)







v: Specific volume
W: Consumed mechanical energy



Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jectc@scirp.org
















