Received 1 July 2014; revised 1 August 2014; accepted 30 August 2014

ABSTRACT

Forced-air convection cooling of high-power electronic devices is widely used, but it has a problem that a rise in temperature of the air used to cool the upstream devices decreases the cooling capability for the downstream devices. In this study we made an experimental apparatus including a memory card array and measured the effect of the rise in temperature of the air on the heat transfer coefficient of the memory cards that were downstream in the air flow. Using these measurements, we devised a simple calculation model, called the thermal diffusion layer model, to calculate the heat transfer coefficient of multiple rows of memory cards. The rise in temperature of downstream memory cards due to higher temperature air can be evaluated with a parameter representing the delay of thermal mixing for air. The heat transfer coefficient calculated with the thermal diffusion layer model agreed with our experimental results.

Keywords:

Forced Convection, Heat Transfer Performance, LSI Cooling, Memory Array

1. Introduction

The heat density of high-load electronics, such as high-performance servers and the inverters used in vehicles, has been increasing as a result of higher processing speeds and higher power outputs. Focusing on the heat density of high-performance server-CPU (Central Processing Unit) modules, the trend in development since 2000 has been away from bi-polar devices and toward low-power-consumption CMOS (Complementary Metal Oxide Semiconductor) devices. However, continued demand for higher performance has reversed the trend, and the heat density of CPU modules has begun to rise again. The method used to cool electronic devices depends on the heat generation level and the operating environment, whereas the available methods include natural convection cooling [1] , forced-air convection cooling, heat pipe cooling [2] , and liquid cooling. Forced-air convection cooling is the most often used because of its practical advantages in cost, installation, and maintenance. For these reasons, we have been developing a forced-air convection cooling structure to cool multiple LSI (Large Scale Integration) packages and memory arrays that are mounted on a flat wiring board in electronic equipment. A parallel flow method is used in which the LSI packages and arrays are cooled sequentially by air that flows parallel to the wiring board. A problem with this method is that the heat from the upstream devices raises the temperature of the cooling air so that its cooling capability is decreased remarkably for the downstream devices. Yanagida [3] analyzed the temperature distribution of air after heating devices and proposed a method that used the thermal diffusion layer model to calculate temperature distribution of LSI packages on a printed wiring board. The authors developed highly efficient cooling methods using inclined strip fins and air-jet cooling methods that were not affected by an increase in the temperature of the cooling air [4] [5] . Kheirandish et al. [6] analyzed forced convective laminar flow in a channel with a heated obstacle attached to one wall. Recently, Nakayama [7] reviewed various cooling methods of electronic devices. In this work we study forced-air convection cooling of multiple rows of memory cards placed on a printed wiring board. Each memory card has many DRAM-LSIs (Dynamic Random Access Memory LSIs) mounted on both sides (Figure 1). Some studies [8] on this topic reported on the cooling performance of a single memory card, but very few have dealt with rows of memory cards.

In this study, we made an experimental memory card apparatus with four rows in the flow direction and eight rows in the parallel direction. We measured the effect of a rise in the temperature of the air on the heat transfer coefficient of the downstream memory cards. Using these measurements, we then devised a simple model for calculating the heat transfer coefficient of multiple rows of memory cards. We compared the calculation and experimental results and found their values to be in good agreement.

2. Experimental Apparatus

Figure 2 shows the experimental apparatus. The test section is placed in an acryl duct. The outside of the duct is thermally insulated with 50-mm-thick of glass wool. Cooling air from a blower flows into the test section after flow rate G and temperature T_ain are measured in chambers 1 and 2. Figure 3 shows the test section. Memory cards are four rows in the flow direction and eight rows in the parallel direction in the duct. Each memory card has five model-LSIs mounted on both sides. In the heat transfer experiment, any one of the four rows in the flow direction is replaced with heating model-LSIs and others are non-heating model-LSIs. The heating model-LSI is aluminum block with a stainless steel heater with heating rate Q of each model-LSI is 0.2 W. The surface temperature T_s of the heating model-LSI was measured with a T-type thermocouple, and the heat transfer coefficient h was obtained using Equation (1).

(1)

Here, T_ain is the inlet air temperature, and A_s is the surface area. Also, the surface temperatures of non-heating model-LSIs were measured with thermocouples. In this paper, the number of rows of memory cards in the flow

direction is expressed as N_card = 1 - 4 and number of rows of the memory LSIs in each card is expressed as N_lsi = 1 - 5.

3. Experimental Results of Temperature Rise of LSIs and Thermal Diffusion Layer Model

First, we measured the temperature rise of non-heating LSIs when they were heated by the air flow from the upstream memory card. Figure 4 shows the experimental results of the temperature rise ΔT_a of the non-heating LSIs at the N_lsi = 1 or 5 position on the downstream memory cards at the N_card = 2 - 4 positions when the heating memory card was placed at the N_card = 1 - 3 positions. Figure 5 shows the parameter α_t = ΔT_a/ΔT_m which means the delay of thermal mixing in air, ΔT_a is the measured temperature rise of the non-heating LSI, and ΔT_m is the calculated temperature rise of completely mixed air. The temperature rise ΔT_m was calculated with the air flow rate and heating rate of the LSI. When the air is not mixed completely, α_t is larger than 1. The parameter α_t decreases downstream and comes close to 1 at all heating memory card positions, N_card.

Figure 6 shows the relation between the delay of thermal mixing in air α_t and the distance from the heat source X for various heating positions and flow velocities. We can obtain the relationship between the parameter α_t and the distance from the heat source X, similar to the thermal diffusion layer model proposed by Yanagida [3] .

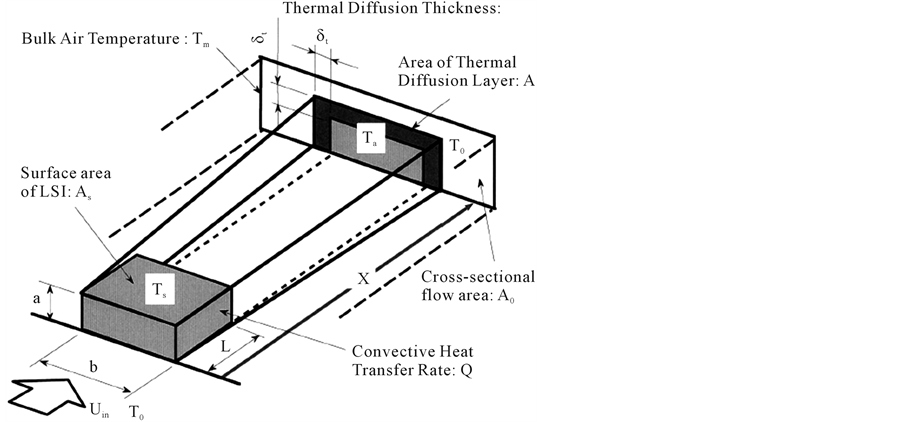
Figure 7 shows the thermal diffusion layer model for our experimental apparatus. The dimensions of the heating LSI were as follows: height a = 1 mm, width b = 21 mm, and length L = 10 mm. The area of the thermal diffusion layer A is wider than the front area of the LSI (a ´ b) by the thermal diffusion thickness δ_t. Hence, we can write A = (a ´ b) + (2a + b) ´ δ_t. The delay in thermal mixing in the air flow α_t = ΔT_a/ΔT_m can be calculated with A₀/A, where A₀ is the cross-sectional area of the air duct. The thermal diffusion thickness δ_t is proportional

to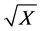, and the proportionality constant is obtained using our experimental data shown in Figure 6, as follows:

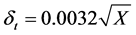(2)

The parameter α_t and the distance from the heat source X have following relationship using Equation (2):

(3)

Calculation results with Equation (3) agree with the experimental results in Figure 6.

4. Experimental Results of Heat Transfer Coefficient and Comparison with Calculation Using Thermal Diffusion Layer Model

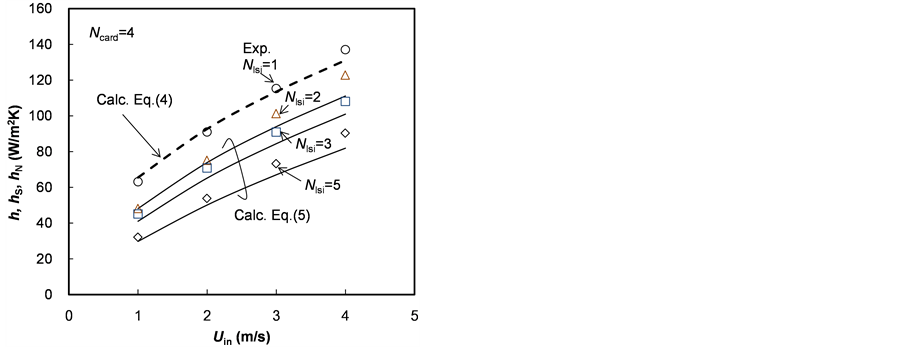
Figure 8 shows the experimental results of the heat transfer coefficient h of LSIs at the N_lsi = 1 - 5 positions on the memory card at the N_card = 1 position with a change in the inlet air velocity u_in when the heating memory card was placed at the N_card = 1 position. We see that the heat transfer coefficient h of the downstream LSIs is lower than that of the upstream LSIs, because of the temperature rise in the air flow.

The heat transfer coefficient h_S on a flat surface of a single LSI can be calculated with the following equations

[9] by using the Reynolds number,: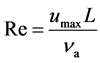

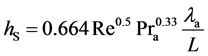(4)

Here, u_max is the air velocity above the LSI’s surface, L is the length of LSI, n_a is the dynamic viscosity of air, Pr_a is the Prandtl number of air, and l_a is thermal conductivity. The broken line in Figure 8 shows the result of calculation h_S using Equation (4), and it agrees with the experimental results of the N_lsi = 1 data.

Next, we calculated the heat transfer coefficient h_N coupled with the temperature rise in air using α_t. The heat transfer coefficient h_N can be calculated with the following equation:

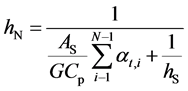(5)

Here G is the air flow rate, and C_p is the specific heat of air. The solid lines in Figure 8 show the results of the calculation h_N with Equation (5), and they agree with the experimental results of the N_lsi = 2 - 5 data.

Figure 9 and Figure 10 show the experimental results of the heat transfer coefficient h of the LSIs at the N_lsi = 1 - 5 positions on the memory cards at the N_card = 2 and 4 positions with a change in the inlet air velocity u_in when the heating memory card was placed at the N_card = 2 and 4 positions. The heat transfer coefficient h in Figure 9 and Figure 10 is almost same as that in Figure 8, and the calculations h_S, h_N using Equations (4) and (5) agree with the experimental results.

Figure 11 shows the experimental results of the overall heat transfer coefficient h_overall of the LSIs at the N_lsi = 1 and 5 positions on the memory cards at the N_card = 2 and 4 positions when all memory cards at the N_card = 1 - 4 positions are heating. The results of the calculation with Equation (5) agree with the experimental results. Therefore, the thermal diffusion layer model of Equation (5) is a precise calculation of heat transfer coefficient of multiple rows of memory cards, despite that it is very simple. Our proposal of the thermal diffusion layer model of Equation (5) is thus very practical.

5. Conclusions

We made an experimental apparatus including a memory card array and measured the effect of a rise in the temperature of air on the heat transfer coefficient of memory cards at downstream positions in the air flow. Using these measurements, we proposed a simple calculation model of the heat transfer coefficient of multiple rows of memory cards. The following results were obtained.

1) The rise in temperature of the downstream LSI resulting from a temperature rise in the air heated by an upstream heating source can be evaluated with a parameter called the delay of thermal mixing in air, α_t. The parameter α_t decreases downstream and comes close to 1 at a large distance from the heat source X and α_t does not depend on the heating position or flow velocity.

2) The heat transfer coefficient coupled with the rise in temperature of the air through the parameter α_t can be calculated with Equation (5) and the thermal diffusion layer model. The calculation agreed with the experimental results. There results indicate that the thermal diffusion layer model is a simple and precise method of calculating heat transfer coefficient of multiple rows of memory cards.

References