Journal of Electronics Cooling and Thermal Control
 Vol. 3  No. 2 (2013) , Article ID: 33063 , 9 pages DOI:10.4236/jectc.2013.32007

Air Cooling of Mini-Channel Heat Sink in Electronic Devices

Mousa M. Mohamed*, Mostafa A. Abd El-Baky

Mechanical Power Engineering Department, Faculty of Engineering, Minufiya University, Shebin El-Kom, Egypt

Email: *mousamohamed@yahoo.com

Copyright © 2013 Mousa M. Mohamed, Mostafa A. Abd El-Baky. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received January 2, 2013; revised February 2, 2013; accepted February 10, 2013

Keywords: Mini-Channel Heat Sink; Channel Air Cooling; Electronic Cooling; Fin Approach

ABSTRACT

Heat transfer experiments were conducted to investigate the thermal performance of air cooling through mini-channel heat sink with various configurations. Two types of channels have been used, one has a rectangular cross section area of 5 ´ 18 mm2 and the other is triangular with dimension of 5 ´ 9 mm2. Four channels of each configuration have been etched on copper block of 40 mm width, 30 mm height, and 200 mm length. The measurements were performed in steady state with air flow rates of 0.002 - 0.005 m3/s, heating powers of 80 - 200 W and channel base temperatures of 48˚C, 51˚C, 55˚C and 60˚C. The results showed that the heat transfer to air stream is increased with increasing both of air mass flow rate and channel base temperature. The rectangular channels have better thermal performance than triangular ones at the same conditions. Analytical fin approach of 1-D and 2-D model were used to predict the heat transfer rate and outlet air temperature from channels heat sink. Theoretical results have been compared with experimental data. The predicted values for outlet air temperatures using the two models agree well with a deviation less than ±10%. But for the heat transfer data, the deviation is about +30% to –60% for 1-D model, and –5% to –80% for 2-D model. The global Nusselt number of the present experimental data is empirically correlated as 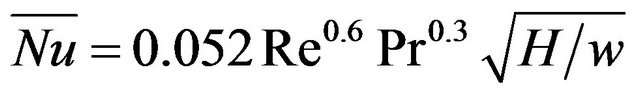with accuracy of ±20% for 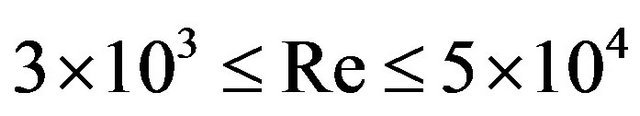and compared with other literature correlations.

1. Introduction

Traditional cooling by air is widely used in electronic devices in order to maintain it at acceptable temperature levels, e.g., below 100˚C. Recently, micro-channels heat sink is a very attractive method for high heat flux situations due to its larger area to volume ratio [1]. Because of the wide range of uses for microchannel, it is important to be able to predict their behavior both thermally and hydro-dynamically [2]. Tuckerman and Pease [3,4] developed the first microchannel water cooled heat sink, and demonstrated that extremely high power density with a heat flux as high as 7900 kW/m2 could be dissipated. Many researchers have proceeded to study flow and heat transfer in microchannel in greater detail, as reviewed by Phillips [5], and they concluded that minimum thermal resistance was achieved by designing heat sink to allow for turbulent flow conditions. A number of experimental and theoretical investigations have been performed [6-12]. Among these, cooling by heat transfer to single phase and boiling liquids flowing in microchannel is one of the promising directions. They had the potential problem of large temperature variation at the base of channel heat sink. This temperature variation can be reduced by allowing more coolant to flow through the channels. However, this will require more powerful pumping power supply, generating more noise and requiring bulkier packaging. Missaggia and Walpole [13] introduced a heat sink with alternate water flow direction in adjacent channels, known as the single layer counter flow (SLCF) microchannel heat sink. Vafai and Lu [14] postulated a new concept of double layer counter flow (DLCF) microchannel heat sink, which has two layers of heat sinks with the coolant in the top and bottom layer heat sink flows in opposite directions.

The optimization of the thermal performance of a microchannel heat sink was numerically investigated [15, 16]. Choquette et al. [17] developed and tested a computer code for finding the optimum design of microchannel heat sink. The results showed that significant reductions in the total thermal resistance were not achieved by designing for turbulent flow, in contrast, higher pumping power resulted. A single and double layer counter flow micro-channels heat sink with rectangular channels have been modeled by employing the thermal resistance network to evaluate the performance of the heat sink [18]. Optimization results showed that both the single and double layer heat sinks operating in laminar flow out performed the heat sink under turbulent flow conditions, both in heat transfer and hydrodynamic considerations. The effect of channels number on thermal performance, thermal resistance and optimal geometry has been obtained [19]. The channel depth, the channel width and the fin thickness are varied under the constraint that the channel aspect ratio should be less than 10. Among various design variables, the channel width appears to be the most crucial quantity in dictating the performance of microchannel heat sink. The effect of tip clearance on the cooling performance was presented under the fixed pumping power condition [20], and the presence of tip clearance can improve the cooling performance when tip clearance is smaller than a channel width. In most of these studies [21-26], the fin approach is an effective tool to analyze the transport of heat in the microchannel heat sink by using both one-dimension and two-dimension models for heat transfer.

The objective of the present work is to investigate the thermal performance of mini-channel heat sink with rectangular and triangular channels at various air flow rates and heating powers. The experiments were conducted in steady state at constant temperature of channel base and inlet air temperature. The heat transfer to the air flow and the heat transfer coefficient are examined. Fin approach of one dimensional, 1-D, and two dimensional, 2-D, models were used to predict the heat transfer and outlet air temperature from the channel heat sink. The experimental results were compared with the predicted ones by the two models to verify the fin approach models. An experimental correlation of global Nusselt number is targeted and compared with other literature correlations.

2. Experimental Set-Up and Procedure

The experimental facility and test section are shown in Figure 1. The compressed air was brought from two large supply air tanks with a total volume of 8.65 m3 at a discharge pressure of 8 bar. The tanks were provided with non-return valves on the supply pipes to control the pressure inside them. The air required for cooling process flows continuously from the main supply line to the test section through a steel pipe of 15.2 mm inner diameter and a control valve. The air flow rates were measured with an orifice meter which was checked for damage and calibrated before the installation. The test module was fabricated from a copper block of 200 mm length, 40 mm width and 30 mm thick. Two types of 4 parallel channels were etched on the upper face of the copper block as shown in Figure 2. The first type is rectangular channels with 18 mm in height, 5 mm in width and the plate or fin thickness is 4 mm. The second type is triangular channels with an isosceles triangle with a base of 9 mm and height of 10 mm.

An electric heater was used for heating the copper block from underneath. The heater was formed as a coil around a ceramic plate and immersed between other two ceramic plates to avoid the electric shock. The upper face of the channels was covered by a ceramic layer and bolted to decrease the tip clearance to a minimum or negligible value. The input power to the electric heater was controlled at 80, 120, 160 and 200 W with the aid of a voltmeter and an ammeter. The heating power was kept constant at certain value and the surface temperature was recorded when it became constant. The heater and heated channels were covered on the four walls by ceramic and thermal insulation to prevent leakage, and to minimize the heat transfer to the surrounding as shown in Figure 3. The air temperature was measured at inlet and outlet of test section and at three positions underneath the channels base. Thermocouples of type K were used for measuring. The thermocouples were attached to a digital multi-meter for measuring as illustrated in Figure 4. All measured values of air temperatures and channels base temperatures were recorded at steady state.

Experimental Data Reduction

The heat transfer between air flow and channels surface area can be considered as forced convection heat transfer. The top surface of its plate is insulated and the channels bases are uniformly heated and are considered at constant

Figure 1. Experimental set-up.

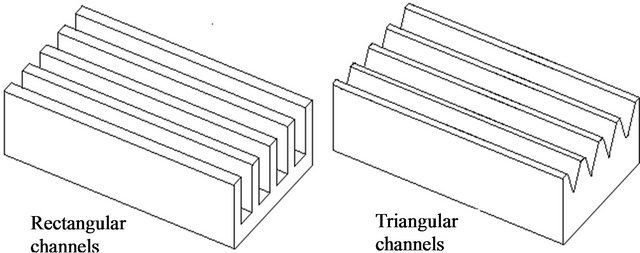
Figure 2. Test modules and channels type.

(a)(b)

Figure 3. Experimental facilities and test section.

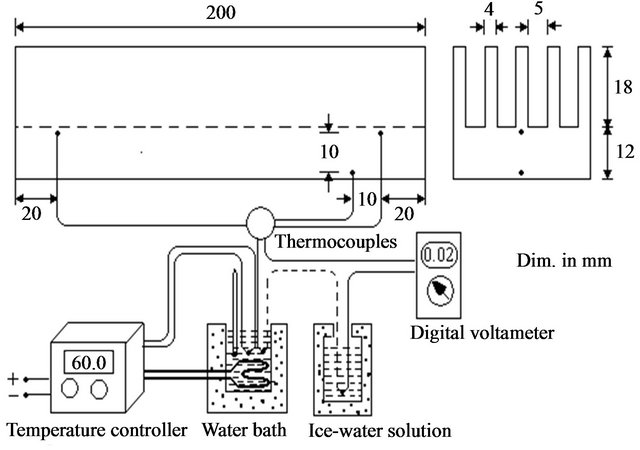
Figure 4. Thermocouples positions and rectangular channel dimensions.

temperature. The air passing through the channels absorbs heat from the heated solid surface area. The total heat transferred to the air flow can be calculated as:

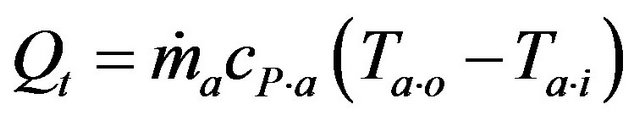(1)

Also, the average heat transfer per channel can be calculated by:

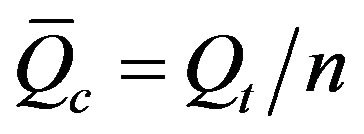(2)

where, n is the number of channels. The average heat transfer coefficient can be calculated from the heat balance between the channel heated surfaces and air flow as follows:

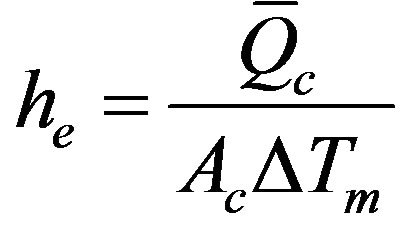(3)

where:

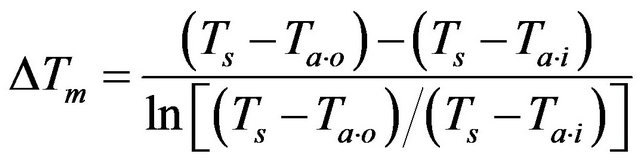(4)

The Reynolds number and the channel hydraulic diameter can be calculated as illustrated in [1,21] as follows:

(5)

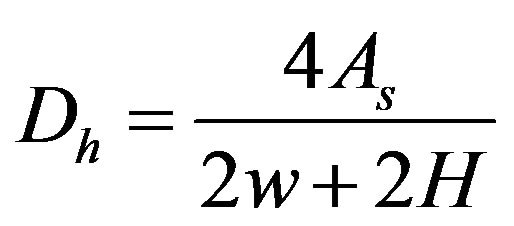(6)

The average Nusselt number based on the experimental data of average heat transfer coefficient and hydraulic diameter can be calculated as:

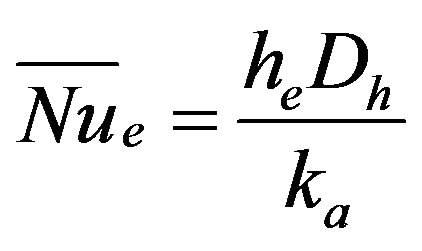(7)

The above relations were used to calculate the heat transfer coefficient and Nusselt number to investigate the effect of the channel opening ratio, 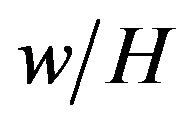, channel base temperature, and Reynolds number based on the channel hydraulic diameter on them.

3. Experimental Heat Transfer Analysis

The dimensions and channel opening ratio of the two types of channels used in this study are illustrated in Table 1. Because the upper face of the two types of channels used is insulated by ceramic and thermal insulation, the heat transfer area, Ac, in rectangular channel is the channel base surface and the two sides. But for the triangular channels, Ac is that of the two isosceles surfaces of the triangle. The opening ratio, , for rectangular channels is the ratio between the channel width to depth. But for the triangular channels, the opening ratio could be assumed as the ratio between triangle bases to its height.

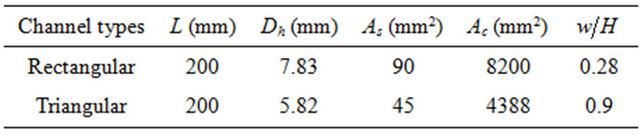
Table 1. The dimensions of the channels and their opening ratios.

The heat transfer between air flow and channel surface area at various air mass flow rates and channel base temperatures are illustrated in Figures 5 and 6. It is observed that the heat transfer to the air, 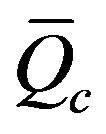, increases with increasing the air mass flow rates and channel base temperatures, Ts. Obviously, the increase in heat transfer for rectangular channel is higher than triangular channel. The results of experimental heat transfer coefficient are indicated in Figures 7 and 8. The heat transfer coefficient is increased with increasing the air mass flow rates and channel base temperature. The effect of air mass flow rates on the heat transfer coefficient is slightly positive increment, but the effect of channel base temperatures is highly positive effect.

Figure 5. Effect of air mass flow on heat transfer for rectangular channel.

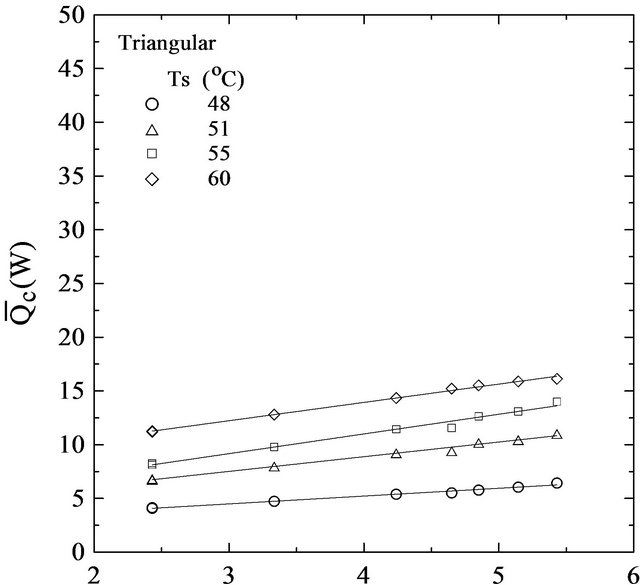
Figure 6. Effect of air mass flow on heat transfer for traingular channel.

Figure 7. Effect of air mass flow on heat transfer coefficient for rectangular channel.

Figure 8. Effect of air mass flow on heat transfer coefficient for triangular channel.

4. Mathematical Approach

The problem considered is forced convective heat flow through a rectangular channels heat sink as shown in Figure 9. Each channel has a depth H, width w, length L, and the thickness of the fin is t. The direction of fluid flow is parallel to the x-direction. The channel bottom is kept at constant temperature and provided by a constant heat flux from down, while the top surface is insulated. It is assumed that the width of the heat sink, W, is much larger than the channel width, w, and fin thickness, t. The analytical solutions of

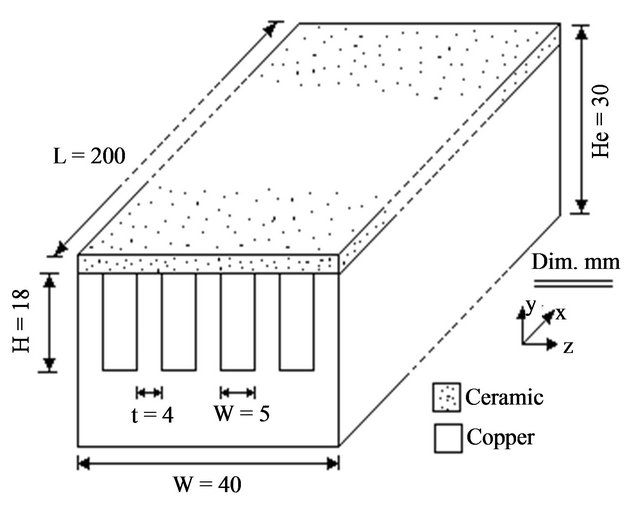
Figure 9. Rectangular channel heat sink geometry and definitions.

this problem in the literature are accomplished in two ways only for rectangular channel. The first is fin approach model and the second is porous medium model [21-25]. The interest in this work is focused on the fin approach model. So, the fin approach model in one dimension, 1-D, and two dimension, 2-D, is used in this analysis.

4.1. Fin Approach of 1-D Model

The fin approach model used is one-dimensional heat conduction in steady state conditions and the heat flux is transferred to the air flow from any point on the fin surface [27]. In this analysis, the fin tip is adiabatic and arranged in rectangular array. The total heat lost to the air flow can be calculated as:

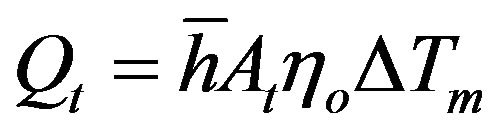(8)

where, At is the fin surface area and channel base area. The overall efficiency of the fins array is calculated as:

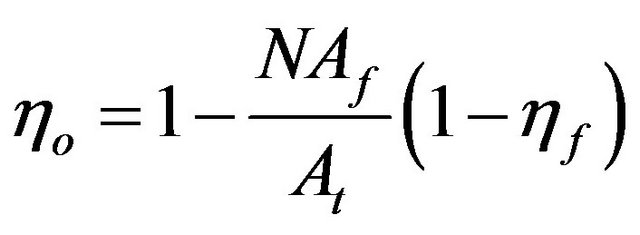(9)

The single fin efficiency is also defined as follow:

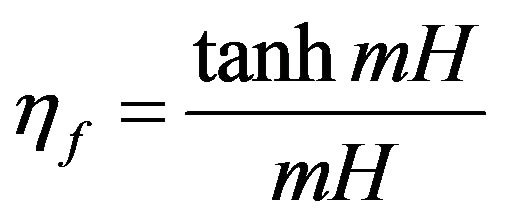(10)

The parameter m is defined as:

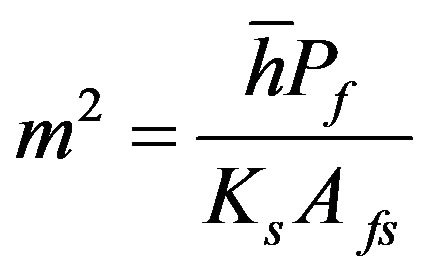(11)

The average air outlet temperature from the channel heat sink can be expressed as:

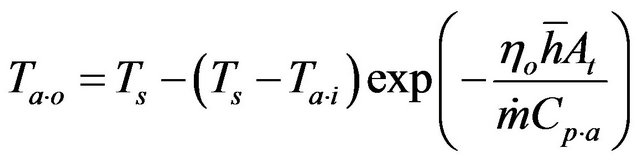(12)

For fully developed turbulent heat transfer in a channel heat sink , the conventional form of the correlations for the Nusselt number as given in [27,28] to calculate the average heat transfer coefficient, ,can be expressed as:

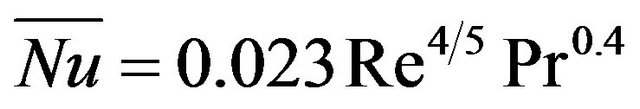(a) Ref. [24]

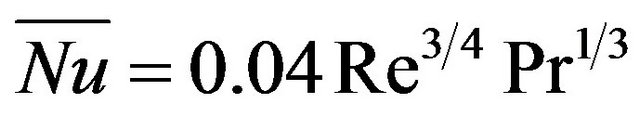(b) Ref. [21]

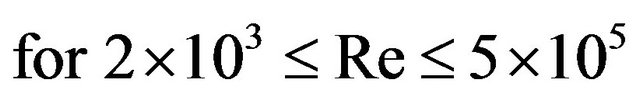(13)

4.2. Fin Approach of 2-D Model

The fin model applied to the channel heat sink is actually a one-dimensional steady state heat conduction problem [21-23] as shown in Figure 9. The air temperature is averaged over the height of channel, with. So the air temperature is the bulk mean temperature over the channel cross-section, y-direction. According to the fin model, the variation of the temperature T along the fin thickness is governed by,

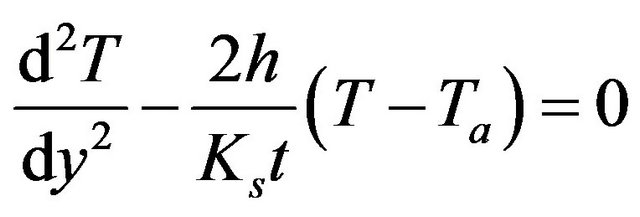(14)

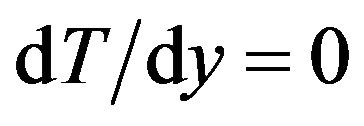where h is the interfacial heat transfer coefficient and Ks is the solid thermal conductivity. Subjected to the boundary condition at and at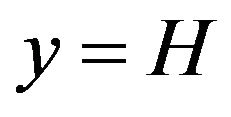, Equation (14) can be solved [21,27,29] to get the fin temperature x, y as,

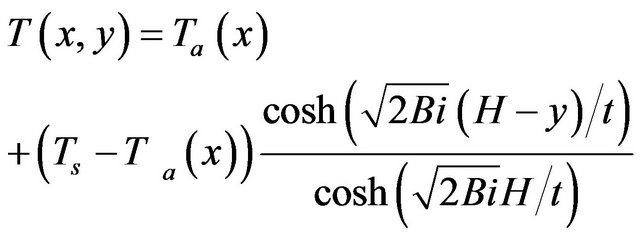(15)

The averaged fin thickness temperature is obtained as,

(16)

where is the Biot number, and the total heat lost to the cooling air per unit length of the heat sink is obtained as:

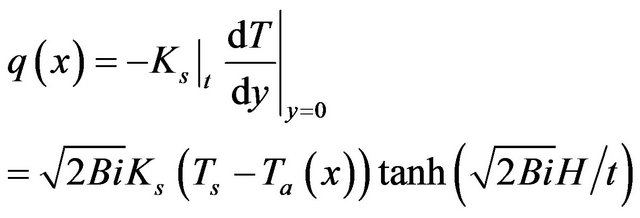(17)

The y-direction mean air temperature through the channel is obtained as,

(18)

Consequently, the average air temperature inside the channel heat sink is obtained as:

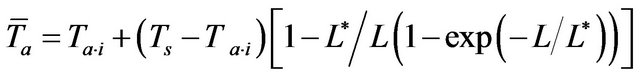(19)

where:

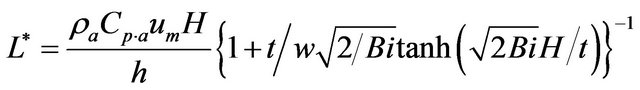(20)

The channel heat sink should not be designed to be much longer than the characteristic length scale L* [21]. A computational program was developed according to the above procedures of the two models of fin to calculate the heat transfer to the air flow and the outlet air temperature from the channels heat sink and compared it with the experimental data at the same conditions.

5. Results and Discussion

The measured heat transfer data, 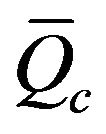, and Ta.o of the air flow are compared with the estimated ones for 1-D model which was defined by Equations (8-13), and for 2-D model which was also defined by Equations (14-20), and the comparison is illustrated in Figures 10 and 11. It was found that, the deviation between measured heat transfer data, 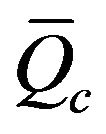, and the estimated one is about +30% to –60% for 1-D model, and +5% to –80% for 2-D model. The predicted values by 2-D model are larger than the experimental one. But for 1-D model, the predicted values are about 50% larger than the experimental data; it means that the 1-D model is more stable than 2-D model. The estimated values of 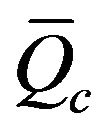by the two models used are dependent on the interfacial heat transfer coefficient, h, which was estimated from the Nusselt number by Equation (7) and Equation (13) for circular tube and air duct respectively, which may be different than the channel heat sink model. So, the two models used give different predictions for the heat transfer data. For this reason, the correlation of Nusselt number used for fully developed

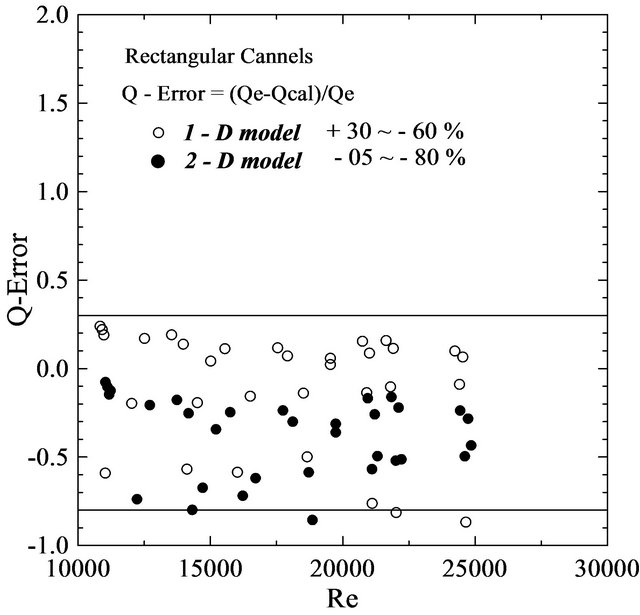
Figure 10. Deviation of measured data and calculated one for, Qc.

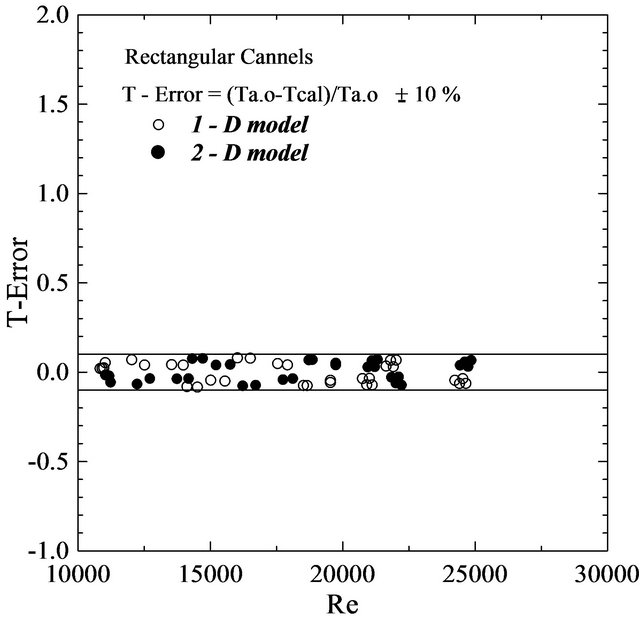
Figure 11. Deviation of measured data and calculated one for, Ta.o.

flow should be re-formulated to include the channel opening ratio,.

Fortunately, the deviation between measured data of outlet air flow temperatures from the channel heat sink and the estimated one by the two models are very close to ±10%. So, the reliability of the two models to predict the temperature gradient and average temperature of the outlet air flow is very confident as shown in Figure 11. The dependence of Nusselt number on the Reynolds number and the channel opening ratio is shown in Figure 12. The increase in the Reynolds number leads to an increase in the Nusselt number. At the same air mass flow rate, the heat transfer coefficient increased with increasing the channel base temperature. Consequently, the Nusselt number increased systematically with increasing the channel base temperature for the two types of channels used.

Present Data Correlation

Simple and purely empirical correlation for the Nusselt number of the present experimental data can be developed and compared with other literature correlations in Refs. [21,27]. The experimental heat transfer data of Nusselt number can be best correlated using the least square method with accuracy of ±20% as the followings,

(21)

The comparison of the present experimental data correlation with other literature correlations is shown in Figure 13. It is found that the deviation between the predicted data by Equation (21) and Equations 13(a) and (b)

Figure 12. Data correlation of Nusselt number.

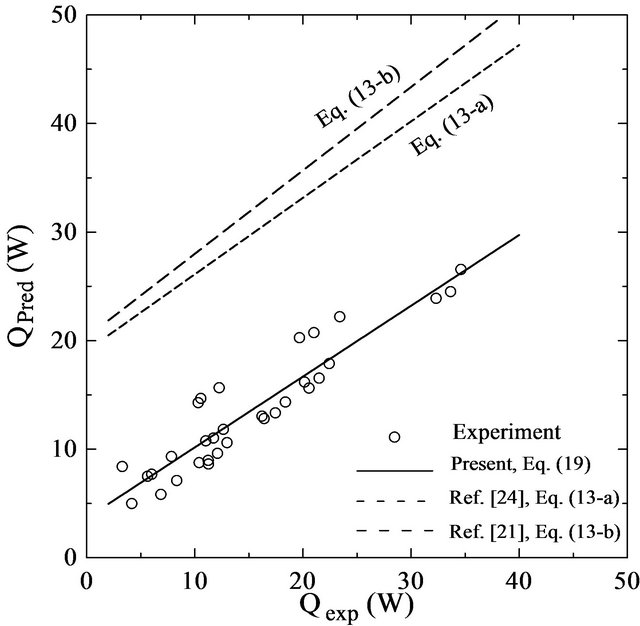
Figure 13. Comparison between the present correlation and other literature correlations.

is about 50% - 90%, because the channel opening ratio is not included in the previous correlations.

6. Conclusions

Heat transfer experiments were conducted to investigate the thermal performance of mini-channel heat sink. Two types of channels have been used with cross section areas of 5 ´ 18 mm2 for rectangular section and 5 ´ 9 mm2 for triangular section. Four channels have been etched on copper block of 40 mm width, 30 mm height, and 200 mm length. The measurements were performed at steady state with air flow rates of 0.002 - 0.005 m3/s, heating powers of 80 - 200 W, and channel base temperatures of 48˚C, 51˚C, 55˚C and 60˚C. Analytical fin approach of 1-D and 2-D models were used to predict the heat transfer and outlet air temperature from channel heat sink, and compared with experimental data. The results are summarized as follows:

1) The heat transfer to air flow is increased with increasing both of air mass flow rate and channel base temperature.

2) The rectangular channels have higher heat transfer than triangular channels at the same conditions.

3) The predicted data of outlet air temperatures from channel heat sink for the two models of fin approach are very satisfactory with accuracy less than ±10%.

4) The deviation of predicted heat transfer is about +30% to –60% for 1-D model, and –5% to –80% for 2-D model.

5) The global Nusselt number of the present experimental data is empirically correlated by least square method as, 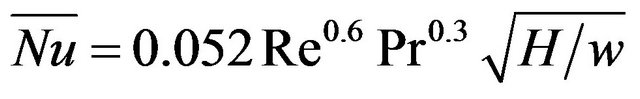for 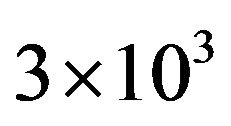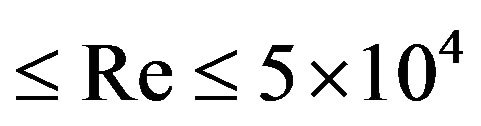with accuracy of ±20%.

6) The present data correlation is compared with other correlations, and the deviation is about 50% - 90%, because the channel opening ratio is not included in those correlations.

REFERENCES

  1. Jinliang X., Jijun Z. and Yunhua G., “Static and Dynamic Flow Instability of a Parallel Micro-Channel Heat Sink at High Heat Fluxes,” Energy Conversion and Management, Vol. 46, No. 2, 2005, pp. 313-334. doi:10.1016/j.enconman.2004.02.012
  2. M. J. Kohl, et al., “An Experimental Investigation of Microchannel Flow with Internal Pressure Measurements,” International Journal of Heat and Mass Transfer, Vol. 48, No. 8, 2005, pp. 1518-1533. doi:10.1016/j.ijheatmasstransfer.2004.10.030
  3. D. B. Tuckerman and R. F. W. Pease, “High Performance Heat Sinking for VLSI,” IEEE Electron Device Letters, Vol. 2, No. 5, 1981, pp. 126-129. doi:10.1109/EDL.1981.25367
  4. D. B. Tuckerman and R. F. Pease, “Ultrahigh Thermal Conductance Microstructures for Integrated Circuits,” Proceedings of the 32nd IEEE Electronics Components Conference, 1982, pp. 145-149.
  5. R. J. Philips, “Micro-Channel Heat Sinks,” In: A. BarCohen and A. D. Kraus, Eds., Advances in Thermal Modeling of Electronic Components and System, ASME, New York, 1990, Chapter 3.
  6. G. Hetsroni, et al., “A Uniform Temperature Heat Sink for Cooling of Electronic Devices,” International Journal of Heat and Mass Transfer, Vol. 45, No. 16, 2002, pp. 3275-3286. doi:10.1016/S0017-9310(02)00048-0
  7. Y. Cai, M. W. Wamdsganss and J. A. Jendrzejczyk, “Application of Chaos Theory in Identification of Two Phase Flow Patterns and Transitions in a Small, Horizontal, Rectangular Channel,” Journal of Fluids Engineering— ASME, Vol. 118, No. 2, 1996, pp. 383-390. doi:10.1115/1.2817390
  8. Y. P. Peles, L. P. Yarin and G. J. Hetsroni, “Steady and Unsteady Flow in a Heated Capillary,” International Journal of Multiphase Flow, Vol. 27, No. 4, 2001, pp. 577-598. doi:10.1016/S0301-9322(00)00041-0
  9. D. Brutin, F. Topin and L. Tadrist, “Experimental Study of Unsteady Convective Boiling in Heated Mini-Channels,” International Journal of Heat and Mass Transfer, Vol. 46, No. 16, 2003, pp. 2957-2965. doi:10.1016/S0017-9310(03)00093-0
  10. H. Y. Wu and P. Chenh, “Visualization and Measurements of Periodic Boiling in Silicon Microchannels,” International Journal of Heat and Mass Transfer, Vol. 46, No. 14, 2003, pp. 2603-2614. doi:10.1016/S0017-9310(03)00039-5
  11. W. L. Qu and I. Mudawar, “Flow Boiling Heat Transfer in Two Phase Micro-Channel Heat Sinks-I, Experimental Investigation and Assessment of Correlations Methods,” International Journal of Heat and Mass Transfer, Vol. 46, No. 15, 2003, pp. 2755-2771. doi:10.1016/S0017-9310(03)00041-3
  12. S. F. Wang, R. Mosdorf and M. Shoji, “Nonlinear Analysis on Fluctuation of Two Phase Flow through a T-Junction,” International Journal of Heat and Mass Transfer, Vol. 46, No. 9, 2003, pp. 1519-1528. doi:10.1016/S0017-9310(02)00455-6
  13. L. J. Missaggiaand and J. N. Walpole, “A Microchannel Heat Sink with Alternating Directions of Water Flow in Adjacent Channels,” Integrated Optoelectronics for Communication and Processing, Vol. 1582, 1992, pp. 106-111. doi:10.1117/12.135008
  14. K. Vafai and Z. Lu, “Analysis of Two-Layered Microchannel Heat Sink Concept in Electronic Cooling,” International Journal of Heat and Mass Transfer, Vol. 42, No. 12, 1999, pp. 2287-2297. doi:10.1016/S0017-9310(98)00017-9
  15. X. Yin and H. H. Bau, “Uniform Channel Micro Heat Exchangers,” Journal of Electronics Packaging, Vol. 119, No. 2, 1997, pp. 89-94. doi:10.1115/1.2792225
  16. C. Yang, D. Q. Li and J. H. Masliyah, “Modeling Forced Liquid Convection in Rectangular Microchannels with Electro-Kinetic Effects,” International Journal of Heat and Mass Transfer, Vol. 41, No. 24, 1998, pp. 4229- 4249. doi:10.1016/S0017-9310(98)00125-2
  17. S. F. Choquette, M. Faghri, M. Charmchi and Y. Asako, “Optimum Design of Microchannel Heat Sinks,” Microelectro-Mechanical Systems DSC, Vol. 59, 1996, pp. 115- 126.
  18. S. H. Chong, K. T. Ooi and T. N. Wong, “Optimization of Single and Double Layer Counter Flow Microchannel Heat Sinks,” Applied Thermal Engineering, Vol. 22, No. 14, 2002, pp. 1569-1585. doi:10.1016/S1359-4311(02)00083-2
  19. J. H. Ryu, D. H. Choi and S. J. Kim, “Numerical Optimization of the Thermal Performance of a Microchannel Heat Sink,” International Journal of Heat and Mass Transfer, Vol. 45, No. 13, 2002, pp. 2823-2827. doi:10.1016/S0017-9310(02)00006-6
  20. J. Y. Min, S. P. Jang and S. J. Kim, “Effect of Tip Clearance on the Cooling Performance of a Microchannel Heat Sink,” International Journal of Heat and Mass Transfer, Vol. 47, No. 5, 2004, pp. 1099-1103. doi:10.1016/j.ijheatmasstransfer.2003.08.020
  21. C. Y. Zhao and T. J. Lu, “Analysis of Micro-Channel Heat Sinks for Electronics Cooling,” International Journal of Heat and Mass Transfer, Vol. 45, No. 24, 2002, pp. 4857-4869. doi:10.1016/S0017-9310(02)00180-1
  22. S. J. Kim, D. Kim and D. Y. Lee, “On the Local Thermal Equilibrium in Microchannel Heat Sinks,” International Journal of Heat and Mass Transfer, Vol. 43, No. 10, 2000, pp. 1735-1748. doi:10.1016/S0017-9310(99)00259-8
  23. S. J. Kim and D. Kim, “Forced Convection in Microstructures for Electronic Equipment Cooling,” Journal of Heat Transfer—ASME, Vol. 121, No. 3, 1999, pp. 635- 645. doi:10.1115/1.2826027
  24. M, M. Mohamed, “Air Cooling Characteristics of a Uniform Square modules Array for Electronic Device Heat Sink,” Applied Thermal Engineering, Vol. 26, No. 5-6, 2006, pp. 486-493. doi:10.1016/j.applthermaleng.2005.07.013
  25. M. Beriache, A. Bettahar, H. Naji, L. Loukarfi and L. Mokhtar Saidia, “Fluid Flow and Thermal Characteristics of a Mini Channel Heat Sink with Impinging Air Flow,” Arabian Journal for Science and Engineering, Vol. 37, No. 8, 2012, pp. 2243-2254. doi:10.1007/s13369-012-0321-3
  26. X. L. Xie, W. Q. Tao and Y. L. He, “Numerical Study of Turbulent Heat Transfer and Pressure Drop Characteristics in a Water-Cooled Mini channel Heat Sink,” Journal of Electronic Packaging, Vol. 129, No. 3, 2007, pp. 247- 255. doi:10.1115/1.2753887
  27. F. P. Incropera and D. P. DeWitt, “Fundamentals of Heat and Mass Transfer,” Fourth Edition, John Wiley, New York, 1996.
  28. R. W. Knight, J. S. Goodling and D. J. Hall, “Optimal Thermal Design of Forced Convection Heat Sinks-Analytical,” Journal of Electronic Packaging—ASME, Vol. 113, No. 3, 1991, pp. 313-321. doi:10.1115/1.2905412
  29. J. P. Holman, “Heat Transfer,” McGraw-Hill Book Company, New York, 1989.

Nomenclature

Ac: channel surface area, (m2)

As: channel section area, (m2)

At: total channels surface area, (m2)

Af: fin surface area, (m2)

Afs: fin section area, (m2)

Bi: Biot number, (–)

Cp: specific heat, (J·kg–1·K–1)

Dh: channel hydraulic diameter, (m)

H: channel depth, (m)

He: copper block height, (m)

h: interfacial heat transfer coefficient, (Wm–2·K–1)

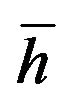: overall heat transfer coefficient, (Wm–2·K–1)

K: thermal conductivity(Wm–1·K–1)

L: channel or heat sink length, (m)

L*: characteristic length scale, (m)

: air mass flow rate, (kg·s–1)

N: fins number

: average Nusselt number, (–)

n: channels number Pf: fin perimeter, (m)

Pr: Prandtl number, (–)

Q: heat transfer rate, (W)

: average heat transfer rate, (W)

q: heat transfer per unit length, (W·m–1)

Re: Reynolds number, (–)

T: temperature, (˚C)

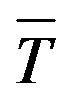: average temperature, (˚C)

t: fin thickness, (m)

um: mean air velocity through channel, (m·s–1)

W: channel heat sink width, (m)

w: channel width, (m)

hf: fin efficiency ho: overall fins efficiency m: viscosity, (N·m–2s)

r: density, (kg·m–3)

Subscript

a: air c: channel cal: calculated e: experiment f: fluid, or fin i: inlet air o: outlet air s: surface or fin metal t: total

Journal Menu >>