Journal of Electronics Cooling and Thermal Control
Vol.2 No.2(2012), Article ID:19751,3 pages DOI:10.4236/jectc.2012.22003
Analysis of Vortex Motion in Porous Media
Punjab College of Engineering and Technology, Mohali, India
Email: beantsingh7@yahoo.co.in
Received January 8, 2012; revised February 14, 2012; accepted March 5, 2012
Keywords: Porous Media; Vortex Motion; Reynolds’s Number
ABSTRACT
In vortex motion fluid moves in curve path and the stream lines are curved. When the fluid flows between curved stream line, the centrifugal forces are setup which is counter balanced by pressure forces acting in the radial direction. The vortex motion has two types of curved motion. The first type called free vortex type, the fluid moves due to its own natural effect but energy is not added to fluid when moving in curved path. The second type called forced vortex, in which energy is added to fluid. A two dimensional steady laminar free convective flow of viscous incompressible flow in porous media voids is considered. In this paper the motion of fluid is studied while moving in the porous media. It is studied that the motion of the fluid in the porous media is vortex motion at the low Reynolds’s number, where the motion is laminar motion and the fluid obeys the laws of vortex motion.
1. Introduction
The motion of fluid in casing of pump is an example of vortex motion. When considering the motion of fluid in porous media, the fluid does not moves in straight line, the fluid moves in curved direction around the porous media (spherical). Incompressible fluid between two parallel porous walls is considered [1]. Using the similarity variable, the partial differential equations were reduced to ordinary differential equations. The coupled ordinary differential equations were solved numerically using shooting method. The effect of various physical parameters, such as the Prandtl number, Grashoff number, permeability parameter and ratio of the free stream velocity to parallel wall parameter on the boundary layer velocity and skin-friction coefficient were investigated.
It is clear that the fluid velocity increased as either of the Grashoff number or permeability parameter or ratio of free stream velocity parameter to parallel wall parameter was increased.
This is also obvious that the fluid temperature decreased as either of the number, ratio of free stream velocity parameter to parallel wall motion of a fluid in bend or entrance to the pump is decreased. The motion of fluid in voids of porous media can be considered as to free vortex motion of fluid as the fluid moves due to its own natural effect and energy is not added to fluid. The geometry of porous media is complex and the width of pore is small as compared to the size of the porous media. As the fluid is saturated and single fluid flow, the motion of the fluid around the porous media can be considered as the free vortex flow at low Reynolds number.
2. Numerical Simulation
In vortex motion the stream lines are curved and when fluid flows between curved stream lines the centrifugal forces are set up and the centrifugal forces are balanced by the pressure forces acting in radial direction [2].
The Experimental investigation in walls through porous media, which has continuous influx into a horizontal wellbore configuration from the oil reservoir is incomplete. This has been recognized as one of the unsolved, yet most important problems in the production operations because of the complicated interaction between the wellbore and the reservoir.
The pressure was measured along the test wall with rectangular cross section, when the turbulent single-phase liquid flow was introduced into the channel. The fluid velocity distribution in the rectangular cross section was also measured to investigate the effect of influx on the pressure drop.
From comparison with a one-dimensional momentum exchange model, the model agreed with the experimental data for relatively low Reynolds numbers and described reasonably the flow behavior in a horizontal wellbore configuration.
Horizontal wells have become attractive for the production of thin layer reservoirs, naturally fractured reservoirs, reservoirs with gas or water coning problems, offshore environments where various wells are drilled from a central platform, and also in enhanced oil recovery practices such as steam injection, because they can improve the inflow performance of these reservoirs and produce more oil with smaller pressure drawdown as compared with conventional vertical wells due to enhancement of the reservoir contact and negative skin factors.
Depending on the completion method used in a horizontal well, fluid may enter the wellbore through perforations at various locations along the wellbore. As the distance between perforations may be insufficient to achieve a stabilized axial velocity profile, the flow pattern and the pressure gradient in a horizontal wellbore are changing along the well length [3]. Although the flow behavior in the horizontal section, with an increasing flow rate along it due to influx, and the relationship between the pressure drop and the influx from the reservoir have been recognized as one of the unsolved, yet most important problems in the production engineering, they have yet been left unqualified. In order to improve the production efficiency of a horizontal well, there are earnest demands for more information on these subjects.
Despite of the increasing number of publication pertaining to drilling and reservoir aspects of horizontal wells, a detailed literature search showed that few studies have been conducted on the flow behavior in horizontal well bores. The flow nature similar to that in horizontal well bores has been investigated in different disciplines from the petroleum engineering using channels with injection or suction from porous walls.
Yuan and finkelstein [4], performed theoretical investigation of the effect of uniform injection at the wall on two-dimensional, steady laminar flow through a porouswall pipe by solving the Navier-stokes equations both for small and large Reynolds numbers. The results showed that the injection at the porous wall increases the friction coefficient due to increased momentum exchange with the main flow. For a velocity ratio of injection to main flow at the center line equal to 0.01, the friction coefficient at the wall is increased by 70% - 80% over that for zero injection when Reynolds number exceeds 500. However, no experimental studies have been conducted on friction factors for laminar flow through porous tubes with fluid injection.
Consider equilibrium of flow in small equilibrium prisms abcd which is enclosed between two stream lines as shown in the Figure 1.
The volume of the enclosed fluid = r∙dθ∙dr per unit depth,
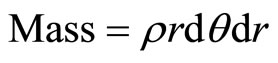 (1)
(1)
Centrifugal force act away from the centre of curvature 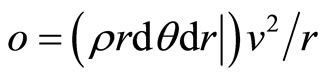
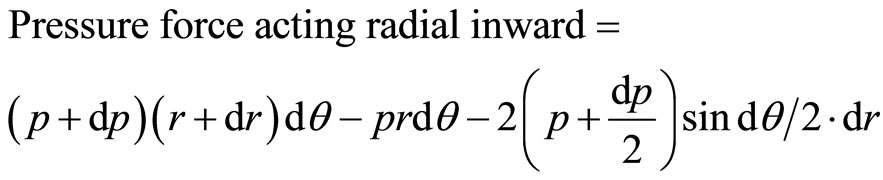 (2)
(2)
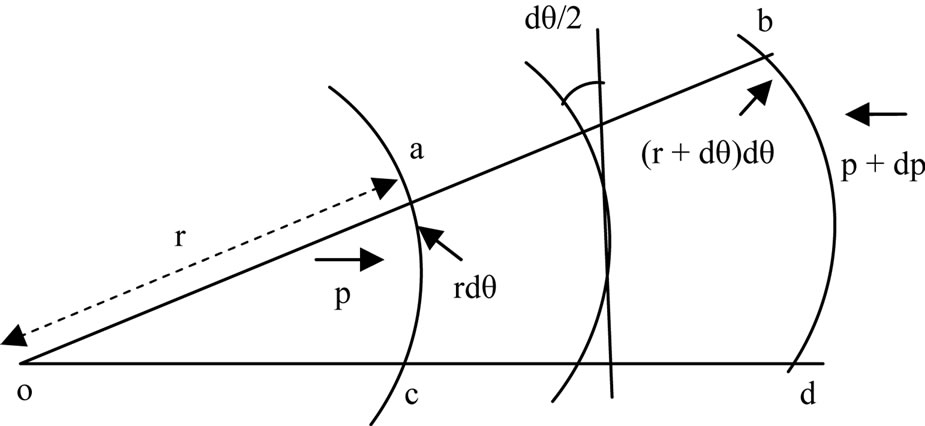
Figure 1. Curved fluid flow in two streams.
Neglect higher order small terms. Now equate the centrifugal force with pressure force,
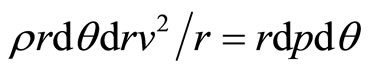 (3)
(3)
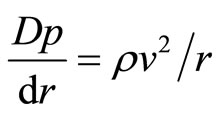 (4)
(4)
Term ρv2/r is always positive & potential gradiant dp/dr will be positive i.e. Increases with the radius, & dp/dy = −ρg (pressure increases in downward direction),
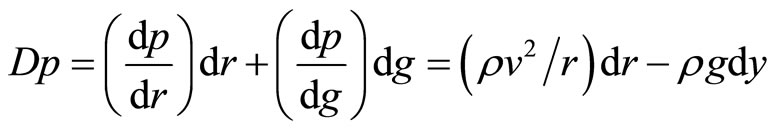 (5)
(5)
Total energy between two points at one horizontal plane,
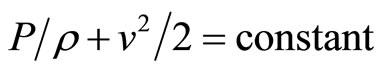 ,
,
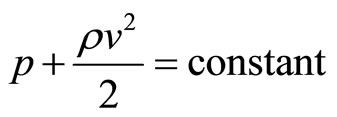 ,
,
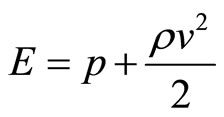 , (6)
, (6)
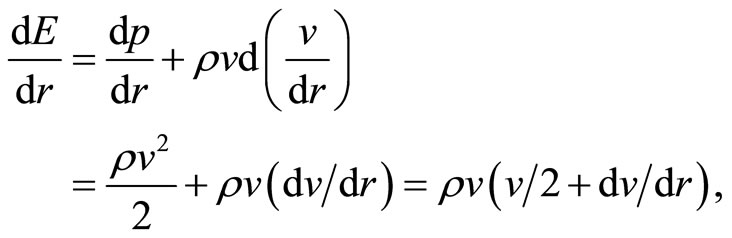
For free vortex plane dE/dr = 0,
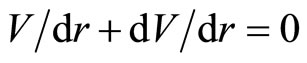 ,
,
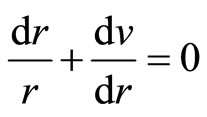 ,
,
 Rvq = constant,
Rvq = constant,
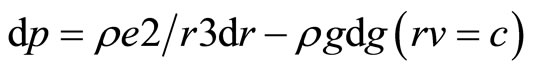 (7)
(7)
Integrating between 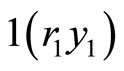 &
&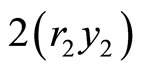 ,
,
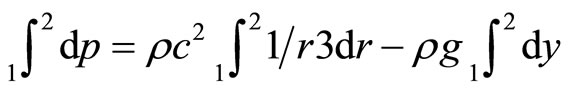 ,
,
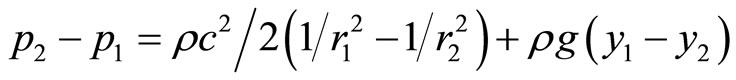 Resubstitution for
Resubstitution for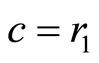 ,
, 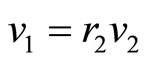 given,
given,
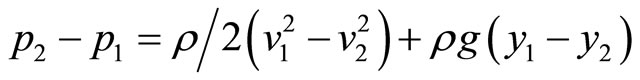 ,
,
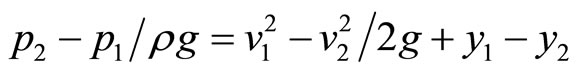 ,
,
3. Conclusion
Therefore, it is concluded that the motion of the fluid in porous media is considered as vortex motion and it obeys the equation of vortex. Further the type vortex motion is as per the velocity of the fluid and Reynold’s number.
REFERENCES
- A. M. Vaishman, “Self Similar Vortex Motion in Porous Half Space,” Fluid Dynamics, Vol. 15, 2007, pp. 140- 193. doi:10.1007/BF01089828
- D. S. Kumar, “Fluid Mechanics & Fluid Power in Engineering,” Katson Publishing House, Ludhiana.
- S. K. Nemiravskii and E. B. Sonil, “Dynamics of Coreless Vortices and Rotation Induced Dissipation Peak in Super Fluid Films on Rotating Pores Substrates,” Physical Review B, Vol. 76, No. 22, 2007, p. 224507. doi:10.1103/PhysRevB.76.224507
- S. W. Yuan and A. B. Finkelstein, “Laminar Pipe Flow with Injection and Suction through a Porous Wall,” Transactions of the American Society of Mechanical Engineers, Vol. 78, No. 4, 1956, pp. 719-724.

