Theoretical Economics Letters
Vol.06 No.06(2016), Article ID:72146,11 pages
10.4236/tel.2016.66115
Rationalizing Irrational Beliefs
Geoffrey Dunbar1,2, Ruqu Wang3, Xiaoting Wang4*
1International Economic Analysis Department, Bank of Canada, Ottawa, Canada
2Department of Economics, University of Ottawa, Ottawa, Canada
3Economics Department, Queen’s University, Kingston, Canada
4Department of Economics, Acadia University, Wolfville, Canada
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 10, 2016; Accepted: November 18, 2016; Published: November 21, 2016
ABSTRACT
In this paper we propose a “behavioral equilibrium” definition for a class of dynamic games of perfect information. We document various experimental studies of the Centipede Game in the literature that demonstrate that players rarely follow the subgame perfect equilibrium strategies. Although some theoretical modifications have been proposed to explain the outcomes of the experiments, we offer another: players can choose whether or not to believe that their opponents use subgame perfect equilibrium strategies. We define a “behavioral equilibrium” for this game; using this equilibrium concept, we can reproduce the outcomes of those experiments.
Keywords:
Centipede Game, Game Theory, Experimental Economics, Behavioral Economics

1. Introduction
In dynamic games of perfect information, the concept of subgame perfect equilibrium is most commonly used in the prediction of players’ behavior. Consider a generic game of finitely many moves, the subgame perfect equilibrium always uniquely exists. While the equilibrium concept is easily understood and the equilibrium characterization is usually straightforward, challenges to its ability to predict players’ behavior grow in the literature, both on theoretical front and experimental front.
Rosenthal [1] constructed a game (later dubbed the “Centipede Game”) that consisted of a sequence of one hundred moves. In this game, each player moves in every alternative period, either to pass (to the next period) or to end the game right away. Passing the game to the next period yields a larger total pile of money, but it strictly reduces the payoff a player receives if the opponent ends the game in her subsequent turn. The unique subgame perfect equilibrium (SPE) is that the first player ends the game at the first node and each player gets a small sum. Rosenthal argued that it is highly unlikely that, in practice, players will actually choose the SPE strategies when they play that game.
Various centipede game experiments have been conducted to test the predictive power of the concept of SPE. McKelvey and Palfrey [2] reported that only 15% of the players end the game at the first node (the outcome predicted by SPE) in a high-payoff version, and that number reduces to as little as 0.7% in other versions of the centipede game. In a much simplified two-move extensive form game, Goeree and Holt [3] documented that players usually did not trust their opponents to be rational. In contrast, Palacios-Huerta and Volij [4] conduct experiments involving expert chess players, who are known for their high degree of rationality and ability to find optimal strategies using backward induction reasoning. The outcome of their experiments is very close to the SPE prediction. Overall these experimental studies suggest that common knowledge of rationality of all players is the key requirement of SPE and so it is not surprising that players do not follow SPE strategies if they do not believe their opponents are rational.
In an attempt to reconcile the differences between the theory and the experimental outcomes, various modifications to the assumptions of the games used in the experiments have been proposed. McKelvey and Palfrey [2] , for example, propose that a player believes that the opponent is an altruist with some positive probability. They find that even a very small such probability can induce players to adopt mixed strategies in the early rounds of the game, mimicking the observed behaviors in their experiment1. A few years later, McKelvey and Palfrey [6] use a quantal choice model to re-examine the same experimental results. They show that if one assumes that the probability of implementing a particular strategy is increasing in the equilibrium payoff of the strategy, then the observed behavior more or less coincides with the predictive behavior. Zauner [7] proposes an alternative explanation of McKelvey and Palfrey’s experimental results by assuming a random perturbation of each player’s payoffs. He considers different types of perturbations and two best-fit models are selected.
In the theoretical literature, game theorists have proposed alternatives to some key assumptions that lead to SPE, including the common knowledge of rationality and backward induction. Aumann [8] formalizes the idea of higher order mutual knowledge2. Caplan [10] treats irrationality as a standard good, and players need to pay to get closer to some (irrational) “bliss belief.” Basu [11] argues that each history of moves reveals certain characteristics of players to one another, and therefore the outcomes of a game depend on these revealed characteristics (instead of depending on rationality alone). Halpern and Pass [12] propose the “iterated regret minimization” as a solution concept for strategic games. They apply it to the centipede games and find that, with linear payoffs, players will cooperate for a number of rounds. With exponential payoffs, they will cooperate all the way up to the end of the game. Meanwhile, Rand and Nowak [13] model the stochastic evolution of strategies in the centipede game and find that the players’ cooperative behavior may in fact be the favored outcome of natural selection.
Advances in psychology also help explain why players in experiments may behave differently than SPE predicts. Epstein et al. [14] conduct studies that test the cognitive-experiential self-theory. They confirm that two conceptual systems, an experiential system and a rational system, operate by their own rules of inference inside the same individual. To some extent, an individual may switch from one system to another. Tirole [15] builds on similar psychological findings and proposes a model of rational irrationality that can explain why people rehearse good news and selectively forget bad news―a universal behavior.
In this paper, we argue along the lines of the above psychological findings and propose another theoretical explanation of the failure of the SPE as a predictor of behavior. We emphasize on the observation that even if all players understand fully the concept of subgame perfect equilibrium and even if no players believe that other players are altruists, they still do not follow the SPE strategies when playing the centipede game. We assume that a player can choose to play SPE, i.e. be “rational”, or else may choose to be “behavioral”. If being “behavioral” yields a better expected outcome than being “rational”, then a player would choose to be “behavioral” (or, in terms of standard game theory terminology, “irrational”). Our intuition is as follows. SPE strategies are optimal for a player only when other players follow them. If players do not believe that other players will follow SPE strategies, then their own SPE strategies are not, in general, optimal. In the model, we specify an alternative belief for each player regarding the behavior of other players. Each player then has a choice of selecting his belief (between the SPE strategy and the alternative one) at the beginning of the game and then optimizing given the selected belief. A “behavioral equilibrium” is formed if each player is better off in the actual outcomes by selecting the alternative belief. These outcomes of the game are determined by the strategies the players actually used in the game.
The basic idea behind the “behavioral equilibrium” concept is that players can choose to believe that their counterparts can be either fully rational (such that SPE strategies are the best response) or somewhat irrational (so that SPE strategies are not best response any more). Given any belief, the players still optimize by choosing the best strategy. This is the same as in a subgame perfect equilibrium. However, the difference between a behavioral equilibrium and a subgame perfect equilibrium is that those alternative beliefs in a behavioral equilibrium do not usually coincide with those players’ actual strategies. If the two are the same, a subgame perfect equilibrium is formed. Therefore, these alternative beliefs are somewhat irrational. Still, these irrational beliefs generate better payoffs than those SPE beliefs. Thus, players will choose these irrational beliefs rationally.
The origin of irrational beliefs is an interesting and open question. Epstein et al. [14] find that there are an experiential and a rational system in each individual and that an individual can switch from one system to another. We conjecture that irrational beliefs may come from the experiential system, while rational beliefs may come from the rational system. As we observed in the above-mentioned experiments, players are better off using the irrational beliefs than the rational beliefs. These irrational beliefs may not translate into the players’ “maximum” payoffs. But the payoffs are usually very good, and are much better than the payoffs implied by SPE strategies. Therefore, players may reinforce these irrational beliefs and move away from their rational beliefs. In some sense, these irrational beliefs are the “rules of thumb” for the players.
One real life example related to the centipede games that we examine in this paper is the rotating-savings and credit associations (Roscas), commonly found in many developing countries. (See Besley et al. [16] and Anderson and Baland [17] , for example.) In these associations, a predetermined group of individuals get together and contribute a predetermined amount into a “pool” which is then given to one member (winner). These gatherings repeat themselves, with previous winners excluded from receiving the “pool” while still being obliged to contribute. The gathering may stop after each member has received the “pool” but often the same group continues the Rosca with a new “pool”. These Roscas run the risk of earlier winners defaulting on later contributions, a strategy resembling “stopping early” in the centipede game. Still, defaults are very infrequent. Our model of “irrational beliefs” or “rules of thumbs” may shed some light on these phenomena.
The rest of this paper is organized as follows. In Section 2, we analyze a few centipede games using the concept of “behavioral equilibria”. In Section 3, we analyze some of the experiments in centipede games in the literature. In Section 4, we conclude.
2. Centipede Games and Behavioral Equilibria
We begin with a general description of the centipede games.
There are two players, 1 and 2, playing the centipede game of n moves in Figure 1. To simplify notation, we assume that n is even.
In this game, 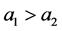 ,
, 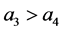 ,
,  ,
,  ,
, 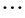 ,
, 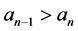 , and
, and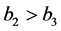 ,
, 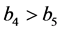 ,
, 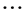 ,
, 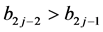 ,
, 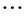 ,
, . It is straight-forward to check that the unique subgame perfect equilibrium strategy for each player is to play T whenever it is his turn to move. Given this strategy, the equilibrium outcome of the game is that player 1 plays T at the very beginning and ends the game with payoffs
. It is straight-forward to check that the unique subgame perfect equilibrium strategy for each player is to play T whenever it is his turn to move. Given this strategy, the equilibrium outcome of the game is that player 1 plays T at the very beginning and ends the game with payoffs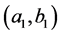 .
.
Now suppose that before the start of the game, the two players choose a belief secretly and simultaneously. Player 1 chooses a belief from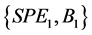 ; at the same time,
; at the same time,
Figure 1. A general n-move centipede game.
player 2 chooses a belief from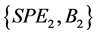 . Here,
. Here,  represents player i’s subgame perfect equilibrium belief on his opponent j’s behavior; i.e., player j will play T whenever it is his move. On the other hand,
represents player i’s subgame perfect equilibrium belief on his opponent j’s behavior; i.e., player j will play T whenever it is his move. On the other hand, 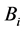 denotes player i’s alternative belief. Let
denotes player i’s alternative belief. Let 




The subgame perfect equilibrium belief 

In summary, the game we are examining is as follows. Both players simultaneously select their beliefs before the start of the game. Once the belief is selected, it remains the same throughout the game. Given these beliefs regarding an opponent’s behavior, players play the above centipede game. Each player’s goal is to maximize his expected payoff given his chosen belief.
To simplify our analysis, we assume that the beliefs are not updated during the game. (Even if we allow for belief updating, we will not get back the SPE beliefs as long as the initial belief is somewhat incorrect.)
To analyze the modified centipede game, first note the following. If 
If player 1 chooses belief 



Let 




Let 
The proposed pure strategy for player 1 is to select 




Definition 1 







where
In this behavioral equilibrium, players are better off selecting these non-SPE beliefs than selecting the SPE beliefs. These beliefs are reinforced if the players play these games again later.
Now consider mixed strategy “behavioral equilibria”. Suppose that there are more than one j’s that maximize (2), or there are more than one i’s that maximize (1), mixed strategies could be used by the players. Let 





Definition 2 







Again, in this behavioral equilibrium, players are better off selecting these non-SPE beliefs than selecting those SPE beliefs. We can generalize the concept of behavioral equilibria to any general game G with n players and normal-form payoff 
Definition 3 Suppose that 






Note that in the above definition, a player’s belief may not be correct; that is, 

Note also that the subgame perfect equilibrium strategy profile 

Below, we focus on centipede games to illustrate our equilibrium concept.
Example 1 Consider the eight-move centipede game in Figure 2.
Suppose that 








It is easy to see that 



Example 2 Consider the six-move centipede game in Figure 3.
In this game, we can construct pure-strategy behavioral equilibria similarly to the last example. Let




Now consider a mixed-strategy behavioral equilibrium. Suppose that 








that is,
Similarly, for player 2, 


Figure 2. An eight-move centipede game.
Figure 3. A six-move centipede game.
Suppose that

To construct a behavioral equilibrium, player 1’s mixed strategy 





To summarize, 





3. Analyzing Previous Centipede Game Experiments
3Payoffs 
McKelvey and Palfrey [2] report the results of seven different centipede game experiments. Sessions 1 to 3 are four-move centipede games with the following payoffs:











Table IIA in McKelvey and Palfrey [2] reports the proportion of observations at each terminal node. In that table, 


















We cannot infer a player’s belief in playing these games from the data since many different beliefs could lead to the same observed strategy. Therefore, in each session, we assume that a player’s belief corresponds exactly to his rival’s revealed strategy and calculate the player’s optimal action according to that belief. In the calculations, we assign the players a utility function with a constant degree of absolute risk aversion of 0.5 so
Table 1. Players’ strategies and optimal actions.
that the players are modestly risk averse. That is, 
4. Conclusion
In this paper, we propose a concept of behavioral equilibrium to explain the observed behavior of players in centipede games. Experimental evidence suggests that players’ behavior is inconsistent with game theoretic predictions. We allow players to abandon the “logic” of subgame perfect equilibrium and to choose an alternate belief of opponents’ expected behavior formed from previous experience in similar situations. We show that, under certain conditions, players are better off abandoning the “logic” of subgame perfect equilibrium and choosing the alternative belief instead. We argue this reinforces the players’ subjective belief that subgame perfect equilibrium may not work well in these games and, by extension, that the alternative belief becomes the belief of choice. We support our theory by re-examining the results of centipede game experiments conducted by other researchers.
Acknowledgements
We thank the referees, Jim Bergin, Lester Kwong and Jasmina Arifovic for helpful com- ments. Ruqu Wang’s research is supported by the Social Sciences and Humanities Research Council of Canada. Xiaoting Wang acknowledges support from the National Natural Science Foundation of China (#71571038).
Cite this paper
Dunbar, G., Wang, R.Q. and Wang, X.T. (2016) Rationalizing Irrational Beliefs. Theoretical Economics Letters, 6, 1219-1229. http://dx.doi.org/10.4236/tel.2016.66115
References
- 1. Rosenthal, R. (1982) Games of Perfect Information, Predatory Pricing, and the Chain Store Paradox. Journal of Economic Theory, 25, 92-100.
https://doi.org/10.1016/0022-0531(81)90018-1 - 2. McKelvey, R. and Palfrey, T. (1992) An Experimental Study of the Centipede Game. Econometrica, 60, 803-836.
https://doi.org/10.2307/2951567 - 3. Goeree, J. and Holt, C. (2001) Ten Little Treasures of Game Theory and Ten Intuitive Contradictions. American Economic Review, 91, 1402-1422.
https://doi.org/10.1257/aer.91.5.1402 - 4. Palacios-Huerta, I. and Volij, O. (2009) Field Centipedes. American Economic Review, 99, 1619-1635.
https://doi.org/10.1257/aer.99.4.1619 - 5. Gamba, A. (2013) Learning and Evolution of Altruistic Preferences in the Centipede Game. Journal of Economic Behavior & Organization, 85, 112-117.
https://doi.org/10.1016/j.jebo.2012.11.009 - 6. McKelvey, R. and Palfrey, T. (1998) Quantal Response Equilibria for Extensive Form Games. Experimental Economics, 1, 9-41.
https://doi.org/10.1023/A:1009905800005 - 7. Zauner, K. (1999) A Payoff Uncertainty Explanation of Results in Experimental Centipede Games. Games and Economic Behavior, 26, 157-185.
https://doi.org/10.1006/game.1998.0649 - 8. Aumann, R. (1992) Irrationality in Game Theory. In: Dasgupta, P., et al., Eds., Economic Analysis of Markets and Games: Essays in Honor of Frank Hahn, MIT Press, Cambridge and London, 214-227.
- 9. Samet, D. (2013) Common Belief of Rationality in Games of Perfect Information. Games and Economic Behavior, 79, 192-200.
https://doi.org/10.1016/j.geb.2013.01.008 - 10. Caplan, B. (2001) Rational Irrationality and the Microfoundations of Political Failure. Public Choice, 107, 311-331.
https://doi.org/10.1023/A:1010311704540 - 11. Basu, K. (1988) Strategic Irrationality in Extensive Games. Mathematical Social Sciences, 15, 247-260.
https://doi.org/10.1016/0165-4896(88)90010-8 - 12. Halpern, J. and Pass, R. (2012) Iterated Regret Minimization: A New Solution Concept. Games and Economic Behavior, 74, 184-207.
https://doi.org/10.1016/j.geb.2011.05.012 - 13. Rand, D. and Nowak, M. (2012) Evolutionary Dynamics in Finite Populations Can Explain the Full Range of Cooperative Behaviors Observed in the Centipede Game. Journal of Theoretical Biology, 300, 212-221.
https://doi.org/10.1016/j.jtbi.2012.01.011 - 14. Epstein, S., Lipson, A., Holstein, C. and Huh, E. (1992) Irrational Reactions to Negative Outcomes: Evidence for Two Conceptual Systems. Journal of Personality and Social Psychology, 62, 328-339.
https://doi.org/10.1037/0022-3514.62.2.328 - 15. Tirole, J. (2002) Rational Irrationality: Some Economics of Self-Management. European Economic Review, 46, 633-655.
https://doi.org/10.1016/S0014-2921(01)00206-9 - 16. Besley, T., Coate, S. and Loury, G. (1993) The Economics of Rotating Savings and Credit Associations. American Economic Review, 83, 792-810.
- 17. Anderson, S. and Baland, J.M. (2002) The Economics of Roscas and Intrahousehold Resource Allocation. Quarterly Journal of Economics, 117, 963-995.
https://doi.org/10.1162/003355302760193931
NOTES
*Corresponding author.
1In an indirect evolutionary model in which a centipede game is played in each stage, Gamba [5] shows that altruism can evolve even if preferences are unobservable.
2Samet [9] labels the material rationality in a centipede game as common belief instead of common knowledge.











