Theoretical Economics Letters
Vol.4 No.3(2014), Article ID:44516,9 pages DOI:10.4236/tel.2014.43025
Working Time Reductions and Labour Force Participation in Unemployment Contexts: A Note
Angel Martin-Roman
Department of Economic Analysis, University of Valladolid, Valladolid, Spain
Email: angellm@eco.uva.es
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 3 January 2014; revised 3 February 2014; accepted 10 February 2014
ABSTRACT
Work-sharing measures aim to reduce unemployment. When politicians are more interested in fostering this kind of measures is when the official unemployment rate published in statistics rises. There is already an important body of research addressing this issue, but it has mainly focused on the labour demand side. Nevertheless, it must not be forgotten that unemployment is determined both by demand and supply. The neoclassical model of labour supply predicts that a reduction of standard working hours encourages labour market participation. In this paper we show that this unambiguous result vanishes precisely when high unemployment makes that search transaction costs cannot be considered negligible.
Keywords:Work-Sharing, Working Time, Unemployment, Labour Supply

1. Introduction
The aim of this paper is to qualify a theoretical result related to labour supply which is relevant when economic authorities plan to reduce regulated working time in order to achieve unemployment reductions. More precisely, we are interested in analyzing the effects of work-sharing measures from a labour supply perspective. We focus on labour supply side because it has been much less studied in the literature than the demand side. Despite this, it has to be taken into account that the levels of unemployment and the unemployment rate are determined by both the labour supply and demand1. So, to evaluate and assess accurately the effects of work-sharing policies is necessary to understand workers behaviour affecting labour supply decisions, especially that related to the choice of entering the labour market or not (participation decisions).
We do believe that the relative lack of theoretical research from the labour supply side is a consequence of the influence of a strong and very well founded result which simply states that in a context of regulated working time, a reduction in the length of the standard (regulated) working week2 will always increase labour force participation. The reason for that is based on something as unquestionable as the convexity of indifference curves or the strict quasi-concavity of the utility function. Nonetheless, as we shall show later, if we add to the static neoclassical model of labour supply a simple and very reasonable assumption in unemployment contexts, such as the existence of search costs so as to find an employment, the above mentioned result will not be guaranteed.
This is particularly important because it is when the unemployment rate is very high that politicians are more interested in passing work-sharing legislation. In this way, we reckon that to take an inverse relation between regulated working time and labour force participation for granted might be a bit risky from an economic policy point of view. We also expect that our theoretical reflection encourages further empirical research that sheds light on this issue.
A number of work-sharing arrangements have been implemented in Europe during the last two or three decades. In the work of Kramarz et al. [1] there is a deep review of some of these arrangements for Germany, France, Sweden and the Netherlands (both from a theoretical and empirical point of view). Moreover, at the current time, in other European countries with high unemployment rates like Spain and Greece, work-sharing proposals (as for example an extended use of part-time contracts) are being suggested from the political arena. For all of these motives, we consider the results of this paper as being quite relevant and of current interest.
2. Background
To begin with, it is worth mentioning that the regulatory concerns in the labour market have been dominated more by regulation through prices than by regulation through quantities, by using the well-known Viscusi et al. [2] classification. Maybe, the economics of minimum wage has been the most remarkable subject in the literature associated with price regulation.
One reason that could explain the relative less attention paid to working time regulation (as compared to wage regulation, for instance) by the literature is that, in fact, in many countries working time is far from being regulated. Instead, individuals have a great deal of freedom when choosing or even bargaining over working time. Nevertheless, that is not case in continental Europe. The best way of illustrating this point is by means of a Tito Boeri’s quotation (Boeri, [3] , p. 5): “More importantly still, in Europe it is not the individual who decides how many hours to allocate to market work per week. In most of cases, it is possible to choose whether or not to work, rather than how much time to devote to work. In contrast to the USA, in most European countries there are legal limits to the total amount of work (normal plus overtime hours) and working time is tightly regulated rather than settled in the context of plant-level or individual bargaining”.
It could be said that from the work of Hart and Sharot [4] , the analysis of the relation between workers and hours time reached an important academic status and gave rise to a significant subsequent economic literature. During the 80’s several papers on this topic were published. In the early 80’s the articles of Bell [5] and Hart [6] helped to establish the grounds of the research which would blossom in the following years. Among those articles we could cite the works of Hoel and Vale [7] , Leslie [8] [9] , Calmfors and Hoel [10] [11] or König and Pohlmeier [12] . Most of these papers take what we could call the static neoclassical as the baseline model and modify it in several ways3. However, we should state that they are strongly biased towards the demand side. This kind of theoretical research inspired a number of empirical works later. We could highlight here some influential papers like Hunt [17] [18] for the German experience and Crépon and Kramarz [19] for the French case4. Despite being a literature with a long tradition, it is worth mentioning that the Great Recession has put it back in the foreground. The works of Boeri and Bruecker [21] and Burda and Hunt [22] can confirm this statement.
Regarding the labour supply side, the literature has been much less productive. Nonetheless, we may identify two lines of research. Firstly, some works have taken a collective action point of view and have studied how a monopoly union interacts with working time regulation (see the works of Calmfors [23] , Hoel [24] , Booth and Schiantarelli [25] and Booth and Ravallion [26] ). Secondly, other group of works has adopted an individual standpoint and has considered that the canonical neoclassical model of labour supply predicts unambiguously that a reduction in the number of (regulated) hours increases labour market participation. This underlying idea can be found in research papers such as Pérez-Domínguez [27] or in advanced textbooks of labour economics (see, for instance, Cahuc and Zylberberg [28] ; or Boeri and van Ours [29] ).
The main argument behind this line of reasoning is easy to understand. With time restrictions, those individuals with a strong preference for income or consumption will desire to work more hours and a reduction in regulated working time will make them to be worse-off, however none of them would quit the labour force. On the other side, some of the individuals with a relatively strong preference for leisure would be encouraged to enter the labour force with shorter working-hours. As it will be shown in the next section, this is a consequence of the convexity (to the origin) of the indifference curves or, in other words, of the strict quasi-concavity of the utility function.
This paper precisely tries to qualify this apparently clear result. The key question is that the basic structure of the neoclassical model of labour supply does not take unemployment into account; and unemployment may affect the individual’s decision making process in several ways. In this paper, we are going to focus on one of these features: the presence of non-negligible search transaction costs.
Likewise the neoclassical static model of labour demand has been profoundly modified so as to take into consideration several aspects related to working time restrictions (and this, in turn, has illustrated a variety of theoretical effects), we intend to introduce a theoretical reflection into the labour supply side here. A consideration that, we think, is very important in unemployment contexts and that changes the basic relationship (in some cases, as it will be seen) between regulated working time and labour force participation. Due to the fact that it is when unemployment is high when politicians are more interested in passing work-sharing legislation, we reckon that it necessary to address this effect so that researchers may make use of a more complete theoretical toolbox when assessing the outcomes of working time reductions, especially from an empirical standpoint.
3. The Basic Model
We shall begin with the simplest version of the model5. The main assumptions are described below.
Assumption 1. Labour force is homogeneous. We consider workers with the same skills and facing similar workplace risks. This means that wages are the same for all workers and that we leave aside the issue of wage differentials6.
Assumption 2. Working hours have a fixed length7 and are exogenously determined. This means that the individual’s possibility set consists of two points8. Moreover this supposition entails that the solution to the individual’s maximization problem is reduced to a comparison between two levels of utility9.
Assumption 3. The utility function of individuals, 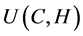 , is strictly quasi-concave. Besides we consider an additive utility function10 such as:
, is strictly quasi-concave. Besides we consider an additive utility function10 such as: , where
, where ![]() refers to consumption and
refers to consumption and 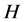 to leisure time. We suppose that marginal utilities are positive and decreasing11
to leisure time. We suppose that marginal utilities are positive and decreasing11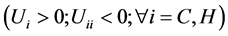 .
.
An individual will decide to supply labour if the utility index, 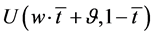 is higher than the utility index when individuals do not look for a job,
is higher than the utility index when individuals do not look for a job,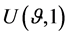 . In the utility function, consumption,
. In the utility function, consumption, ![]() , and leisure,
, and leisure,  , have been replaced by the values corresponding to such decisions. Variables can be explained as follows: w is the real wage per time unit,
, have been replaced by the values corresponding to such decisions. Variables can be explained as follows: w is the real wage per time unit, 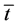 is the length of regulated working hours and
is the length of regulated working hours and ![]() is the real non-labour income. Total time has been normalized to 1 (therefore, the length of working hours,
is the real non-labour income. Total time has been normalized to 1 (therefore, the length of working hours, 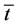 , must lie between 0 and 1). The reservation wage,
, must lie between 0 and 1). The reservation wage, 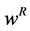 , can be defined as the wage which equal both utility indexes. That is:
, can be defined as the wage which equal both utility indexes. That is:
![]() (1)
(1)
This reservation wage admits a simple geometric interpretation: it would be equal to the slope (with opposite sign) of the line joining the point associated with non-participation in the labour market (in the consumption-leisure space) and a point yielding the same level of utility (in the same indifference curve) associated with participation, that is, a leisure level equal to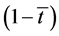 . According to Figure 1, the reservation wage would be equivalent to the slope (in absolute value) of the line
. According to Figure 1, the reservation wage would be equivalent to the slope (in absolute value) of the line![]() .
.
So as to analyze the modification of the reservation wage as a result of an exogenous change in standard (regulated) working hours, we must focus on how the both sides of the expression (1) change. First of all, it is obvious that the right hand side of (1), 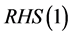 , does not change with variations in
, does not change with variations in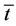 . On the other hand, the left hand side of such expression,
. On the other hand, the left hand side of such expression,  , will be modified as follows:
, will be modified as follows:
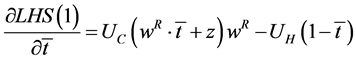 (2)
(2)
where 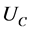 and
and 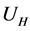 refer to marginal utilities of consumption and leisure, respectively, and they only depend on the level of consumption and leisure respectively, due to the Assumption 3. Alternatively:
refer to marginal utilities of consumption and leisure, respectively, and they only depend on the level of consumption and leisure respectively, due to the Assumption 3. Alternatively:
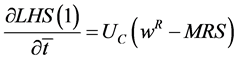 (3)
(3)
where ![]() is the Marginal Rate of Substitution between consumption and leisure.
is the Marginal Rate of Substitution between consumption and leisure. 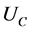 has been assessed for a level of consumption
has been assessed for a level of consumption ![]() and the MRS for the consumption-leisure pair
and the MRS for the consumption-leisure pair![]() . The
. The![]() has a simple geometric interpretation in Figure 1: the slope (in absolute value) of line
has a simple geometric interpretation in Figure 1: the slope (in absolute value) of line![]() . If the expression (3) has a negative sign, this means that a decrease (increase) of
. If the expression (3) has a negative sign, this means that a decrease (increase) of 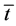 will increase (reduce) the value of such expression; to restore the equality presented in (1) a decrease (increase) in the reservation wage should occur. By observing Figure 1, it is obvious that, due to the convexity of the indifference curve, it is always true that
will increase (reduce) the value of such expression; to restore the equality presented in (1) a decrease (increase) in the reservation wage should occur. By observing Figure 1, it is obvious that, due to the convexity of the indifference curve, it is always true that 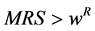 and, therefore, the expression (3) will be always negative. This implies a direct relationship between
and, therefore, the expression (3) will be always negative. This implies a direct relationship between 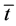 and
and 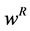 and it entails an inverse relationship between regulated working hours and labour supply.
and it entails an inverse relationship between regulated working hours and labour supply.
Result 1 (conventional wisdom): In the simple (static) neoclassical model of labour supply, there is an inverse relation between regulated working time and labour force participation. This means that work-sharing policies consisting on the reduction of regulated working hours would have an encouraging effect on the labour force.
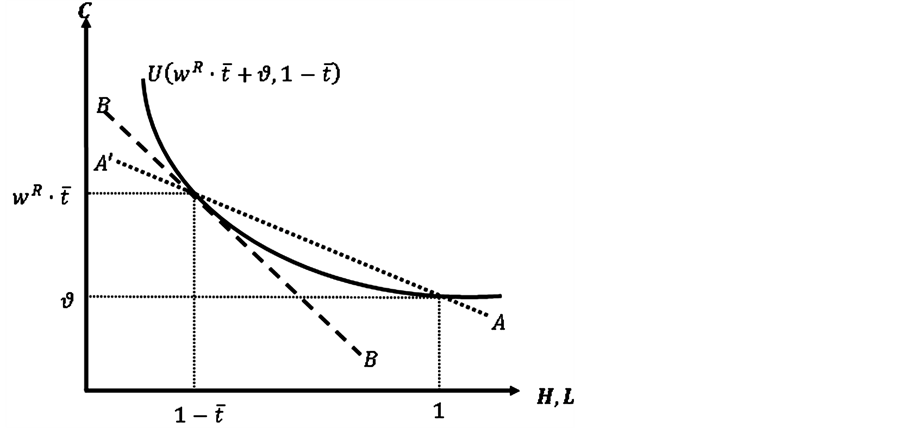
Figure 1. Reservation wage and MRS without transaction costs.
4. The Basic Model
In this section, we will show that the clear prediction established by Result 1 vanishes when individuals face search transaction costs (in terms of leisure lost) when looking for a job. In other words, assuming that before finding a job individuals have to spend some part of their leisure time in searching activities, the basic relationship between standard working hours and labour force participation becomes ambiguous. To analyse this issue, we must introduce in the model two additional assumptions.
Assumption 4. In order to make a job contact, individuals have to spend an amount of leisure time equal to![]() . After that, they sign a labour contract. This means that there is an additional cost linked to labour market participation.
. After that, they sign a labour contract. This means that there is an additional cost linked to labour market participation.
Assumption 5. The search cost is an increasing function of the unemployment rate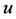 . That is
. That is 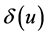 and
and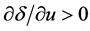 .
.
Under these circumstances, the expression defining reservation wage is now:
![]() (4)
(4)
where  refers to the reservation wage in this new setting. Now, the reservation wage would be (minus) the slope of the line
refers to the reservation wage in this new setting. Now, the reservation wage would be (minus) the slope of the line ![]() in Figure 2, where the worker must bear a loss of leisure
in Figure 2, where the worker must bear a loss of leisure ![]() (which will not be remunerated) so as to get a job. Note that the right hand side of (4) is not altered with the changes in
(which will not be remunerated) so as to get a job. Note that the right hand side of (4) is not altered with the changes in![]() . Nevertheless, the left hand side of such expression and the size of the search costs are inversely related:
. Nevertheless, the left hand side of such expression and the size of the search costs are inversely related: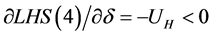 . This implies that the reservation wage must move in the same direction as
. This implies that the reservation wage must move in the same direction as ![]() to re-establish equality in expression (4). From a geometric point of view, it is clear in Figure 2 that an increase of
to re-establish equality in expression (4). From a geometric point of view, it is clear in Figure 2 that an increase of ![]() entails a greater steepness of the line
entails a greater steepness of the line![]() . Therefore, there is a direct relationship between search costs and the reservation wage and an inverse relationship between such costs and labour market participation12.
. Therefore, there is a direct relationship between search costs and the reservation wage and an inverse relationship between such costs and labour market participation12.
The key question is: what are the effects of changes in  on labour force participation in this new theoretical setting? To answer this question, we must follow the same steps as in the previous framework. The right hand side of (4) is not modified when
on labour force participation in this new theoretical setting? To answer this question, we must follow the same steps as in the previous framework. The right hand side of (4) is not modified when  does, whereas alterations in the left hand side can be defined by means of expression (5), but taking into consideration that the
does, whereas alterations in the left hand side can be defined by means of expression (5), but taking into consideration that the ![]() is now assessed in the
is now assessed in the ![]() consumption-leisure pair:
consumption-leisure pair:
 (5)
(5)
It is worth mentioning that, in the current theoretical scenario, the convexity of the indifference curves does
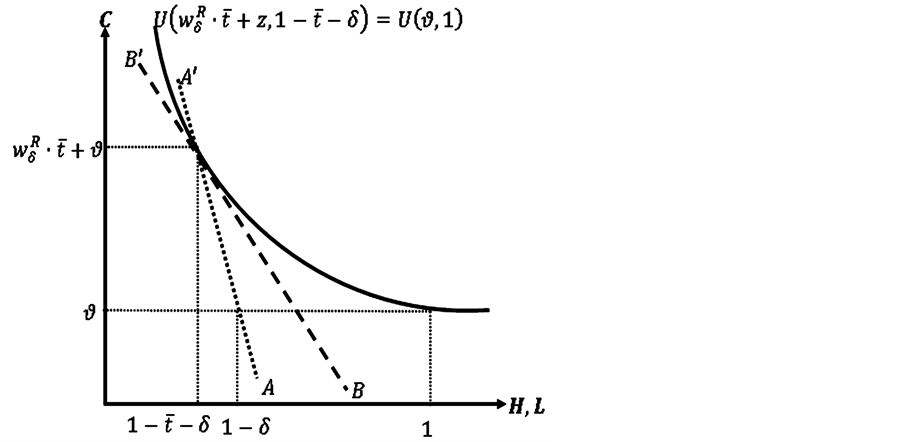
Figure 2. Reservation wage and MRS with transaction costs.
not guarantee that  and (5) is not undoubtedly negative. Therefore, it cannot be taken for granted the existence of an unambiguous inverse relationship between regulated working hours and labour participation. A graphical counter-example showing that is presented in Figure 2. In such a figure, the
and (5) is not undoubtedly negative. Therefore, it cannot be taken for granted the existence of an unambiguous inverse relationship between regulated working hours and labour participation. A graphical counter-example showing that is presented in Figure 2. In such a figure, the ![]() (measured by the slope of the line
(measured by the slope of the line![]() , in absolute value) is lower than the reservation wage (measured by the slope of the line
, in absolute value) is lower than the reservation wage (measured by the slope of the line![]() , with opposite sign). Nonetheless, we have to indicate that Figure 2 only tries to illustrate that the clear relationship obtained in Result 1 is not kept with the assumptions of the present theoretical setting. Let us delve into this issue a little more.
, with opposite sign). Nonetheless, we have to indicate that Figure 2 only tries to illustrate that the clear relationship obtained in Result 1 is not kept with the assumptions of the present theoretical setting. Let us delve into this issue a little more.
We know that if ![]() then we may state unequivocally that
then we may state unequivocally that . We also know that when
. We also know that when ![]() increases, both MRS at the point
increases, both MRS at the point ![]() and
and 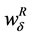 increase. But it is necessary to establish a more precise relationship between the changes in
increase. But it is necessary to establish a more precise relationship between the changes in ![]() and
and  when
when ![]() varies. Applying the implicit function theorem on equation (4) allows us to assess how
varies. Applying the implicit function theorem on equation (4) allows us to assess how 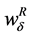 changes when
changes when ![]() varies13:
varies13:
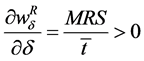 (6)
(6)
On the other hand, we may calculate how ![]() changes by partially deriving it, which produces14 expression (7):
changes by partially deriving it, which produces14 expression (7):
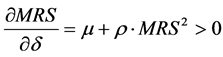 (7)
(7)
where 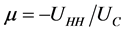 and
and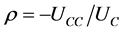 . As it can be seen, the order of magnitude 6 and 7 will depend on the individual’s taste for income or consumption and leisure (labour).
. As it can be seen, the order of magnitude 6 and 7 will depend on the individual’s taste for income or consumption and leisure (labour).
Result 2: When high unemployment makes search transaction costs not negligible, a reduction in regulated working time will not have an unambiguously encouraging effect on labour market participation. The final result will depend on worker’s tastes on income or consumption and leisure (labour).
5. A Numerical Counter-Example
In order to illustrate the Result 2 presented in section 4 and, at the same time, to look into it, in this section we use a specific set of preferences. If we take as a starting point a popular Cobb-Douglas utility function such as:
![]() (8)
(8)
Taking a logarithmic transformation, that is, an increasing monotonic transformation, we obtain:
 (9)
(9)
It is well known that in a world of ordinal utility the functions displayed in expressions (8) and (9) reflect the same set of preferences. Expression (9) is a particular case15 of the more general preference representation considered in Assumption 3. Bearing this utility function in mind, it is easy to assess the expression for the reservation wage. It is shown in Equation (10):
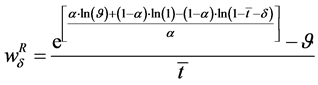 (10)
(10)
On the other hand, it is easy to probe that the utility function shown in (9) produces a ![]() that can be simply written as:
that can be simply written as:
 (11)
(11)
In Figure 3, we depict both ![]() and
and 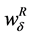 as functions of
as functions of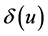 . The parameter values used are the following:
. The parameter values used are the following:![]() ,
, 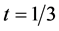 and
and![]() . We may see that, as it was established through expressions (6) and (7), both
. We may see that, as it was established through expressions (6) and (7), both 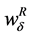 and
and ![]() increase as unemployment rises (and makes
increase as unemployment rises (and makes ![]() rise). Furthermore, the parameterization allows us to gain some additional insights16. When unemployment is low and consequently
rise). Furthermore, the parameterization allows us to gain some additional insights16. When unemployment is low and consequently ![]() is low then
is low then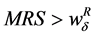 . This would give support to Result 1 in contexts where the levels of unemployment were not very high. However, as unemployment rises, and
. This would give support to Result 1 in contexts where the levels of unemployment were not very high. However, as unemployment rises, and ![]() rises consequently, Result 1 becomes less likely.
rises consequently, Result 1 becomes less likely.
As it may also be observed in Figure 3, firstly 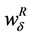 increases faster than
increases faster than ![]() and might equalize it and even exceed it. If it were the case, the basic prediction obtained in Result 1 would reverse. In other terms, a reduction in regulated working time would discourage labour participation instead of encouraging it.
and might equalize it and even exceed it. If it were the case, the basic prediction obtained in Result 1 would reverse. In other terms, a reduction in regulated working time would discourage labour participation instead of encouraging it.
To go into this question, we draw Figure 4. In such a figure, we represent the difference between 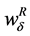 and
and ![]() as a function of
as a function of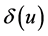 . The reason for doing that is that the difference between
. The reason for doing that is that the difference between 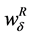 and
and ![]() de-
de-
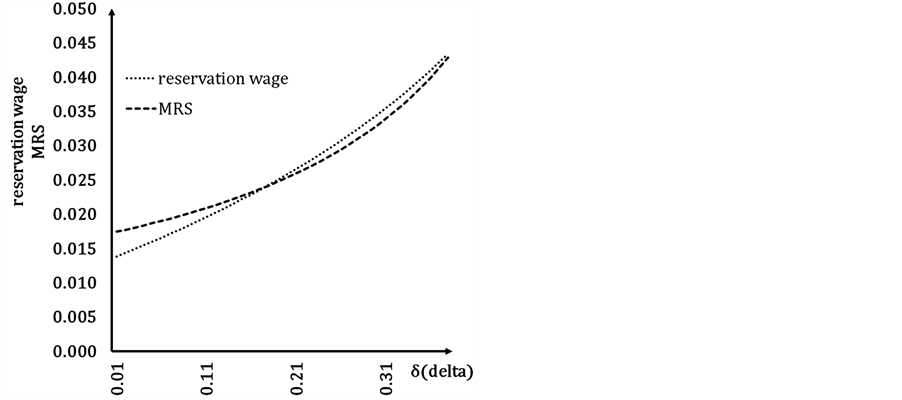
Figure 3. Reservation wage and MRS as a function of delta.

Figure 4. Reservation wage minus MRS as a function of delta.
termines the sign of expression (5) and this, in turn, the final effect over labour participation. Moreover, we consider three alternative values for alpha:![]()
![]() and
and![]() .
.
The main conclusion we obtain from inspection of Figure 4 is that for low levels of unemployment the basic inverse relation between regulated working time and labour participation prevails. As the unemployment levels increases, there is a greater likelihood of finding a direct relation between both variables, that is, a reduction of regulated working time would provoke a reduction in labour participation. Finally, for enough high levels of unemployment the basic relation could appear again. This takes us to Result 3:
Result 3: As unemployment rises the likelihood of an encouraging effect on labour participation of a reduction in regulated working time decreases until certain point. From this point onwards the basic relationship appears again.
6. Concluding Remarks
In this paper, a clear conclusion has been achieved: we have shown that the basic relationship between a reduction in regulated working time and an increase in labour market participation is far from being evident in a model with search transaction costs. Moreover, we have also reached a set of derived results.
Firstly, from a theoretical point of view, we have obtained that as unemployment goes up, the likelihood of finding a decrease in labour force participation following a reduction in regulated working time increases as well. At the same time, another appealing feature is that such a relationship is not monotonic, that is, there could be a turning point from which the usual relationship involving working time reductions and labour force participation would appear again.
Secondly, from an empirical perspective, an obvious research work that could be performed is to test if the effect identified here is relevant both at the individual and the aggregate level. By using microdata, it could be feasible to check the role of worker’s tastes on income or consumption and leisure (labour) and of the other variables, especially the role of non-labour income. At the macro level, the interest would be in assessing what level of unemployment rate would change the basic relationship between a decrease in regulated hours and the participation rate (if that happened) and what unemployment rate would revert the situation (if it were the case).
Finally, adopting an economic policy standpoint, the above mentioned result possesses some remarkable implications. As it has already been pointed out, it is when unemployment is high politicians are more concerned with work-sharing measures. At least, that what recent history tells us. At the same time, as long as unemployment rises, search transaction costs increase and the likelihood of conventional wisdom exposed in Result 1 being true diminishes (at least up to certain point). This would entail that a decrease in regulated working time in high unemployment contexts could be associated with a reduction in labour force participation instead with an increase of it, and this would happen precisely when more likely is to take those political measures.
References
- Kramarz, F., Cahuc, P., Crepon, B., Schank, T., Skans, O.N., van Lomwel, G. and Zylberberg, A. (2008) Labour Market Effects of Work-Sharing Arrangements in Europe. In: Boeri, T. Burda, M. and Kramarz, F., Eds., Working Hour and Job Sharing in the EU and the USA: Are Europeans Lazy or Americans Crazy? Oxford University Press, Oxford.
- Viscusi, W.K., Harrington J.E. and Vernon, J.M. (2005) Economics of Regulation and Antitrust. 4th Edition, The MIT Press, Cambridge.
- Boeri, T. (2008) Understanding Transatlantic Differences in Working Hours. In: Boeri, T., Burda, M. and Kramarz, F., Eds., Working Hour and Job Sharing in the EU and the USA: Are Europeans Lazy or Americans Crazy? Oxford University Press, Oxford, 1-9.
- Hart, R.A. and Sharot, T. (1978) The Short-Run Demand for Workers and Hours: A Recursive Model. Review of Economic Studies, 45, 299-309. http://dx.doi.org/10.2307/2297345
- Bell, D. (1982) Labour Utilization and Statutory Non-Wage Cost. Economica, 49, 335-343. http://dx.doi.org/10.2307/2553633
- Hart, R.A. (1984) Worksharing and Factor Prices. European Economic Review, 24, 165-188. http://dx.doi.org/10.1016/0014-2921(84)90105-3
- Hoel, M. and Vale, B. (1986) Effects on Unemployment of Reduced Working Time in a Economy Where Firms Set Wages. European Economic Review, 30, 1097-1104. http://dx.doi.org/10.1016/s0014-2921(86)80008-3
- Leslie, D. (1987) Motivating Wage Structures. European Economic Review, 31, 1267-1283. http://dx.doi.org/10.1016/s0014-2921(87)80017-x
- Leslie, D. (1991) Modelling Hours of Work in a Labour Services Function. Scottish Journal of Political Economy, 38, 19-31. http://dx.doi.org/10.1111/j.1467-9485.1991.tb00298.x
- Calmfors, L. and Hoel, M. (1988) Worksharing and Overtime. Scandinavian Journal of Economics, 90, 45-62. http://dx.doi.org/10.2307/3440149
- Calmfors, L. and Hoel, M. (1989) Worksharing, Employment and Shift Work. Oxford Economic Papers, 41, 758-773.
- König, H. and Pohlmeier, W. (1989) Worksharing and Factor Prices: A Comparison of Three Flexible Functional Forms for Nonlinear Cost Schemes. Journal of Institutional and Theoretical Economics, 145, 343-357.
- Contensou, F. and Vranceanu, R. (1998) A Model of Working Time under Utility Competition in the Labor Market. Journal of Economics, 67, 145-166. http://dx.doi.org/10.1007/bf01236067
- Marimon, R. and Zilibotti, F. (2000) Employment and Distributional Effects of Restricting Working Time. European Economic Review, 44, 1291-1326. http://dx.doi.org/10.1016/s0014-2921(00)00032-5
- Rocheteau, G. (2002) Working Time Regulation in a Search Economy with Worker Moral Hazard. Journal of Public Economics, 84, 387-425. http://dx.doi.org/10.1016/s0047-2727(01)00087-1
- Askenazy, P. (2004) Shorter Work Time, Hours Flexibility, and Labor Intensification. Eastern Economic Journal, 30, 603-614.
- Hunt, J. (1998) Hours Reduction as Work-Sharing. Brookings Papers on Economic Activity, 1998, 339-369. http://dx.doi.org/10.2307/2534674
- Hunt, J. (1999) Has Work-Sharing Worked in Germany? Quarterly Journal of Economics, 114, 117-148. http://dx.doi.org/10.1162/003355399555963
- Crépon, C. and Kramarz, F. (2002) Employed 40 Hours or Not Employed 39: Lessons from the 1982 Mandatory Reduction of the Workweek. Journal of Political Economy, 110, 1355-1389. http://dx.doi.org/10.1086/342807
- Kapteyn, A., Kalwij, A. and Zaidi, A. (2004) The Myth of Worksharing. Labour Economics, 11, 293-313. http://dx.doi.org/10.1016/j.labeco.2003.08.001
- Boeri, T. and Bruecker, H. (2011) Short-Time Work Benefits Revisited: Some Lessons from the Great Recession. Economic Policy, 26, 697-765. http://dx.doi.org/10.1111/j.1468-0327.2011.271.x
- Burda, M.C. and Hunt, J. (2011) What Explains the German Labor Market Miracle in the Great Recession? Brookings Papers on Economic Activity, 42, 273-335. http://dx.doi.org/10.1353/eca.2011.0004
- Calmfors, L. (1985) Worksharing, Employment and Wages. European Economic Review, 27, 293-309. http://dx.doi.org/10.1016/S0014-2921(85)80017-9
- Hoel, M. (1986) Employment and Allocation Effects of Reducing the Length of the Workday. Economica, 53, 75-85. http://dx.doi.org/10.2307/2554521
- Booth, A. and Schiantarelli, F. (1987) The Employment Effects of a Shorter Working Week. Economica, 54, 237-248. http://dx.doi.org/10.2307/2554393
- Booth, A. and Ravallion, M. (1993) Employment and Length of the Working Week in a Unionized Economy in Which Hours of Work Influence Productivity. Economic Record, 69, 428-436. http://dx.doi.org/10.1111/j.1475-4932.1993.tb02124.x
- Pérez-Domínguez, C. (2002) Effects of a Reduction of Standard Working Hours on Labour Market Performance. In: Coto-Millán, P., Ed., Essays in Microeconomics and Industrial Organization, Springer, Berlin, 167-182. http://dx.doi.org/10.1007/978-3-662-11710-1_12
- Cahuc, P. and Zylberberg, A. (2004) Labor Economics. MIT Press, Cambridge.
- Boeri, T. and van Ours, J. (2008) The Economics of Imperfect Labor Markets. Princeton University Press, Princeton.
- Zabalza, A., Pissarides, C. and Barton, M. (1980) Social Security and the Choice between Full-Time Work, Part-Time Work and Retirement. Journal of Public Economics, 14, 245-276. http://dx.doi.org/10.1016/0047-2727(80)90042-0
NOTES

1A revealing example is the case in Spain during the year 2008. According to the Survey of Active Population, the number of unemployed people in the fourth quarter of the year 2007 was 1,927,600 and a year later this figure was 3,207,900. So, the number on unemployed workers went up by 1,280,300. But the interesting thing is how this huge increase in unemployment is explained: while the employed people decreased by 620,100, at the same time the labor force increased by 660,200 people.

2We may think of the week as being the time framework relevant to take decisions by the individuals. Nonetheless our theoretical approach is more general than that.
3More recently, different approaches have been taken into consideration in order to deal with this issue. Some examples of this “new economics of work-sharing” are Contensou and Vranceanu , Marimon and Zilibotti , Rocheteau or Askenazy . In any case, these approaches are out of the scope of this paper.
4Without the aim of being exhaustive we could also cite Kapteyn et al. and Kramarz et al. .

5The theoretical framework developed in this section coincides to a great extent with those models that can be found in Pérez-Domínguez and Boeri and vans Ours . Nonetheless, our presentation of the results differs from them in order to better understand the next section.
6We are interested in what Kramartz et al. call “pure” effects of working time reductions. For this reason we will suppose that wage per time unit remains constant from now onwards.
7We can suppose that standard working hours have been established by means of a procedure of collective bargaining or through a decree, an act, a directive or a law.
8Some examples of discrete possibility sets can be found in the works of Zabalza et al. and Perez-Dominguez .
9Which simplifies the algebra and allow us to focus on the participation decision, leaving aside the question of the number of hours supplied.
10Assuming an additive utility function is a sufficient condition (but not necessary) to get some of the results included in this paper.
11It is well known that these types of utility functions generate convex indifference curves.

12The inverse relationship between time costs and participation is well-known within labour economics.

13From (4) we can define the following implicit function: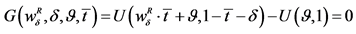 . From the previous expression it is easy to compute:
. From the previous expression it is easy to compute:
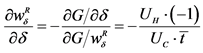
Arranging the above equation gives expression (6) in the text.
14The partial derivative of 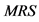 with respect to
with respect to  can be written in the following manner:
can be written in the following manner:
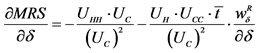
By manipulating the terms, and by using expression (6) we obtain expression (7).
15We implicitly are supposing that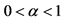 .
.

16It is quite evident that the precise results are quantitatively sensitive to the values of the parameters. However, the aim of this section is simply to provide a counter-example and to show a general principle. In any case, other simulations are available from the author upon request.

