Theoretical Economics Letters
Vol.3 No.2(2013), Article ID:30584,5 pages DOI:10.4236/tel.2013.32014
Hardy-Weinberg Equilibrium and Mixed Strategy Equilibrium in Game Theory
Faculty of Business Administration, Hosei University, Tokyo, Japan
Email: horaguch@hosei.ac.jp
Copyright © 2013 Haruo H. Horaguchi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 4, 2013; revised March 3, 2013; accepted April 2, 2013
Keywords: Hardy-Weinberg Equilibrium; Nash Equilibrium; Mixed Strategy; Mendelian Proportions
ABSTRACT
The Hardy-Weinberg Equilibrium (HWE) can be linked to game theory. This article shows that payoffs, or resources, in a game with alleles as players, determine the frequency of homozygotes. The frequency of aa homozygotes in the HWE is an increasing function of the multiplicative difference in own payoffs for each allele. Thus, Mendelian proportions are variable rather than fixed depending on the resources for the alleles. Whereas the concept of evolutionary stable strategy (ESS) is based on non-cooperative competitive settings such as a competition between doves and hawks, this article explores a game theoretic situation where the mating of two alleles is presupposed.
1. Introduction
There is an equilibrium concept that is not used by game theorists or by economists but exclusively used by biologists. The Hardy-Weinberg Equilibrium (HWE) is the name of this equilibrium concept [1]. The HWE explains Mendelian proportions from theoretical calculation of the allele frequencies [2,3]. This article shows that the HWE can be linked to game theory so that game theorists and economists can reinterpret the HWE through the lens of game theory.
Maynard Smith proposed the concept of evolutionary stable strategy (ESS) which was based on non-cooperative competitive settings such as competition between doves and hawks [4]. This article explores a situation where the mating of two alleles is presupposed. This is considered as one of cooperative games even though two alleles are influenced by the payoff structure. A basic notion of mixed strategy equilibrium in game theory [5-8] is applied to reinterpret the HWE.
This article reveals that payoffs for alleles, or resources for players, determine the frequency of homozygotes. The main result of this article suggests that Mendelian proportions are variable rather than fixed depending on the resources for the alleles encountered. Although this result may not influence the academic interests of biologists because the author is not capable of reviewing the existing literature in biology, the introduction of a new equilibrium concept to the field of game theory may well develop yet unknown field of research as applications of the HWE.
An example to apply this approach in economic phenomenon is to investigate diffusion of solar panels on household roofs. We can observe a fraction of cases where a wife and a husband agree to install the solar panel. The wife and the husband have options to choose either to consume fossil energy or to install solar panels. The resources or the payoffs in this game are influenced in various ways such as a subsidy for installing solar panels, the budgets of the husband and wife, the amount of daytime sun in the region and an electric power company scheme to buy surplus electricity from the household. The couple pursues an eco-friendly life when there are large enough payoffs for their installation. Measurement of these variables in actual data is left for empirical research, however.
Section 1 shows the basic logic of the HWE. Section 2 explains how to find a mixed strategy Nash equilibrium given payoffs, or resources to be utilized by each allele. Section 3 shows that the frequency of aa homozygotes in the HWE is an increasing function of the multiplicative difference in own payoffs for each allele. Section 4 discusses how we can apply the HWE notion to the third and fourth generations with different frequencies in alleles. A model in this section shows that mathematical structure of the HWE converges on the structure in the Wiener process. The concluding section sums up the major propositions.
2. The HWE with General Probability
2.1. Basic Model
Suppose there are two alleles: the first allele is denoted A and the second is denoted a [9]. Their frequencies are denoted by p and q resectively;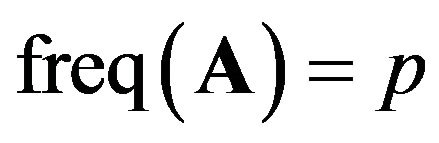 ;
;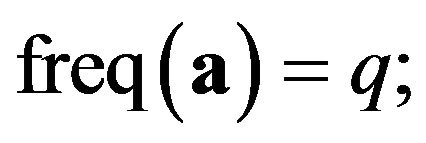
 . If mating is random, then new individuals will have
. If mating is random, then new individuals will have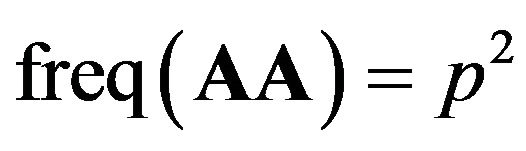 . AA is called homozygotes in the population and aa for
. AA is called homozygotes in the population and aa for 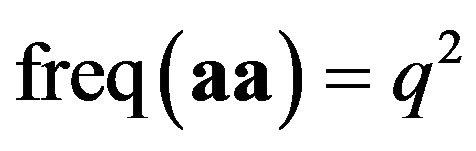 is called “aa homozygotes”. And Aa for
is called “aa homozygotes”. And Aa for 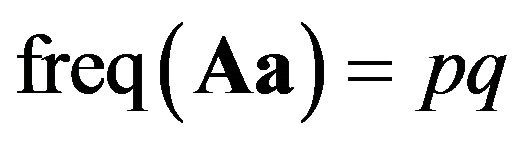 or aA for
or aA for  is called hetrozygotes. Given that there is random mating, we call the two parties male and female in Table 1.
is called hetrozygotes. Given that there is random mating, we call the two parties male and female in Table 1.
2.2. Extension of the Specifications
The ratio of the homozygotes to the hetrozygotes given in the above example is p2:2pq:q2. This result is derived only when males and females have the same ratio of two alleles in their frequencies p and q. Now, suppose males and females have different frequencies to create homozygotes and heterozygotes. Suppose further that males have the ratio of p and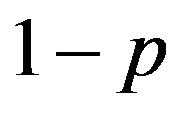 , and females have the frequency ratio of q and
, and females have the frequency ratio of q and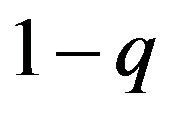 . As shown in Table 2, the ratio of the homozygotes to the hetrozygotes is;
. As shown in Table 2, the ratio of the homozygotes to the hetrozygotes is; . The HWE in a biology textbook [10] begins with a special case where p = q. Although this generalization seems to be a trivial change in the HWE model, we are now able to connect the HWE to game theory.
. The HWE in a biology textbook [10] begins with a special case where p = q. Although this generalization seems to be a trivial change in the HWE model, we are now able to connect the HWE to game theory.
3. The HWE and Game Theory
3.1. Nash Equilibrium
Table 3 shows an example of payoffs. Table 3 has three
Table 1. Homozygotes and hetrozygotesa.

aSee for example [10], p. 41.
Table 2. Unique probability for mating.

Table 3. Payoff matrix.

Nash equilibria: two of pure strategy and one of a mixed strategy. The equilibrium in the pure strategy is a combination of (Growth strategy, Eco strategy) and (Ecostrategy, Growth strategy). These equilibriums satisfy the definition of Nash equilibrium where a best response of a player coincides with another player’s best response.
I can calculate the Nash equilibrium in the mixed strategy using the probability given in Table 3. The expected payoffs for the player one, or the males is;

We see the following relationships.
If 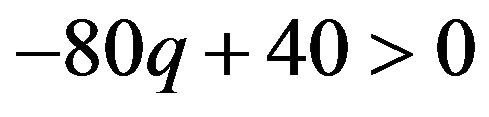 then
then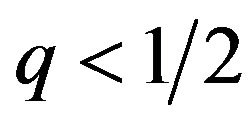 , or
, or .
.
If  then
then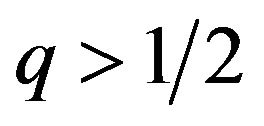 , or
, or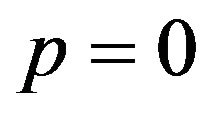 .
.
If 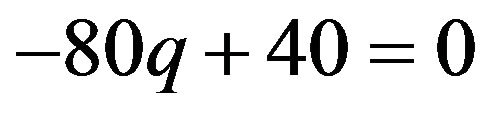 then
then , or
, or .
.
The best responses for the male group strategy are shown the above. If the coefficient parameter of p, which is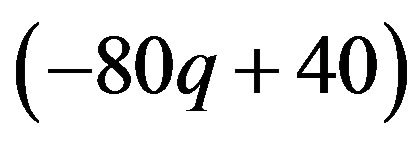 , is positive, it is equivalent to the probability q of the strategic choice of the females which is smaller than
, is positive, it is equivalent to the probability q of the strategic choice of the females which is smaller than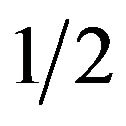 . The male group can maximize own expected payoffs by maximizing p in this situation. Therefore, the best response of the male group is to take a pure strategy of
. The male group can maximize own expected payoffs by maximizing p in this situation. Therefore, the best response of the male group is to take a pure strategy of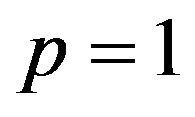 . If the coefficient parameter
. If the coefficient parameter  is negative, probability q is larger than
is negative, probability q is larger than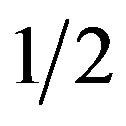 . For the male group, the best response is to take strategy of
. For the male group, the best response is to take strategy of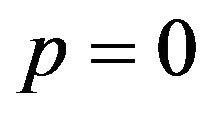 . This means that minimizing p leads to maximization of males expected payoffs. When the coefficient parameter
. This means that minimizing p leads to maximization of males expected payoffs. When the coefficient parameter 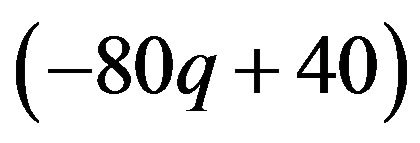 is 0, which indicates
is 0, which indicates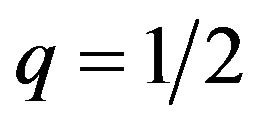 , then the expected payoffs for the male group does not depend on p.
, then the expected payoffs for the male group does not depend on p.
Expected payoffs for females are;

We see the following relationships:
If 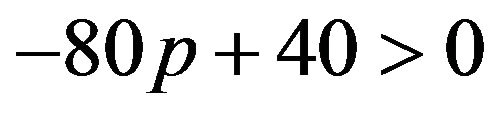 then
then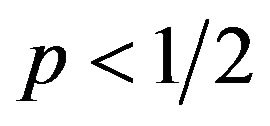 , or
, or .
.
If 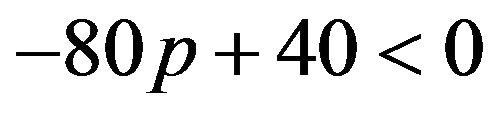 then
then , or
, or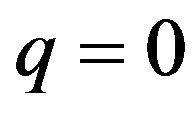 .
.
If  then
then , or
, or .
.
From the above the best responses for the female group are as follows: when , it is equivalent to
, it is equivalent to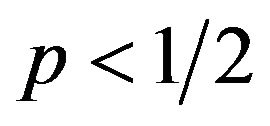 . The female can maximize q to get the highest amount of payoffs. The maximum of q is 1.
. The female can maximize q to get the highest amount of payoffs. The maximum of q is 1.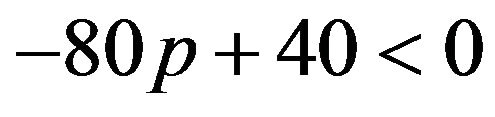 , or when probability
, or when probability , q must be minimized to get the highest payoffs for the female. The minimum is zero. These two cases correspond to pure strategies. If
, q must be minimized to get the highest payoffs for the female. The minimum is zero. These two cases correspond to pure strategies. If 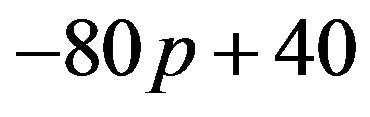 is equal to zero, then
is equal to zero, then . This means that the expected payoff for females is
. This means that the expected payoff for females is , which does not depend on q.
, which does not depend on q.
Thus, two pure strategies are derived. One is that females choose the Eco-strategy when the males choose the Growth strategy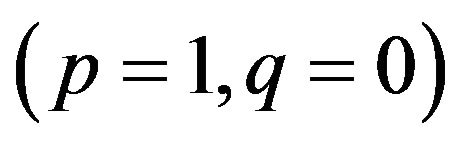 . The other is the combination that the females choose the Growth Strategy when the male group chooses the Eco-strategy (p = 0, q = 0). The Nash equilibrium for the mixed strategy is also apparent. The male group assigns the probability of
. The other is the combination that the females choose the Growth Strategy when the male group chooses the Eco-strategy (p = 0, q = 0). The Nash equilibrium for the mixed strategy is also apparent. The male group assigns the probability of 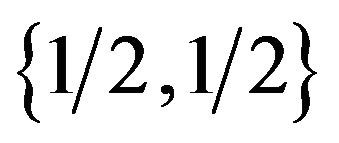 to p and
to p and 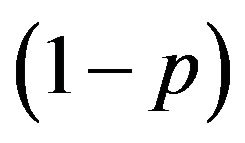 for its {Growth strategy, Eco-strategy}, and the females allocate the combinations of the best response to give
for its {Growth strategy, Eco-strategy}, and the females allocate the combinations of the best response to give 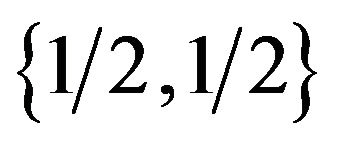 to q and
to q and 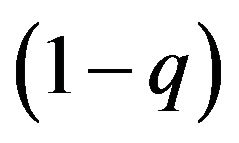 for its {Growth strategy, Eco-strategy}. We can show these results as two reaction functions in Figure 1.
for its {Growth strategy, Eco-strategy}. We can show these results as two reaction functions in Figure 1.
Calculating the expected payoffs under this mixed strategy gives
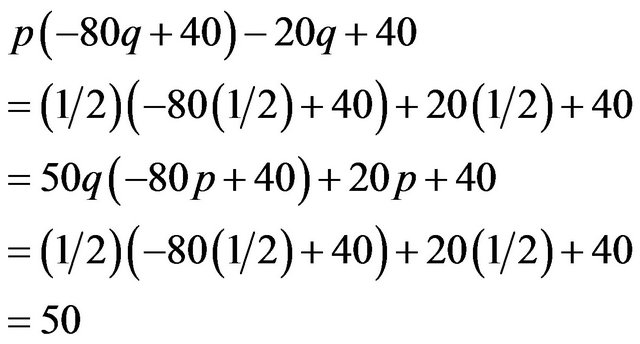
The males and the females obtain payoffs of (50, 50) respectively under the mixed strategy Nash equilibrium. Here we can also get . Consequently,
. Consequently, 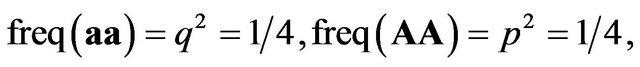 and
and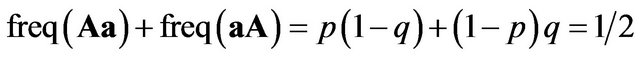 .
.
What is more important in relation to the HWE is that the frequency of p and q is simultaneously determined by the existing conditions of the payoffs for the mixed strategy. When biologists calculate the HWE, they observe the aa homozygotes which is supposed to be given by 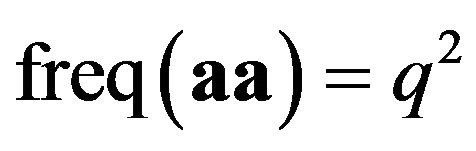 in Table 1. One can see that
in Table 1. One can see that
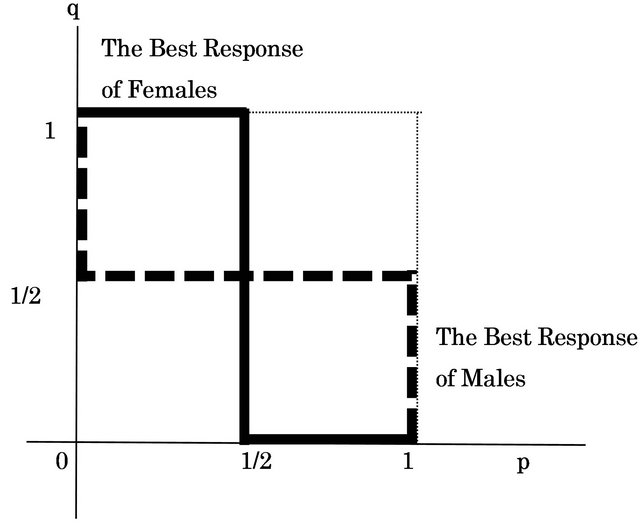
Figure 1. Reaction functions of males and females.
 is equivalent to
is equivalent to 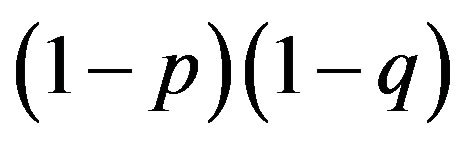 in our example of Table 2, which is derived from the payoff matrix in Table 3. Eight payoffs in Table 3 collectively decide p and q. Mendelian proportions are not inherited but are determined by payoffs, or resources, for the alleles.
in our example of Table 2, which is derived from the payoff matrix in Table 3. Eight payoffs in Table 3 collectively decide p and q. Mendelian proportions are not inherited but are determined by payoffs, or resources, for the alleles.
Proposition 1. The frequency of the aa homozygotes in the HWE is a function of payoffs in a game for two alleles.
I must emphasize that the symmetrical payoffs in Table 3 are not essential. I can easily show that there is a mixed strategy Nash equilibrium in the case where there is no pure strategy Nash equilibrium. What I can observe in Mendelian proportions is  as the frequency of the aa homozygotes and I can infer the existence of a game behind it. The generalization of obtaining a mixed strategy Nash equilibrium is considered in the next section.
as the frequency of the aa homozygotes and I can infer the existence of a game behind it. The generalization of obtaining a mixed strategy Nash equilibrium is considered in the next section.
3.2. General Model with Parameters
There are eight payoffs in the game, or four payoffs for each allele. We allocate eight parameters as a payoff matrix: . Let us start from the males’ case where we give four parameters, a, b, c and d as payoffs for the males.
. Let us start from the males’ case where we give four parameters, a, b, c and d as payoffs for the males.
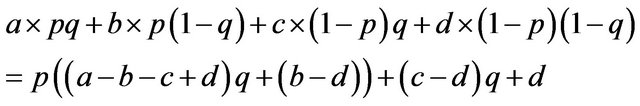
If 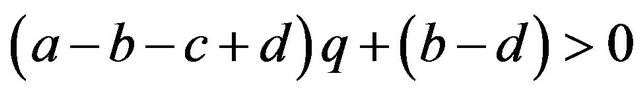
then , or
, or .
.
If 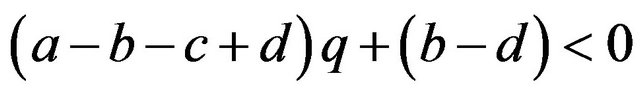
then , or
, or .
.
If 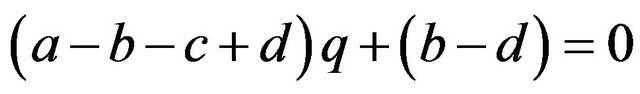
then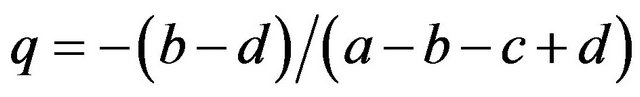 , or
, or .
.
We give parameters e, f, g and h for the payoffs for the females’ case;

If 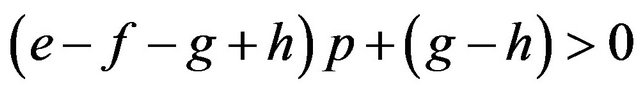
then , or
, or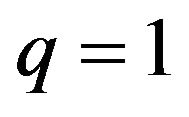 .
.
If 
then , or
, or .
.
If 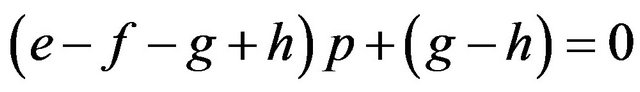
then , or
, or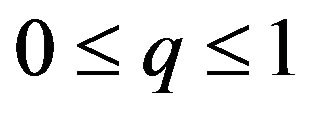 .
.
We can calculate p and q given these parameters. Accordingly we can calculate the expected payoffs of the mixed strategies. The males obtain;
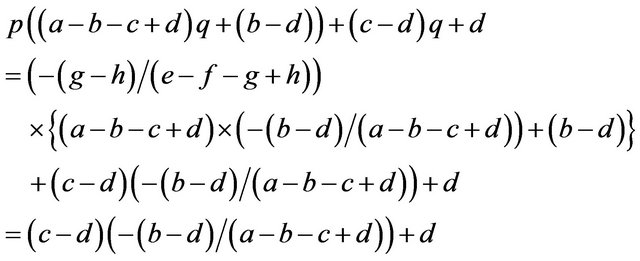
and the females obtain their payoffs;

These results give paradoxical characteristics of mixed strategy.
Proposition 2. Payoffs attained by the mixed strategy for each of the two players do not depend on the other player’s payoffs in the game.
3.3. The HWE Reconsidered
We obtained in the former section that:
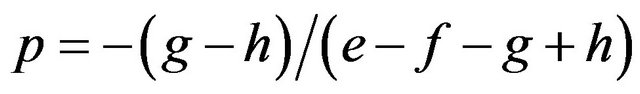
and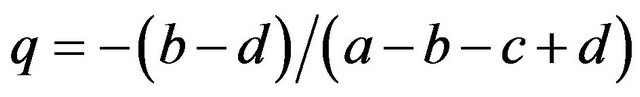 .
.
Let us denote 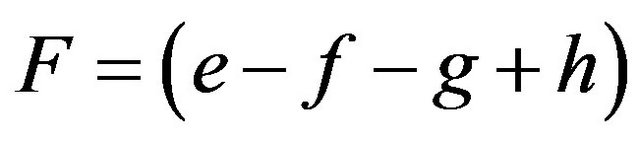 and
and .
.
Then we get;

As shown in Proposition 1, the HWE is dependent on the payoff matrix of the game.
When biologists start off by observing the frequency of the aa homozygotes, which is supposed to be given by , they are looking at
, they are looking at  or
or
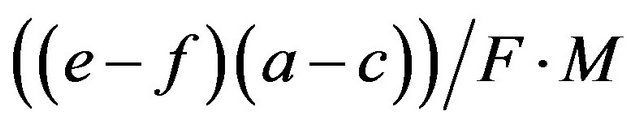 in our exposition. I see the possibility that payoff e is closer to f and/or payoff a is closer to c. In such cases the multiplication of
in our exposition. I see the possibility that payoff e is closer to f and/or payoff a is closer to c. In such cases the multiplication of  and
and  approaches to zero. If both results are closer, then
approaches to zero. If both results are closer, then  converges to zero at an accelerated pace. If, on the other hand, the difference between the two payoffs increases such that e and f and/or a and c have wider gaps in their payoff levels, then the frequency expressed by
converges to zero at an accelerated pace. If, on the other hand, the difference between the two payoffs increases such that e and f and/or a and c have wider gaps in their payoff levels, then the frequency expressed by 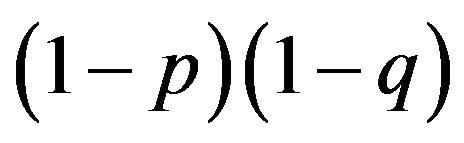 increases.
increases.
Proposition 3. The frequency of the aa homozygotes in the HWE is an increasing function of the multiplicative difference in own payoffs  for each allele given
for each allele given  and
and
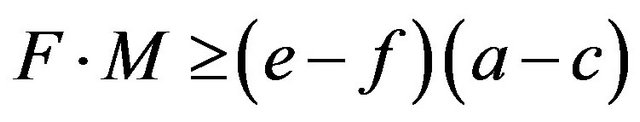 .
.
4. Analysis and Discussion: The Third and the Fourth Generation
In this article the HWE has been explained through the logic of the game theoretic optimal behavior of alleles. However, questions remain as to how we understand the third and fourth generations that have different frequencies of alleles. One of the expositions of showing the aa homozygotes is shown in Figure 2. The upper line of the tree shows an addition of the first allele A and the lower line shows the addition of the second allele a. The HWE is derived from the observance of the aa homozygotes.
The question is how one can find aa homozygotes in the third generation. I see that there are two ways to obtain the HWE in the third generation from Figure 2. The first case is to get the aa homozygotes from the top two sequences of aa. These cases are shown underlined in Figure 2. In this case, the third generation directly inherits the aa homozygotes from the second generation. The second case is to get the aa homozygotes from the last two sequence for aa, which are depicted by rectangles in Figure 2. We can also get the one-fourth of the frequency for the aa homozygotes among the total population. Both of the cases retain the same ratio of one-fourth in the case of the fourth generation.
The sequence is important because frequencies may differ between generations. If we assume that the top two sequences of alleles define the aa homozygotes, the fourth generation with aa homozygotes is directly inherited from the third generation. This frequency is one
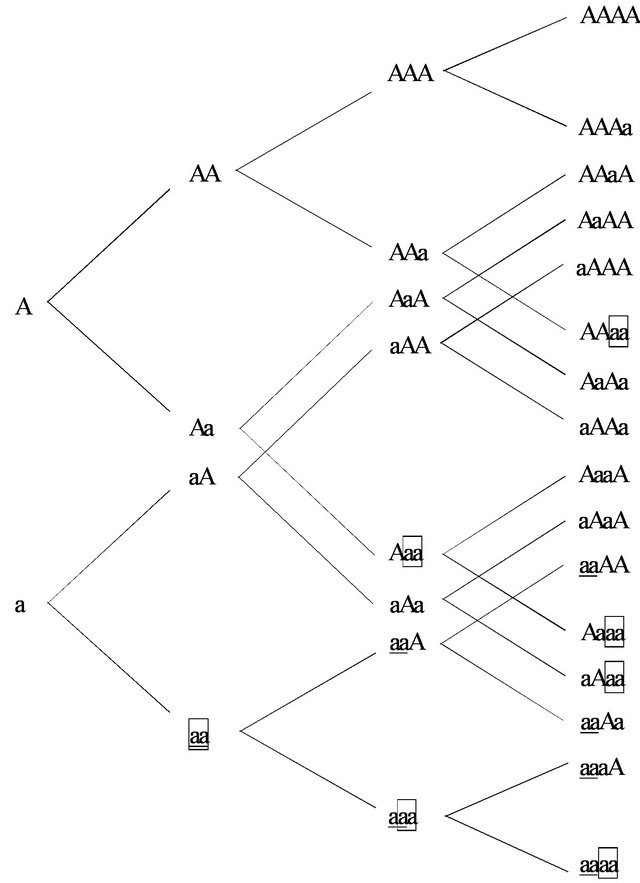
Figure 2. Extensive form of allele sequence.
hundred percent. If the last two sequences of allele define the aa homozygotes, one half of the parental generation for the fourth generation is aa homozygotes. In the case of the top two sequences, the fourth generation shows aaAA, aaAa, aaaA and aaaa. If we check the third generation, we get aaA and aaa as the ancestors. In the case of the last two sequences, we see those cases at AAaa, Aaaa, aAaa and aaaa. The third generation for them consists of AAa, Aaa, aAa and aaa. The third generation comes from a wider range for the hetrozygotes.
We are now able to allocate the probabilities in any generations. We see that the probability of AA is pq, of Aa is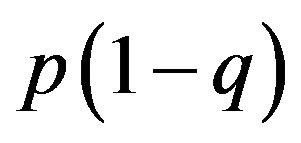 , of aA is
, of aA is  and of aa is
and of aa is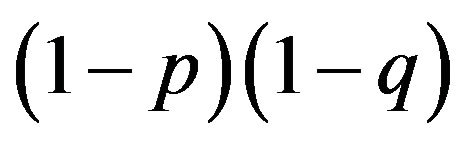 . We can also calculate from Figure 2 the probabilities that are allocated in the third and fourth generations.
. We can also calculate from Figure 2 the probabilities that are allocated in the third and fourth generations.
The probability distribution in Figure 2 shows a binomial distribution. Thus we see that the mathematical structure of Figure 2 is the same as the structure in the Wiener process. Once this approach of showing the extensive form of alleles is admitted to the Wiener process, then dynamic models of real options theory in economics can be applied in conjunction with the HWE and its empirical evidences.
5. Conclusions
Combining the HWE with game theory produced interesting propositions. The frequency of aa homozygotes in the HWE is a function of payoffs in a game for two alleles. And the frequency of aa homozygotes in the HWE is an increasing function of the multiplicative difference in own payoffs for each allele. Therefore I can conclude that Mendelian proportions are variable depending on the resources or the payoffs for the alleles.
It is interesting to inquire how an evolutionary biologist discerns aa homozygotes from mutation when the frequency is so low that aa homozygotes could not appear over many generations. I can further inquire what is conceived if the resources for the alleles fluctuate, increasing after a rare emergence of the aa homozygotes so that their frequency overwhelms that of the heterozygotes and AA homozygotes. These processes seem to be similar to the emergence of mutations and the selection process of species.
6. Acknowledgements
This work was supported by the Japan Society for the Promotion of Science (JSPS), Kakenhi, Grant-in-Aid for Scientific Research (A), 22243032. I am grateful to Professor Marie Anchordoguy at the University of Washington for her academic assistance in my research.
REFERENCES
- G. H. Hardy, “Mendelian Proportions in a Mixed Population,” Science, Vol. 28, No. 706, 1908, pp. 49-50. doi:10.1126/science.28.706.49
- C. Stern, “The Hardy-Weinberg Law,” Science, Vol. 97, No. 2510, 1943, pp. 137-138. doi:10.1126/science.97.2510.137
- C. Stern, “Mendel and Human Genetics,” Proceedings of the American Philosophical Society, Vol. 109, No. 4, 1965, pp. 216-226.
- J. M. Smith, “Evolution and the Theory of Games,” Cambridge University Press, Cambridge, 1982. doi:10.1017/CBO9780511806292
- D. Fudenberg and J. Tirole, “Game Theory,” MIT Press, Cambridge, 1991.
- R. Gibbons, “Game Theory for Applied Economics,” Princeton University Press, Princeton, 1992.
- H. H. Horaguchi, “The Role of Information Processing Cost as the Foundation of Bounded Rationality in Game Theory,” Economics Letters, Vol. 51, No. 3, 1996, pp. 287-294. doi:10.1016/0165-1765(96)00828-2
- D. M. Kreps, “A Course in Microeconomic Theory,” Princeton University Press, Princeton, 1990.
- K. H. Weiss, and J. A. Kurland, “Going on an Antedate: A Strange History of Imperfect Perfect Proportions,” Evolutionary Anthropology, Vol. 16, No. 6, 2007, pp. 204- 209. doi:10.1002/evan.20151
- J. Relethford, “Human Population Genetics,” WileyBlackwell, Hoboken, 2012.

