ABSTRACT

The purpose of this paper is to study on-line portfolio selection strategies for currency exchange markets and our focus is on the markets with presence of decrements. To this end, we first analyze the main factors arising in the decrements. Then we develop a cross rate scheme which enables us to establish an on-line portfolio selection strategy for the currency exchange markets with presence of decrements. Finally, we prove the universality of our on-line portfolio selections.

Keywords:

Currency Markets with Decrements, Cross Rate Method, On-Line Portfolio Selection Strategy, Active Portfolio Management

1. Introduction

We are concerned with a currency exchange market in the presence of decrements. Our objective is to develop an on-line portfolio selection strategy for such a market. To this end, we utilise a cross rate method to establish a suitable algorithm scheme.

The problem of establishing on-line portfolio selection schemes for various financial markets has been well studied (see, e.g. the monograph [1] and a recent paper by Albeverio, Lao, and Zhao [2] , and references therein). We would like in particular to mention [3] and [4] wherein the authors discussed thoroughly the on-line portfolio selection schemes without transaction costs, and [2] addressed the issue with the transaction costs and universality of on-line portfolio selections, following the investi- gation carried out in [5] - [8] .

The on-line portfolio selections can be identified as active portfolio strategies (see, e.g., [2] ). Here an active portfolio means that the currencies to be traded have high price volatility. There are a number of volatility factors affecting the portfolio performance. In the present paper, we introduce four fundamental factors, namely, we will discuss the portfolio performance with presence of: 1) the interest rate; 2) the inflation rate; 3) the income level; and 4) the taxation. We shall take these four elements formulating the term of decrements and then we maximise the profit of the concerned portfolios.

Our consideration follows preliminarily the work of [2] . However, there is a streak difference that in [2] the authors considered two update rules for on-line portfolio selections with transaction costs, while in this paper we will discuss the two update rules for on-line portfolio selections for the currency market with decrements consisting of the above mentioned four factors which lead to certain reduction from the market fluctuates or from the profits of the portfolios.

The paper is organised as follows. Section 2, the next section, starts with the mathe- matical framework setting for the currency exchange market with decrements. Then we introduce two kinds of exponential growth rates. We explicate the occurrence of decrements at the business day 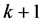from the previous day k and define the distance between the involved portfolio vectors 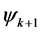and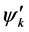. In Section 3, we introduce two update rules in terms of the selection of two different forms of the investment increments and further the formulation of decrements. Then we show how to short the distance by using relative entropy. In the real currency exchange market, the two updates rules turn out to be powerful tools for investors, utilising to make right decisions. In Section 4, we introduce a new prediction method, the so called Cross Rate (CR) method, which emphasises the order of the returns of investment for each currency considered. We present our procedure for taking into account two currencies to demonstrate the CR method: to estimate the cross rate, to predict the order of the return of currencies in the day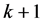, and to get the prediction of the return of currency vector. We follow the feature that higher cross rate indicates that more trading will take place. Section 5 consists two parts. The first part shows that the investors have at least half chance to obtain profitable portfolio in terms of two update rules with the cross rate method, and in the second part we briefly discuss the universality of the two update rules. We end the paper with a conclusion.

2. Preliminaries

2.1. Currency Market Set-Up

The currency market we are concerned is described as follows. Let 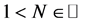be an arbitrarily given nature number. We consider a N period investment in a currency market with time from the initial date, Day one, say, to the terminal date Day N.

・ We assume that the currency exchange market contains m different currencies, where 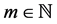is fixed.

・ We suppose that currencies in the market can be perfectly divisible and that at the 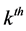day the closing price of currency is equals to the opening price of the day 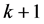(the next day).

・ For 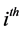currency in the market at the day k, the ratio of the opening price over the closing price of 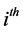currency is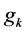, which represents the return on the 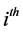currency, at the day k.

・ We denote the vector of the return of m currencies at the 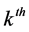trading day by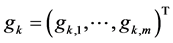, , 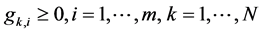where T stands for the trans- pose of a matrix. In certain literature, the return vector is also referred as a price relative (see e.g. [2] ).

・ A portfolio vector 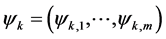represents the invest components in each m currencies at the beginning of the 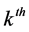day. We denote

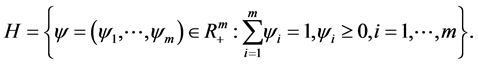(1)

・ The return of the portfolio on the day is defined

(2)

・ The decrement factors which will be specified in the next subsection, namely, we set

(3)

where, and stand for inflation rate, interest rate, income level, and taxation, respectively, and and . is called decrement at the beginning of the day. Since the inflation rate has negative correlation with the other three elements, the should have negative efficiency, while the others have positive efficiency. However, in this case the inflation rate can have positive correlation with decrements. The decrements in our case represents any cost occurs during the trading, that is more trading more decrements.

・ Let denote the funds at the day. We assume that the initial value of the funds is, for simplicity.

・ denotes the funds the investor has paid after the decrement. We have

(4)

2.2. The Factors Affecting the Currency Exchange Market

An exchange rate at a given point in time represents the price of the involved currency with respect to a reference currency. It is clear that the currency exchange rates in the currency market depend on the both demand and supply for the currencies. There are two kinds of factors affecting the exchange rates which are: 1) Trade-related factor refers to the relative inflation rate, the income level and the government trade restriction; 2) Financial factor which refers to the relative interest rates and the capital flow restrictions (these two factors directly affect the demand and supply of the currencies). Thus the exchange rates should be varied with the two factors [9] . For each of the two factors, the relative inflation rate and the relative interest rate are the two main elements directly influencing the demand and the supply of currencies, other two main affecting factors should be the income level and the taxation, as clearly the taxation is the main instrument for the government to adjust the trade and the capital flow. Hence, in the present paper, we would like to focus on four main factors which are essential elements affecting the exchange rates.

The following diagram takes the US dollars and the British pounds as an example, showing the relationships of the four elements between the currency demand and the supply, respectively.

The vertical axis represents the price of US dollars in Sterling (i.e., changing of the exchange rate) and horizontal axis represents the quantity of US dollars demand by the Sterlings.

・ Solid line 1 represents the demand of the US dollars in the UK , when the price of the US dollars goes to expensive the demand of the US dollars will be lower, otherwise when the US dollars depreciates with the Sterlings the demand of the US dollars will be higher.

・ Solid line 2 represents the supply of the US dollars in the UK , when the price of the US dollars becomes too expensive the supply of the US dollars will get higher due to fewer US dollars would then buy more Sterlings, the UK commodities are cheaper therefore more supply of the US dollars to be purchased in the UK. On the contrary, when the US dollars depreciate with the Sterlings the supply of the US dollars should be lower. The crossing point of the two solid lines represents the equilibrium exchange rate.

・ Changes in the relative inflation rate will affect international trade activities, which influence the demand and the supply for currencies and therefore affect the exchange rates. The impact of rising the UK inflation rate while the US inflation remains the same are represented by the dotted lines 3 and 4, the increasing of the UK inflation rate would cause an increasing demand for US goods in the UK, leading to an increase in the demand for the US dollars in the UK. At the same time the inflation rises in the UK will reduce the export that indicates the supply of the US dollars will be reduced. Therefore, the crossing point of the lines 3 and 4 is the new exchange rate, which means the appreciation of the US dollars.

・ Changes in the relative interest rates also affect the investment in foreign securities, which influences the demand and the supply for currencies and therefore influences the exchange rates. The impact of rising the UK interest rates while the US interest rates remain the same are represented by the dotted lines 5 and 6. When the interest rates increase in the UK, the investors will reduce the hold of the US dollars and invest Sterling to earn the high interests in the UK, thus the demand of the US dollars is reduced and the supply is increased. If the price of the US dollars is reduced to be lower, then the investors would establish more bank deposits in the UK.The crossing point of the lines 5 and 6 is the new exchange rate, which means the depreciation of the US dollars.

・ The income level affects the demand amount of imports. Hence, it influences the exchange rate. Rising the income level in the UK while the US income level keeps the same will lead to increasing of the demand for US goods, but the supply of US dollars is not changed. Then the crossing point of the lines 7 and 2 is the new exchange rate, which shows an appreciation of the US dollars.

・ The taxation represents a kind of market frictions. It affects both the demand and the supply. The more tax the government has the less inflation occurs. Hence the taxation and the inflation rates have a negative correlation which means when taxation goes up the inflation rate goes down. As we known, the interest rates and the inflation rates have a negative correlation, we let taxation in the digram follow the change of interest rates as the dotted lines 5 and 6.

The above four elements are inter-dependent on one another. For example, when the income level goes up and the taxation goes up simultaneously, then that the inflation goes down leads to the interest rate goes up.

We let, and denote the inflation rate, the interest rate, the income level and the taxation, respectively, then the decrements we introduced in section 2.1 can be defined as follow

(5)

while when four elements goes down, we let; otherwise, we let.

2.3. On-Line Portfolio Strategy

The on-line portfolio is an active portfolio strategy, the investor using all the historical data of the day in the currency exchange market to predicate the portfolio in the day. We continue the notions and the notations from the subsection 2.1.

・ Let the portfolio for the day be denoted by

(6)

where f is a function of the returns of the currency and the previous portfolios.

・ Without the decrements, the whole investment can be increased by the following factor

(7)

・ Let be the proportion of the decrements to the initial funds on the trading day k, , such that

(8)

here we assume for.

・ With the decrements, the whole investment can be increased by the following factor

(9)

・ Let be the exponential growth rate of investment without the decrements

(10)

・ Let be the exponential growth rate of investment with the decre- ments

(11)

2.4. Decrements

For self-financing portfolios, for, the funds hold at the end of the day will be reinvested at the beginning of the day k. In our case, with the decrements, at the end of the day, the decrements are deducted from the investment (see the end of Subsection 2.1), the total funds in the currency is

(12)

At the beginning of the day, in terms of the new portfolio vector, the new transactions will be happen in the day. After new transactions, the funds of the investor will be reduced from to by the total amount of the decrements occurs in the day, that is, then the funds in currency i is

(13)

The decrement of the currency i is

(14)

We assume that the decrements remain the same for both sale and buy, then the total decrement at the beginning of the day is

(15)

In the day, we assume that the decrement depends linearly on the trading amounts of the day such that where is the identical percent factor. Then we have the following

(16)

We define, for and. We have the following inequality from (16)

(17)

On the other hand, we have that

(18)

If, we get

(19)

At the end of the day k, we set a portfolio contains m currencies in the currency exchange market as

(20)

where the entry of the vector is the ratio of the funds invest in currency i to the total funds, which is reached at the end of the day automatically, such that

(21)

Suppose that and. We define the “distance” between and as

(22)

As the funds at the end of the trading day k are equal to the beginning of the trading day, then we have that and combining the Equation (19) we get

(23)

From above, we known that at the beginning of the day the total amount of the decrement has related to, which means when the distance is equal to zero, no decrements occur, or one can say that the bigger distance implies the greater decrements, therefore less profits in a portfolio. On the other hand, shortening distance means reducing the decrements, hence more profit occurs in the portfolio.

3. Update Rules for On-Line Portfolio Selections

In the currency exchange market, investors usually prefer to exchange their currencies in portfolios to earn more profit, but simultaneously, investors need to pay more attention to those decrements linking to any costs incurred in the trading which might cause a gain reduction of the portfolios.

At the trading day, the profit, which is denoted by Z, of the portfolio is defined as the following function

(24)

where stands for the fund increments in the trading day with the portfolio vector and the prediction of the return vector at day, is the decrements incurred in the portfolio vector, and is a weight factor to balance the relation between maximising the funds and minimising the decrements.

The first form of that is given by the following

(25)

Next, suppose, then the second form of is determined via

(26)

which is just the first order approximation in the Taylor expansion of the function in the power of.

For, motivated by [2] - [4] , we specify it to be the relative entropy, defined as follows

(27)

which is clearly a positive continuous convex function of with the minimum extremum 0 at and the maximum extremum occurs when, for, if the smallest value is not unique then s represents the index of a smallest.

With these and from (25), (26) and (27), we have the following two update rules

1) Combining (24), (25) and (27) we get

(28)

2) Combining (24), (26) and (27) we get

(29)

It is clear that the function is concave in and other terms are either linear or constant in, so both and are concave functions of portfolio vector on the convex set H.

Applying the Lagrange’s method (see, e.g., [10] ) to (28) to maximise the function and to get the portfolio vector, one has then

(30)

where showed in (21), then the (30) is the update rule of the Factor of Fund Growth with Decrements (FFGD) for the trading day.

Another portfolio vector for maximising the function is given as follows

(31)

We call (31) the update rule of the Exponential Growth the of Fund with Decrements (EGRFD) for the trading day.

One can see in the update rules (30) and (31) that there are two selective elements and for the portfolio vector. The first is the parameter which has the following properties: the case that indicates the passive strategy; a smaller means the weak prediction of the currencies prices and the investors prefer to hold the present portfolio to avoid the decrements; while a bigger represents a stronger prediction of the currencies prices and the investors prefer to change the present portfolio to earn more profits. The second element is the prediction of the currencies prices. A high quality prediction is a power tool for investors to make a profitable decisions for the investments.

Remark 3.1. At the day the factor of fund growth as a measure of the fund increment, one can apply Euclidean distance between portfolio vectors and showing in (22) as a measure of the decrement.

Remark 3.2. In the real world currency exchange market, the investors prefer to remove the unprofitable currencies and to the add profitable currencies meanwhile to avoid the decrements, therefore, update rules (30) and (31) could be utilised.

4. Prediction of the Returns

In the currency exchange market, an important issue is to predicate the return of the investment. In this section, we would like to establish a method to select good currencies to replacing those bad ones in the portfolio. Our new prediction method is the so-called cross rate method, which concerns the order of the currencies returns rather than the returns of currencies themselves.

Here we only consider two currencies to discuss the order of the currency return for the aim of maximising the gain of the portfolio. To discuss the order of the currency, we introduce the cross rate step by step. The idea follows [2] .

Given a sequence of daily returns for two currencies, for, we define

(32)

as the order of the return vector, where indicates buy-and-hold the first stock, indicates buy-and-hold the second stock, and means no action for this portfolio. And also we define

(33)

We say that the sequence is strictly unequal if

(34)

for all. If there exits some, such that, then we say that there is a cross in the, where we define k as a cross position.

The segment is defined as

(35)

where J and K are integers such that. We define the cross number of for the two currencies to be the number of all crosses occur from the day J to the day K, which is

(36)

where stands for the cardinal number of the set.

Let the cross rate of be defined by

(37)

We divide the sequence into segments with identical length such as, , thus the corresponding cross rate sequence is defined as with the identical length L

(38)

4.1. The Cross Rate Method

Let, , we define

(39)

and define in the similar manner. For the stabilisation of the cross rate sequence in the sense that, , , and do not depend on n, we need

(40)

We outline three steps to get the prediction of a.

・ To estimate by. We have two cases for

(41)

For, for,

(42)

where and are two constants.

・ One can predict the order of the return of the currencies, here we predicate the order as following

(43)

and

(44)

where indicates the predicated value in terms of for.

・ Follow the step 2 we have in day, hence we need to assign a which has the right order, such that. For evaluating with, we have several selections, for example, for MPO1

(45)

and for MPO2

(46)

From above three steps we get the for. This is named as the cross rate method (CR method in short) and is denoted by CR(MPCR, MPO,).

4.2. Adjusted CR(MPCR, MPO,)

In the last subsection, we develop the CR method for the strictly unequal sequence. Due to the matter of fact that in the realistic market, could be a equal sequence, we need to adjust the CR method under strictly unequal case.

We define segment as, where are integers, and, and we record the number of cross occurs from the day J to the day K, the so called cross number of

(47)

where

(48)

Clearly, is the closest price vector before and the order of the is not zero. Therefore, the cross rate of is

(49)

where

. (50)

Same as before, we divide the sequence into segments with identical length such that,. Thus, the cor- responding cross rate sequence with the identical length L is

(51)

Similar to the subsection 4.1, the prediction of is given by following three steps.

・ The prediction of the by using the

(52)

and

(53)

・ In terms of to predict as follows

(54)

and

(55)

・ For MPO1', we have

(56)

and for MPO2', we have

(57)

5. Main Results

5.1. The Cross Rate Scheme

For the segment, we define the rate of success of CR(MPCR, MPO,) as

(58)

and if

(59)

then CR(MPCR,MPO,) is called effective for the segment.

The investors can rearrange their portfolio in the profitable direction by using the two update rules FFGD (30) or the EGRFD (31) with effective CR(MPCR, MPO,) for the segment.

The entire sequence is called a profitable strategy under the FFGD and the EGRFD with CR(MPCR, MPO,), if CR(MPCR, MPO,) is effective for, as

(60)

Lemma 5.1. Assume either

(61)

or

(62)

then CR(MPCRi, MPOj,) with are all effective for the segment.

Proof. We only show that CR(MPCR1, MPO2,) is effective for when the condition (62) holds, the proof under the condition (61) of this lemma is similar. In fact, we note that the condition (62) implies that both and have a

close interval from to 1. When that means in the set

at least half points are cross position. In terms of the MPO2 for

one has that for, thus, we have more

than half of the correct order of the segment, such that CR(MPCR1, MPO2,) is effective for

(63)

□

By the above lemma, one can see that if both and belongs to the

same intervals, , or but not exactly the same, then CR(MPCRi, MPOj,

), , is effective for.

Next, we recall from [2] that for a sequence, if there exist some constant such that and are independent for any n, and, then one call the sequence finitely dependent. The following result is taken from [2]

Lemma 5.2. If a sequence is finitely dependent of bounded random variables and, for some constant c and for any, then

(64)

Based on this lemma, the profitability of the FFGD and the EGRFD can be obtained. We state the following

Theorem 5.1. Let the sequence of cross rate be finitely dependent.

(1) if

(65)

then the FFGD or the EGRFD with CR(MPCRi, MPOj,), become a pro- fitable strategy as.

(2) if

(66)

then the FFGD or the EGRFD with CR(MPCRi, MPOj,), turn out to be profitable strategies when.

Proof. We only prove case (1) and the proof of case (2) is similar. We let

(67)

for. Notice that the cross sequence of is a finitely dependent sequence, we have from Condition (65)

(68)

due to that if either (61) or (62) holds, then CR(MPCR1, MPO2,) is effective for, and thus

(69)

Next, applying Lemma 5.2 to (60), we have

(70)

This completes the proof. □

This theorem combined with Subsection 4.1 gives the reasons for the selection of the MPCR1 and the MPCR2.

Remark 5.1. In practice, aiming to get the high profit, one suggest investor to choose two currencies with one of and which are

greater than. For example, if investors select two currencies by,

then the portfolio strategy actually has

(71)

5.2. Universality of the FFGD and the EGRFD

The feature of universality has been discussed in many papers. Here we follow [2] to discuss the universality of our on-line portfolio selections. In fact, the universality of the FFGD and the EGRFD can be used for any portfolio strategies. Also, the universality of the FFGD and the EGRFD for the active strategy (hold-and-sale) is similar to that for the passive strategy. So as a flavour, we just take the buy-and-hold strategy for a single currency for consideration.

Let us define the exponential growth rate of investment of the currency as

(72)

then the corresponding exponential growth rate of investment with decrements of the FFGD or the EGRFD algorithm can be defined as follows

(73)

where for all k and i, is the ratio which represent,s at the day k, the closing price to the opening price for currency. For simplicity, we suppose that for all k,. Let us just state the difference between and in the following result, the proof follow almost the same as in the proof of Proposition 5.6 and Lemma 5.8 in [2] , so we omit the proof here.

Theorem 5.2. For any, we have

(a) for the FFGD algorithm (30),

(74)

(b) for the EGRFD algorithm (31),

(75)

(c) If (30) is the selection strategy, we have

(76)

(d) If (31) is the selection strategy, we have

(77)

where in (c) and (d) above is independent of k and it uniformly converges to zero at the same rate of when.

The best currency in the buy-and-hold portfolio will be selected by the two update rules FFGD and EGRFD step by step. In practice, we divide any fixed integer, i.e., into partition, in the following subsets

(78)

where is he smallest integer greater than or equal to the fraction,

With the above division, is divided into subsets. When the length of equals.

Let us finally consider the sequence of the return and portfolio vectors in terms of the updates rule EGRFD (31) for exponential growth rate of investment with decrements. Suppose that each element of is bounded discounted by a small. We let be a function of i which decreases to zero as. Then apply (60) to each segment, and by Theorem 5.2 with being replaced by, we have

(79)

where is the last segment length and

(80)

With the similar approach, we have for the FFGD

(81)

Hence, we get following corollary

Corollary 1. A universal portfolio strategy w.r.t.the set of all buy-and-hold portfolios can be represented as the FFGD or the EGRFD algorithm with the linear prediction (containing the prediction under EMH). In a long-term investment, the exponential growth rate of funds with decrements in terms of the FFGD or the EGRFD algorithm is larger or equal to the exponential growth rage of funds achieved by the single best currency.

Remark 5.2. When, there is no action with the investors or the confidence of prediction is low hence the investor perform the buy-and-hold strategy. We showed that on the asymptotic properties of our portfolio update algorithms based on the exponential growth rate of funds with lower bound. And these algorithms show that when investor will gain more compare to.

6. Discussion

We have shown that the investors follow two update rules with the cross rate method to obtain more than half probability to reschedule the portfolio vector profitability and these update rules can also be considered as universality for the investors to measure on-line portfolios, by following the main ideas of [2] , but the difference is that our two update ruels with the decrements replace the transaction cost discussed in [2] .

This paper introduces a universal prediction method for on-line portfolio selection. We introduce the decrements first, which formed by four elements: the inflation rates, the interest rates, the income level and the taxation. These four elements strongly influence the volatility of the currency price during the transaction. In the present paper, we treat the decrements as any costs during the trading or we can say that any reduction of the profit during the transaction. To optimise the portfolio, we introduce two update rules with the decrements for any sequence of return vectors which maximise the increment of the investment and minimising the decrements.

We divide the sequence of the relative prices into the equal segments, and then we

predict the order of the currencies returns by the cross rate whether belongs to or for each segment. This method can determine amount of transaction, and it

is useful for the active portfolio strategy. More transactions in a trading day means that the currency has high price volatility, which implies greater decrement amount.

In our consideration, we focus on the on-line portfolio selection with the prediction method in the currency exchange markets. This strategy has showed success in [2] as a universal profitable selection strategy that pays more attention to the transaction costs. The prediction method in our thesis deals with the decrements as any costs caused by the price volatility depending on the inflation rates, the interest rates, the income level and the taxation. Hence, our decrement is specified as

We would like to mention that we have not yet tested our scheme developed in this paper with existing data from the currency exchange markets. Also, in the present paper, we focus only on the decrements. It would be interesting to extend our consideration in combining other factors, for instance, the transaction costs, the information costs, etc., just mention a few. We plan to do these topics in our future work.

Acknowledgements

We thank the referee for constructive comments.

Cite this paper

Ren, P.P. and Wu, J.L. (2016) On-Line Portfolio Selection for a Currency Exchange Market. Journal of Mathe- matical Finance, 6, 471-488. http://dx.doi.org/10.4236/jmf.2016.64038

References