Journal of Mathematical Finance
Vol.06 No.03(2016), Article ID:69374,10 pages
10.4236/jmf.2016.63030
On Steady Dividend Payment under Functional Mean Reversion Speed
Adeline Peter Mtunya1*, Philip Ngare2, Yaw Nkansah-Gyekye1
1School of Computational and Communication Science and Engineering, Nelson Mandela African Institution of Science and Technology, Arusha, Tanzania
2School of Mathematics, University of Nairobi, Nairobi, Kenya

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 April 2016; accepted 29 July 2016; published 2 August 2016
ABSTRACT
We study how firms’ management can ensure steady dividend growth and payout to the shareholders in an emerging market. We create the dividend equalization reserve account whereby during high profit some amount of money is kept in order to top up dividends during deficiency. We use a mean reversion stochastic differential equation with a functional mean reversion speed to find the optimal dividend policy with optimal dividend equalization reserve. One of our results indicates that, it is optimal to pay high dividends when we have high mean levels. Also, we realized that a higher level of volatility which implies more dividend can be paid. And high dividend can also be paid as the interest rate rises but this is more significant when the firm makes profits above average. Lastly, we compared the buffer approach to a situation where hedging was not applied and found that the buffering approach is more suitable because it gives shareholders steady dividend payments.
Keywords:
Investment, Dividend Policy, Steady Payment, Functional Mean Reversion Speed, Stochastic Optimal Control

1. Introduction
Since the seminal works by Jeanblanc-Picqué and Shiryaev [1] and, Radner and Shepp [2] , there have been a number of literatures on the optimization of dividend policies of a firm. These literatures include studies by [3] - [5] among others. Dividend policy has been among the most critical company decisions, not only from the viewpoint of the company, but also from that of the shareholders [6] [7] . The firm financial managers deciding on the dividend increase, focus on maintaining stable or increased earnings aimed at sustaining steady dividend payouts [7] - [9] . Bistrova and Lace [9] further argued that the topic of dividend is under-researched in the developing countries, whereas according to Dewri and Islam [10] there are prevailing investor demands for dividend particularly in such countries. In fact, these investors consider dividends as the principal component of stock returns [11] , complying to the theory of bird-in-the-hand in which investors prefer dividends from stocks to capital gains [12] [13] . Most of investors in such countries are at infant stage and needs to grow.
In our study, we show how the firm’s financial managers can ensure a steady dividend payout growth for the shareholders in addition to optimizing the dividend policy. Most models found in the literature have mainly been concerned with addressing the approaches to maximize the dividend payouts [1] [4] [5] [14] . This approach has been particularly used to determine the market value of a firm which is defined as the present value of the future dividends [15] [16] .
Dividend policy is one of interesting topics in financial literature today [17] . A large literature on optimal dividend payouts applies controlled diffusion models while considering other issues such as risk, solvency restrictions and investment [3] [5] [16] . The paper by Højgaard and Taksar [3] provides a typical example of the studies that attempted to find a policy which maximizes the expected discounted dividends paid until bankruptcy. In the paper they considered a risky company such as an insurance company with investments strategy, risk control and dividend distribution scheme. They presented a model for risk management by choosing different business activities, however, the dividend payments remain unsteady. [18] consider the dividend and investment policies of a cash constrained firm that operate in an environment where equity trading is not feasible but has access to loans. In this situation a firm can raise fund only by issuing collateral debt when it runs out of liquidity. In their study they maximize the shareholders value through dividend and optimal debt issuance. Since by rule, debt cannot directly be used to pay dividend, steadiness in dividend payment is not assured. Akyildirim et al. [14] considered exogenous influences to a firm and shown how dividend payment changes, following the macroe- conomic fluctuations. They contended that firms tend to distribute more dividends when interest rates are high. This means that in a situation of fluctuating economy there would always be unsteady payment of dividends. We build on such studies to address the steadiness of the dividend payments. Which is a requirement by share- holders and in order to attract new investors [8] [9] .
Three facts mainly contribute to the significance of undertaking this study. First is that investors in emerging markets continuously demand for dividend [10] thus there is a need to pay dividend consistently, that is, the amount and frequency of payment should not be perturbed. Second, to such investors dividend is the primary motivation for investing in stocks [11] so firms’ failure to maintain steady and high dividend payments is a discouragement to the investors. This is likely to cause a general failure to the growing markets. Third, in such emerging markets, business is more affected by macroeconomic shocks and therefore firms cannot have stable levels of profitability which would have automatically ensured the steady dividend payments. This is why having steady dividend policies is very important under this context.
We therefore model dividend as related to profit rather than cash holding of a firm as it is common in other literatures. Also compared to most of the literature such as [1] [3] [14] [18] , we define the bankruptcy in some different way, that is, the company is bankrupt when it can not make profit and the buffer for hedging dividend is empty.
The paper is organized as follows: Section 2 gives model formulation, definition of the buffer and its dynamics, and definition of the objective function. In Section 3, we state and prove properties of the value function. We show that the value function for our objective function is unique, concave and thus can be a solution of the dynamic programming equation. In Section 4, we carry-out numerical experiment. We simulate the dynamic of the profits, the dividend payouts and the corresponding buffer levels; we present numerical illustrations of the value function and give a comparison of this buffer approach and a situation where hedging is not applied. In Section 5, we summarize results of our study and make a conclusion.
2. The Model Set-Up
Uncertainty is given by a filtered probability space 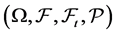 satisfying the usual assumptions and let
satisfying the usual assumptions and let 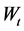 be one dimensional
be one dimensional 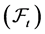 -Brownian motion. We consider a company whose profit level follows a Stochastic Deferential Equation (SDE) with an average of profitability
-Brownian motion. We consider a company whose profit level follows a Stochastic Deferential Equation (SDE) with an average of profitability 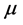 and volatility
and volatility 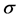 given by
given by
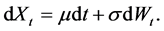 (1)
(1)
We denote by 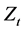 the cumulative amount of dividends paid from zero up to t, and by
the cumulative amount of dividends paid from zero up to t, and by 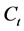 the total amount collected from the profit to the Dividend Equalization Reserve (DER) up to time t. Both processes Z and C are assumed to be nondecreasing,
the total amount collected from the profit to the Dividend Equalization Reserve (DER) up to time t. Both processes Z and C are assumed to be nondecreasing,  -adapted processes and have sample paths which are left-continuous with right limits. In addition to
-adapted processes and have sample paths which are left-continuous with right limits. In addition to 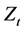 and
and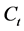 , we also incorporate a functional mean reversion speed,
, we also incorporate a functional mean reversion speed, 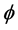 which virtually acts as the force that brings back the profit level to its mean by taking a reasonable amount of cash from the DER. The function
which virtually acts as the force that brings back the profit level to its mean by taking a reasonable amount of cash from the DER. The function 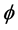 depends on the amount of dividend required and the profit made at a given time. So we eventually have the following model:
depends on the amount of dividend required and the profit made at a given time. So we eventually have the following model:
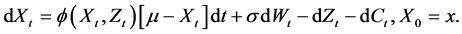 (2)
(2)
We denote the DER by B which is in actual sense the buffer whose increments or decrements depend on the difference between the profit X and the planned dividend Z at a specified time instance. The plan for dividend is such that always the dividend payouts will increase by the percentage 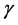 when profit is sufficient to pay the dividend otherwise the dividend maintains its previous level. When
when profit is sufficient to pay the dividend otherwise the dividend maintains its previous level. When 










The mean reversion speed 





We make the assumption that the company should make positive profits or have sufficient buffer for its survival, otherwise it has to undergo bankruptcy. We define the bankruptcy time 

Our objective is to maximize the performance index J given by

where the discount factor r is the constant interest rate.
Given an initial condition x, we denote the set of all admissible dividend and buffer increment scheme 





3. The Value Function
In this section, we present the analytical characterization of the optimal value function. Generally, we aim at maximizing the expected discounted dividend payments under steady scheme and the corresponding expected discounted buffer increments over all dividend and buffer increment strategies. We let 







used in the theorem.
Theorem 1. The value function v is the unique concave function satisfying the following:
1)
2) For every



Taking into account the time value of money, we assert that it is optimal to take a portion of profit to the buffer only when the profit is more than the required dividend. Also it is optimal to improve profit by a deduction from the buffer at most to the level of required dividend only when profit is less than required dividend. The firm should take no action as far as the profit made matches with the required dividend.
From the standard theory of singular control, we arrive to the following form of dynamic programming equation

of which we have the boundary condition 



We prove Theorem 1 by considering Equations (13) to (15) above. We begin by showing the existence and uniqueness, then we prove the concavity.
Proof. The general solution to the Ordinary Differential Equation (ODE) (14) is given by

where the real numbers





For future reference we note that
In order to verify the existence of the optimal value function as presented in Equation (14), we evaluate the Wronskian of 


Since the Wronskian is nonzero then we conclude that there exists a solution to Equation (14) of the form given in (16).
In order to prove the uniqueness of the value function, we state the following lemma
Lemma 1. The value function v as presented in (16) is unique if the constants

Now, every function v satisfying (13) and (14) is given by

To specify the parameters





which lead to



From the equations above we find that the value of z in Equation (24) is unique, then when considered with the other two Equations (25) and (26) show that the value function v is unique and thus we conclude that the HJB Equation (12) has a unique solution.
Next, to prove the concavity of the value function, we evaluate the second order derivative for the value function v and obtain

The inequality is due to the fact that




imply Equation (9) in the theorem.
From the theorem proved above we state the following corollary about the value function.
Corollary 1. Consider the maximization problem of the value function 




It is also worth pointing out that optimizing the dividend payments without this buffer approach as referred to [1] [14] leads to the following performance index

and the corresponding HJB equation is

with the boundary condition
4. Numerical Illustration
In this section, we discuss the sensitivity of the value function to the mean of reversion, volatility and interest rate for the given profit levels. We adopt the parameter values for the mean and volatility from Pierre et al. [18] and make an estimate for the interest rates. We start simulating the dynamics of the profits, the dividend payouts and the corresponding buffer levels at a given time interval. The simulation is presented in Figure 1 with initial conditions and parameter values specified. The figures thereafter are about experiments on the value function. At the end of this section we provide a numerical comparison of our results with a situation where hedging is not applied as given by (29) and (30) in the previous section.
In Figure 2, we find that the value function is higher when the difference between profit and dividend is made
Figure 1. Simulation of the dynamics of profits, dividend payouts and buffer with





Figure 2. Comparing value functions with



minimum, for the small and average profit values. However, when the profit is more than 70% of volatility above mean, a bigger gap between profit and dividend is optimal, thus more fund is taken to the buffer.
In Figure 3, we observe that, defining a higher mean of reversion for the profit will lower the value function and the difference widens as the profit becomes high. So it is optimal to have a mean level as minimum as possible. The case is different for the volatility as it is seen in Figure 4. Where the greater the volatility level, the higher the value function. The influence of volatility is similar to that of the difference between profit and dividend given above.
Figure 3. Comparing value functions with



Figure 4. Comparing value functions with



Moreover, for the case of the interest rate, in Figure 5, we observe that the higher the interest rate, the higher the value function as it is stated in [14] . However in this study we established further that, these differences between interest rates with respect to the value function, continuously grow as profit level increases.
Figure 6 illustrates a comparison of a buffering approach with the situation where steadiness of the payment is not implemented as presented in Equations (29) and (30). We find that for small values of profit, the buffering approach with a minimized difference between profit and dividend, gives a slightly lower value function than a
Figure 5. Comparing value functions with


Figure 6. Comparing value functions with




situation where optimization is done without a buffer. But for the higher profit values, buffering approach gives significantly greater value function as compared with a non-buffer approach. When the gap between profit and dividend is extremely large, then the value function is significantly greater for a non-buffer approach except for the very high values of profit.
5. Conclusions and Future Outlook
In our study, we have established strategies for a company that wants to optimize the policy of paying steady dividends to the shareholders. We consider the company that makes profit which can be modeled by a SDE with constant mean and volatility. The company creates a buffer account to hedge the dividend levels.
We find that the optimal dividend with hedging policy relies on four factors. The first is the gap between profit and dividend, whereby it is optimal to minimize the gap so as to pay more dividends. This means that the company can enhance the dividend by ensuring that there is a minimal difference between profit and the dividend to be paid. Secondly, we found that it is optimal to pay high dividends, when we can balance on mean levels that are high particularly for high profits. The third factor is the volatility in which we have found that a higher level of volatility implies more dividend can be paid. The last factor, is the interest rate, where we have illustrated that high dividend can be paid as the interest rate rises but we further establish that this is more significant when the firm can make profits above average.
We have also compared this buffer approach and a situation where hedging is not applied and found that the buffering approach is more suitable than the non-buffer approach because it satisfies more the shareholders by steady payments and when the profits are high more values are offered to the shareholders.
We suggest, a further research on use part of the amount that is left for other operations of the firm to expand the firm’s investment which may improve profitability. This investment can be in the risk free assets such as bonds. It is also possible to apply this steady scheme to investment, that is, optimizing the steady investment plan and leaving dividend distribution to depend on what remains after allocating profit to the investment plan.
Acknowledgements
We thank the editor and the referee for their comments. A. P. Mtunya study is supported by the Tanzania Commission of Science and Technology (COSTECH), The Nelson Mandela African Institution of Science and Technology (NM-AIST) and Mkwawa University College of Education (MUCE).
Cite this paper
Adeline Peter Mtunya,Philip Ngare,Yaw Nkansah-Gyekye, (2016) On Steady Dividend Payment under Functional Mean Reversion Speed. Journal of Mathematical Finance,06,368-377. doi: 10.4236/jmf.2016.63030
References
- 1. Jeanblanc-Picqué, M. and Shiryaev, A.N. (1995) Optimization of the Flow of Dividends. Russian Mathematical Surveys, 2, 257.
http://dx.doi.org/10.1070/RM1995v050n02ABEH002054 - 2. Radner, R. and Shepp, L. (1996) Risk vs. Profit Potential: A Model for Corporate Strategy. Journal of Economic Dynamics and Control, 8, 1373-1393.
http://dx.doi.org/10.1016/0165-1889(95)00904-3 - 3. Hojgaard, B. and Taksar, M. (1999) Controlling Risk Exposure and Dividends Payout Schemes: Insurance Company Example. Mathematical Finance, 2, 153-182.
http://dx.doi.org/10.1111/1467-9965.00066 - 4. Asmussen, S., Hojgaard, B. and Taksar, M. (2000) Optimal Risk Control and Dividend Distribution Policies. Example of excess-of loss reinsurance for an insurance corporation. Finance and Stochastics, 3, 299-324.
http://dx.doi.org/10.1007/s007800050075 - 5. Paulsen, J. (2003) Optimal Dividend Payouts for Diffusions with Solvency Constraints. Finance and Stochastics, 4, 457-473.
http://dx.doi.org/10.1007/s007800200098 - 6. Uwuigbe, U., Jafaru, J. and Ajayi, A. (2012) Dividend Policy and Firm Performance: A Study of Listed Firms in Nigeria. Accounting and Management Information Systems, 3, 442.
- 7. DeAngelo, H., DeAngelo, L. and Stulz, R.M. (2006) Dividend Policy and the Earned/Contributed Capital Mix: A Test of the Life-Cycle Theory. Journal of Financial Economics, 2, 227-254.
http://dx.doi.org/10.1016/j.jfineco.2005.07.005 - 8. Brav, A., Graham, J.R., Harvey, C.R. and Michaely, R. (2005) Payout Policy in the 21st Century. Journal of Financial Economics, 3, 483-527.
http://dx.doi.org/10.1016/j.jfineco.2004.07.004 - 9. Bistrova, J. and Lace, N. (2012) Dividend Stability and Sustainability in CEE Region. Proceedings of the 2nd World Sustainability Forum, 2, 1-8.
- 10. Dewri, L.V. and Islam, M.R. (2015) Behavioral Analysis of Investors’ Attitude towards Dividend Declaration in Developing Country—A Case of Bangladesh. International Journal of Business and Management, 11, 185.
http://dx.doi.org/10.5539/ijbm.v10n11p185 - 11. Al-Yahyaee, K.H., Pham, T.M. and Walter, T.S. (2011) Dividend Smoothing When Firms Distribute Most of Their Earnings as Dividends. Applied Financial Economics, 12, 1175-1183.
http://dx.doi.org/10.1080/09603107.2011.566177 - 12. Lintner, J. (1956) Distribution of Incomes of Corporations among Dividends, Retained Earnings, and Taxes. The American Economic Review, 2, 97-113.
- 13. Gordon, M.J. (1959) Dividends, Earnings, and Stock Prices. The Review of Economics and Statistics, 99-105.
http://dx.doi.org/10.2307/1927792 - 14. Akyildirim, E., Güney, I.E., Rochet, J. and Soner, H.M. (2014) Optimal Dividend Policy with Random Interest Rates. Journal of Mathematical Economics, 51, 93-101.
http://dx.doi.org/10.1016/j.jmateco.2014.01.005 - 15. Modigliani, F. and Miller, M.H. (1958) The Cost of Capital, Corporation Finance and the Theory of Investment. The American Economic Review, 3, 261-297.
- 16. Décamps, J. and Villeneuve, S. (2007) Optimal Dividend Policy and Growth Option. Finance and Stochastics, 1, 3-27.
- 17. Komrattanapanya, P. and Suntraruk, P. (2013) Factors Influencing Dividend Payout in Thailand: A Tobit Regression Analysis. International Journal of Accounting and Financial Reporting, 2, 255.
- 18. Pierre, E., Villeneuve, S. and Warin, X. (2014) Capital Investment and Liquidity Management with Collateralized Debt. TSE Working Paper, 2, 542.
NOTES
*Corresponding author.








