Received 25 September 2015; accepted 23 November 2015; published 26 November 2015

ABSTRACT

With increasing availability of data, in many situations it is now possible to reasonably estimate the probability density function (pdf) of a random variable. This is far more informative than using a few summary statistics like mean or variance. In this paper, we propose a method of forecasting the density function based on a time series of estimated density functions. The proposed method uses kernel estimation to pre-process the raw data followed by dimension reduction using functional principal components analysis (FPCA). Then we fit Vector ARMA models to the reduced data to make a prediction of the principal component scores, which can then be used to obtain the forecast for density function. We need to transform and scale the forecasts to ensure non-nega- tiveness and integration to one. We compared our method to [1] for histogram forecasts, on simulated data as well as real data from S&P 500 and the Bombay Stock Exchange. The results showed that our method performed better on both the datasets and the simulation using uniform and Hilbert distance. The time dependence and complexity of density function are different for the two markets, which is captured by our analysis.

Keywords:

Density Estimation, Functional Data Analysis, Principal Components Analysis, Vector ARMA

1. Introduction

Contemporaneous aggregation is often the only way to analyze temporal data, for example, considering the ob- servations of a variable measured through time in a population, e.g. the monthly output of firms in a country. If the individuals considered are not the same through time, then it is not possible to deal with the longitudinal data. However if one is interested in the overall evolution of all firms, histograms or densities can still be studied. [2] displayed a time series of the weekly returns of the firms in the S&P 500, summarized by histograms. This is an interesting precedent which shows that in some cases, histograms are preferable to averages or totals. [1] used smoothing and non-parametric method to estimate and predict histogram time series on S&P 500 data. In this paper, we follow-up on this idea, but replace histograms by density estimates. Kernel density estimates are smooth estimates of the probability density function and do not depend on the choice of end-points as opposed to histograms.

Density function estimation has been widely used in many areas such as finance [3] , energy market [4] and meteorology [5] . Although there is a rich literature on density estimation, there is very little work on density function forecast. The problem studied in this paper is different from the above references, in that, we consider replications of density estimates observed over time as opposed to just one density. To this end, we utilize the technique of Functional Data Analysis (FDA).

FDA is a popular statistical technique that treats entire curves as units of data (see [6] for an introduction). The theory of estimation of individual functions from discrete observations is quite well developed and these curves are eventually used in various applications like regression, clustering, time series etc.

The difference between a general function and a density function lies in the fact that density functions are nonnegative everywhere and their integral over the whole space is always equal to one. These restrictions pose challenges to using functional data methodology to densities directly. [7] [8] used a differential equation method to fit a smooth and monotone function and with the exponential transformation and post hoc procedure to finally obtain a fitted density function. [9] used FPCA to fit density functions and viewed them as independent and identically distributed to make statistical inference. Other possibilities are to deal with the cumulative density function or quantile function (see [10] ) instead of density, which also requires addressing challenges like smoothness, monotonicity and fixed support etc.

The paper is organized as follows. In Section 2 an overview of the methodology used in this paper is given, followed by a detail introduction of the three main statistical methods used: kernel estimation, Functional Principal Component Analysis(FPCA) and Vector Autoregression and Moving Average (VARMA). A simula- tion analysis is conducted on Section 3 to validate the performance of the proposed method and compare it to the performance of the method of [1] for prediction with a histogram time series using uniform and Hilbert norm distances. Two applications on main stock index of U.S. and India-S&P 500 and Bombay Stock Exchange are presented in Section 4 and 5 respectively. We present our conclusions in Section 6.

2. Methodology

Each dataset consists a set of 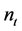observations from a distribution 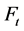and density 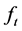for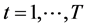. The aim is to obtain a forecast for the distribution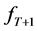. For each dataset, first we estimate a density function for each time point 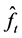using kernel based estimation method as described in detail in section 2.1. In the next step, we do FPCA on the density functions as explained in section 2.2. In section 2.3, we outline the modeling of the principal component scores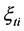’s as a multivariate time series and fitting a VARMA (p, q) model. The asymptotic results for time series of functional data are available in [11] . Since we are dealing with density functions, we need extra steps of transformation and normalization, so that the forecast functions are nonnegative and integrate to one. These are explained in section 2.4. The specification of distance between two functions is handled in section 2.5.

2.1. Kernel Density Estimation

Suppose 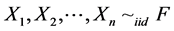and F is differentiable cumulative distribution function, that is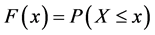. We are interested in estimating the probability density function (pdf)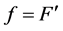. In the rest of the paper we use density to signify the pdf.

As a motivation of the following method, observe that:

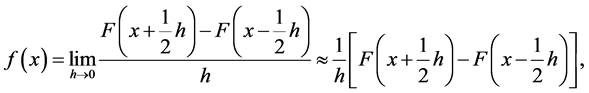
where the approximation holds for “small” h. Replacing F by the empirical distribution and h by a sequence 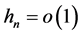as 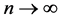we obtain the estimator:

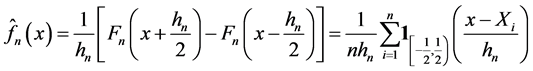. (1)

This density estimator can be understood as follows. First observe that the discrete empirical distribution

gives mass at. The point mass is replaced by a uniform distribution centered at, with support of

length. These uniform distributions are averaged to obtain the proposed estimator. Instead of spreading the

mass uniformly, an arbitrary pdf centered at can be used. This leads to a class of esti-

mators of the form:

(2)

where K is a pdf, i.e., for all x and. Such as estimator is called kernel estimator,

with the kernel K and bandwidth, both chosen by the user. Observe that automatically is a pdf, as we

have for all x, and the integration of over the real line is 1.

The choice of the kernel usually is not that crucial. The estimator in (1) is a special case with, the

uniform kernel. Some common choices for K are Uniform, Normal, Logistic and Epanechnikov.

The bandwidth is also called the smoothing parameter, as it determines how far the mass is spread out locally and hence how smooth the resulting estimator becomes. The choice of the bandwidth has a big influence on the performance of the estimator. For instance, for the uniform kernel, if the bandwidth is very large, the estimator would be flat. On the other hand, as the bandwidth becomes smaller, consists of larger spikes around the observations.As estimators of a pdf, both of the extreme cases are undesirable. The bias increases with increasing bandwidth, and the variance increases with decreasing bandwidth. This trade off indicates that an optimal choice of the bandwidth balancing between bias and variance, can be found through a minimization problem using standards like mean squared error. Under certain mild regularity condition, if as, then the kernel estimator as given in (2) satisfies:

(3)

where and. Therefore if then this asymptotic

MSE in (3) is minimized for with.

2.2. Principal Component Analysis of Functional Data

Consider a sample of T smooth random trajectories generated from a process f.

Following [12] , throughout we assume that f is an element of the Hilbert space endowed with the

inner product and the norm a.s. The sample trajectories are

modeled as realization of a stochastic process that has mean and covariance

function. There is an orthogonal expansion of G in terms of eigenfunctions

and non-increasing eigenvalues as:

where are the domain of each trajectory. The Karhunen Loève theorem then provides a representation of individual random pdfs, given by

(4)

where the are uncorrelated random variables with zero mean and variance, where.

The deviation of each sample trajectory from the mean is thus a sum of orthogonal curves with uncorrelated random amplitudes.

Often it is realistic to incorporate uncorrelated measurement errors with mean zero and constant variance

into the model, reflecting additional variation in the measurements, compare [13] . Let be the ob-

servations of the random function at time grids and additional measurement errors are assumed to be i.i.d and independent of the random coefficients i.e.,

(5)

where. In special cases, one might assume in addition that the are all jointly

normally distributed, but generally we do not make such assumption.

Under Equation (5) and with indicator function, we can get:

This implies that the smooth mean function and the smooth covariance function can be consistently estimated from pooling the sample of T trajectories and smoothing the resulting scatter plot. Well known procedure exists to infer eigenfunctions and eigenvalues [14] .

Processes f are then approximated by substituting estimates and using a chosen finite number of principal components. The specific number of principal components to be retained in the model is chosen by some optimization criterion like cross-validation, AIC, BIC or a scree plot.

2.3. VARMA Modeling

A sequence of random functions with values in is said to follow ARH (1) if it is stationary and such that

(6)

where is an white noise and the operator is linear and compact.

A higher order of autoregression process-ARH (p) (see [15] ), could now be defined as:

A natural extension would be to consider the series of functions follows the ARMAH (p, q) model with mean:

(7)

where

is white noise and are linear functions. The expansion in Equation (4) is still valid, as long as the process is second-order stationary. Combining (4) and (7) we have:

Using linearity of, this implies:

Combining all the terms involving and into and using vector representation, we have the following result:

(8)

where and. Since the columns of are orthonormal, we can left-multiply Equ-

ation (8) by to get:

which implies a VARMA (p, q) structure on the vector of principal component scores. We can use this theory to model the time series structure of functions as time series structure of the first few principal com- ponent scores, which largely reduces the complexity of the problem.

2.4. Rescaling and Non-Negativeness

As mentioned before, the difference between density function estimation and general function estimation lies in that density function are required to be non-negative everywhere and integrate to one.

However, the fitted function after FPCA estimation is not guaranteed to be positive everywhere. To address this, we took logarithm transformation of the fitted kernel density function before the FPCA estimation and used exponential transformation after the FPCA to guarantee the non-negativeness. In order to ensure that the fitted function integrates to one, we referred to [7] and imposed post hoc to rescale the fitted function.

2.5. Distance Measure between Two Functions

To compare the performance of FDA method and Arroyo’s method, we used two different distance measures between predicted functions and actual functions. These are the uniform distance and the Hilbert distance, defined as follows:

and

where f is the actual function and is the predicted function.

3. Comparison to Existing Methods

In [1] , the authors implemented exponential smoothing and k nearest neighbor methods to address the histogram time series (HTS) prediction problem. The authors defined the histogram data as:

where is the frequency for interval. The distance between two histogram is defined as

where or 2, is the order and is a distance measure such as Wasserstein or the Mallows

distance. It is assumed that the data points are uniformly distributed within each bin of the histogram. Under this

assumption, the CDF of a histogram, with is defined as:

where is the cumulative weight associated with the interval i.

By using this definition of the CDF of a histogram, the Wasserstein and Mallows distances formula can be written as functions of the centers and radii of the histogram bins:

.

3.1. Exponential Smoothing

The idea of exponential smoothing is to predict the next observation by a weighted average of previous ob- servation and its estimate. Let be a histogram time series, the exponential smoothing forecast is given by:

The authors show that the forecast is also the solution to the following optimization problem:

where is the Mallows distance. The use of the Wasserstein distance is not suitable in this case because of the properties of the median, which will ignore the weighting scheme. For t large, the exponential smoothing formula can be approximated by:

(9)

In the analysis below, we let and used the training data to estimate the. Subsequently we plug in

the estimated in the approximation rule in Equation (9) to get the prediction.

3.2. k-Nearest Neighbor

The k-Nearest Neighbor (k-NN) method is a classic pattern recognition procedure that can be used for time series forecasting. The k-NN forecasting method in classic time series consists of two steps: identification of the k sequences in the time series that are more similar to the current one, and computation of the forecast as the weighted average of the sequences determined in the previous step.

The adaptation of the k-NN method to forecast HTS can be described in the following steps:

1) The HTS, with, is organized as a series of d-dimensional histogram valued vectors, where

where is the number of lags and

2) The dissimilarity between the most recent histogram valued vector and the rest of the vectors is

computed by implementing the following distance measure

where is the Mallows or the Wasserstein distance of order q.

3) Once the dissimilarity measures are computed for each, we select the k-closest vectors to. These vectors are denoted by.

4) Given the k-closest vectors, their subsequent values, are averaged by means of the

barycenter approach to obtain the final forecast in the following minimization problem:

where is the weight assigned to the neighbor p, with and. For example, the weights

may be assumed to be equal for all the neighbors or inversely proportional to the distance between the last

sequence and the considered sequence.

In the analysis, we used equal weights when performing the minimization. The optimal parameter and, which minimize the mean distance error defined in the previous section in the estimation period, are obtained by conducting a two-dimensional grid search. Then the estimated parameter are plugged in the whole procedure again to get the prediction.

3.3. Simulation Results

Simulation was carried out to compare the performance of the proposed FDA method to the method of [1] for prediction with a histogram time series using uniform and Hilbert norm distances.

The data was simulated following Autoregressive Hilbertian (ARH) process as described in Equation (6).

Suppose satisfies. We can define the operator by the kernel

in the following way:

Specifically, in our simulation, we used and the following function with h as bandwidth:

(10)

Then our simulation consisted of the following steps:

・ Considered 16 different initial density functions: all beta distributed with integer values from 2 to 5 and integer values from 2 to 5. Also, considered 3 different bandwidths of h in Equation (10) as 0.05. 0.08 and 0.1. Therefore, there are totally 48 combinations.

・ Used Equation (6) with’s being i.i.d normally distributed with standard deviation equals to 0.05 to simulate 48 ARH (1) process each with length T equals to 250.

・ Used FDA method and Arroyo’s method to fit models on the first 200 density functions to predict the next 50 density functions.

・ Evaluated the performance of FDA method and compare the performance of FDA method and Arroyo’s method.

The performance evaluation of FDA method and comparison with Arroyo’s method are shown in Table 1. We observe that:

・ Most of the time (40 out of 48, 83%), FDA method chose the correct underlying process (ARH (1)).

・ The choice of number of principal components varied.

・ The FDA method outperformed Arroyo’s to a great extent in all metrics and both in uniform measure and Hilbert’s measure. Specifically, using uniform distance, FDA method is 90% less in average mean distance and 24% less in average standard deviation of distance than Arroyo’s method; using Hilbert’s distance, FDA method is 92% less in average mean distance and 89% less in average standard deviation of distance than Arroyo’s method.

4. S&P 500 Data Analysis

The Standard & Poor’s 500 (S&P 500) is a free-float capitalization-weighted (movements in the prices of stocks with higher market capitalizations have a greater effect on the index than companies with smaller market caps) index of the prices of 500 large-cap common stocks actively traded in the United States. It has been widely regarded as the best single gauge of the large cap U.S. equities market since the index was first published in 1957. The stocks included in the S&P 500 are those of large publicly held companies that trade on either of the two largest American stock market exchanges: the New York Stock Exchange and the NASDAQ. These 500 large-cap American companies included in S&P 500 capture about 75% coverage of the American equity market by capitalization. It covers various leading industries in United States, including energy (e.g. including com- panies like Exxon Mobil Corp.), materials (e.g. Dow Chemical), industrials (e.g. General Electric Co.), consumer discretionary (e.g. McDonald’s Corp.), consumer staples (e.g. Procter & Gamble), health care (e.g. Johnson & Johnson), financials (e.g. JPMorgan Chase & Co.), information technology (e.g. Apple Inc.), telecommunication services (e.g. AT&T Inc.), and utilities (e.g. PG&E Corp.). Though the list of the 500 companies is fairly stable, Standard & Poors does update the components of the S&P 500 periodically, typically in response to acquisitions, or to keep the index up to date as various companies grow or shrink in value. For example, TRIP (TripAdvisor Inc.) was added to replace TLAB (Tellabs Inc.) on Dec 20, 2011 due to the fact that Expedia Inc. spun off TripAdvisor Inc and WPX (WPX Energy Inc.) was added to replace CPWR (Compuware) on Dec 31, 2011 due to market cap changes.

The dataset we have is daily returns of all the constituents of the S&P 500 for 245 days from August 21, 2009 to August 20, 2010. This is the same data used by [1] and can be downloaded at http://pages.swcp.com/stocks/. Figure 1 shows the histogram of the first 4 days returns of all constituents. The first 3 days’ histograms look like a bell shape, indicating possibly normal distribution while the fourth day’s histogram is very centralized.

4.1. Kernel Density Estimation

After using the ksdensity function of Matlab on the S&P 500 data, we found out that over 40% of the fitted density function contains many extremely small (less than 0.0001) probability points, no matter how big bandwidth is, mainly due to some extreme returns each day. Example of fitted density functions that contain

many extremely small probability points can be seen on Figure 2. Retaining these points is a problem since we need to take logarithm of the extremely small numbers, which will make the fitting procedure later non- applicable.

Therefore, we drop the top 5% and bottom 5% fitted density points and keep the other 90% of it. After using this procedure, we get rid of the extremely small probability points problem completely. However, one thing we need to keep in mind is that the method in this section cannot be used for problems in extremes like value-at-risk and expected shortfall.

4.2. Principal Component Analysis of Functional Data

We use the PACE program in MATLAB ( [16] ) for this step. The program has AIC, BIC, and FVE (fraction of variance explained) method to determine to number of principal component functions. We observe that the AIC or BIC based method is not conservative enough and includes some extra functions which are very generic. Therefore, we decided to use FVE method and use scree plot to select the optimal number of principal com- ponent functions. See Figure 3 for the scree plot of the fitting of the S&P 500 data. Based on the scree plot, we chose 2 components for the fitting.

4.3. VARMA Modeling

We fitted multiple VARMA models of different order using Maximum Likelihood, Yule-Walker estimation methods as well as state-space models. These are not presented here, but are available from the authors on request. We observe that:

・ VARMA (1,1) is the best model when considering either AIC or BIC.

・ The AIC/BIC performance are usually better when using the Maximum Likelihood Estimation approach than the Yule-Walker approach, except when the model considered is VAR (1) model. In that case, the AIC/BIC performance are the same for both approaches.

・ The most promising procedure of state space model fitting in this data set is the brute force technique.

The daily S&P 500 Data has been reduced to a 2 dimensional time series in the previous procedure. Therefore, a VARMA (1,1) model only needs to estimate parameters, which has good power and accuracy. Based on this and the corresponding AIC/BIC performance, we decided to use VARMA (1,1) model for this data.

4.4. Comparison between FDA Method and Arroyo’s Method on S&P 500 Data

To compare the prediction result of FDA method and Arroyo’s method, we divided the S&P 500 sample into 185 days (around 75% of all data) as training period and 60 days (around 25% of all data) as prediction period. In the k-NN procedure, we also kept away the first 50 days’ data from the training period, since the estimation needs to begin with more data when k and d are large.

We used the training data to fit the FPCA model and obtained the corresponding 2 estimated principal component functions, the mean function, and the estimated principal component scores. Then we used VARMA (1,1) model of the principal component scores for next-day prediction. After getting the next-day prediction of principal component scores for 60 days, we combined those with the principal component functions and mean function obtained in previous training steps to get the predicted densities for each of the 60 days. Finally, we used Uniform Norm and Hilbert Norm to measure the distance between the predicted densities and the original densities. The distance between the predicted densities and the original densities (in both histogram and kernel form) using Arroyo’s method are also computed for comparison.

The time series plot of the Hilbert Norm distance of the 60 Days’ prediction period is shown in Figure 4. From the plot, we can clearly see that the one using FDA method outperforms the one using Arroyo’s method, using distance between the original density and the predicted density. It not only has a small value of distance on almost every day, but also has more stable performance.

The descriptive statistic of the Uniform Norm Distance and Hilbert Norm distance of the 60 days’ prediction period is given in Table 2 and Table 3. For Uniform Norm Distance measure, the distance using FDA method has smallest mean, second smallest median, and smallest standard deviation which indicates better and more stable performance. The fact that the minimum distance of the sixty days using FDA method is largest does not show any disadvantage of FDA method since we are looking at the overall performance across the 60 days. When it comes to Hilbert Norm Distance measure, the distance using FDA method has much smaller mean and median when compared with distance using Arroyo’s method. The standard deviation using FDA method is the largest, which is due to the fact that FDA method has result in a couple of much smaller distance values which actually indicates good performance.

In all, from the time series plot and descriptive statistic, the overall performance of FDA method is better than Arroyo’s method, in both Uniform Norm Distance measure and Hilbert Norm Distance measure.

5. BSE Data Analysis

The Bombay Stock Exchange (BSE) is a stock exchange located in Mumbai, India and is the oldest stock exchange in Asia. The equity market capitalization of the companies listed on the BSE was US$1.7 trillion as of January 2015, making it the 4th largest stock exchange in Asia and the 11th largest in the world. The BSE has the largest number of listed companies in the world with over 5500 listed companies. The dataset we had was weekly returns of 507 stocks of the BSE from from January 1997 to December 2004, totally 365 weeks. Figure 5 shows the histogram of the first 4 weeks’ returns of all the stocks. The first and third week’s histograms look like a bell shape, indicating possibly normal distribution while the second and forth week’s histogram is very centralized. There is also more skewness than in the S&P data.

5.1. Kernel Density Estimation

We used the same procedure as discussed in Section 1 on the BSE data. The weekly BSE data also suffers from the small probability points problem after applying the ksdensity function in Matlab (over 43% of the fitted density function contains many extremely small, less than 0.0001, probability points) and similar procedure was used to bypass this problem.

Examples of fitted density functions that contain many extremely small probability points can be seen in Figure 6.

5.2. Principal Component Analysis of Functional Data

FVE method of PACE package and scree plot is used again to select the optimal number of principal component functions. See Figure 7 for the scree plot of the fitting of the BSE data. Based on the scree plot and FVE procedure, we chose 4 components for the fitting.

5.3. VARMA Modeling

We did the similar VARMA modeling analysis on the BSE Data, namely fitted multiple models using different estimation methods and compared their AIC/BIC score. We observe that:

・ VAR (6) is the best model when considering AIC only.

・ VAR (1) is the best model when considering BIC only.

・ The AIC/BIC performance are usually better when using the Maximum Likelihood Estimation approach than the Yule-Walker approach, except when the model considered is VAR (1) model. In that case, the AIC/BIC performance are the same for both approaches.

・ The most promising procedure of state space model fitting in this data set is also the brute force technique.

・ Model chosen by AIC or BIC criteria has MA degree zero.

The daily BSE Data has been reduced to a 4 dimensional time series in the previous procedure. Therefore, a VAR (6) model needs to estimate parameters while a VAR (1) model only needs to estimate 16 parameters, which has far more power and accuracy. Based on this and the corresponding AIC/BIC performance, we decided to use VAR (1) model for this data.

5.4. Comparison between FDA Method and Arroyo’s Method on BSE Data

For BSE data, from time series plots (Figure 8) using uniform distance, we can clearly see that the one using FDA method outperforms the one using Arroyo’s method, using distance between the original density and the predicted density.

The descriptive statistic of the Uniform Norm Distance and Hilbert Norm distance of the 50 days’ prediction period is given in Table 4 to Table 5. Under Uniform Norm Distance measure, the distance using FDA method has better performance in all metrics. When it comes to Hilbert Norm Distance measure, FDA method has best performance in terms of mean and median although it suffers from the maximum being considerably large (4.2083) and has much larger standard deviation.

In all, from the time series plot and descriptive statistic, the overall performance of FDA method is better than Arroyo’s method, in both Uniform Norm Distance measure and Hilbert Norm Distance measure.

6. Conclusion

The paper proposes tools from Functional Data Analysis to forecast the probability density function. The technique is found to perform better than the method of [1] to forecast histograms in simulation and real data examples. For both real datasets, the density estimates have long tails. For the components of S&P 500, 2

principal components are enough to explain most of the variation in the shapes of the kernel densities. For the stocks traded on the Bombay Stock Exchange, 4 principal components are required. Also, the time dependence in the first dataset is ARMA (1,1), whereas for the second it is AR (1). This reflects the variation across markets (mature vs emerging), nature of stocks (large cap vs all) and frequency of observation (daily vs weekly). The method is flexible enough to accommodate these variations. In all the real data examples, forecasts using the FDA method are more efficient than the existing method.

Cite this paper

Rituparna Sen,Changie Ma, (2015) Forecasting Density Function: Application in Finance. Journal of Mathematical Finance,05,433-447. doi: 10.4236/jmf.2015.55037

References