Received 10 May 2015; accepted 3 July 2015; published 7 July 2015

ABSTRACT

Under the native-born model of default and the circular model of default, we take the price of credit derivatives into account. It’s supposed that the short-term market interest rates are based on Vasicek model in this article. Firstly, we calculate the price of default-free bonds in zero-coupon bond. Then, we give the default-intensity expressions under the two models. We calculate the prices of default-free bonds under the two default models. For different situations, we estimate the parameters by maximum likelihood estimation method and calculate the default probability of the company. From the analysis of the result, we find that the result conforms to reality. So the models of default intensity we suppose in the bond pricing are reasonable.

Keywords:

Default Intensity, Bond Pricing, Maximum Likelihood Estimation, Default Probability

1. Introduction

In the end of the 20th century, credit derivatives are developed as a way to transfer the credit risk of financial products, their value is developed from the bonds and other financial assets. The value of credit dervatives is to restructure credit risk. At the earliest, it appeared in the form of credit default swaps which were derived from corporate bonds. Credit default swap is a kind of insurance contract. Investors do not need to pay to the dealing party that is equal to the contract of credit default swaps in cash. In this way we can separate the credit risk from the cash flow. With the development of market economy, the forms of credit derivatives are enriched.

Because of the market requirement, the variety of credit derivatives becomes enormous rapidly. So its pricing becomes a very popular object of study. As usual, asset pricing is aimed at single case or default assets. When talking about the bonding pricing, we can consider it in the case of recovery rate, default time and market risk-free interest rate. The researching of recovery rate can refer to Brennan & Schwartz [1] and Jarrow & Turnbull [2] . When considering the researching of default time, we set the breach of contract as endogenous variable when establishing the model. If it is related to the asset value of company, we can use structuring model to establish models which are proposed by Merton [3] . The method is used in the pricing of credit derivatives. After that, Black & Schloes [4] generalized the model. If the assets value of company reaches the default border for the first time, we consider that the company has broken the contact or the agreement. The above of models are on conditions that the assets value of company submits to Brownian motion. When studying about interest rate, Merton proposed a single factor model. Then, Vasicek [5] put forward stochastic process with mean reversion to describe the dynamics of interest rates. The model has a closed formal solution.

Bai Yun-fen [6] uses a hyperbolic attenuation function to describe the contagion effects with breach of contract of credit risk. Jarrow & Yu [7] introduce the attenuation function with the types of hyperbola. Then, they use the function to represent the influencing process. With the passage of time, the delinquent party’s contagion influence to the other party decreased little by little. With the changing of measuring method, we get the two companies’ joint distribution and marginal distributions. So we can make a pricing of default-able bond and get the explicit solutions. They also generalized the hyperbolic attenuation function to general attenuation function. Then, we get the two companies’ joint distribution and marginal distributions. We price the default-able bond at this situation. But Jarrow & Yu didn’t consider the interest rate risk. This article is based on Jarrow & Yu’s native-default framework of default and Bai, Hu, & Ye’s [8] annular framework of default. The interest rate submits to the Vasicek model. We first suppose their respective default intensity and calculate the default-free bond price of zero-coupon bond. Secondly, according to the bond pricing formula, it requires Shreve’s [9] details to calculate the price. In the annular framework of default, we need to know each company’s joint density function and marginal density function. In order to get the two companies’ default-free bond prices, we use the functions with the bond pricing formula. While we calculate the probability of default, Duffie, Saita and Wang [10] proposed the maximum likelihood estimation method to obtain the companies’ probability of default. According to this method, under the default framework, we first estimate the parameters of stochastic intensity which we suppose. Then, we use the maximum likelihood estimation method to estimate the parameters and companies’ probability of default under the default framework. At last, we analyze the results with reality. It is concluded that the parameters which we suppose are reasonable.

2. Vasicek Model

In this article, the credit derivatives pricing is based on the Vasicek model. Because of this, we first introduce the Vasicek model in short. The Vasicek model is proposed by Vasicek (1977), to set a price of bond in the equilibrium model which is mono-factorial. We measure the market risk with Brownian motion. Because the model has explicit solutions, it is very convenient in the process of practical application. So this article we use the interest rate model to study the credit risk pricing model.

Definition 1 The rate in the Vasicek model satisfies the following stochastic differential equation:

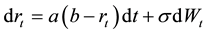(1)

where σ is the standard deviation, we use it to judge the random fluctuation. 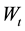is one-dimensional standard Brownian motion which measure the market risk. b is the long-term average of interest rate. For a long time, we find that the interest rates are always r hovered around b. Parameter a control the speed of interest rate r deviate from b and back to b.

Solve the differential equation above, we get that

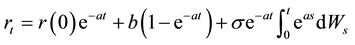(2)

Because ITO integral expectation is zero, so

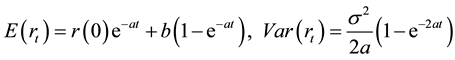(3)

To take the limit (3), we can get

(4)

where parameter b is the long-term average of interest rate. is mean square deviation. When the speed of

interest rate r deviate from b and back to b get faster, the mean square deviation of interest rate gets smaller.

3. Bond Pricing

This article is based on Vasicek model. We do some research on counterparty risk model under native-default framework of default and annular framework of default. We apply this interest rate model to bond pricing.

Definition 2 assume that probability space 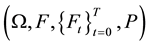meet the conditions, 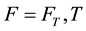is a prodi-

gious limitary number. p is the unique equivalent martingale measure in Hariso and Pliska. is state variable in probability space, it’s value range comes from.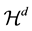

In order to be easy, we just consider two companies once time. The epidemic model could be complicated with many company situation and it’s not easy to export pricing formula. However, we couldn’t get the default parameter estimation. Assume that firm A and firm B each has zero coupon bond at the value of one dollar, expiration date is T, recovery rate is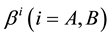. As usual, recovery rate is constant.

Assume that the firm A and firm B’s default process is 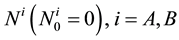and default time is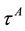, , 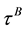default intensity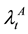, 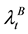should be non-negative random process. If the short-term market interest rate is, then, we get bond price of non-default zero coupon:

(5)

When comes to default-able bond, the pay should be

(6)

The first part in Equation (6) shows that when credit event happens, the debtor pay to the creditors. The second part in Equation (6) shows credit event doesn’t happen, the debtor pay to the creditors. So the price of default-able zero bond at time t equal to the discount price of the pay at time T. That is:

(7)

Equation (7) can translate into the following form:

(8)

Assume that short-term market interest rate is the unique macro state variable and the interest rate meet the Vasicek model

(9)

where, , k is constant, is standard Brownian motion.

is a Markov process, so there has function. We get

Because P is equivalent martingale measure, we use ITO formula. From that we get meet the following differential equation:

(10)

Boundary condition is whatever the r is, there should be F(T,r) = 1 and has solution like.

In the following part, we use shreve’s method to calculate the equation.

We can get

(11)

Take Equation (11) into above we can easily get, then, we also get. And we can get the following theorem.

Theorem 1 Assume the short-term market interest rate comply with (9). The value of zero bond is 1 dollar, due date is T, so we get default-free bond price, where and comes from Equation (11).

1) Native Cluster Framework

Assume that the default intensity of firm A and firm B meet the following relations:

(12)

(13)

where, is positive number, is real number.

Theorem 2 Assume that short-term market interest rate submits to Vasicek model, the default intensity of firm A and firm B obeys Equation (12) and Equation (13). If firm A and firm B don’t break a contract at time t, then, native firm A’s bond price at time t:

(14)

Firm B’s default-able bond price at time t:

(15)

where, are positive numbers, is real number.

Proof:

There is no relation between breach of contract and interest rate, so we can get that from Equation (8):

(16)

We take into Equation (16) can easily get firm A’s bond price at time t;

In a similar way, we know the default-able bond price of firm B at time t:

(17)

In Equation (17),

(18)

Take Equation (18) into Equation (17) we can just get the default-able bond price of firm B.

2) Annular Framework of Default

Assume that the default intensity of firm A and firm B meets the following relations:

(19)

(20)

where, is positive number, , is any real number that makes the default intensity positive.

Theorem 3 Assume that short-term market interest rate submits to Vasicek model, the default intensity of firm A and firm B obeys Equation (19) and Equation (20). If firm A and firm B don’t break a contract at time t, then, native firm A’s bond price at time t:

(21)

Default-able bond price of firm B at time t:

(22)

where and comes from Equation (11).

Proof:

By the bond pricing formula we get firm A’s bond price at time t:

(23)

When the default intensity of firm A and firm B obeys Equation (19) and Equation (20), , we get firm A and firm B’s joint density function:

(24)

Random, firm A and firm B’s marginal density function:

Now we need to calculate:

(25)

Take Equation (25) into Equation (23) we can get firm A’s bond price:

Because the firm A and firm B are a ring of default, so the calculation process is similar to the firm A’s.

4. Conclusion

This article explores the market short-term interest rates which conform to the Vasicek model. According to the existing literature, we want to get the default-free bond prices. Because it is a markov process, there is an explicit solution by using Shreve’s method. We suppose the form of default intensity with different framework of default. Under the native cluster model, we use the bond pricing formula to get the companies’ default-free bond prices. Under annular framework of default, in order to calculate the price of default-free bond, firstly, we get the two companies’ joint probability density and marginal probability density; then, we take it to the bong pricing formula; finally, we can easily get the default-free bond price under annular framework of default. In the last section, we estimate the probability of default by maximum likelihood estimation method. Through analysis and discussion, the parameters that we estimate correspond to reality. Of course, there are still many deficiencies in this article. For example, we should get further research through actual data. Calibration is carried out to the parameter estimation. If the parameter estimation is not so accurate through empirical analysis, it would produce deviation to the probability of default.

Acknowledgements

I would like to thank teacher Zhao. He helps me a lot in thinking and writing this article.

Cite this paper

HanghangZhou,DianliZhao, (2015) The Pricing of Credit Derivatives and Estimation of Default Probability. Journal of Mathematical Finance,05,243-248. doi: 10.4236/jmf.2015.53022

References