Received 11 May 2014; revised 15 June 2014; accepted 4 July 2014

ABSTRACT

In this paper, the model formulated incorporated stochastic variables such as bank loans and deposits as well as some deterministic variables: cash available, depreciation, capital expenditure, tax and costs, comprising variable costs and fixed costs. This paper assumes that the dynamics of bank loans and deposits at time t follow a geometric Brownian motion, therefore, it satisfies certain stochastic differential equations (SDEs) formulated on some probability space. On the other hand, the growth rate μ_L(t) in loan at time t, growth rate μ_D(t) in deposit at time t, and the variable cost η(t) at time t are assumed to be driven by mean-reverting Ornstein-Uhlenbeck processes. The SDEs of the dynamics of bank loans, growth rate in loans, bank deposits, growth rate in deposits and variable cost arising from the model were solved by means of the ItÔ Lemma. Discrete time approximations of the exact solutions of the SDEs were derived and used in a Monte Carlos simulation software.

Keywords:

Brownian Motion, Stochastic Differential Equation, Mean-Reverting Ornstein-Uhlenbeck Processes, ItÔ Lemma, Discounted Cash Flow

1. Introduction

In recent times, there has been a high level of bank consolidations especially in the emerging markets. Some of the benefits of these consolidations of the banking industry includes availability of funds for small and medium scale enterprises, opportunity for emerging banks to explore other regional and international markets, reduction in capital flight, massive and continuous innovation in the banking sector, externally-focused competition and restoration of confidence in the banking sector.

According to [1] , bank management focuses on four operational concerns. Firstly, the bank has to be liquid enough to finance its obligations to depositors. This aspect of bank management is called liquidity management and it involves the acquisition of sufficient liquid assets to meet the demand from deposit withdrawals and depositors payment. In addition, banks engage in liability management that entails the sourcing of funds at an acceptable cost. Thirdly, banks must have incentives to invest in assets that have a reasonably low level of risk associated with them. This process is known as assets management and aims to encourage investment in assets that have low default probability and strategies that are sufficiently diverse. Finally, capital adequacy management involves the decision about the amount of capital the bank should hold and how it should be accessed.

According to [2] , little has been written on the valuation of banks using the contingent claim approach. Most of the work done on bank valuation can be found in textbooks and practitioners’ guide which include ( [3] - [7] ). [8] asserts that bank valuation is one of the unresolved issues in financial research.

In corporate finance, it is not unusual to specify valuation models for particular types of firms. For example, [9] proposed a real option based valuation approach to natural resources companies, explicitly modeling the options to temporarily close, reopen and shut down the mine depending on the market price of the resource and [10] developed a model suitable to the traits of young, fast-growing firms, including little or negative current earnings but fast revenue growth.

The new models according to [2] , do not aim at introducing a new paradigm in asset pricing theory. Rather, the common features of these models is the attempt to better grasp the underlying characteristics of the business in which equity is the residual claim―when compared to standard approaches. For the same reasons, one can argue for a special valuation approach for banks.

The characteristics of the banking business motivating a distinct valuation approach can be as a result of the following: First, due to their central role for the economy, banking is typically a heavily regulated industry, covering a wide range of provisions, such as market entry, deposit insurance, reserve requirements, or capital structure. Second, banks operate on both sides of their balance sheets, actively seeking profits not only in lending but also in raising capital.

In their study, [2] proposed a valuation model for banks derived from [10] , Black-Scholes pricing model and the concept of matched maturity marginal value of funds (MMMVF). However, the model has a few shortcomings: it is abstracted from taxes, reserve requirements, minimum capital requirements and other regulatory factors, and it does not include non-cash items in valuation (depreciation, amortization, etc.).

In order for banks to successfully carry out these operational concerns, there is the need to continually value them. We adopt in this study the ( [11] [12] ) model with some modifications as in [13] . The valuation model adopted in this study takes care of the non-cash items (depreciation, accumulated property, plant and equipment and amortization) which are excluded in [2] .

2. Materials and Methods

A bank’s valuation begins with understanding its business model, which reflects its operating activities, sources of revenues and cost structure. According to [2] , a bank is an “institution whose current operations consist of granting loans and receiving deposits from the public”. As a result, it seeks to make profit on both sides of the balance sheet, a fact that is sometimes referred to as duality of the banking business. Our formulation involves stochastic differential equations, cash flow analysis and an indication of the simulation formula of the resulting model.

2.1. The Equations of the Model

In this section, the stochastic differential equations of the loan, deposit and cost dynamics are formulated and solved.

2.1.1. Dynamics of Bank Loan

Let 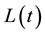be the loan given out by a bank at time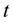. It is assumed that the dynamics of 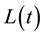is given by the stochastic differential equation:

(1)

The volatility of the return on the loan is assumed to converge to an average in the long-run, and is assumed to satisfy the ordinary differential equation:

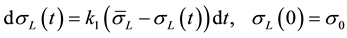(2)

For the growth rate 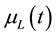of the return on loans in Equation (1), it is assumed that its dynamics is given by the following stochastic differential equation:

(3)

Finally, the volatility of growth rate of the return on loans is assumed to satisfy the ordinary differential equation:

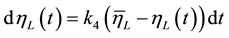(3a)

In the long run, the unanticipated volatility of growth rate of the return on loans is assumed to converge to zero, in which case, Equation (3a) reduces to:

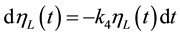(4)

According to [9] , the real world probability measure is converted to the risk-neutral probability measure. The dynamics of loans under the risk neutral probability measure is:

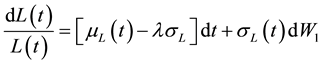(5)

where risk premium. It is Equation (5) that shall subsequently be solved to get its exact solution which will then be discretized.

2.1.2. Dynamics of Bank Deposit

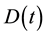Let be the bank deposit at time. We assume that satisfies the stochastic differential equation:

(6)

The volatility, is assumed to also converge to an average in the long-term, and it follows that:

(7)

The growth rate is assumed to satisfy the following stochastic differential equation:

(8)

Finally, the volatility of growth rate in deposit is assumed to satisfy the stochastic differential equation:

(8a)

In the long run, the unanticipated growth rate in deposit is assumed to converge to zero, in which case Equation (8a) reduces to:

(9)

Then, the dynamics of deposits under the risk-neutral probability is given by:

(10)

where risk premium.

We solved Equation (10) to get the exact solution for deposit and then discretized. is the covariance between the loans, deposits and market return. This relationship can be represented as:

(11)

where,

correlation between percentage changes in loans and returns of the market,

average return of the market,

standard deviation of the market,

risk free rate.

2.1.3. Dynamics of Variable Costs

The total cost of a bank will consist mainly of two components, the variable cost and fixed cost. The variable cost is the non-operating loan, which is a percentage of the total amount of loans. The fixed cost is the building and operating equipment cost. The fixed cost is assumed to be constant.

The total cost of a bank is therefore:

(12)

The variable cost function should be stochastic to reflect the uncertainty of future technology advancement and competition. Since only the variable cost would allow for the stochastic process, the variable cost can be written as:

(13)

The volatility of variable costs is assumed to satisfy the following ordinary differential equation:

(14)

Lemmas 1 and 2 are used to establish some of the formulae used in the simulation.

Lemma 1: The solution of the stochastic differential equation:

(15)

in the interval, where are constants and a standard Brownian motion is:

(16)

Remark 1: Note that, so, with. By applying this solution for every time step gives:

(17)

where.

Equation (17) is a recurrence relation; starting from, assumed to be known, it produces a random path for at the desired times.

Remark 2: Let and be the bank loans and deposit respectively at time. Then it follows from Lemma 1 that the solutions of the stochastic differential equation.

(18)

and

(19)

in the time interval, where are constants and, standard Brownian motions are

(20)

and

(21)

It follows from Equation (17), that Equations (20) and (21) can be written as:

(22)

(23)

Equations (22) and (23) are recurrence relations; starting from and, assumed to be known. They produce a random paths for and at the desired times. This will be used in the body of the simulation.

Lemma 2: Let be the solution of:

(24)

where, and are positive parameters and, a standard Brownian motion.

Then,

(25)

Remark 1: Equation (24) describes an Ornstein-Uhlebeck process.

Remark 2: Since, is a deterministic function, the stochastic process given by Equation (25) is a normal random variable with zero mean and variance:

By the Ito isometry, the variance of is:

(26).

Combining Equations (25) and (26), gives:

(27)

By applying this solution for every time step gives:

(28)

Remark 3: If the growth rates in bank loan and deposit and variable cost of the bank describes an Ornstein- Uhlenkeck process, then it follows from Lemma 2 that the solutions of the stochastic differential equations:

(29)

(30)

(31)

where are positive parameters, and and are standard Brownian motion are:

(32)

(33)

(34)

It follows from Equation (28) that Equations (32) (33) and (34) can be written as:

(35)

(36)

(37)

Equations (35), (36) and (37) are recurrence relations, starting from, and, which are assumed to be known.

Lemma 3: Let, and be the volatility of loans, deposits and variable cost of the banks. Then:

(38)

(39)

(40)

Lemma 4: Let and be the volatility of growth rate in bank loans and deposit. Then:

(41)

(42)

2.2. Cash Flow Formulation

2.2.1. Bank Revenue

The basic business of a bank is to generate funds through customer deposit and the giving out of these deposits as loans to its customers at a cost called interest. However, there are other sources of revenues for the banks. In this work, all the sources of revenue to the bank is depicted in Equation (43). The bank revenue can be defined as:

(43)

2.2.2. Loss Carry-Forward

In any new business start-ups, where there is no profit, the company is not expected to pay tax. However, the loss experienced in the current year is carried forward to the next year. Where there is no loss made, the after tax net-income of the company is given in Equation (44). The condition of whether profit is made or not is given in Equation (45).

With the bank revenue and cost known, the after-tax net income given as is:

(44)

2.2.3. Accumulated Property, Plant and Equipment

There are two variables that affect accumulated property, plant and equipment (P): the rate of capital expenditure and the corresponding rate of depreciation. Therefore, the accumulated property, plant and equipment can be expressed as:

(45)

2.2.4. Amount of Cash Available

In the banking sector, just like any other business venture, certain amount of money is set aside for the running of the company. The amount of cash available to the bank is actually used to reinforce the bank’s cash flow. When this amount is exhausted, the bank is said not to meet the financial requirements of his depositors. It is therefore imperative for banks to always have cash available. Where this is not available, the bank is said to be insolvent and this might lead to bankruptcy. This amount is as depicted in Equation (46).

The total amount of cash available for the company is given as:

(46)

2.2.5. The Value of a Bank

In this model, the value of a bank is a function of the state variables (loans, expected growth in loans, deposit, expected growth in deposits, variable cost, cash balance, loss-carry forward, accumulated property, plant and equipment), and time. This may be written as.

(47)

3. Result and Discussion

Due to path dependency of the model, the cash available at any point in time, which determines when bankruptcy is triggered, depends on the whole history of past cash flows. Similarly, the loss-carry-forward and the depreciation tax shields, which determine when and how much corporate tax the firm has to pay, are also path-dependent. These path-dependencies can easily be taken into account by using Monte Carlo simulation to determine the value of a bank. The value of a bank at an arbitrary time is given by:

(48)

Equation (47) follows from (48) by putting.

But,

Substituting these in (48), gives:

(49)

where

In the implementation of the model the study assumed that all the mean reversion coefficients are equal and their unique value is inferred from the expected half-life of their standard deviations. Equation (49) cannot be evaluated directly. This can be resolved using Monte Carlo simulation. To this end, the study partitioned the interval as follows:

.

Then, from (49):

(50)

where Number of partitions:

Equation (50) is used in the simulation.

4. Conclusion

In this paper, we successfully derived a model for the valuation of banks in terms of cash liquidity. As stated ealier, the equation of the model, Equation (49), could not be solved directly, as a result, we decided to use Monte Carlo simulation in finding an estimate for the value of a bank. With appropriate parameters estimated, Equation (50) can be used in estimating the value of a bank at an arbitrary time. Further work would require full estimation of the parameters needed to implement the model. We leave the development of a Monte Carlo simulation software and an application of the model to selected banks for future work.

Cite this paper

Enahoro AlfredOwoloko,Nicholas AmienwanOmoregbe,Michael AkindeleOkedoye, (2014) A Contingent Claim Approach to Bank Valuation. Journal of Mathematical Finance,04,234-244. doi: 10.4236/jmf.2014.44020

References

Appendix

A Nomenclature