Open Journal of Safety Science and Technology
Vol.04 No.03(2014), Article ID:49445,8 pages
10.4236/ojsst.2014.43015
Finite Size Scaling of Flame Spread along Randomly Distributed Combustible Cubes
Yukinobu Yoshida, Akihiko Ito, Hiroyuki Torikai
Graduate School of Science and Technology, Hirosaki University, Hirosakicity, Japan
Email: aito@cc.hirosaki-u.ac.jp
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 June 2014; revised 9 July 2014; accepted 9 August 2014
ABSTRACT
Flame spread in urban fire depends on quantity of combustible materials and their placement. The purpose of this study is to predict the flame-spread route by the rate of combustible area. In this experiment, we used combustible cube made from filter paper as a test sample, and combustible cubes and pores were randomly distributed in experimental area. Additionally, we examined non-uniform flame spread along combustible cubes in various porosities and experimental areas. Experimental results show that the flame-spread probability falls with increasing porosity, and despite uniform porosity, the flame-spread probability differs with the experimental area. When expanding the experimental area, less porosity is required to obtain zero flame-spread probability. To investigate based on finite size scaling of percolation theory for the change in porosity, we concluded that different thresholds exist for areas of all sizes. Because of the flame-spread progress stops in the thresholds, these porosities may be useful to predict fire hazard.
Keywords:
Percolation Theory, Finite Size Scaling, Flame-Spread Probability, Experimental Area, Porosity

1. Introduction
After a huge earthquake, multiple fires proliferate simultaneously in urban areas, while secondary damage is exacerbated by the spread of fire. In fact, several fires broke out after the Great Kanto Earthquake, Great Hanshin Earthquake, Great East Japan Earthquake and others. Urban regions include combustible areas such as wooden structures and plants, as well as the non-combustible, e.g. concrete buildings, roads, parks, and open areas, which mean that flames spread non-uniformly. Moreover, it is difficult to predict the flame-spread route because it may also be affected by the wind direction and terrain and the density of combustible materials. Figure 1 shows a photograph of an example—urban area in Japan and a binary image, where the urban area is divided into combustible and non-combustible areas. As shown in Figure 1, combustible and non-combustible areas of various sizes are randomly distributed in an urban area. When a fire starts somewhere, the phenomenon is divided into two cases. One involves the flame spreading and combustible materials burning out, and the other involves the flame self-extinguishing on the way. The threshold for burning out or self-extinguishing may be determined by the quantity and placement of combustible materials. Establishing safety by predicting the flame-spread route is important to reduce secondary damage caused by urban fires.
Many studies have been conducted focusing on flame spread along a uniform solid fuel load as a fundamental component of fire research [1] -[3] , but few have examined non-uniform flame spread in mixed combustible and non-combustible materials [4] . Some studies have focused on the application of percolation theory to non-uni- form flame spread [5] -[7] , while a few numerical simulations have also been conducted using a square lattice model [8] . However, discussing from an experimental perspective is rare. Accordingly, in our previous studies [9] -[11] , we conducted experiments concerning flame spread along a thin combustible solid with randomly distributed pores of different shapes and sizes. We also discussed the relationship between porosity and flame- spread probability based on percolation theory which treats connection of random media and refers to the “Introduction to Percolation Theory” written by Stauffer D. et al. about percolation theory [12] [13] . The latter is a probability theory dealing with properties of the connection of random media. A square lattice is shown in Figure 2(a), and the dots are written in some squares in Figure 2(b). This dot is called a site, and the group of neighboring squares occupied by these dots is circled as shown in Figure 2(c). Many of the sites become connected into a single large cluster, which spans the entire area vertically or horizontally due to an increase in site occupancy. This is called critical probability Pc and known as the percolation threshold. The value of Pc differs depending on the lattice shape and is about 59.3% in a square lattice of infinite size.
In this paper, we studied the flame-spread probability along combustible cubes with randomly distributed pores of various porosities. In addition, performing flame-spread experiments by changing the experimental area, we studied the effect of the size of the experimental area on flame spread by investigating the relationship between porosity and flame-spread probability. Furthermore, we introduce the porosity of flame-spread probability set to zero, and discuss the hazards of urban fire.
Figure 1. A photo of an urban area and a binary image of the urban area which is represented by combustible and non- combustible regions.

Figure 2. Definition of percolation and its site and cluster.
2. Experimental Methods
2.1. Experimental Apparatus and Procedure
A schematic of the experimental apparatus and combustible cube are shown in Figure 3. In this study, we used combustible cubes made from filter paper (ADVANTEC, No. 131, 250 µm thick) as a test sample. The experimental area was divided into a square grid, combustible cubes and pores were randomly arranged in each grid and the sample which arranged corner of the experimental area was ignited by a pilot flame. Experiments were conducted in atmosphere and a video camera (SONY, HDR-11, 30 fps) was set up above the experimental area to record the top view image of the flame spread. The experiment apparatus was also covered in vinyl sheeting to eliminate ambient disturbance of the flame spread. The test sample was a hollow cube of sides 20 mm, while the experimental area was square lattice of equivalent size, like the sample width. The number of samples to be placed to obtain arbitrary porosity was specified and their position was determined, using a random function to produce an experimental area of non-uniformly distributed pores and samples.
2.2. Experimental Condition
In this study, we selected ten different experimental areas, while the number of grids was 10 × 10, 20 × 20, 30 × 30, 40 × 40, 50 × 50, 60 × 60, 70 × 70, 80 × 80, 90 × 90, and 100 × 100. The flame-spread test was initiated by igniting a combustible cube placed in a corner of the experimental area. Figure 4 shows an example sample placement, where we defined the flame spread as the point when the flame had progressed from the top left (ignited sample) to the right or bottom sides. The flame-spread probability is defined as the value obtained by dividing the number of flame spreads by the number of flame-spread tests, as revealed by Equation (1):
 (1)
(1)
Number of flame-spread tests is the number of sample arrangement pattern which is 50 in this study. Porosity is defined as the percentage total pore area in the experimental area, as given by Equation (2):
 (2)
(2)
Figure 3. Schematic of the experimental apparatus.
Figure 4. Example of a sample placement and definition of the flame spread.
In this study, porosity was varied from 40% to 70% to investigate the relationship between flame-spread pro- bability and changes in porosity.
2.2.1. Jump of Flame
The previous study [9] -[11] confirmed the phenomenon whereby the flame spread of a thin combustible solid jumped over a non-combustible area. In this study using combustible cubes, flame spread also featured jumping over non-combustible areas. A flame-jumping test was conducted using two combustible cubes with a non- combustible area as a preliminary test shown in Figure 5 and ignited one sample. It was defined as jumping success if the flame of ignited sample was spread to the unburned sample, and the flame-jumping probability is defined as Equation (3):
 (3)
(3)
The relationship between flame-jumping probability and non-combustible distance was plotted in Figure 5. When the non-combustible distance is less than 5 mm, the flame can always propagate, but when the non-com- bustible distance exceeds 8 mm, the flame cannot propagate. Flame-jumping is related to the pre-heat length, Lh, ahead of the flame leading edge, which means a flame can traverse a non-combustible area in d < Lh, and not d > Lh as shown in Figure 6. We introduced the scale ratio S ≡ d/Lh (d: non-combustible distance, Lh: pre-heat length) to classify whether the behavior was flame jumping or not, namely whether the flame could jump the non- combustible area for S < 1, and not for S > 1. From these results, in this study with the square lattice of 20 mm width, no flame spread to traverse a pore.
2.2.2. Assumption of S < 1
The condition to satisfy S < 1, namely requiring d < Lh, was not met in this study. To study the effect of scale ratio on flame-spread probability, we assumed that the flame spread to the position shown in Figure 7, providing the condition of S < 1. Figure 7 is shown as the flame spread area of S > 1 and the flame-jumping area of S < 1. Where S < 1, in addition to the eight samples in contact with the combusting sample, we assumed the flame would spread to the four samples shown in orange color even if there were a pore between the samples.
Figure 5. Relationship between flame jumping probability and non- combustible distance.
Figure 6. Schematic of flame jumping over a non-combustible distance.
Figure 7. Flame spread and flame jumping areas.
3. Results and Discussion
3.1. Flame-Spread Trajectory
The cluster distribution for three different porosities and the flame-spread trajectory are shown in Figure 8. The image processing techniques of use for the flame-spread trajectory include normal speed photography (30 frames per second). In this figure, the black line is the flame-spread trajectory, which is depicted at intervals of ten seconds after ignition, while clusters mean area so finter connected pores, which prevent the flame-spread progressing. Pores form large clusters with increasing porosity until the flame is eventually extinguished when the cluster forms around the ignition point. For 40% porosity, the combustible area accounted for a large proportion, with little pore connection. For 50% porosity, the percentage combustible and non-combustible areas are half and half, with a large pore connection formed compared to the 40% porosity. Finally, in the case of 60% porosity, with a large pore proportion, the flame is swiftly extinguished. Figure 9 shows an example sample placement and the flame-spread trajectory at the time. Here, the L-shaped slit represents the cluster surrounding the flame source, where self-extinguishing occurred. In Figure 9, the red dashed line represents the L-shaped slit, while the samples shown in orange color are estimated to reach the flame spread. Accordingly, we conceived a method of calculating the extent of flame spread for the presence or absence of the L-shaped slit. In fact, there was no difference in the flame-spread areas to be calculated from the sample placement and observed from the flame- spread test respectively, therefore the following results were obtained from this method.
3.2. Flame-Spread Probability
Figure 10(a) plots the flame-spread probability as a function of different porosities in the number of grids, 20 × 20, 40 × 40, 60 × 60, 80 × 80 and 100 × 100 when S > 1. The flame-spread probability declines with increasing porosity in any number of grids. However, as the number of grids increases, the flame-spread probability becomes zero shows small porosity. To study the effect of experimental area in terms of its impact on flame-spread probability, we investigated porosity when the flame-spread probability become zero at any number of grids. Figure 10(b) shows the relationship of the number of grids and porosity when the flame-spread probability becomes zero. It can be seen that porosity when the flame-spread probability becomes zero declines with an increasing number of grids, and asymptotically approaches approximately 60%. It can be seen that in Figure 11(a), also S < 1, the flame-spread probability declines with increasing porosity as in the case of S > 1. However, the expanding flame-spread range means more porosity is needed to self-extinguish. In addition, the porosity when the flame-spread probability becomes zero declines with increasing number of grids, as in the case of S > 1 shown in Figure 11(b).
3.3. Scaling
We studied based on the percolation theory for the relationship shown in Figure 10(b) and Figure 11(b). According to the percolation theory, finite size scaling exists, which takes into account the finiteness of the area, and the following relationship is known between the threshold of the infinite region Pc and the effective threshold of the finite region P(L):
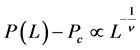 (4)
(4)

Figure 8. Flame-spread trajectory at 40%, 50%, and 60%, porosity of 10 × 10 grids.
Figure 9. Comparison of flame-spread test and flame-spread areas to be calculated from sample placement.


Figure 10. (a) Relations of flame-spread probability and porosities at S > 1; (b) porosity with zero flame-spread probability and number of grids at S > 1.


Figure 11. (a) Relations of flame-spread probability and porosities at S < 1; (b) porosity with zero flame-spread probability and number of grids at S < 1.
where Pc is the percolation threshold, L is the size of the area, and ν is a critical exponent (4/3 in two dimensions). Using a proportional constant C, Equation (4) can be rewritten as follows:

In this study, pores need to lead to the entire experimental area to stop flame spread, so we used the relation by correcting the coefficient (C) and regarded P(L) as porosity for which the flame-spread probability is zero. When approximating the experimental results by selecting a suitable value for C, P(L) can be expressed by Equation (6) for S > 1:

If the condition is S < 1, we found that the effective threshold at this time was represented by Equation (7):

Here, the threshold (Pc) has clearly changed compared to S > 1. The threshold of S < 1 exceeds that of S > 1 by about 10%, namely the risk of expanding flame spread increases. We considered that if the placement of the S > 1 and S < 1 samples were mixed, the threshold would be between both equations. These relationships are shown in Figure 12, where circular and square plots show zero porosity of flame-spread probability at S > 1 and S < 1, respectively. Solid and dotted lines represent the approximate curve of each of the plots.
4. Conclusions
In this study, we conducted flame-spread experiments using cubes of filter paper and mixed areas of pores. The following conclusions can be summarized here:
1) In the S > 1, L-shaped slit, the formed probability rises with increasing porosity, whereupon the flame- spread probability declines. However, where the number of grids differs, a difference also emerges in porosity when the flame-spread probability is zero. With extinguishing over 100 × 100 for 60% porosity and 20 × 20 for 70% porosity, just as described, it emerged that the porosity with zero flame-spread probability declined with increasing grids.
2) Similarly for S < 1, the flame-spread probability declined with increasing porosity, and the porosity when the flame-spread probability became zero decreased along with the increase of the number of grids. But, when compared with the same porosity, the flame-spread probability at the S < 1 is high value than the S > 1. And the porosity when the flame-spread probability becomes zero at the S < 1 is high percentage than the S > 1.
3) We determined the threshold of the porosity requirement for self-extinguishment within the finite region based on the percolation theory. The effective threshold can be expressed as follows:


We considered the fact that if S > 1 and S < 1 are mixed, the curve of the effective threshold is assumed to be between the above two equations.
4) We also considered the fact that the placement of combustible materials in the urban area is irregular, and the positions of S > 1 and S < 1 are mixed. Therefore, by providing a non-combustible area within the range of 60% to 70%, self-extinguishment result due to a non-combustible area, even if a fire occurs somewhere, will not generate significant fire-spread damage.
It is the future work of this study to make combustible areas more close to actual urban area by changing height of the combustible material and tilting the experimental area.
Figure 12. Relationship of porosity which flame-spread probability and number of grids, and the approximated curve.
Acknowledgements
We would like to thank S. Abe for his help with experiments and in preparing the manuscript.
References
- Fernandez-Pello, A.C. and Hirano, T. (1983) Controlling Mechanisms of Flame Spread. Combustion Science and Technology, 32, 1-31. http://dx.doi.org/10.1080/00102208308923650
- De Ris, J. (1969) Spread of a Laminar Diffusion Flame. Twelfth Symposium (International) on Combustion, 241-252.
- Kazuho, S., Kazumasa, M. and Toshisuke, H. (1984) Flame Spread over Paper in an Air Stream with a Velocity Change. Journal of Heat Transfer, 106, 707-712. http://dx.doi.org/10.1115/1.3246742
- Takashi, S. (1976) Summaries of Technical Papers of Annual Meeting. Architectural Institute of Japan, 1803-1804. (in Japanese)
- Toshiyuki, K., Takaaki, K. and Osamu, K. (2001) The Basic Study on the Evaluation of Disaster Mitigation Performance of the Local Area Road Network Based on Percolation Theory. Journal of Architecture and Planning, 549, 231-237. (in Japanese)
- Takaaki, K. (2002) Operations Research as a Management Science. Communications of the Operations Research Society of Japan, 47, 441-446. (in Japanese)
- Hiroshi, O., Hisashi, S., Masato, M. and Naoya, K. (2009) Flame-Spread Probability and Local Interactive Effects in Randomly Arranged Fuel-Droplet Arrays in Microgravity. Combustion and Flame, 156, 763-770. http://dx.doi.org/10.1016/j.combustflame.2008.12.013
- Akira, U. (2011) Application of Percolation Theory to Combustion Problems. Journal of the Combustion Society of Japan, 53, 145-152.
- Yukito, W., Akihiko, I. and Hiroyuki, T. (2009) Effect of Porosity on Flame Spread along a Thin Combustible Solid Randomly Distributed Pores. Sixth International Symposium on Scale Modeling, Proceedings (CD-Rom), Kauai, Hawaii, 13-16 September 2009.
- Yukito, W., Akihiko, I. and Hiroyuki, T. (2010) Flame Spread along a Thin Randomly Distributed Combustible and Noncombustible Areas. Proceedings of the Combustion Institute, 33, 2449-2455.
- Syuhei, A., Akihiko, I. and Hiroyuki, T. (2012) Flame Spread along a Thin Combustible Solid with Randomly Distributed Square Pores of Two Different Sizes. Modern Applied Science, 6, 11-19.
- Stauffer, D. (1985) Introduction to Percolation Theory. Taylor and Francis, London
- Stauffer, D. and Aharony, A. (1992) Introduction to Percolation Theory. 2nd Edition, Taylor and Francis, London.









