Open Journal of Marine Science
Vol.06 No.03(2016), Article ID:67924,18 pages
10.4236/ojms.2016.63030
Frequency and Surface Slope’s Effects on the Surface Displacement by Drilling Shallow and Deep Tunnels under Dynamic Loads
Arash Rostami1, Hamid Alielahi2, Mehdi Zare3, Kaveh Haghighi4
1Department of Civil Engineering, Islamic Azad University, Central Tehran Branch, Tehran, Iran
2Department of Civil Engineering, Islamic Azad University of Zanjan Branch, Zanjan, Iran
3International Institute of Earthquake Engineering and Seismology, Tehran, Iran
4Research Institute of Shakhes Pajouh, Isfahan, Iran

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 April 2016; accepted 27 June 2016; published 1 July 2016
ABSTRACT
Development and expansion of cities in one hand and increasing transport needs on the other hand have been causing underground constructions. So understanding the behavior of these structures is essential. Ground displacement around the tunneling area is one of the most important issues which have been studied by many researchers, while the effects of the slope behavior of the ground on the tunnel is paid less attention. This study will have analyzed the effects of frequency and surface slope on the surface subsidence caused by tunneling under dynamic loads (without structure). The results show that the frequency and surface slope have significant effects on the land displacements and the area surrounded by a tunnel.
Keywords:
Tunnel, Settlement, Slope, Depth, Dynamic Loads, Abaqus

1. Introduction
Due to the importance of the land displacement caused by shallow tunnels’ drillings in urban areas, many studies have been done on this subject by different researchers, since some decades ago. Pack (1969) did field studies on some excavated tunnels in different soils and showed that ground-level profiles’ subsidence statistical distribution is a normal curve (Gaussian) [1] . Then Atkinson and Potts [2] (1977), Clough and Schmidt [3] (1981), Mill and colleagues (1983) [4] and Leach (1985) [5] offered different relationships to estimate subsidence caused by tunneling operations. Pitilakis and colleagues in 2014 studied the seismic behavior of circular tunnels due to the interaction of ground structures; their main focus was on the tunnel responses, and their priority was tunnel’s behaviors. The results of this study show that in all analyzed cases, increased dynamic response of the tunnel in terms of deformation and lining in shallow tunnels is more significant [6] .
Alielahi and colleagues (2014) studied the use of boundary element method on time-domain for seismic response of buried cylindrical holes in soil. As a result of this research; the numerical results suggested that in a random SV wave with buried hole, horizontal component at the top of the cavity is reduced in comparison with displacement of the empty earth [7] .
Sika and partners examined the surface ground-domain under affections of buried and underground cavities and the ground-level domain was their main effort and activity. The results showed that the numerical methods suggest that the presence of buried craters on the earth has influence on the vacant land’s reinforce and this effect is not negligible [8] . Liu and colleagues in 2013 focused on the seismic behavior of buried tunnels with treating P and SV relay waves. The numerical results show that due to the effects of lined tunnels buried in the ground, linear shear modulus ratio of the average thickness is linear and has significant amounts [9] .
But most studies have been stated on the horizontal surface and few studies have done about the effects of the earth’s tilt on the subsidence which has been caused by tunneling operations. Heydari and his colleagues (2003) expressed that the land slope in the tunnel subsidence is negligible [10] . Ghazavi and Karimpour (2006) examined the slope of the surface subsidence caused by tunneling operations an announced that the land slope is not affected by this issue [11] .
Hasanloo Rad and colleagues in 2014 analyzed the surface slope effects on vertical displacement of tunnel’s crown and floor by ABAQUS 3D Tunnel software help, and mentioned that with increase in surface slope, displacement of tunnel’s crown and floor would have increase and the displacement of the tunnel’s walls at the bottom and top of the slope would encounter decrease [12] . Moosiv and Bayat in 2015 used software ABAQUS 3D Tunnel, and examined the surface slope on the surface subsidence and horizontal displacement of tunnel surrounding and they announced that any increase in ground-level slope will cause subsidence in surface level at the top of the tunnel and horizontal relocation with 6 m from the center of the tunnel at the bottom and top of the slope will be decreased or increased, respectively [13] . Rostami et al. [14] (2016) focus on investigating Effect of Tunnel Gate Shapes on ground settlements and acceleration they concluded that the rectangular tunnels had more effect in case of other tunnel shapes on ground responses. Rostami et al. [15] (2016) evaluated the effect of tunnel maintenances on surface and concluded that an umbrella method had significant effect on surface. Rostami et al. [16] (2016) evaluated effect of tunnels with different shapes on ground acceleration. Mousivan and Askari Ziarati [17] (2014) focused on depth of tunnel in different conditions with plaxis software. Also Alielahi et al. [18] (2015) worked on seismic ground amplification by unlined tunnels and concluded that The effect of the tunnel on the seismic ground surface response is gradually decreased or becomes insignificant with increasing the buried depth of the tunnel. Rostami et al. (2016) investigated Effect of Tunnel Gate Shapes with Similar Cross Section on Inserted Forces on Its Coverage and Soil Surface Settlement and conclude that the forces and settlements on rectangular tunnel shapes more than other tunnel shapes [19] . All the above issues are conducted in static loading state, and despite the expanded studies, evaluating the effects of dynamic loading is less considered. In this study, the effects of frequency and surface slopes on the displacements caused by tunneling under dynamic load will be discussed, using the software ABAQUS.
2. Geometric Features of the Model
Earth has a dust layer according to the specifications set in Table 1 [1] . Underground water level is lower than 50 meters from the ground.
In modeling with finite element method, choosing the model’s behavior is very important, because the stress-strain analysis is highly dependent on the behavioral model. To explain the soil behavior, the Hardening Soil Model has been used. The hardening model is a dough model which merges the shear hardening and volume hardening by using the united law to cap submission and using the in-united issue to non-diversion submission [13] (Figure 1).
Main features of this model can be summarized as follows:
・ Stress is dependent to stiffness according to the 3rd power (hard-tension power dependency)
・ The relationship between the strain and stress contribute to the deviant stress in the tri-axial tests
・ Segregation of initial loading in contrast with of reloading process
・ Failure according to Mohr-Coulomb criteria
・ Material parameters
There is a tunnel in the above land with a diameter of 8.85 m at a distance from the surface and the specifications are mentioned in Table 2 and Table 3. Also the thickness of the tunnel in the form of Lining has been defined in Table 4.
Table 1. Soil properties.
Table 2. Tunnel specifications.
Table 3. Tunnels specification.
Table 4. Lining specification.
Figure 1. Submission level of hardening soil model [13] .
3. Modeling
In this research, modeling has been done by using finite element software ABAQUS. Meshing is in average kind with 15-points, and in sensitive areas like the tunnel’s walls finer mesh has been considered (Figure 2 and Figure 3). Dynamic loads applied to the soil mass, are sinusoidal harmonic in range of 100 KN with different frequencies of 2, 4, 8 and 16 Hz and are applied to the bottom of the mass (Figure 4).
Figure 2. Soil meshing of shallow tunnel.
Figure 3. Soil meshing of deep tunnel.
Figure 4. Dynamic load applied to soil.
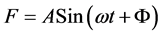 (1)
(1)
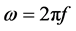 (2)
(2)
In the amplitude above, A is domain, w is angular velocity and f is frequency. The amount of the initial phase (Φ) is considered as zero. Standard boundaries and energy-absorbing barriers have been used in this model. Table 5 shows studies’ programs; in order to analyze the effects of frequency and slopes, 20 models have been considered.
4. Vertical Displacements of the Surface in Deep Tunnels
By analyzing the models, land surface subsidence curves changes are as forms 5 to 9 (Figures 5-9).
Table 5. Model’s specifications.
Figure 5. Surface subsidence-surface slope with 0 degree.
Figure 6. Surface subsidence-surface slope with 2 degrees.
Figure 7. Surface subsidence-surface slope with 5 degrees.
Figure 8. Surface subsidence-surface slope with 10 degrees.
Figure 9. Surface subsidence-surface slope with 15 degrees.
In static mode with increasing slope, vertical subsidence on top of the tunnel will have increase too, and this subsidence would decrease in the left side of the tunnel and would increase for the right side. In dynamic modes, with slope increase in equal frequencies, vertical subsidence in tunnel’s summit part will increase too, this subsidence would encounter decrease in left side of the tunnel and increase in right side; these changes are due to the decrease or increase of the overloads because of the transformations in surface slopes. In general we can say that the general view of vertical displacement changes in static mode and in dynamic mode is equal. According to the above charts f = 2 in all cases the maximum amount of subsidence is in summit and around the tunnel, this amount of frequency can be considered as dominant frequency and surface slope changes has no effect on the amount of dominant frequency.
4.1. Horizontal Displacements of the Left Side of the Deep Tunnel
The following charts are plotted for horizontal displacements, 6 m from left side of the tunnel center (Figures 10-14).
Figure 10. Surface horizontal displacement-surface slope is 0 degree.
Figure 11. Surface horizontal displacement-surface slope is 2 degrees.
Figure 12. Surface horizontal displacement-surface slope is 5 degrees.
Figure 13. Surface horizontal displacement-surface slope is 10 degrees.
Assessing the forms 10 to 14, it can be concluded that in static mode with increasing slopes up to 5˚, the horizontal displacement of the surface due to the lower overhead, decreases and in slopes greater than 5˚ the horizontal displacement enhances. In dynamic mode on the same frequency, the horizontal displacement of the surface would decrease with increasing slopes up to 5˚, and horizontal displacement would increase for angles greater than 5˚. According to the above graphs, in the f = 2 all cases of the maximum amount of horizontal displacement of the surface can be considered (except in the case that surface slope is 5˚). This frequency can be expressed as the dominant frequency.
4.2. Horizontal Displacements in Right Side of the Deep Tunnel
The following charts are plotted for horizontal displacement in 6 m from the right side of the tunnel center (Figures 15-19).
By examining the forms 15 and 19 we see that in a statically state by increasing the surface slope, the horizontal displacement of the surface increases, due to the increased overhead. In dynamic states with same frequencies, increasing the surface slope up to 5˚, causes decrease in the horizontal displacement and in angles
Figure 14. Surface horizontal displacement-surface slope is 15 degrees.
Figure 15. Horizontal displacement of surface-surface slope is 0 degree.
Figure 16. Horizontal displacement of surface-surface slope is 2 degrees.
Figure 17. Horizontal displacement of surface-surface slope is 5 degrees.
Figure 18. Horizontal displacement of surface-surface slope is 10 degrees.
Figure 19. Horizontal displacement of surface-surface slope is 15 degrees.
greater than 5˚, causes increases. According to the above graphs of f = 2, in all cases the maximum amount of horizontal displacement of the surface can be observed (except in the case in that slope is 5˚). This frequency can be expressed as the dominant frequency.
5. Vertical Displacements of Surface in Shallow Tunnels
By analyzing models, land surface subsidence curves’ changes can be seen as Figures 20-24.
In static mode with increasing slopes, upright subsidence will increase on top of the tunnel and decrease on the left and again increase in the right side of the tunnel. In dynamic state in same frequencies, with increase in the surface slope, subsidence will increase on top of the tunnel and also this subsidence will decrease on the left and increase on the right side of the tunnel; these changes are due to the increase or decrease of the overhead because of the slope changes. In general we can say that the general state of changes of vertical subsidence of surface in both static and dynamic states is equal. According to the above graphs f = 2, in all cases the maximum amount of subsidence is in the top and around the tunnel and this value of frequency can be expressed as the dominant frequency, and changes of surface slope have no effect on the dominant frequency.
Figure 20. Surface subsidence-surface slope is 0 degree.
Figure 21. Surface subsidence-surface slope is 2 degrees.
Figure 22. Surface subsidence-surface slope is 5 degrees.
Figure 23. Surface subsidence-surface slope is 10 degrees.
Figure 24. Surface subsidence-surface slope is 15 degrees.
5.1. Horizontal Displacement of Left Side in the Shallow Tunnel
The following charts are plotted for horizontal displacement with 6 m from the left side of the tunnel center (Figures 25-29).
Figure 25. Horizontal displacement-surface slope is 0 degree.
Figure 26. Horizontal displacement-surface slope is 2 degrees.
Figure 27. Horizontal displacement-surface slope is 5 degrees.
Figure 28. Horizontal displacement-surface slope is 10 degrees.
Figure 29. Horizontal displacement-surface slope is 15 degrees.
Studying forms 25 and 29 show that in the static state by increasing the surface slope, horizontal displacement of the ground on the left side of the tunnel will reduce due to the overhead. In dynamic states with same frequencies, horizontal displacement of the surface will decrease with increasing surface slopes up to 5˚, and will increases for angles greater than 5˚. According to the above graphs, f = 2 in all cases is the maximum amount of horizontal displacement of the surface (except in the case that the slope is 5˚). This frequency can be expressed as the dominant frequency.
5.2. Horizontal Displacements of the Right Side of the Shallow Tunnel
The following charts are plotted for horizontal displacement with 6 m distance of the right side from center of the tunnel (Figures 30-34).
By examining the forms 30 and 34 we can see that in a static state by increasing the surface slope, horizontal displacement of the surface would increase due to the rise in the overhead. In dynamic states with same frequencies,
Figure 30. Horizontal displacement-surface slope is 0 degree.
Figure 31. Horizontal displacement-surface slope is 2 degrees.
Figure 32. Horizontal displacement-surface slope is 5 degrees.
Figure 33. Horizontal displacement-surface slope is 10 degrees.
Figure 34. Horizontal displacement-surface slope is 15 degrees.
horizontal displacement of the surface will decrease by increasing the surface slope up to 5˚, and increases for angles greater than 5˚. According to the above graphs f = 2 in all cases is the maximum amount of the horizontal movement of the surface (except in the case with slope of 5˚). This frequency can be expressed as the dominant frequency.
6. Conclusions
In this study, the effects of frequency and slopes on the surface subsidence and horizontal displacement (a distance of 6 km of tunnel X) caused by tunneling under dynamic loads have been considered and summaries of the results are as follows
1) In the static mode vertical subsidence on top of the tunnel will increase with increase in surface slope, and this subsidence would decrease in the left side of the tunnel and increase in the right side.
2) Horizontal displacement of the surface beside tunnel is under affection of surface slope and this surface slope would cause decrease and increase of horizontal displacement for down side of the slope and up side of that, respectively.
3) In dynamic state with increase in the surface slope at same frequency, vertical subsidence on top of the tunnels would increase, and also this subsidence will decrease on the left side and increase on the right side of the tunnel. Horizontal displacement of the ground on the left and right side of the tunnel would decrease in the surface slope up to 5˚ and would increase in angles greater than 5˚.
4) Only one frequency in all cases (except when the slope surface is 5˚) causes the maximum displacement (f = 2) which is called dominant frequency. In the case where the surface slope is 5˚C, the dominant frequency is (f = 4), in other words it can be said that the dominant frequency change is effective on slopes. It is suggested to do complementary studies on the dominant frequency studies.
5) With increasing the depth, the amount of subsidence because of the tunnel excavations would reduce, it can be concluded that the depth is inversely related to the subsidence.
Cite this paper
Arash Rostami,Hamid Alielahi,Mehdi Zare,Kaveh Haghighi, (2016) Frequency and Surface Slope’s Effects on the Surface Displacement by Drilling Shallow and Deep Tunnels under Dynamic Loads. Open Journal of Marine Science,06,353-370. doi: 10.4236/ojms.2016.63030
References
- 1. Peck, R.B. (1969) Deep Excavation and Tunneling in Soft Ground. State-of-the-Art Report. Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico, 225-325.
- 2. Atkinson, J.H and Potts, D.M. (1977) Subsidence above Shallow Circular Tunnels in Soft Ground. Journal of Geotechnical Engineering Division, ASCE, 103, 307-325.
- 3. Clough, G.W. and Schmidt, B. (1981) Excavation and Tunneling. In: Brand, E.W. and Brenner, R.P., Eds., Soft Clay Engineering, Elsevier, New York, Chapter 8.
- 4. Mail, R.J., Gunn, M.J. and O’Reilly, M.P. (1983) Ground Movement around Shallow Tunnels in Soft Clay. 10th International Conference on Soil Mechanics and Foundation Engineering, Stockholm, 15-19 June 1983, 323-328.
- 5. Leach, G. (1985) Pipeline Response to Tunneling. Unpublished Paper.
- 6. Pitilakis, K. (2014) Seismic Behavior of Circular Tunnels Accounting for above Ground Structures Interaction Effects. Soil Dynamics and Earthquake Engineering, 67, 1-15.
http://dx.doi.org/10.1016/j.soildyn.2014.08.009 - 7. Hamid, A. (2012) Applying a Time-Domain Boundary Element Method for Study of Seismic Ground Response in the Vicinity of Embedded Cylindrical Cavity. International Journal of Civil Engineering, 11, 45-54.
- 8. Stefania, S. (2013) Ground Motion Amplification Due to Shallow Cavities in Nonlinear Soils. Natural Hazards, 71, 1913-1935.
http://dx.doi.org/10.1007/s11069-013-0989-z - 9. Liu, Q.J. (2013) Scattering of Plane P, SV or Rayleigh Waves by a Shallow Lined Tunnel in an Elastic Half Space. Soil Dynamics and Earthquake Engineering, 49, 52-63.
http://dx.doi.org/10.1016/j.soildyn.2013.02.007 - 10. Heydari, M., et al. (2004) Effect of Surface Slope, External Loading and Tunnel Cross Section Shape on Settlement of Digging Tunnel. 6th Congress of Tunnel, Science and Technology University, Tehran.
- 11. Ghazzavi, M. and Karimpour, H. (2009) Effects of Surface Slope on Settlement of Ground Profile and Lining Forces.7th Congress of Tunnel, Sharif University, Tehran.
- 12. Hasanloo Rad, M., et al. (2013) 3D Simulation of Effect of Surface Slopes on Durability of Tunnel. 2nd National Conferences of Crisis Management in Construction Industry, Engineering Research Center of Natural Disasters Shakhes Pajouh, Isfihan.
- 13. Mousavi, M. and Bayat, M. (2014) Investigation of Ground Slope on Surface Settlement Because of Tunnel Digging. 1st National Geotechnical Engineering, Ardebil, 22 October 2013, 101-115.
- 14. Rostami, A., Asghari, N., Askari-Ziarati, M., Jahani, S. and Shahi, B. (2016) Investigating Effect of Tunnel Gate Shapes with Similar Cross Section on Inserted Forces on Its Coverage and Soil Surface Settlement. Open Journal of Civil Engineering, 6, 358-369.
http://dx.doi.org/10.4236/ojce.2016.63030 - 15. Rostami, A., Kamali-Dehkordi, P., Askari-Ziarati, M, Jahani, S. and Lotfi, K. (2016) The Types of Tunnel Maintenancein Umbrella Arch Method. Open Journal of Civil Engineering, 6, 156-162.
http://dx.doi.org/10.4236/ojce.2016.62014 - 16. Rostami, A., Askari-Ziarati, M., Jahani, S. and Shahi, B. (2016) Evaluation of Seismic Behavior and Earth’s Surface Acceleration, by Interaction of Tunnelswith Different Shapes andDifferent Types of Soils. Open Journal of Civil Engineering, 6, 242-253.
http://dx.doi.org/10.4236/ojce.2016.62022 - 17. Mousavi, M. and Askai Ziarati, M. (2014) Effect of Slope on Shallow Tunnels under Dynamic Loads. 1st Engineering Congress and Evaluation of Development Projects, Gorgan, 5 May 2014, 159-210.
- 18. Alielahi, H., Kamalian, M. and Adampira, M. (2015) Seismic Ground Amplification by Unlined Tunnels Subjected to Vertically Propagating SV and P Waves Using BEM. Soil Dynamics and Earthquake Engineering, 71, 63-79.
http://dx.doi.org/10.1016/j.soildyn.2015.01.007 - 19. Rostami, A., Asghari, N., Askari Ziarati, M., Jahani, S. and Shahi, B. (2016) Investigating Effect of Tunnel Gate Shapes with Similar Cross Section on Inserted Forces on Its Coverage and Soil Surface Settlement. Open Journal of Civil Engineering, 6, 358-369.
http://dx.doi.org/10.4236/ojce.2016.63030




































