Open Journal of Marine Science
Vol.05 No.01(2015), Article ID:52454,12 pages
10.4236/ojms.2015.51002
Trends of Shoreline Position: An Approach to Future Prediction for Balasore Shoreline, Odisha, India
Nilay Kanti Barman1, Soumendu Chatterjee2, Ansar Khan1
1Department of Geography and Environment Management, Vidyasagar University, Midnapore, India
2Department of Geography, Presidency University, Kolkata, India
Email: nilay@csws.in, scgeovu@yahoo.co.in, khanansar@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 September 2014; revised 2 November 2014; accepted 21 November 2014
ABSTRACT
The present study aims to analyze the shift in shoreline due to coastal processes and formulate available for best estimate of future shoreline positions based on precedent shorelines. Informa- tion on rates and trends of shoreline change can be used to improve the understanding of the un- derlying causes and potential effects of coastal erosion which can support informed coastal management decisions. In this paper, researchers go over the changes in the recent positions of the shoreline of the Balasore coast for the 38 years from 1975 through 2013. The study area includes the Balasore coastal region from Rasalpur to Udaypur together with Chandipur, Choumukh, Chan- drabali as well as Bichitrapur. Transects wise shoreline data base were developed for approximately 67 kilometers of shoreline and erosional/accretional scenario has also been analysed by delineating the shoreline from Landsat imageries of 1975, 1980, 1990, 1995, 2000, 2005, 2010 and 2013. A simple Linear Regression Model and End Point Rate (EPR) have been adopted to take out the rate of change of shoreline and its future positions, based on empirical observations at 67 transects along the Balasore coast. It is found that the north eastern part of Balasore coast in the vicinity of Subarnarekha estuary and Chandrabali beach undergo high rates of shore line shift. The shoreline data were integrated for long- (about 17 years) and short-term (about 7 years) shift rates analysis to comprehend the shoreline change and prediction. For the prediction of future shoreline, the model has been validated with the present shoreline position (2013). The rate of shoreline movement calculated from the fixed base line to shoreline position of 1975, 1980, 1990, 1995, 2000, 2005 and 2010 and based on this, the estimated shoreline of 2013 was calculated. The estimated shoreline was compared with the actual shoreline delineated from satellite imagery of 2013. The model error or positional shift at each sample point is observed. The positional error varies from −4.82 m to 212.41 m. It has been found that model prediction error is higher in the left hand side of river Subarnarekha. The overall error for the entire predicted shoreline was found to be 41.88 m by Root Mean Square Error (RMSE). In addition, it was tested by means difference be- tween actual and predicted shoreline positions using “t” test and it has been found that predicted shore line is not significantly different from actual shoreline position at (t132 = 0.278) p < 0.01.
Keywords:
Linear Regression Model, End Point Rate, Root Mean Square Error, Shoreline Change, Shoreline Prediction

1. Introduction
Shoreline shifting is the uncontrollable result of coastal erosion/accretion, the consequence of near shore cur- rents. With reverence to the sediment supply, a certain portion of coastline may have excess, be in balance, or have a discrepancy in its sediment budget. Enormous drop or boost in the sediment supply, in a little span of time or a stretched period, creates a shortage/excess in the sediment budget which causes shoreline shifting.
Multi-year shoreline shifting mapping seems to be an important task for coastal monitoring and appraisal. Recently, satellite remote sensing data in combination with Geographic Information System (GIS) is being used in shoreline extraction and mapping [1] - [3] . Several studies have already been done on shoreline change and prediction, such as empirical analysis relating to hard stabilization structures to beach dynamics [4] [5] analysis of natural beach loss and gain [6] identification of relative changes among coastal units [7] and process response of a shoreline [8] . Shifting in shoreline and rate of shoreline shifting have also been calculated by various studies. The general method regarding this comprises with field observations such as tide and wave properties measure- ments, revealing and assessment of shoreline from toposheets, aerial photographs and multi date satellite image- ries. Several models have been proposed for prediction of shoreline from comparison with historical data such as End Point Rate (EPR) model [8] Average of Rates (AOR), Linear Regression (LR) and Jackknife (JK) [9] . The EPR model is based on the supposition that observed past rate of change is the best approximation available for predicting future while LR model is based on robust linear prediction method which detects short-range changes in the long-standing trend. This process recognizes the linear and high-order polynomial model which best fits the data according to that Minimum Description Length (MDL) condition that determines the nature and regu- larities in observed data. The length of the data by which the data itself can be described is used for measuring such regularities [10] . Prediction of future position of coastlines, from multi-temporal satellite images, using these models are reliant on several influencing factors like accurateness of shoreline recognition (accuracy of satellite data and method used), time duration of shoreline data attainment, number of data points taken into consideration during the measurement of shoreline position and temporal variability of shoreline etc. [11] [12] .
Spatial modeling in respect to the competent chronological illustration of the dynamic coastal setting is an in- credibly demanding and challenging research. An extensive range of appliance can be made potential with the exact inference of chronological shoreline shifting rates. The prediction model regarding future shoreline shift- ing and its positions are very much necessary to efficiently resolve the shifting in the shoreline and to permit us to maintain the structural and financial losses in the coastal region. So, it is essential to generate a digital data- base of chronological shoreline position, with the help of standardized remote sensing and GIS technology as well as to generate a data record that can be used to make possible the present and future analyses of shoreline shifting. The present study involves an endeavor to appraise an investigative model for predicting the future shoreline position in order to monitor the shoreline shift along the coast in Balasore district of Orissa, India.
2. Study Area
The study area includes an unconsolidated coastal sector of Subarnarekha delta, extends from Rasalpur to Udai- pur. The study area covers an area of about 142519.76 hectors Stretching between 21˚20'25''N 85˚50'45''E and 21˚39'55''N 87˚12'37''E in Figure 1. From the administrative point of view, these areas cover three blocks along with seven police station of coastal part of Balasore district. On the other hand this area is also geomorphologi- cally productive, reach in habitat diversity and environmentally hazards prone under the events of tropical cyc- lones, tidal waves, climate change and sea level rise. The study area is surrounded in the north by Mayurbanja district, in the south by Bay of Bengal in the east by West Bengal state and in the west by Bhadrak district of
Figure 1. Location map of the study area with three blocks i.e. Balasore, Baliapal and Bhograi.
state Odisha. As a result of increasing coastal hazards mainly tropical cyclone and other allied coastal hazards, oceanic processes like transgression and regression and also due to affecting on physical aspects of the envi- ronment by different types of human activities (deforestation, unscientific agricultural practices, excavators works) shore line becomes shifted here much more frequently. Being a deltaic low lying coastal stretch this area is monotonously flat alluvium surface of ground level varying between 2.5 m to 3.5 m above MSL. The study area is mainly covered by the Holocene alluviums along with the recent Subarnarekha river’s deposition, which has a natural gradient to the east and south east direction with a high water holding capacity of brackish water environment. The pH of the soil is varies from 6.5 - 8.0 (pre monsoon) and 6.2 - 8.2 (post monsoon). The mon- soonal phase is much more significant in this area. The temperature experienced in a range of minimum of 9˚C in winter to a maximum of 38˚C in summer. Relative humidity is prevailing here in between 90% - 96% at most of the months. At the time of the low atmospheric pressure during summer and monsoon period wind dominant- ly blows from the offshore areas. There is no such forest cover but, some brackish environment floral species like Sesuvium Portolacrustum, Ipomia Bioloba and some herbs like Lantena camera, Akanthesia, Calatropis gigantia are found in the study area with some planted trees like Casuarina, Eucalyptus and Acacia auriculifor- mis and also some indigenous floral species like Coconut, Banana, Bamboo and Mango.
3. Modeling Shoreline Shifting
3.1. Data Base
Three satellite data were taken into contemplation spanning over 38-year time period (1975-2013). Multi resolu- tion satellite data such as Landsat MSS and Landsat TM-5 are used in this study because of the unavailability of same resolution imagery over the chosen period. The details of the satellite imagery, acquisition details and reso- lutions are given in Table 1.
3.1.1. Data Processing
Eight satellite imageries of the years 1975, 1980, 1990, 1995, 2000, 2005, 2010 and 2013 have been taken into consideration. Landsat MSS and TM-5 data sets have been acquired from USGS. Landsat MSS image of 1975 has been resampled to 30m to match the spatial resolution of Landsat TM-5 images of 1980, 1990, 1995, 2000, 2005, 2010 and 2013. All the data sets are projected in UTM projection with zone no 45 and WGS 84 datum. A reference line has been considered as base line and image of 1975, 1980, 1990, 1995, 2000, 2005, 2010 and 2013 have been co-registered using first order polynomial model with base data with 0.5 pixel Root Mean Square Error (RMSE) accuracy.
3.1.2. Shoreline Delineation
Automatic shoreline delineation is a complex process due to the presence of water saturated zone at the land- water boundary [12] [13] . In order to delineate the actual shoreline position, two methods have been imple- mented-image classification and Normalized Vegetation Indexing (NDVI) (Figure 2). The bimodal natures of histograms of MSS and TM images have been found to be two different peaks for land and water. According to histogram observation, images have been classified using the ISODATA classification (unsupervised) technique
Figure 2. Shoreline delineation by unsupervised classification and normalized vegetation index (NDVI).
Table 1. Details of multi resolution satellite date of acquisition and resolution.
and two classes (land, water) have been taken to differentiate the land and water interface. In the vegetation in- dexing processes, Normalized Difference Vegetation Index (NDVI) has been used to separate the land water margin. The pixels signifying the shoreline have been converted into vector layer to get the real shoreline posi- tion. The shoreline (2013), which obtained by the applying of above methods has been matched up to with the 40 ground control points (GCPs).
3.1.3. EPR Model for Shoreline Prediction
The shorelines experience both attrition and accumulation over an extensive range of spatio-temporal scales. The prediction precision of shoreline situation depends on the capturing of the chronological processes and gives the most excellent information concerning the future shoreline positions. In shoreline analysis research, extra- polation of a constant rate of change is the most commonly used method to predict the shoreline [14] . Shoreline shifting rates are recurrently applied to sum up the historical shoreline shifting and their expectations prediction. A number of methods have been used for prediction of shoreline position as a function of time, rate of erosion and deposition or sea-level rise such as non-linear mathematical models e.g. higher order polynomial, exponen- tial model, cyclic series models [15] . Among them, the most easy and practical ones are the End Point Rate (EPR) (Figure 3) and the Linear Regression (LR) models. In the present study, the EPR model has been imple- mented to predict the future position of shoreline of Balasore coastal tract.
The model is based on the assumption that the observed periodical rate of change of shoreline position is the best estimate for prediction of the future shoreline [8] and no prior knowledge regarding the sediment transport or wave interference is required because the cumulative effect of all the underlying processes are assumed to be captured in the position history [15] .
The position of the potential shoreline for a given data is investigated using the rate of shoreline shifting (slope), time space between observed and predicted shoreline and model intercept which can be expressed as
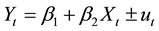 (1)
(1)
The subscript  is used to index the observations of a sample. The total number of observations, also called the sample size, will be denoted by
is used to index the observations of a sample. The total number of observations, also called the sample size, will be denoted by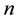 . Thus, for a sample of size
. Thus, for a sample of size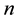 , the subscript
, the subscript 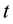 runs from 1 to
runs from 1 to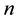 . Each observation comprises an observation on a dependent variable, written as
. Each observation comprises an observation on a dependent variable, written as 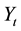 for observation
for observation , and an obser- vation on a single explanatory variable, or independent variable, written as
, and an obser- vation on a single explanatory variable, or independent variable, written as . The mathematical structure of the model which is necessary for model calibration is described in the following manner.
. The mathematical structure of the model which is necessary for model calibration is described in the following manner.
3.1.4. Position of Predicted Shoreline
The EPR model employs the shoreline taken out from the two end points of satellite imageries, the earliest 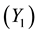 and the recent positions
and the recent positions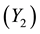 . If researchers use
. If researchers use  to indicate predicted shoreline positions,
to indicate predicted shoreline positions,  for time interval/date,
for time interval/date, 


Figure 3. Techniques of End Point Rate (EPR) calculation by arc distance and time between earliest and most recent shoreline position (After USGS, 2009).
(1) Rate of Shoreline Movement
The rate of shoreline movement for a given set of samples, 

(2) Intercept of End Point Rate
EPR intercept can be calculated as if only forward shoreline progradation has to be found

Shoreline position 

Since the end point line can extend beyond the most recent point


Hence, the shorelines extracted from 1975, 1980, 1990, 1995, 2000, 2005, 2010 and 2013 images which were segmented at 1 km interval and the location of the midpoint of each segments are sampled for the entire 67 km Balasore shoreline. The UTM coordinates (





The positional shift in the model (estimated shoreline of 2013) was validated with respect to actual image (extracted shoreline of 2013). The estimated shoreline was also validated with the 40 Ground Control Points (GCPs) collected from the field during the satellite overpass time and during high tide. The validation (location error in model estimated shoreline) was carried out in terms of RMSE [6] . The location errors at each sample point can be plotted as error vectors, which have the constituents in 


where 





4. Validation of EPR Model
The End Point Rate (EPR) model has been adopted for estimating the position of future shoreline. But prior to the prediction of future shoreline, the model has been validated with the current circumstances. To calculate the rate of shoreline shifting, the shoreline position in 2005 and 2010 was applied and based on this; the estimated shoreline of 2013 was calculated. The estimated shoreline was compared with the actual shoreline demarcated from satellite imagery of 2013 (Figure 4). The positional error varies from 4.82 m to 212.41 m. It has been found that model prediction error is very high at the mouth of Subarnarekha river. The overall error for the en- tire predicted shoreline was found to be 41.18 m (RMSE).
4.1. Long-Term Rates (2013-2030)
Long-term rates of shoreline change, in meters per year, were calculated at each transect by finding the slope of the best-fit line through all shoreline positions from the earliest (1975) to the most recent (1980, 1990, 1995, 2000, 2005, 2010 and 2013) (Figure 5). Long-term rates also were calculated without shorelines from the years of 1975 to 1980, 1990, 1995, 2000, 2005, 2010 and 2013 to examine the potential impact of including or ex- cluding these data on the measured rates of change. When calculating linear regression rates, at least three ob- tainable shoreline survey years were necessary at each transect. The linear regression method of calculating
Figure 4. Actual shore line position (2013) and predicted shoreline position (2030) along 67 km shoreline with 1 km linear space transect.
Figure 5. Transect wise distribution of coefficient of determination values as irregularity.
shoreline change rates assumes a linear trend of change between the earliest and most recent shoreline dates. In areas where a linear trend does not exist and shoreline positions have not progressed uniformly in one direction through time, it is expected that the resulting linear fit to the data will be poorer, and the linear regression rate will have a higher reported uncertainty. The metadata for the long-term transect shape files provide descriptions of the four attribute fields associated with the linear regression rate calculations. Additional information can be found in the Massachusetts Shoreline Change Mapping and Analysis Project, 2013 update [16] or Section 7 of the DSAS user guide [17] .
4.2. Short-Term Rates (2013-2020)
Short-term rates of change were calculated at each transect for the more recent 38 years of shoreline data (be- ginning in between 1975-1980 and ending with data from 1990-2013) using the linear regression method (Fig- ure 3). In addition, short-term end-point rates were calculated at any transect that had only two shorelines available within this time period. The end-point rate is calculated by taking the difference in shoreline position between the two dates and dividing that by the duration of time between surveys to report a rate in meters per year. The end-point rate simply represents the net change between the surveys (Figure 6), annualized to facili- tate comparisons with long-term linear regression rates. The short-term transect metadata files provide descrip- tions of the attribute field associated with the end-point rate calculation.
5. Shoreline Shifting over Time
5.1. Shoreline Dynamics during the Period of 1975-2013
The 67 km long Balasore shoreline has been delineated from the satellite imageries of different years (1975, 1980, 1990, 1995, 2000, 2005, 2010 and 2013) using the vegetation cover (NDVI) and image classification technique (Figure 2).
The delineate shoreline of 2010 was validated using 40 GCPs and the positional shift shows that classification method does better marking out of shoreline in contrast to NDVI. The positional shift is also articulated in terms of Root Mean Square Error (RMSE), which are 2.55 m and 4.62 m for the classification and NDVI techniques respectively.
It has been also noted that the shift in the classification-detected shoreline varied from 1.4 to 3.75 m while in NDVI the shift varied from 2.0 to 9.31 m. Based on this apprise, classification technique for delineating shore- line has been adopted for all other applications. It has also been found that the coast line of Balasore district is experiencing deposition. The position of shoreline at different years (Figure 7) shows the shifting of coast-line seaward. It also shows the erosional scenario of Balasore coast for the period from 1975 to 2010 indicating sig- nificant erosion in the northern part of the coast line (left bank portion of Subarnarekha river estuary) and also in thewestern and eastern parts of Burahbalang and Dugdugi estuary. It may be due to the hydrodynamics complexity of these areas. Whereas the mouth of the Subarnarekha river is gradually prograding towards the sea and rest part of the study area (southern part) is considerably stable in nature.
Figure 6. Transect wise End Point Rate (m/year) along 67 km shore line of Balasore coastal zone.
Figure 7. Shoreline position at different years from fixed base along same crenulations of shore line.
5.2. Future Shoreline Prediction Using EPR Model and Error Adjustment
Using the EPR model (Figure 3), the shoreline of the study area has been predicted for short term (2017) and long term (2030). In this prediction, shoreline shifting rate (Figure 8) has been calculated from chronological observations and disastrous impacts like tsunami and storm have not been taken into consideration. Figure 9 shows the past, present and future positions of shorelines.
The predicted shoreline indicates that the maximum erosion will take place in the northern part and no signifi- cant change has occurred in rest of the study area. The same observation was found in the change scenario of shoreline from 1972 to 2010, in Figure 10 which suggests that the cumulative effect of various processes like sediment transport system, littoral process, which is captured in the observed rate of change is relevant to predict the future shoreline.
An error adjustment procedure of EPR model has been proposed in this study. The positional shifts in 

The obtained results of the present study suggest that the utilization of remote sensing data in addition with the GIS technology and statistical technique are very appropriate for extraction of shoreline and its shifting calculation. Simple ISODATA binary classification technique is applicable for delineation of shoreline. The spatial modeling along with temporal representation of dynamic coastline of Balasore district signifies that the coastline of some places is suffering erosion and it has shifted inside.
The magnitude of erosion is higher in the northern part of the coastline in the left bank area of Subarnarekha river estuary and also in the estuarine part of river Dugdugi and Burahbalang, which is seen from the imagery of 1972 to 2010 and the model predicted shoreline also depicts the same. The southern part of the shoreline near Rasalpur, Joydevkasba is considerably stable, indicated by the same model. The validation of EPR model with
Figure 8. Transect wise rate of shore line change (m/year) along 67 km shore line of Balasore coastal zone.
Figure 9. Comparing the trend of shore lines in regards of earliest and forward predicted as 2020 and 2030.
image delineated shoreline was found to be useful. The cross validation shows that the model can predict con- sistent guesstimate of the shoreline position with satisfactory accuracy. The trend of the future shoreline shifting is matched with the present situation. A method for adjustment of model error is suggested in this work which can be validated to realize its efficiency.
6. Conclusion
Shorelines are constantly moving in reaction to winds, waves, tides, sediment supply, alterations in relative sea level and anthropogenic conducts. Shoreline changes are not invariable through time and recurrently switch from erosion to accretion and vice versa. Cyclic and non-cyclic processes alter the position of the shoreline over an assortment of timescales, from each day and seasonal reworking of winds and waves to transform in sea
Figure 10. Erosional scenario of Balasore shoreline from 1972 to 2010. The red colour depicts erosion, which is maximum in the north east part of the beach.
Figure 11. Areal and linear view of shoreline position regards to recent shore line position (2013). Long term and short time predicted shore line position with elapsed time 17 years and 7 years respectively.
level over a century to thousands of years. The shoreline “rate of change” statistic thus reproduces a collective summary of the processes that distorted the shoreline for the time period analyzed.
Shoreline shifting analysis of the Balasore coast was carried out using chronological shoreline arrangements spanning 38 years from 1975 to 2013. The Balasore coast was alienated into 5 regions for the purposes of this present study. Long-term and short-term linear regression rates of shoreline shifting were considered for a total of 67 transects covering 67 kilometers of shoreline. End-point rates were calculated in locations where there were inadequate data to use the linear regression method. The uppermost statistically considerable long-term and short term rates of shifting were experienced at Chandrabali coastal sector (Left bank side of river Subarnarekha).
The present work also facilitates us to comprehend the trends in shoreline behavior due to the influence of natural forces or anthropogenic alterations and how those trends are reproduced in shoreline shifting data. Shoreline shifting trends recognized in this study include (a) unidirectional long term shoreline movement (Chandrabali), considered by unremitting erosion or accretion, which can take place in both high-energy open ocean settings or low-energy settings; (b) fluctuating shoreline shifting (Choumukh), which are highly movable shorelines that have undergone both erosion and accretion on a long-term basis; (c) constrained shorelines in which shifting of the shoreline indicator is restricted by natural or anthropogenic features (Chandipur); and (d) anthropogenic shoreline rearrangement such as the infilling of embayments for development purposes (Subar- napur).
The shoreline shifting in the present coast experiences a greater range of variability only due to the frequently presence of tropical cyclone and allied coastal hazards. The significant fluctuations of short term and long term shoreline position (positional error 4.82 m - 212.41 m) in a particular transect is also the results of cumulative effects of different coastal hazards of this geomorphic part.
Acknowledgements
The authors are awfully indebted to Prof. John Pethick, World Bank Expert on coastal vulnerability, UK, for his precious comments and suggestions for improvement on the manuscript. We are also thankful to anonymous reviewers for their thoughtful suggestions to perk up this manuscript significantly. Finally, we thank our survey and research team for their generous cooperation in this study.
References
- Lee, J. and Jurkevich, I. (1990) Coastline Detection and Tracing in SAR Images. IEEE Transactions in Geosciences and Remote Sensing, 28, 662-668. http://dx.doi.org/10.1109/TGRS.1990.572976
- White, K. and El Asmar, H. (1999) Monitoring Changing Position of Coastlines Using Thematic Mapper Imagery, an Example from the Nile Delta. Geomorphology, 29, 93-105. http://dx.doi.org/10.1016/S0169-555X(99)00008-2
- Bertacchini, E. and Capra, A. (2010) Map Updating and Coastline Control with Very High Resolution Satellite Images: Application to Molise and Puglia Coasts (Italy). Italian Journal of Remote Sensing, 42, 103-115.
- Wright, H. and Pilkey, Jr., (1989) The Effect of Hard Stabilization upon Dry Beach Width. Proceedings of Coastal Zone ‘89, American Society of Civil Engineers. 676-790.
- Basco, D. (1991) Boundary Conditions and Long Term Shoreline Change Rates for the Southern Virginia Ocean Coastline. Shore and Beach, 59, 8-13.
- Paine, J. and Morton, R. (1989) Shoreline and Vegetation Line Movement, Texas Gulf Coast 1974 to 1982. The University of Texas at Austin, Bureau of Economic and Geology and Geological Circular, 89-1. 50.
- Siddiqui, M. and Maajid, S. (2004) Monitoring of Geomorphological Changes for Planning Reclamation Work in Coastal Area of Karachi, Pakistan. Advances in Space Research, 33, 1200-1205. http://dx.doi.org/10.1016/S0273-1177(03)00373-9
- Fenster, M., Dolan, R. and Elder, J. (1993) A New Method for Predicting Shoreline Positions from Historical Data. Journal of Coastal Research, 9, 147-171.
- Dolan, R., Fenster, M. and Holmes, S. (1991) Temporal Analysis of Shoreline Recession and Accretion. Journal of Coastal Research, 7, 723-744.
- Rissanen, J. (1978) Modeling by Shortest Data Description. Automatica, 14, 465-471. http://dx.doi.org/10.1016/0005-1098(78)90005-5
- Douglas, B. and Crowell, M. (2000) Long-Term Shoreline Position Prediction and Error Propagation. Journal of Coastal Research, 16, 145-152.
- Maiti, S. and Bhattacharya, A. (2009) Shoreline Change Analysis and Its Application to Prediction: A Remote Sensing and Statistics Based Approach. Marine Geology, 257, 11-23. http://dx.doi.org/10.1016/j.margeo.2008.10.006
- Ryu, J., Won, J. and Min, K. (2002) Waterline Extraction from Landsat TM Data in a Tidal Flat: A Case Study in Gos- mo Bay, Korea. Remote Sensing of Environment, 83, 442-456. http://dx.doi.org/10.1016/S0034-4257(02)00059-7
- Eliot, J. and Clarke, D. (1989) Temporal and Spatial Bias in the Estimation of Shoreline Rate-of-Change Statistics from Beach Survey Information. Coastal Management, 17, 129-156. http://dx.doi.org/10.1080/08920758909362081
- Li, R., Liu, J. and Felus, Y. (2001) Spatial Modelling and Analysis for Shoreline Change and Coastal Erosion Monitoring. Marine Geodesy, 24, 1-12. http://dx.doi.org/10.1080/01490410121502
- Thieler, E.R., O’Connell, J.F. and Schupp, C.A. (2001) The Massachusetts Shoreline Change Project―1800s to 1994. USGS Administrative Report to the Massachusetts Office of Coastal Zone Management, Boston, 26 p.
- Himmelstoss, E.A. (2009) DSAS 4.0―Installation Instructions and User Guide. In: Thieler, E.R., Himmelstoss, E.A., Zichichi, J.L. and Ergul, A., Eds., The Digital Shoreline Analysis System (DSAS) Version 4.0―An ArcGIS Extension for Calculating Shoreline Change: US Geological Survey Open-File Report 2008-1278, ver. 4.2. 81 p. http://pubs.usgs.gov/of/2008/1278/
















