Open Journal of Marine Science
Vol.04 No.04(2014), Article ID:50501,10 pages
10.4236/ojms.2014.44023
Extended (G'/G) Method Applied to the Modified Non-Linear Schrodinger Equation in the Case of Ocean Rogue Waves
Atock A. Nwatchok Stéphane1*, Daika Augustin2, Mbane Biouélé César2
1Department of Mathematics and Physics, National Advanced School of Engeneering, University of Yaounde I, Yaounde, Cameroon
2Department of Physics, Faculty of Science, University of Yaoundé I, Yaoundé, Cameroon
Email: *steph_atock@yahoo.fr
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 August 2014; revised 13 September 2014; accepted 24 September 2014
ABSTRACT
The existence of rogue (or freak) waves is now universally recognized and material proofs on the extent of damage caused by these ocean’s phenomena are available. Marine observations as well as laboratory experiments show exactly that rogue waves occur in deep and shallow water. To study the behavior of freak waves in terms of their space and time evolution, that is, their motion and also in terms of mechanical transformations that these systems may suffer in their dealings with other systems, we derive a modified nonlinear Schrödinger equation modeling the propagation of rogue waves in deep water in order to seek analytic solutions of this nonlinear partial differential equation by using generalized extended G'/G-expansion method with the aid of mathematica. Particular attentions have been paid to the behavior of rogue wave’s amplitude which highlights rogue wave’s destructive power.
Keywords:
Deep Water, Generalized Extended G'/G-Expansion Method, Rogue Waves

1. Introduction
During many centuries, rogue waves, unexpectedly high wave, strongly localized in space-time, have been widely reported all over the world. For a long time, they were thought to be a part of marine folklore, but with the development of instrumental measurements their existence has become evident and has been scientifically proven [1] - [4] . An important milestone in the understanding of rogue wave dynamics occurred in 2001, when two European Space Agency satellites detected more than 10 individual giant waves over 25 m high during only three weeks of monitoring of the world’s ocean [5] [6] . This evidence demonstrated that rogue events are not unique and highly improbable but occur regularly in the random wave field. Such extreme events are believed to have caused a number of marine accidents with subsequent pollution of large coastal areas, ship damage and human casualties [7] [8] .
The understanding of extreme and rogue waves have significantly advanced recently. A number of extreme and rogue wave studies have been conducted theoretically, numerically, experimentally based on field data [9] - [22] . It has been demonstrated that the contribution of high order nonlinear mechanisms such as the modulational instability of uniform wave packets [23] [24] may give rise to substantially higher waves than that predicted by common second order wave models [25] [26] .
Some authors [27] [28] are attempting to discover the probability of their appearances as well as studying the mechanism of their formation. Others have found exact solutions of nonlinear evolution equation (NLEEs) and have explained rogue waves phenomenon [29] -[32] .
Recently, Wang et al. [33] introduced an expansion technique called the (G'/G)-expansion method and demonstrated that it was a powerful technique for seeking analytic solutions of nonlinear partial differential equations. Bekir [34] and Zedan [35] applied this method to obtain travelling wave solutions of various equations. A generalization of the method was given by Zhang et al. [36] . Also, Zhang et al. [37] made a further extension of the method for the evolution equations with variable coefficients.
The main aim of this paper is to seek exact solutions of modified nonlinear Schrodinger equation modeling the propagation of rogue waves in deep water with extended G'/G-expansion method. The rest of the paper is organized as follows. In Section 2, we describe the extended (G'/G)-expansion method to seek travelling wave solutions of nonlinear evolution equations and give the main steps of the method. In Section 3, we illustrate the method in detail with the modified non-linear Schrodinger equation in deep water. In Section 4, some conclusions are given.
2. Description of the Extended (G'/G)-Expansion Method
In this section, we describe the main steps of the extended (G'/G)-expansion method for finding travelling wave solutions of nonlinear evolution equations.
Suppose that we have a nonlinear partial differential equation for 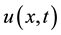 in the form:
in the form:
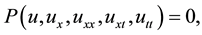 (1)
(1)
where 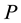 is a polynomial in its arguments. The essence of this approach can be formulated as follows:
is a polynomial in its arguments. The essence of this approach can be formulated as follows:
Step 1. Find travelling wave solutions of Equation (1) by taking 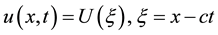 and transform Equation (1) to the ordinary differential equation:
and transform Equation (1) to the ordinary differential equation:
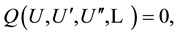 (2)
(2)
where prime denotes the derivative with respect to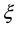 .
.
Step 2. If possible, integrate Equation (2) term by term one or more times. This yields constant(s) of integration. For simplicity, the integration constant(s) can be set to zero.
Step 3. Introduce the solution 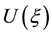 of Equation (2) in the finite series form:
of Equation (2) in the finite series form:
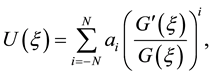 (3)
(3)
where 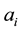 are real constants with
are real constants with 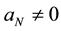 to be determine,
to be determine, 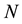 is a positive integer to be determined. The function
is a positive integer to be determined. The function  is the solution of auxiliary linear ordinary differential equation:
is the solution of auxiliary linear ordinary differential equation:
 (4)
(4)
where 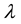 and
and 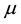 are real constants to be determined.
are real constants to be determined.
Step 4. Determine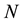 . This, usually, can be accomplished by balancing the linear term(s) of highest order with the highest order nonlinear term(s) in Equation (2).
. This, usually, can be accomplished by balancing the linear term(s) of highest order with the highest order nonlinear term(s) in Equation (2).
Step 5. Substitute (3) together with (4) into Equation (2) yields an algebraic set equation involving powers of






3. Application
Deep-water irrotational gravity waves propagating at the surface of an inviscid incompressible fluid are governed at third order in amplitude, by an equation first derived by Zakharov [38] :

where

The modified nonlinear Schrodinger equation [40] obtained from Equation (5) is given by:

where the different coefficient are given by:






and





an introduce a new variable :

Replacing Equation (14) into Equation (6), separating the real and imaginary part and using the relation (15) leads to a system of equations:


Now we make an ansatz (3) for the solution of Equations (16) and (17). By balancing the terms 






where 







Substituting these expressions into Equations (16) and (17), we collect and setting all terms of the same power of 



The ODE Equation (4) may then be solved exactly and admits the following solutions:



With:




where 

First type. Hyperbolic functions travelling wave solutions.
a) if 


Then:


If 


b) if 




Second type. Trigonometric functions travelling wave solutions.
c) if 


Then:


d) if 


Then:


Third type. Rational functions travelling wave solutions.
e) if

Then:


Hyperbolic and trigonometric solutions can also be express in the form [42] - [46] :

with

with
We are on deep water, the behavior of the ocean cant not be determine exactly. We don’t know the form that wave will takes. All cases are possible. The Figures 1-3 show the behavior of the exact solution of the modified nonlinear Schrödinger equation modeling the propagation of rogue waves in deep water for certain values of the system parameters. The squared modulus of the amplitude of the wave 


The snapshot of Figure 1 is a typical representation of one pulse-type solutions [47] , proof that the solutions thus obtained are general and take into account the solutions already existing in the open literature. When the system parameters vary, there is a sudden variation in the amplitude of wave Figure 2 and Figure 3. These results allow us to confirm the fact that the amplitudes of waves may vary in exceptional cases by simply changing a parameter of the system, take us with amplitude of one to over one hundred without any trial. These results re-
Figure 1. One pulse with low amplitude.






Figure 2. One pulse with large amplitude presented like a barrier.






Figure 3. One pulse with large amplitude presented like a giant saw.






flect very well the situation encountered by sailors in ocean: the free surface of a body of deep water just move from a situation of absolute calm to the appearance of a gigantic wall of water [48] . Figure 2 and Figure 3 are as gigantic barrier 2 have a regular summit while 3 has a peak saw tooth which allow us to conclude that in most cases, the tops of the waves is not regular. When these kinds of waves propagate at high speed and collided with a tanker or striking an oil platform, these structures will be send to the mat with frightening speed and efficiency. Freaks waves arise abruptly, when one of the form 2 or 3 surprises ships from below, it behaves like a giant saw, cutting steel look like a knife on the butter or breaks it in two because the cumulative effects of their considerable height and wavelength literally raised the ship from both ends. It central part is then in vacuum, or at least less driven by water and would then be subjected to enormous stresses.
4. Conclusion
In this paper, generalized extended (G'/G)-expansion method is used to obtain the exact solutions of modified nonlinear Schrödinger equation in deep water. Particular attentions have been paid to the amplitude of the found solutions and to the relationship between dynamics of these solutions and some characteristics of extreme abnormal sea wave with abnormal shape. The solutions are expressed in the form of hyperbolic functions, trigonometric functions and rational solutions from which some special solutions including the known solitary wave solution are derived by setting appropriate values for the parameter. Compared with other methodologies mentioned in introduction, this method is direct, concise, elementary and it can be implemented in more complicated nonlinear equations by using symbolic computations. One pulse with large amplitude presented like a barrier or like a giant saw are very dangerous for sailors, offshore oil platforms and coastal structures. The representation on this paper give partially the reasons of the damage caused on the hulls of super tankers when they collide with this crazy waves like that in Figure 4 and Figure 5.
Figure 4. Profile view of damage caused on energy endurance [49] .
Figure 5. The WILSTAR Norvegian cargo boat hit by a rogue waves [49] .
Acknowledgements
We are grateful to Conrad Bertrand TABI for useful discussions and for valuable comments on this work during it progression.
References
- Mallory, J.K. (1974) Abnormal Waves on the South-East of South Africa. International Hydrographic Review, 51, 89-129.
- Lavrenov, I. (1998) The Wave Energy Concentration at the Agulhas Current of South Africa. Natural Hazards, 17, 117-127. http://dx.doi.org/10.1023/A:1007978326982
- Lawton, G. (2001) Monters of the Deep (the Perfect Wave). New Scientist, 170, 28-32.
- Nikolkina, I. and Didenkulova, I. (2011) Rogue Waves in 2006-2010. Natural Hazards and Earth System Sciences, 11, 2913-2924. http://dx.doi.org/10.5194/nhess-11-2913-2011
- Rosenthal, W., Lehner, S., Dankert, H., Guenther, H., Hessner, K., Horstmann, J., Niedermeier, A., Nieto-Borger, J.C., Schulz Stellenfleth, J. and Reichert, K. (2003) Detection of Extreme Single Waves and Wave Statistics. In: Rogue Waves: Forecast and Impact on Marine Structures, GKSS Research Center, Geesthacht, Germany, Papers WP 1, 3.
- Lehner, S., Gunther, H. and Rosenthal, W. (2005) Extreme Wave Observations from Radar Data Sets, Ocean Waves Measurements and Analysis. 5th International Symposium, WAVES 2005, Madrid, 3-7 July 2005, Paper 69.
- Kharif, C. and Pelinovsky, E. (2003) Physical Mechanisms of the Rogue Wave Phenomenon. European Journal of Mechanics―B/Fluids, 22, 603-634.
- Dysthe, K., Krogstad, H.E. and Muller, P. (2008) Oceanic Rogue Waves. Annual Review of Fluid Mechanics, 40, 287- 310. http://dx.doi.org/10.1146/annurev.fluid.40.111406.102203
- Kharif, C., Pelinovsky, E. and Slunyaev, A. (2009) Rogue Waves in the Ocean. Springer Verlag, Berlin.
- Gramstad, O. and Trulsen, K. (2007) Influence of Crest and Group Length on the Occurrence of Freak Waves. Journal of Fluid Mechanics, 582, 463-472. http://dx.doi.org/10.1017/S0022112007006507
- Mori, N., Liu, P.C. and Yasuda, T. (2002) Analysis of Freak Wave Measurements in the Sea of Japan. Ocean Enginee- ring, 29, 1399-1414. http://dx.doi.org/10.1016/S0029-8018(01)00073-7
- Onorato, M., Osborne, A.R., Serio, M. and Cavaleri, L. (2005) Modulational Instability and Non-Gaussian Statistics in Experimental Random Water-Wave Trains. Physics of Fluids, 17, Article ID: 078101. http://dx.doi.org/10.1063/1.1946769
- Onorato, M., Waseda, T., Toffoli, A., Cavaleri, L., Gramstad, O., Janssen, P.A.E.M., Kinoshita, T., Monbaliu, J., Mori, N., Osborne, A.R., Serio, M., Stansberg, C., Tamura, H. and Trulsen, K. (2009) Statistical Properties of Directional Ocean Waves: The Role of the Modulational Instability in the Formation of Extreme Events. Physical Review Letters, 102, Article ID: 114502. http://dx.doi.org/10.1103/PhysRevLett.102.114502
- Socquet-Juglard, H., Dysthe, K., Trulsen, K., Krogstad, H. and Liu, J. (2005) Distribution of Surface Gravity Waves during Spectral Changes. Journal of Fluid Mechanics, 542, 195-216.
- Tamura, H., Waseda, T. and Miyazawa, Y. (2009) Freakish Sea State and Swell-Windsea Coupling: Numerical Study of the Suwa-Maru Incident. Geophysical Research Letters, 36. http://dx.doi.org/10.1029/2008GL036280
- Toffoli, A., Onorato, M., Babanin, A.V., Bitner-Gregersen, E., Osborne, A.R., Monbaliu, J., et al. (2007) Second-Order Theory and Setup in Surface Gravity Waves: A Comparison with Experimental Data. Journal of Physical Oceanography, 37, 2726-2739. http://dx.doi.org/10.1175/2007JPO3634.1
- Toffoli, A., Gramstad, O., Trulsen, K., Monbaliu, J., Bitner-Gregersen, E.M. and Onorato, M. (2010) Evolution of Weakly Nonlinear Random Directional Waves: Laboratory Experiments and Numerical Simulations. Journal of Fluid Mechanics, 664, 313-336. http://dx.doi.org/10.1017/S002211201000385X
- Waseda, T., Kinoshita, T. and Tamura, H. (2009) Evolution of a Random Directional Wave and Freak Wave Occurrence. Journal of Physical Oceanography, 39, 621-639. http://dx.doi.org/10.1175/2008JPO4031.1
- Waseda, T., Hallerstig, M., Ozaki, K. and Tomita, H. (2011) Enhanced Freak Wave Occurrence with Narrow Directional Spectrum in the North Sea. Geophysical Research Letters, 38. http://dx.doi.org/10.1029/2011GL047779
- Lechuga, A. (2012) Generation of Rogue Waves in a Wave Tank. Geophysical Research Abstracts, 14, 1.
- Lechuga, A. (2013) Rogue Waves in a Wave Tank: Experiments and Modeling. Natural Hazards and Earth System Sciences, 13, 2951-2955. http://dx.doi.org/10.5194/nhess-13-2951-2013
- Nwatchok, S.A.A., Biouele, C.M., Zobo, B.E. and Nkomom, T.N. (2011) Application of Zakharov Equation in Three Dimensions to Deep Water Gravity Waves. International Journal of the Physical Sciences, 6, 7447-7455.
- Zakharov, V. and Ostrovsky, L. (2009) Modulation Instability: The Beginning. Physica D: Nonlinear Phenomena, 238, 540-548. http://dx.doi.org/10.1016/j.physd.2008.12.002
- Osborne, A.R. (2010) Nonlinear Ocean Waves and the Inverse Scattering Transform. International Geophysics Series, Elsevier, San Diego.
- Onorato, M., Osborne, A., Serio, M., Cavaleri, L., Brandini, C. and Stansberg, C. (2006) Extreme Waves, Modulational Instability and Second Order Theory: Wave Flume Experiments on Irregular Waves. European Journal of Mechanics, B/Fluids, 25, 586-601. http://dx.doi.org/10.1016/j.euromechflu.2006.01.002
- Toffoli, A., Onorato, M., Bitner-Gregersen, E., Osborne, A.R. and Babanin, A.V. (2008) Surface Gravity Waves from Direct Numerical Simulations of the Euler Equations: A Comparison with Second-Order Theory. Ocean Engineering, 35, 367-379. http://dx.doi.org/10.1016/j.oceaneng.2007.10.004
- Zakharov, V.E., Dyachenko, A.I. and Shamin, R.V. (2010) How Probability for Freak Wave Formation Can Be Found. The European Physical Journal Special Topics, 185, 113-124. http://dx.doi.org/10.1140/epjst/e2010-01242-y
- Bitner-Gregersen, E.M. and Toffoli, A. (2012) On the Probability of Occurrence of Rogue Waves. Natural Hazards and Earth System Sciences, 12, 751-762.
- Akhmediev, N., Eleonskii, V.Z. and Kulagin, N. (1985) Generation of Periodic Trains of Picosecond Pulses in an Optical Fiber: Exact Solutions. Soviet Physics, JETP, 62, 894-899.
- Akhmediev, N., Ankiewicz, A. and Soto-Crespo, J.M. (2009) Rogue Waves and Rational Solutions of the Nonlinear Schrödinger Equation. Physical Review E, 80, Article ID: 026601. http://dx.doi.org/10.1103/PhysRevE.80.026601
- Akhmediev, N., Ankiewicz, A. and Taki, M. (2009) Waves That Appear from Nowhere and Disappear without a Trace. Physical Letters A, 373, 675-678. http://dx.doi.org/10.1016/j.physleta.2008.12.036
- Akhmediev, N., Soto-Crespo, J.M. and Ankiewicz, A. (2009) Extreme Waves That Appear from Nowhere: On the Nature of Rogue Waves. Physical Letters A, 373, 2137-2145. http://dx.doi.org/10.1016/j.physleta.2009.04.023
- Wang, M., Li, X. and Zhang, J. (2008) The (G’/G)-Expansion Method and Traveling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics. Physical Letters A, 372, 417-423.
- Bekir, A. (2008) Application of the (G’/G)-Expansion Method for Nonlinear Evolution Equations. Physical Letters A, 372, 3400-3406. http://dx.doi.org/10.1016/j.physleta.2008.01.057
- Zedan, H.A. (2010) New Classes of Solutions for a System of Partial Differential Equations by (G’/G)-Expansion Method. Nonlinear Science Letters A, 1, 219-238.
- Zhang, J., Wei, X. and Lu, Y. (2008) A Generalized (G’/G)-Expansion Method and Its Applications. Physical Letters A, 372, 3653-3658. http://dx.doi.org/10.1016/j.physleta.2008.02.027
- Zayed, E.M.E. and Gepreel, K.A. (2009) The (G’/G)-Expansion Method for Finding Traveling Wave Solutions of Nonlinear Partial Differential Equations in Mathematical Physics. Journal of Mathematical Physics, 50, Article ID: 013502. http://dx.doi.org/10.1063/1.3033750
- Zakharov, V.E. (1968) Stability of Periodic Waves of Finite Amplitude on the Surface of Deep Fluid. Journal of Applied Mechanics and Technical Physics, 2, 190-194.
- Krasitskii, V.P. (1994) On Reduced Equations in the Hamiltonian Theory of Weakly Nonlinear Surface Waves. Journal of Fluid Mechanics, 272, 1-20. http://dx.doi.org/10.1017/S0022112094004350
- Stiassnie, M. (1984) Note on the Modified Nonlinear Schrodinger Equation for Deep Water Wave. Wave Motion, 6, 431-433. http://dx.doi.org/10.1016/0165-2125(84)90043-X
- El-Wakil, S.A., Abdou, M.A. and Hendi, A. (2008) New Periodic Wave Solutions via Exp-Function Method. Physics Letters A, 372, 830-840. http://dx.doi.org/10.1016/j.physleta.2007.08.033
- Demiray, H. (2009) Variable Coefficient Modified KdV Equation in Fluid-Filled Elastic Tubes with Stenosis: Solitary Waves. Chaos Solitons Fractals, 42, 358-364. http://dx.doi.org/10.1016/j.chaos.2008.12.014
- Zhang, S., Dong, L., Ba, J.M. and Sun, Y.N. (2010) The (G’/G)-Expansion Method for a Discrete Nonlinear Schrö- dinger Equation. Pramana, 74, 207-218.
- Arora, R. and Yadav, S. (2012) The (G’/G)-Expansion Method for Traveling Wave Solutions of Burgers’ Kdv and Ge- neralization of Huxley Equations. American Journal of Computational and Applied Mathematics, 2, 119-123. http://dx.doi.org/10.5923/j.ajcam.20120203.09
- Li, L.X. and Wand, M.L. (2009) The (G’/G)-Expansion Method and Travelling Wave Solutions for a Higher-Order Nonlinear Schrödinger Equation. Applied Mathematics and Computation, 208, 440-445. http://dx.doi.org/10.1016/j.amc.2008.12.005
- Kheiri, H., Moghaddam, M.R. and Vafaei, V. (2011) Application of the (G’/G)-Expansion Method for the Burgers, Burgers-Huxley and Modified Burgers-Kdv Equations. Pramana, 76, 831-842.
- Hacinliyan, I. and Erbay, S. (2004) Coupled Quintic Nonlinear Schrodinger Equations in a Generalized Elastic Solid. Journal of Physics A: Mathematical and General, 37, 9387-9401
- Müller, P., Garrett, C. and Osborne, A. (2005) Meeting Report: Rogue Waves―The Fourteenth ’Aha Huliko’a Hawai- ian Winter Workshop. Oceanography, 18, 66-75. http://dx.doi.org/10.5670/oceanog.2005.30
- Energy Endurance. www.lethist.laure.net/Scelerates.htm
NOTES
*Corresponding author.









