Open Journal of Genetics
Vol.09 No.01(2019), Article ID:91470,15 pages
10.4236/ojgen.2019.91002
Assessing Likelihood of Having False Positives Caused by Population Stratification
Renfang Jiang, Jianping Dong
Department of Mathematical Sciences, Michigan Technological University, Houghton, USA

Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 1, 2019; Accepted: March 25, 2019; Published: March 28, 2019
ABSTRACT
Population stratification is always a concern in association analysis. There is a debate on the extent of the problem in less extreme situations (Thomas and Witte [1] , Wacholder et al. [2] ). Wacholder et al. [3] and Ardlie et al. [4] showed that hidden population structure is not a serious threat to case-control designs. We propose a method of assessing the seriousness of the population stratification before designing association studies. If population stratification is not a serious problem, one may consider using case-control study instead of family-based design to get more power. In a case-control design, we compare chi-square statistics from a structured population (a union of two subpopulations) and a homogeneous population with the same prevalence and allele frequencies. We provide an explicit formula to calculate the chi-square statistics from 17 parameters, such as proportions of subpopulation, allele frequencies in subpopulations, etc. We choose these factors because they have potential to cause false associations. Each parameter takes a random value in a chosen range. We then calculate the likelihood of getting opposite conclusions in the structured and the homogeneous populations. This is the likelihood of having false positives caused by population stratification. The advantage of this method is to provide a cost effective way to choose between using case-control data and using family data before actually collecting those data. We conclude that sample sizes have a significant effect on the likelihood of false positive caused by population stratification. The larger the sample size is, the more likely to have false positive if the population structure is ignored. If the sample size will be smaller than 200 by budget constraints, then case-control study may be a better choice because of its power.
Keywords:
Population Stratification, Case-Control Studies, Linkage Disequilibrium, Genome-Wide Association Studies

1. Introduction
After Human Genome Project, the studies of genetic variation in human population have been developed extensively [5] [6] . Genome-wide association study has become a major tool in identifying genetic variants associated with disease risk. It is well documented that case-control samples from non-homogeneous populations could cause bias in association measures [1] . Therefore, population stratification is always a serious concern in association analysis [7] [8] . When a candidate gene shows a positive association with a disease, one always wonders whether the gene is truly responsible for the disease, or it is merely more common in a subpopulation that is more likely to suffer from the disease [9] . Thomas and Witte [1] gave a good summary about the problem. To avoid this problem, many family-based methods were proposed, which includes TDT (Spielman et al. [10] ) and its extensions. Devlin and Roeder [11] and Pritchard and Rosenberg [12] proposed to test population stratification by using unlinked markers. Shin and Lee [13] proposed a mixed model to reduce spurious genetic associations produced by population stratification in genome-wide association studies. One way to detect stratification is to compute the genomic control [14] . Some programs have been developed for inferring genetic ancestry [15] . Principal component analysis has also been used in adjusting for confounding due to population stratification in DNA methylation studies [16] . Some studies have been conducted to explore associations between some common SNPs and social deprivation measure of socio-economic status, which have to deal with structured population data [17] .
Wacholder et al. [2] argued that the population stratification is not a serious threat to the reliability of cohort and case-control studies. Wacholder et al. [3] showed that ignoring ethnicity among non-Hispanic U.S. Caucasians only causes a small bias: sometimes less than one percent and almost always less than ten percent. This example shows that population stratification does not always cause significant bias.
Ardlie et al. [4] tested hidden population structures in four case-control samples, US whites and African Americans with hypertension, US whites and Polish whites with type 2 diabetes. They found weak evidence in African American sample only. The study conducted by Pankow et al. [18] provided further evidence that the population stratification is not a serious threat to case-control studies.
If population stratification is a serious problem, the reliability of case-control studies will be doubtful, and any positive results from case-control studies have to be reconfirmed by studies based on family-member controls. On the other hand, if this is not a serious problem, we do not have to spend valuable resources on collecting family-based data to just prevent bias caused by population stratification. Many people believe that case-control study is more powerful than family-based study (Morton and Collins [19] , Bacanu et al. [20] , Spence et al. [21] ). Therefore, it is desirable to have a method to assess the seriousness of the population stratification before designing association studies. There is no doubt that population stratification will cause bias. It is also agreed that population stratification is caused by variations in allele frequencies and disease risks across subpopulations (Thomas and Witte [1] , Wacholder et al. [2] ). It is unclear when this bias will be big enough to change the conclusion of the association study.
In this paper we propose a method to assess the seriousness of population stratification. In order to quantitatively study the bias caused by population stratification, we consider two populations that have exactly the same marker allele frequencies, the same disease gene frequencies, and the same penetrance. Nevertheless, one population is structured (denoted as Population I) and the other is homogeneous (denoted as Population II). Seventeen factors in a population are analyzed. We choose these factors because they have potential to cause false associations. In a case-control design, at a biallelic marker, a standard chi-square statistic is used to test the association between the marker locus and an unknown disease locus. We want to know when data from the structured population and the homogeneous population yield different conclusions. Namely, we want to know when we will get a false positive (or a false negative) by neglecting the population structure. Our approach is to calculate the chi-square statistic from 17 parameters. We will randomly choose each parameter within its range, and then compare the chi-square statistics for the structured and the homogeneous populations. The percentage of false conclusions (positive or negative) will be recorded. This is the likelihood of the false conclusion caused by population stratification. The key step in our approach is an explicit formula for calculating marker allele frequencies among affected people and among normal people. This formula is given in Section 4. Since the rate of false positive depends on the ranges we have chosen for the parameters, we write the explicit formula in a computer program, in which the ranges of all parameters can be chosen by the user, and the program will calculate the likelihood of the false conclusion caused by population stratification under the chosen circumstance.
We will use the following notations:
1) I: population I (structured), which consists of two homogeneous subpopulations 1 and 2.
2) II: population II (homogeneous).
3) 1: subpopulation 1.
4) 2: subpopulation 2.
5) D: diseased people.
6) N: normal people.
7) M: a marker allele.
8. A: a disease allele.
9) , : prevalence, which is the likelihood of getting affected given genotype , , AA, respectively.
10) : probability.
2. Methods
Population I is a union of two homogeneous subpopulations, and there is no admixture. The reason we choose two subpopulations instead of three or more is the general belief that the effect of population stratification will decrease as the number of subpopulations increases, and we want to consider the worst case scenario. We will compare population I (structured) with population II (homogeneous). In order to compare populations I and II, they have to have something in common. We assume that they have the same allele frequencies and penetrance.
In a case-control design, consider a biallelic marker locus with alleles M and . Suppose allele M appears more often in cases than in controls. Suppose the disease is caused by an unknown disease gene with several disease alleles and a normal allele . We assume that the disease alleles were introduced into the general population at different time, and there were multiple ancestral haplotypes. Suppose the disease allele was introduced into the general population generations ago. Let be a lower bound of the age of the latest mutant disease allele. Suppose n generations ago, the conditional probability of a chromosome having allele M given it has is . Note that the unknown ages of mutant disease alleles are absorbed into the unknown incomplete initial association, and they do not cause additional troubles. Suppose that are functionally equivalent disease alleles, i.e. the penetrance is for , for , and , where D indicates the disease phenotype. Letting , then . For population I, we look at Table 1, where are the number of times that allele appears in the group. For example, suppose that the sample contains 100 affected people, among which 20 with genotype MM, and 50 with genotype . Then . For population II, is replaced by . The chi-square statistics are
and are chi-square statistics with one degree freedom for population I and II, respectively. Consider a sample with cases and controls. Instead of taking a random sample, we calculate and using the following formula, where D and N indicate diseased and normal, and I and II indicate populations I and II.
Table 1. A case-control study.
Note that depends on and , and depends on and . These conditional probabilities , , , and depend on 17 parameters. We will give an explicit formula in (7)-(10) for calculating these conditional probabilities when given values of the parameters. The parameters are as follows:
1) is the proportion of subpopulation 1.
2) is the proportion of subpopulation 2.
3) is the frequency of marker allele M in subpopulation 1.
4) is the frequency of marker allele M in subpopulation 2.
5) is the frequency of disease allele A in subpopulation 1.
6) is the frequency of disease allele A in subpopulation 2.
7) n is a lower bound of the age of the latest mutant disease allele.
8) is the genetic distance between marker locus and the disease gene.
9) is the number of cases, and it is also the number of controls.
10) is the likelihood of getting affected in subpopulation 1 given genotype .
11) is the likelihood of getting affected in subpopulation 1 given genotype .
12) is the likelihood of getting affected in subpopulation 1 given genotype AA.
13) is the likelihood of getting affected in subpopulation 2 given genotype .
14) is the likelihood of getting affected in subpopulation 2 given genotype .
15) is the likelihood of getting affected in subpopulation 2 given genotype AA.
16) is the association between M and A in population 1, n generations ago.
17) is the association between M and A in population 2, n generations ago.
Populations I and II have the same allele frequencies and the same penetrance:
(1)
(2)
We also assume that, n generations ago, populations I and II have the same initial association between the marker allele M and the disease allele A, which is
(3)
3. Results
We now calculate the likelihood of false conclusion caused by population stratification in different circumstances. We first choose the ranges for the parameters. Each parameter is chosen randomly in the range. For each set of the parameters, we can calculate chi-square statistics and for structured population I and the homogeneous population II. At 5% level, if and are at the different sides of 3.8414, i.e. either or , we then call it a false conclusion (a false positive, or a false negative). This means that at 5% level, if we treat the structured population as a homogeneous population (ignoring the subpopulation structure), then we get a wrong conclusion. We then record the percentage of false conclusions. We will do the same thing at 1% level, instead of 3.8414 we will use 6.6345. The ranges of the parameters are the following:
Circumstance 1.
1) , .
2) , .
3) , .
4) .
5) (in cM).
6) .
7) , .
8) , .
One million simulations have been run, and the rate of having different conclusions in populations I and II has been recorded, which is called the false rate.
The false rate is 4.84% at 5% significance level; and it is 2.25% at the 1% significance level, and it is 0.93% at the 0.1% significance level. The simulations have been run for ten million times as well, and the results are 4.82%, 2.27%, and 0.94%, respectively. So running one million times is accurate enough. The above ranges are so wide that we can say that in a case-control study using 100 cases and 100 controls, the possibility of getting a false positive caused by ignoring unknown population structure is small.
Next, we want to investigate the effect of each parameter on the false rate.
Note that in Circumstance 1, the maximum possible ratio of marker allele frequencies in two subpopulations is 9. From Table 2 we can see that if we allow this maximum ratio to increase, the false rates will increase accordingly. If the maximum ratio is 99 instead of 9, the false rate will be doubled. From Table 3 we can see the effect of changing ranges of disease allele frequencies on the false rates. The results are similar to those in Table 2. If we change the ranges of frequencies of both marker and disease alleles, the combined effect is larger (see Table 4). But they are still within 10%.
The disease models and penetrance are difficult to estimate in practice. From Table 5, their effects on the false rate are not big.
The genetic distance between the marker and the disease gene is of cause unknown. From Table 6, its value does not make big difference on the false rate. The worst case occurs when the marker is at the disease locus, which is not a false positive.
The age of the latest disease mutation and the initial association between marker allele and the disease allele are hard to estimate. From Table 7 & Table 8, their effects on the false rate are minimum.
Table 2. The false rates. The ranges of marker allele frequencies are changed, everything else is the same as in Circumstance 1.
Table 3. The false rates. The ranges of the disease allele frequencies are changed, every thing else is the same as in Circumstance 1.
Table 4. The false rates. The ranges of the disease allele frequencies AND marker allele frequencies are changed, every thing else is the same as in Circumstance 1.
Table 5. The false rates. The ranges of the disease penetrance are changed, every thing else is the same as in Circumstance 1.
Table 6. The false rates. The recombination fraction is changed, every thing else is the same as in Circumstance 1.
Table 7. The false rates. The age of the disease mutation is changed, every thing else is the same as in Circumstance 1.
Table 8. The false rates. The ranges of the initial association are changed, every thing else is the same as in Circumstance 1.
The proportion of a subpopulation in the whole population is an important factor affecting the false rate. From Table 9, the false rate increases 8 times as the
proportion changes from 10% to 50%. The worst case occurs when the whole population is a union of two equal parts. If only a small part of the sample is from a different population (for example 10%), the chance of having a false positive is small.
A surprising result comes from Table 10: the false rate increases as sample size increases. We offer a possible explanation: if the sample size is small, the bias caused by population stratification is buried among other larger noises; if the sample size is large, the bias caused by population stratification becomes a significant factor. This phenomenon needs further study.
4. The Explicit Formula for Calculating Marker Allele Frequencies among Affected People and among Normal People
We will give an explicit formula for allele frequencies among cases and controls in populations I and II. The frequencies of marker allele and disease allele in population I are
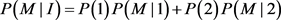
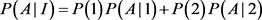
The penetrance in population I are
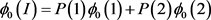
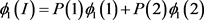
Two subpopulations 1 and 2, and population II are assumed to be homogeneous. Therefore, Hardy-Weinberg equilibrium holds. The disease prevalence in these population can be calculated as follows:
Table 9. The false rates. The proportion of a subpopulation is changed, every thing else is the same as in Circumstance 1.
Table 10. The false rates. The sample size is changed, every thing else is the same as in Circumstance 1.
Since population I is not homogeneous, Hardy-Weinberg equilibrium does not hold. In particular, the disease prevalence in population I cannot be calculated as above.
Next, we will calculate the frequency of marker allele M among cases in a homogeneous population, for example subpopulations 1 and 2, and population II. Since the argument holds for all three populations, we will not specify the population. Let





We now consider an ordered pair of haplotypes. Let 



Similarly,
Then

where
Next, we calculate









We will calculate the frequency of haplotype 



where 
We then have

Substituting (6) into (4) and (5) yields the frequencies of allele M among cases and controls in population II:


where







We now calculate the frequency of allele M among cases and controls in population I (the structured population). Since population I is not homogeneous, Hardy-Weinberg equilibrium does not hold. We cannot use the above formula. Instead we have the following:
Note that
We then have


where
5. Discussion
We provide a formula for calculating the likelihood of false positive caused by population stratification given the ranges of the parameters. This is written in a computer program. From Tables 2-10 we can see that without any knowledge about the structure of the population (i.e. each parameter has a wide range of possibilities), the chance of getting false positives from ignoring the population structure is small. Sample sizes have a significant effect on the likelihood of false positive caused by population stratification. The larger the sample size is, the more likely to have false positive if the population structure is ignored. For small samples (the sum of numbers of cases and controls is smaller than 200), when unknown population structure is ignored, the chance of having false positive is less than 5%. We suggest using sample size as a factor in choosing study design (case-control or family-based), if the sample size will be smaller than 200 by budget constraints, then case-control study may be a better choice because of its power. Of cause, cases and controls should be carefully matched. If there are still some unknown population differences between cases and controls, the chance of having false positive caused by unknown population structure is less than 5%.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
References
- 1. Thomas, D.C. and Witte, J.S. (2002) Point: Population Stratification: A Problem for Case-Control Studies of Candidate-Gene Associations? Cancer Epedemiology, Biomarkers & Prevention, 11, 505-512.
- 2. Wacholder, S., Rothman, N. and Caporaso, N. (2002) Counterpoint: Bias from Population Stratification Is Not a Major Threat to the Validity of Conclusions from Epidemiological Studies of Common Polymorphisms and Cancer. Cancer Epidemiology, Biomarkers & Prevention 11, 513-520.
- 3. Wacholder, S., Rothman, N. and Caporaso, N. (2000) Population Stratification in Epidemiologic Studies of Common Genetic Variants and Cancer: Quantification of Bias. Journal of the National Cancer Institute, 92, 1151-1158. https://doi.org/10.1093/jnci/92.14.1151
- 4. Ardlie, K.G., Lunetta, K.L. and Seielstad, M. (2002) Testing for Population Subdivision and Association in Four Case-Control Studies. American Journal of Human Genetics, 71, 304-311. https://doi.org/10.1086/341719
- 5. Visscher, P.M., et al. (2017) 10 Years of GWAS Discovery: Biology, Function, and Translation. American Journal of Human Genetics, 101, 5-22. https://doi.org/10.1016/j.ajhg.2017.06.005
- 6. Oetjens, M.T. (2016) Population Stratification in the Context of Diverse Epidemiologic Surveys Sans Genome-Wide Data. Frontiers in Genetics, 7, 76. https://doi.org/10.3389/fgene.2016.00076
- 7. Cardon, L.R. and Palmer, L.J. (2003) Population Stratification and Spurious Allelic Association. The Lancet, 361, 598-604. https://doi.org/10.1016/S0140-6736(03)12520-2
- 8. Hellwege, J., et al. (2018) Population Stratification in Genetic Association Studies. Current Protocols in Human Genetics, 95, 1.22.1-1.22.23.
- 9. Ali-Khan, S.E., et al. (2011) The Use of Race, Ethnicity and Ancestry in Human Genetic Research. The HUGO Journal, 5, 47-63. https://doi.org/10.1007/s11568-011-9154-5
- 10. Spielman, R.S., McGinnis, R.E. and Ewens, W.J. (1993) The Transmission Test for Linkage Disequilibrium: The Insulin Gene and Insulin-Dependent Diabetes Mellitus (IDDM). American Journal of Human Genetics, 52, 506-516.
- 11. Devlin, B. and Roeder, K. (1999) Genomic Control for Association Studies. Biometrics, 55, 997-1004. https://doi.org/10.1111/j.0006-341X.1999.00997.x
- 12. Pritchard, J.K. and Rosenberg, N.A. (1999) Use of Unlinked Genetic Markers to Detect Population Stratification in Association Studies. American Journal of Human Genetics, 65, 220-228. https://doi.org/10.1086/302449
- 13. Shin, J. and Lee, C. (2015) A Mixed Model Reduces Spurious Genetic Associations Produced by Population Stratification in Genome-Wide Association Studies. Genomics, 105, 191-196. https://doi.org/10.1016/j.ygeno.2015.01.006
- 14. Price, A.L., Zaitlen, N.A., Reich, D. and Patterson, N. (2010) New Approaches to Population Stratification in Genome-Wide Association Studies. Nature Reviews Genetics, 11, 459-463. https://doi.org/10.1038/nrg2813
- 15. Alexander, D.H., Novembre, J. and Lange, K. (2009) Fast Model-Based Estimation of Ancestry in Unrelated Individuals. Genome Research, 19, 1655-1664. https://doi.org/10.1101/gr.094052.109
- 16. Barfield, R.T., et al. (2014) Accounting for Population Stratification in DNA Methylation Studies. Genetic Epidemiology, 38, 231-241. https://doi.org/10.1002/gepi.21789
- 17. Hill, W.D., et al. (2016) Molecular Genetic Contributions to Social Deprivation and Household Income in UK Biobank. Current Biology, 26, 3083-3089. https://doi.org/10.1016/j.cub.2016.09.035
- 18. Pankow, J.S., Province, M.A., Hunt, S.C. and Arnett, D.K. (2002) Regarding “Testing for population Subdivision and Association in Four Case-Control Studies”. American Journal of Human Genetics, 71, 1478-1480. https://doi.org/10.1086/344582
- 19. Morton, N.E. and Collins, A. (1998) Tests and Estimates of Allelic Association in Complex Inheritance. Proceedings of the National Academy of Sciences of the United States of America, 95, 11389-11393. https://doi.org/10.1073/pnas.95.19.11389
- 20. Bacanu, S.A., Devlin, B. and Roeder, K. (2000) The Power of Genomic Control. American Journal of Human Genetics, 66, 1933-1944. https://doi.org/10.1086/302929
- 21. Spence, M.A., Greenberg, D.A., Hodge, S.E. and Vieland, V.J. (2003) The Emperor’s New Methods. American Journal of Human Genetics, 72, 1084-1087. https://doi.org/10.1086/374826
- 22. Hartl, D.L. (1999) A Primer of Population Genetics. 3rd Edition, Sinauer, Sunderland, MA.


























