Journal of Quantum Information Science
Vol.07 No.01(2017), Article ID:74833,29 pages
10.4236/jqis.2017.71002
The Approximation of Bosonic System by Fermion in Quantum Cellular Automaton
Shinji Hamada1, Hideo Sekino1,2,3
1Toyohashi University of Technology, Toyohashi, Japan
2Stony Brook University, New York, USA
3Tokyo Institute of Technology, Tokyo, Japan
Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 7, 2016; Accepted: March 19, 2017; Published: March 22, 2017
ABSTRACT
In one-dimensional multiparticle Quantum Cellular Automaton (QCA), the approximation of the bosonic system by fermion (boson-fermion correspondence) can be derived in a rather simple and intriguing way, where the principle to impose zero-derivative boundary conditions of one-particle QCA is also analogously used in particle-exchange boundary conditions. As a clear cut demonstration of this approximation, we calculate the ground state of few-particle systems in a box using imaginary time evolution simulation in 2nd quantization form as well as in 1st quantization form. Moreover in this 2nd quantized form of QCA calculation, we use Time Evolving Block Decimation (TEBD) algorithm. We present this demonstration to emphasize that the TEBD is most naturally regarded as an approximation method to the 2nd quantized form of QCA.
Keywords:
Quantum Cellular Automaton, QCA, Quantum Walk, Boson-Fermion Correspondence, Time Evolving Block Decimation, TEBD, Dirac Cellular Automaton

1. Introduction
Quantum Cellular Automaton (QCA) [1] is a quantum version of (classical) cellular automaton (CA). The word QCA was introduced by Grössing and Zeilinger [2] . But their model was not completely unitary. The QCA in the right meaning which has both locality and unitarity, was firstly investigated by Meyer [3] [4] [5] [6] , then followed by Boghosian and Taylor [7] [8] , though they used the term Quantum lattice gas automata (QLGA) for the two-component case. Since the middle of the 2000 s, new axiomatic approaches of QCA different from previous conventional or ad hoc ones have been proposed by several researchers [9] [10] [11] in order to comprehend QCA in more systematic and unified way by clarifying the definitions and/or to cope with the difficulties for extending it in a form relevant to the infinite dimensional Hilbert space. In most axiomatic QCAs, the unitarity and the causality (namely the existence of the upper limit on the speed of the information propagation) are fundamental and the locality is derived from them [10] . In this study, however, we describe QCA in a rather conventional fashion. There are several frameworks for quantum lattice systems other than QCA, namely Quantum Walk (QW) [12] , Quantum Lattice Gas Automata (QLGA) [7] [8] and Quantum Lattice Boltzmann (QLB) [13] . They are similar or mathematically equivalent to some QCAs [14] [15] . As QW and QLGA are thought to be subclasses of QCA [16] , we use the term QCA if at all possible.
QCA can be regarded as a discrete mechanical system with a simple and elegant time evolution rule. Though it is simple, it is not just a toy method. It can simulate the real quantum system of matter. Moreover there are several ideas that QCA plays a key role in fundamental physics [17] [18] and extensions to nonlinear QCA have been studied [19] which might be clues to constructing some class of interacting multiparticle QCA models.
QCA can be also regarded as one of the approximation methods for solving the continuous Time Dependent Schrödinger Equation (TDSE) like Finite Difference Method (FDM). However QCA is unique in that it preserves the complete unitarity of quantum systems upon its time progression and it can be regarded as the discrete version of direct solution for quantum dynamics, not merely an approximation to the TDSE. TDSE emerges rather as an approximation in the zero wavenumber limit of the general QCA solution. By extending the one-particle QCA to many-particle QCA, we explore the possibility of the method in real quantum systems.
The Time Evolving Block Decimation (TEBD) [20] [21] is one of the most successful methods to simulate quantum many-body systems. We however emphasize that it can be regarded as an approximation to the 2nd quantized form of QCA. In this study, we discuss the TEBD from the QCA point of view.
Since the success of Density Matrix Renormalization Group (DMRG) [22] , Matrix Product State (MPS) has been recognized as an efficient mathematical means for describing (quasi) one dimensional quantum many-body systems. The MPS is used both in eigenstate search by imaginary time evolution and in real time evolution of general states. TEBD is one of the standard algorithms in imaginary or real time evolution of MPS. The first part of TEBD algorism is to divide the Hamiltonian into even part and odd part, then the split-step or Suzuki-Trotter formalism is applied, namely the exponential of the even part or that of the odd part is applied alternatively to the 2nd quantized wavefunction. When we use the usual hopping term in the Hamiltonian as the kinetic energy part, this first part of TEBD can be regarded as 2nd quantized form of QCA. This QCA form seems to be a byproduct of the 2nd order Suzuki-Trotter decomposition or just an approximation method to the TDSE. In this study we however emphasize that it is more natural or fundamental to regard the one-particle QCA as the starting point of TEBD algorism in order to directly obtain the solution for general quantum systems.
The boson-fermion correspondence in the one dimensional quantum system is well known. However in studying QCA-TEBD formalism we notice that this can be derived in a rather simple and intriguing way. The main purpose of this study is to show this simple derivation and application to few body systems of boson. Numerical studies on applicable range of the “boson approximation” (approximation of the bosonic system by fermion) are also performed.
2. First Quantized Form of QCA
2.1. One-Particle QCA
Consider the simplest partitioned QCA on a 1D-time 1D-space lattice of which time evolution rule is given by Figure 1 and Equation (1) (for TDSE-type QCA). This rule is governed by the 2 ´ 2 basic unitary matrix (which is called scattering unitary matrix [11] ) which operates on a vector consisting of functions at adjacent grid points.
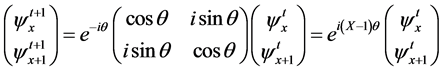 (1)
(1)
Here 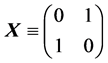 is the x-component of Pauli matrices and
is the x-component of Pauli matrices and .
. 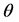
is the parameter of the TDSE-type QCA.
Though it is not straightforward to recognize intuitively, QCA gives a solution of the free particle TDSE in the zero wave number limit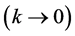 .
.
Figure 1. Evolution rule of QCA: The unit system where grid spacing 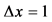 and time step
and time step 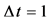 is used.
is used.
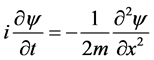 (2)
(2)
The relation between mass 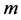 and
and  (the parameter of TDSE-type QCA) is given by
(the parameter of TDSE-type QCA) is given by
 (3)
(3)
This relation can be obtained by several methods as we will mention later. We introduce a simple derivation using FDM for small  as follows.
as follows.
By replacing the spatial derivative with the spatial difference, Equation (2) becomes
 (4)
(4)
Here 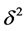 is the 2nd order central difference operator defined by
is the 2nd order central difference operator defined by
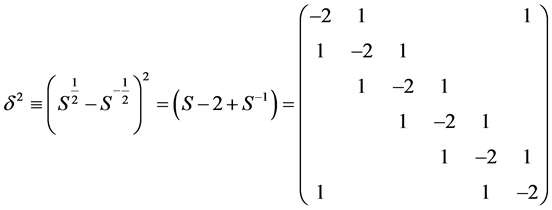 (5)
(5)
where S is the one-grid shift operator
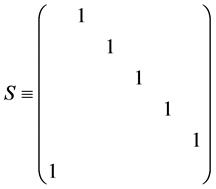 (6)
(6)
(Here we use 6 ´ 6 matrices assuming that the system consists of 6-grid points with periodic boundary condition. Moreover unfilled matrix elements are assumed to be zero throughout this article.)
Therefore the time evolution for the time step 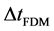 is given by
is given by

This 




where
Then 

Note that as 

divided into two steps ,so we naturally define 


ponds to Equation (3) for small
The QCA dynamics obeys such a simple rule above. However it requires more elaborate techniques to derive the exact relation between mass and QCA parameter 
There are several approaches to obtain the continuous limit (namely PDE) of QCA. The most naive and straightforward one is to connect the discrete time to continuous time by the interpolation and then to take a wavenumber (k) expansion around k = 0 in the spatial direction [23] [24] [25] . Although this approach lacks some exactness, it is sufficient to obtain right TDSE characteristics. More precise approach is to use a single scaling parameter 




not get into detailed derivation leading to the Dirac equation, as we are interested here in nonrelativistic case, though we will discuss a relevant topic in the last supplementary section.
2.2. Boundary Condition for QCA
There are basically three easily implementable boundary conditions for QCA. These are illustrated in Figure 2. In the cases of (2) (3), the evolution rule at a boundary point(x = 0 or x = N − 1) in odd time is only to multiply the phase rotation factor as shown below. (We show only the case x = 0 as the case x = N − 1 is essentially the same).
For zero derivative boundary condition [(2)], phase rotation factor is 1 as
Figure 2. Illustration of 3 boundary conditions. (1) Periodic boundary condition, (2) Zero derivative (or symmetric) boundary condition, (3) Zero amplitude (or anti-symmetric) boundary condition. Points from x = 0 to N − 1 constitute the principal region and both sides of it are subsidiary regions.

For zero amplitude boundary condition [(3)], phase rotation factor is 

Note that the unitarity is always satisfied, because the probability increase and decrease are balanced between left and right boundary grid points in the case of (1) and they are zero in the case of (2) (3).
Boundary conditions and discontinuities (inhomogeneities) for QCA are firstly investigated by Meyer. He investigated more general 2-component QCA having two angle parameters. The scalar QCA we use is the simplest one having only one angle parameter, which corresponds to one of factors if his QCA is flattened (namely changed from 2-component to scalar by doubling the number of grid points) and is factorized [23] (2-step QCA of Section 6).
2.3. Multidimensional QCA
It is straightforward to construct multi-dimensional QCA. We have only to use direct product of 2 ´ 2 local unitary 1D matrices to generate 2D matrices.

The rule is illustrated in Figure 3. Concretely

(where x, y are even if t is even, and x, y are odd if t is odd.)
As we know each U approximately corresponds to the evolution
Figure 3. Two-dimensional QCA. At an even time, 4 amplitudes of red quadrilateral are updated by the corresponding local unitary matrix
or 

other, 

generate multidimensional QCA for general dimension.
Applications of QCA to multidimensional cases are studied in [7] [8] [9] . In multidimensional QW, less straightforward (namely not direct product) models are mainly studied, where the number of internal states is not 
2.4. Multiparticle QCA
It is also straightforward to construct (non-interacting) multiparticle QCA. D- dimensional distinguishable M-particle system is equivalent to DM-dimensional 1-particle system. For indistinguishable particle systems, we have to restrict this space to symmetric or anti-symmetric subspace according to the statistics of the particles. Note that 

3. Second Quantized Form of QCA
3.1. Concrete Evolution Rule of 2nd Quantized QCA
If the one-particle time evolution rule is given by an infinitesimal time evolution matrix, namely, a generator or a Hamiltonian, it is straightforward to construct a 2nd quantized Hamiltonian 

(Here 

If the one-particle time evolution rule is given not by a generator but by a finite time evolution matrix 


Namely we can apply the substitution rule

We now apply this substitution rule to 1D free bosonic QCA system where unitary transformation only between nearest neighbor grids occurs, and the one step evolution is given by

The explicit local unitary evolution matrix for the grid pair 

(local unitary matrices for other grid pairs 
We then apply the substitution rule to 1D free fermionic QCA system. Focusing on the grid pair

Here 



It should be noted that if periodic boundary condition is adopted for the grid pair



3.2. MPS Approximation of QCA
Now we introduce an interaction between particles. For this purpose, it is reasonable to introduce an additional phase rotation factor by the potential caused by other particles just like the external potential case.
Note that QCA with external potential was firstly studied by Meyer [4] . QCA with the nearest neighbor pair interaction was studied also by Meyer [3] and Boghosian [8] and Schumacher and Werner [9] in the form we present here.
Here we discuss the simplest case, namely the cases where the nearest neighbor interaction is included. We assume that interaction occurs as an additional phase rotation only when two particles exist in the neighboring grids. In the context of QLGA (two-component QCA), this additional phase rotation corresponds to the phase shift by the collision between the left-going and the right going particles [3] . Under this assumption, the 4 ´ 4 local unitary evolution matrix becomes

Here 

Note that in this simplest case, the structure of evolution scheme is kept same as the structure of free fermion case. After preparing this form, we can apply a MPS approximation and a usual TEBD algorism illustrated by Figure 4 and Figure 5. A general wave function for the 2nd quantized form of QCA is approximated by MPS as

(for the 8 grid points case, m is the dimension of auxiliary spaces and the shape of tensor 


Here SVD is applied then the subspace corresponding to small singular values is truncated in order to keep the dimension of auxiliary space to the given value (m in this case).
Figure 4. MPS approximation of wave function of 2nd quantized QCA and its time evolution. This is an example of 8-grid system. A general wave function of the 2nd quantized QCA is represented by a rank-8 tensor. Firstly this rank-8 tensor is approximated by the MPS form (namely by the contraction of 8 low rank (rank-3 or rank-2) tensors). Then the 2nd quantized QCA rule is applied upon the time evolution, namely the contraction with the tensors, four Us (even time) or three Us plus two 

Figure 5. Time evolution in the TEBD algorithm. When the tensor U is applied to the MPS wave function, the original MPS form is destroyed (Left). In order to recover the original MPS form, firstly SVD is applied (Right), then truncate the small singular values which constitutes the part of the contraction “d” so that the dimension of “d” is equal to the dimension of “d”.
For zero derivative or zero amplitude boundary condition, at an odd time, the end points are updated by applying the 2 ´ 2 diagonal unitary matrix

Finally in this section, we compare our method with the ordinal way of reaching the TEBD algorithm. Basically so called hopping term representing kinetic energy part in evenly-spaced-grid-base (or site-base) quantum models such as Hubbard model or fermionized XXZ model is derived from the FDM-ap- proximation of kinetic energy term. The FDM-approximated Hamiltonian matrix of one-particle TDSE is given by

(Here 
And, its 2nd quantized Hamiltonian for non-interacting fermions is

(The 1st term is so called hopping term. 
By adding neighboring interaction term and dropping external potential term and constant term for simplicity, we have fermionized XXZ model [27] [28] , where only nearest neighbor grid point of occupation number 


If the anisotropy parameter
The XXZ spin model and its equivalent fermionized version are well studied [27] . The phase diagram of the XXZ spin model in extended systems with the external magnetic field consists of 3 phases, ferromagnetic, paramagnetic and antiferromagnetic phases. When the magnetic field is zero, 
According to the TEBD algorism, we decompose the Hamiltonian into two parts.

Time evolution during the small time 

As terms 



(This is QCA-like evolution). As each factor is finite matrix, we can obtain easily its matrix representation using the standard matrix representation of creation and annihilation operator as follows.


We see the exact correspondence of the hopping term parameter in the model Hamiltonian 




4. Boson Approximation by Fermionic QCA
4.1. Formalism
As shown in Equation (18) and Equation (20), the grid pair evolution matrix for bosonic QCA is infinite size matrix, whereas that of fermionic QCA is reduced to 4 ´ 4. It is desirable if bosonic QCA is well approximated by a QCA with small degree of freedom as in the fermionic QCA.
We propose here boson approximation by fermionic QCA (or QCA with a hard core condition) when occupation number per grid is small. We mean by the hard core condition that at most one-particle can reside in one grid point. (We not necessarily mean



In order to make it easy to understand, we compare with the free fermion case, where no interpolation is needed, namely we set the amplitudes where 

Figure 6. Fermion or “Boson approximation” in two-particle QCA. We assume that 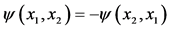


symmetric with respect to exchange of

(where we set
For 2-particle Boson approximation case, 



Under this assumption, we have the following evolution rule.

This implies, the 4 by 4 Unitary matrix in 2nd quantization formalism changed from that of Fermion case as follows

As mentioned before, this 4 ´ 4 unitary matrix is the same as that of the fermion system (fermionized XXZ) with nearest neighbor attractive interaction 
We give another possible interpretation of Equation (34). The boson approximation Equation (34) can be obtained by applying coarse graining to Equation (18) using the following seemingly reasonable weight matrix for the adjacent grid pair subspace. Namely the 11 - 11 component of Equation (34) (=1) is obtained also by

Here, coarse graining means that three states of the adjacent grid pair, namely

4.2. Sample Simulation
Here we show examples of the QCA-TEBD application with the boson approximation. In our simulations, we adopt the minimal auxiliary space dimension for MPS which can describe any 1-slater wavefunction (namely 






We can verify that

For example, in 2-particle case, using the standard representation of Fermion creation and annihilation operators
we have

We simulated 2-particles in a one-dimensional box using imaginary time evolution.
At t = 0 we set 2-particles at adjacent two grid points near the center position.
In Figure 7 we show converged density distributions for N = 64,256 and 


For 

Similarly we computed MPS wave function for the three particle system and the results are shown in Figure 8.
In general the parameter of the interaction must be scaled properly when the grid spacing is changed in order to obtain the same continuum limit waveform. It is reasonable that when 


In Figure 9 we show the ratio of sum of the truncated norms of singular values to that of all singular values for N = 64,256 and 
Figure 7. Converged density distribution of two-particle system (
are sufficiently small and MPS approximation must be good for the case. Theoretically the ratio should be zero for the free fermion case
In Figure 10, we show the converged density distribution 





where
Finally we provide here more detailed information about simulation methods
Figure 8. Converged density distribution of three-particle system (
we adopted, though this is not the main purpose of this study. To perform imaginary time simulation, we set simply 
5. Simulation by 1st Quantized Form of QCA
In this section we explain how to perform the equivalent simulation by the 1st
Figure 9. The ratio of sum of the truncated norms of singular values to that of all singular values in the two-particle system. Upper: N = 64 (t = 0 to 10,000), Lower: N = 256 (t = 0 to 20,000).
quantized form of QCA. Of course in contrast to the above QCA-TEBD simulation, this can be performed only when the number of grids or particles is small (notorious exponential wall for large number problems) . But as it is simple and free from the particle number conservation problem, the result can be used as a reference to the QCA-TEBD simulation. Moreover there are no fundamental difficulties, in simulating bosonic or higher dimensional systems by the 1st quantized form. We already explained the relation between the 1st quantized QCA and the 2nd quantized QCA in the free particles case, we here explain how to treat the additional phase rotation caused by interactions in the 1st quantized QCA. Firstly we explain the 1D-2 particle case. One step evolution is given by Equation (43).
Figure 10. Converged density distribution 





At an even or odd time the evolution rule Equation (43) is applied to each even or odd quadrilateral (namely red or blue quadrilateral in Figure 6) respectively. Precisely the rule Equation (43) is for the bulk. At the zero boundaries the application of U in 
The algorithm of the 1st quantized form of QCA is basically independent of particle statistics. The only procedural difference between boson and fermion is in symmetrization or anti-symmetrization at each simulation step. Without this anti-symmetrization however a decay from a fermionic state to a bosonic state occurs occasionally.
In more general 1D M-particle case, 





In higher dimensional case, the free evolution part 
In a case of higher dimension or many particles, the requirement for the magnitude of 
one simulation step to


space and 

the memory only for the simplex region 
In the following, we show two imaginary time 1st quantized QCA simulations, one is 1D 4 particle fermionic and corresponding bosonic system, the other is 2D 2 particle fermionic and bosonic systems.
The Hamiltonians related to the fermionic and bosonic QCAs we simulate are


where 

We show the result of 1D 4 particle and 2D 2particle imaginary time simulations in Figure 11 and Figure 12 respectively. We already showed in QCA-TEBD simulation that the fermionic 1D system with 

Figure 11. Converged density distribution of the 1D 4 particle fermionic and bosonic imaginary time simulations. 


Figure 12. Converged 1-particle reduced density distribution in the 2D 2-particle 1st quantized QCA simulations. 






the 1D fermionic system with 


By seeing Figure 12 one might expect that fermionic 2D system with 

In Figure 13 we show the applicable parameter range of boson approximation in 2/3/4 particle systems. For 1-body-reduced density distribution for bosonic system are well approximated by that of fermionic system when



6. Multi-Step QCA and Dirac Cellular Automaton
In this supplementary section, we briefly discuss the possibility of multi-step QCA. Firstly we discuss QW and Dirac Cellular Automaton (DCA) [25] [33] [34] as special cases of multi-step QCA. The 1D simplest (namely having only one 2 × 2 unitary matrix as parameters) QW/DCA are mathematically equivalent
Figure 13. Illustration of the applicable range of boson approximation in the 1D 2/3/4-particle case (N = 64, 



to the corresponding QCA. This equivalence is easily shown by using the factorization form of the two-grid translationally invariant banded unitary matrix (namely multi-step QCA form) [9] [23] . In order to interpret QW/DCA as QCA, they are flattened to scalar models as shown in Figure 14.
Namely their two components (up and down) are assigned to two amplitudes of adjacent grid points in the lattice of which the number of grid points are doubled from the original lattice. The 2 ´ 2-unit Z-transformation representation [23] of QCA, QW and DCA are given as



respectively. Here 

shift in the flattened lattice and 
mation representation of the one-grid shift matrix defined by Equation (6). Note that

Now we rewrite 

Figure 14. QCA interpretation of QW or DCA. QW or DCA can be interpreted as two-step (




Considering 


where
(51) are added in order to clarify the correspondence between the expressions and the graphs in Figure 14.
By taking the logarithm of 

The corresponding Hamiltonian is


where

The case 




In order to be able to connect this QCA with the Dirac equation, in the wave number 





the DCA case 

DCA more suitable in connecting to Dirac equation.
As we explained above (Equations (50) (51) and Figure 14), the TDSE/Di- rac-type QW/DCA can be regarded as special case of two-step QCA and moreover mathematically equivalent to two sets of TDSE-type single-step QCAs. Therefore the same arguments about the boundary condition, the 2nd quantiza- tion formalism, the simplest interaction and the boson-fermion corresponding as in QCA apparently hold. Moreover in TDSE/Dirac type multi-step QCA the similar argument would be possible, though we need more investigation about what essentially new phenomenon could appear by extending the single-step QCA to the general multi-step QCA (Equation (49)).
7. Conclusion
In this study we show that in one-dimensional multiparticle QCA, the approximation of the bosonic system by fermion (boson-fermion correspondence) can be derived in rather a simple and intriguing way, where the principle to impose zero-derivative boundary conditions of one-particle QCA is also analogously used in particle-exchange boundary conditions. As a clear cut demonstration of this boson approximation, we calculate the ground state of 2 or 3-particle systems in a box using imaginary time QCA-TEBD simulation. Obtained ground states are indeed boson-like. We also perform imaginary time simulations by the 1st quantized form of QCA not only for fermionic system but also for bosonic system and show the applicable range of boson approximation (boson-fermion correspondence
Acknowledgements
This work was supported by Education Center for Next-generation Simulation Engineering, Toyohashi University of Technology and University-Community Partnership Promotion Center, Toyohashi University of Technology. We would like to thank Prof. Hitoshi Goto for his support and Dr. Akira Saitoh for his helpful advice.
Cite this paper
Hamada, S. and Sekino, H. (2017) The Approximation of Bosonic System by Fermion in Quantum Cellular Automaton. Journal of Quantum Information Science, 7, 6-34. https://doi.org/10.4236/jqis.2017.71002
References
- 1. Wiesner, K. (2009) Quantum Cellular Automata. In: Meyers, R.A., Ed., Encyclopedia of Complexity and Systems Science, Springer, New York, 7154-7164.
https://doi.org/10.1007/978-0-387-30440-3_426 - 2. GrÖssing, G. and Zeilinger, A. (1988) Quantum Cellular Automata. Complex Systems, 2, 197-208.
- 3. Meyer, D.A. (1996) From Quantum Cellular Automata to Quantum Lattice Gases. Journal of Statistical Physics, 85, 551-574.
https://doi.org/10.1007/BF02199356 - 4. Meyer, D.A. (1997) Quantum Mechanics of Lattice Gas Automation: One-Particle Plane Waves and Potential. Physical Review E, 55, 5261-5269.
- 5. Meyer, D.A. (1998) Quantum Mechanics of Lattice Gas Automata: Boundary Conditions and Other in Homogeneities. Journal of Physics A, 31, 2321-2340.
https://doi.org/10.1088/0305-4470/31/10/009 - 6. Meyer, D.A. (1997) Quantum Lattice Gasses and Their Invariants. International Journal of Modern Physics C, 8, 717-735.
https://doi.org/10.1142/S0129183197000618 - 7. Boghosian, B.M. and Taylor IV, W. (1998) Quantum Lattice-Gas Model for the Many-Particle SchrÖdinger Equation in D Dimensions. Physica Review E, 57, 54-66.
https://doi.org/10.1103/PhysRevE.57.54 - 8. Boghosian, B.M. and Taylor IV, W. (1998) Simulating Quantum Mechanics on a Quantum Computer. Physica D, 120, 30-42.
https://doi.org/10.1016/S0167-2789(98)00042-6 - 9. Schumacher, B. and Werner, R. (2004) Reversible Quantum Cellular Automata.
- 10. Arrighi, P., Nesme, V. and Werner, R. (2011) Unitarity plus Causality Implies Localizability. Journal of Computer and Systems Science, 77, 372-378.
https://doi.org/10.1016/j.jcss.2010.05.004 - 11. Arrighi, P. and Grattage, J. (2012) Partitioned Quantum Cellular Qutomata Are Intrinsically Universal. Journal of Natural Computing, 11, 13-22.
https://doi.org/10.1007/s11047-011-9277-6 - 12. Venegas-Andraca, S.E. (2012) Quantum Walks: A Comprehensive Review. Quantum Information Processing, 11, 1015-1106.
https://doi.org/10.1007/s11128-012-0432-5 - 13. Succi, S. and Benzi, R. (1993) Lattice Boltzmann Equation for Quantum Mechanics. Physica D: Nonlinear Phenomena, 69, 327-332.
https://doi.org/10.1016/0167-2789(93)90096-J - 14. Succi, S., Fillion-Gourdeau, F. and Palpacelli, S. (2015) Quantum Lattice Boltzmann Is a Quantum Walk. EPJ Quantum Technology, 2, 12.
https://doi.org/10.1140/epjqt/s40507-015-0025-1 - 15. Hamada, M., Konno, M. and Segawa, E. (2005) Relation between Coined Quantum Walks and Quantum Cellular Automata. RIMS Kokyuroku, 1422, 1-11.
- 16. Shakeel, A. and Love, P.J. (2013) When Is a Quantum Cellular Automaton (QCA) a Quantum Lattice Gas Automaton (QLGA)? Journal of Mathematical Physics, 54, Article ID: 092203.
- 17. Hooft, G. (2014) The Cellular Automaton Interpretation of Quantum Mechanics. A View on the Quantum Nature of Our Universe, Compulsory or Impossible?
https://arxiv.org/abs/1405.1548 - 18. Zhang, W.-R. (2016) G-CPT Symmetry of Quantum Emergence and Submergence—An Information Conservational Multiagent Cellular Automata Unification of CPT Symmetry and CP Violation for Equilibrium-Based Many-World Causal Analysis of Quantum Coherence and Decoherence. Journal of Quantum Information Science, 6, 62-97.
https://doi.org/10.4236/jqis.2016.62008 - 19. Hamada, S. and Sekino, H. (2016) Solution of Nonlinear Advection-Diffusion Equations via Linear Fractional Map Type Nonlinear QCA. Journal of Quantum Information Science, 6, 263-295.
https://doi.org/10.4236/jqis.2016.64017 - 20. Vidal, G. (2003) Efficient Classical Simulation of Slightly Entangled Quantum Computations. Physical Review Letters, 91, Article ID: 147902.
https://doi.org/10.1103/physrevlett.91.147902 - 21. Vidal, G. (2004) Efficient Simulation of One-Dimensional Quantum Many-Body Systems. Physical Review Letters, 93, Article ID: 040502.
https://doi.org/10.1103/physrevlett.93.040502 - 22. White, S.R. (1993) Density-Matrix Algorithms for Quantum Renormalization Groups. Physical Review B, 48, Article ID: 10345.
https://doi.org/10.1103/PhysRevB.48.10345 - 23. Hamada, S., Kawahata, M. and Sekino, H. (2013) Solution of the Time Dependent Schrodinger Equation and the Advection Equation via Quantum Walk with Variable Parameters. Journal of Quantum Information Science, 3, 107-119.
https://doi.org/10.4236/jqis.2013.33015 - 24. Chandrashekar, C.M. (2013) Two-Component Dirac-like Hamiltonian for Generating Quantum Walk on One-, Two-and Three-Dimensional Lattices. Scientific Reports, 3, 2829.
https://doi.org/10.1038/srep02829 - 25. D’Ariano, G.M. and Perinotti, P. (2014) Derivation of the Dirac Equation from Principles of Information Processing. Physical Review A, 90, Article ID: 062106.
https://doi.org/10.1103/physreva.90.062106 - 26. Arrighi, P, Nesme, V. and Forets, M. (2014) The Dirac Equation As a Quantum Walk: Higher Dimensions, Bb Servational Convergence. Journal of Physics A: Mathematical and Theoretical, 47, Article ID: 465302.
https://doi.org/10.1088/1751-8113/47/46/465302 - 27. Samaj, L. (2010) Introduction to Integrable Many-Body System II. Acta Physica Slovaca, 60,155-257.
https://doi.org/10.2478/v10155-010-0002-2 - 28. Jordan, P. and Wigner, E. (1928) über das Paulische Äquivalenzverbot. Zeitschriftfür Physik, 47, 631.
- 29. Tomonaga, S. (1950) Remarks on Bloch’s Method of Sound Waves Applied to Many-Fermion Problems. Progress of Theoretical Physics, 5, 544.
https://doi.org/10.1143/ptp/5.4.544 - 30. Luttinger, J.M. (1963) An Exactly Solvable Model of a Many-Fermion System. Journal of Mathematical Physics, 4, 1154.
https://doi.org/10.1063/1.1704046 - 31. Girardeau, M. (1960) Relationship between Systems of Impenetrable Bosons and Fermions in One Dimension. Journal of Mathematical Physics, 1, 516.
https://doi.org/10.1063/1.1703687 - 32. Cazalilla, M.A., Citro, R., Giamarchi, T., Orgnac, E. and Rigol, R. (2011) One Dimensional Bosons: From Condensed Matter Systems to Ultracold Gases. Review of Modern Physics, 83, 1405.
https://doi.org/10.1103/RevModPhys.83.1405 - 33. Bisio, A., D’Ariano, G.M. and Tosini, A. (2015) Quantum Field As a Quantum Cellular Automaton: The Dirac Free Evolution in One Dimension. Annals of Physics, 354, 244-264.
https://doi.org/10.1016/j.aop.2014.12.016 - 34. Mallick, A.M. and Chandrasekar, C.M. (2016) Dirac Cellular Automaton from Split-Step Quantum Walk. Scientific Reports, 6, Article No. 25779.
https://doi.org/10.1038/srep25779






















