Received 10 June 2015; accepted 13 September 2015; published 16 September 2015

ABSTRACT

We calculate the work done by a Landau-Zener-like dynamical field on two- and three-level quantum system by constructing a quantum power operator. We elaborate a general theory applicable to a wide range of closed-quantum system. We consider the dynamics of the system in the time domain (where is the LZ transition time in the sudden limit) where the external pulse changes its sign and its action becomes relevant. The statistical work is evaluated in a period 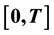where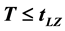. Our results are observed to be in good qualitative agreement with known results.

Keywords:

Power Operator, Statistical Work, Landau-Zener Model, Level Crossing

1. Introduction

The pioneering work of Jarzynski establishes a non-trivial relation between the non-equilibrium work performed on a thermally insulated classical system and the change in its equilibrium free energy [1] . This expression became a coner stone of theories discussing non-equilibrium statistical mechanics and reads

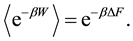(1)

Here, 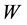is the work, 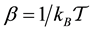where 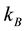and 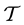are respectively the Boltzman constant and absolute temperature. The brackets denote the ensemble average over all possible realizations of the work

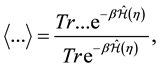(2)

where is the total Hamiltonian and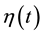, the control protocol. 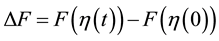is the free energy difference between a reference equilibrium state of the system and a state achieved at time t by changing the protocol 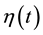during the work. The Jarzynski equality holds irrespectively of whether the system ever reaches this reference equilibrium state. Even out of equilibrium, it proved to be applicable. The Jarzynski equa- lity has been extended to quantum regimes and experimentally tested [2] - [4] . It was accurately studied in single- electron transport [5] - [7] and molecular systems [8] . It was applied in Refs. [9] and [10] to produce the cooling of nanomechanical resonators and atoms.

Though Equation (1) is extended to quantum systems, a key and natural question arised: does it still hold in a more realistic situation where the system remains in thermal contact with its environment while the forcing protocol is in action? An affirmative answer to this question was given by Crooks based on classical arguments [11] [12] . He proved this by showing that the Jarzyinski equality can be derived from a fluctuation theorem [11] [12] .

The experimental measurements of the proper free energy of a system lead to the average exponentiated work using Equation (1). This measurement is not always easily performed experimentally. The determination of the proper work has turned out to be a non-trivial task [13] - [15] . It attracted a lot of remarkable attentions and fed several scientist debates [13] - [18] . In order to find the work done by changing an external protocol on a quantum system, it is recommended to find the work operator [16] - [18] . Though this reasoning is quantum mechanically founded, it has quickly presented serious drawbacks [16] . The work does not depend on the instantaneous eigenstates of the system. It essentially depends on the process involved [17] [18] . Therefore, for open systems, the work cannot be defined by a local time-dependent operator. This is not an issue for closed systems [17] [18] .

The present paper is devoted to the calculation of the work done by an external field of constant amplitude on two- and three-level isolated systems. The systems are assumed to be thermally isolated from their environ- ments. We consider as in Ref. [19] that the work can be experimentally measured by the two-measurement process (TMP) [20] - [22] . The work corresponds to the change of the internal energy of the system. The TMP suggests a measurement of the internal energy between the initial and the final times 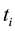and. The relevant work corresponds to the difference between the associated internal energies. The work is statistically distributed. The experiment should be repeated under the same experimental protocol. In order to ensure a thermal equili- brium between two measurements, we demand a long enough time between two experiments. Assume that the system behavior is appreciable between the times t_i and t_f. Consider the difference Hamiltonian operator that the average yields the change on the internal energy. Basically, this lies on the variation of the functional of the protocol. We define the power injected during this evolution as where is the time necessary to produce a transfer of population. If one defines the power operator:

(3)

Here, the overdot denotes the time derivative. The average statistical work done during a period T on any quantum system is statistically defined as:

(4)

This formula is employed throughout this paper.

The paper is organized as follows: In Section 2, we present a general theory for calculating the work done on a coherently driven system. In Section 3, the theory is applied and tested on two-level system subjected to inter- band LZ transitions [23] -[26] . The same philosophy/strategy is extended to a three-level system yet subjected to LZ tunneling effects in Section 4.

2. Work and Fluctuations on Multi-Level Systems

The procedure for calculating the work done during transitions between Zeeman multiplet is illustrated. We consider systems on which act simultaneously a strong time-dependent diagonal field and a slowly varying perpendicular field. The prototype Hamiltonian describing these effects are written in the diabatic basis (basis of the eigen-states of the Hamiltonian in the absence of couplings) as follows:

(5)

The dynamical symmetry associated with (5) is referred to as and is isomorphic to the relevant su(2) algebra. The model effectively describes the evolution of a system driven by a time-

dependent control protocol. The coupling between the two groups of diabatic

states and is assumed real and constant.

The protocols and are approximately linear functions of time. The corresponding diabatic trajectories cross j-times creating thus j-level-crossing (see Figure 1). The system evolves on a LZ grid and the population transfer is made through several resonant points. The statistical work is essentially due to the tunneling Landau-Zener process [23] -[26] .

During the work, the system passes through a sequence of several configurations (non necessarily equili- brated). If the states of the system are described by the reduced density matrix operator:

(6)

then, the statistical average of an arbitrary time-independent operator is given by

(disordered average). For our case, the eigen-spectrum is discrete and characterized by the components of

the total wave-function where is the system time-evolution operator (

where is the unit operator constructed by considering irreducible representation of). Consequently, it is convenient to work in the Heisenberg picture. Thus,

(7)

where H indicates the Heisenberg picture. The thermal and statistical averages are taken as:

(8)

Our goal is thus achieved once the evolution operator is constructed. This construction is process- dependent.

The first and the second moments of the work whatever the process involved are respectively given in the Heisenberg picture by:

(9)

and

(10)

Here, the power operator is basically a function of the fermionic occupation number defined

such that. The states of the group and form an orthogonal basis,.

As an important remark, evaluation of and requires the fermionic average occupation number:

(11)

and

(12)

where we have defined the transition amplitudes

(13)

and

(14)

The transition amplitude refers to the probability amplitude of transition from the diabatic state to at a given moment. The two-time transition amplitude describes an occupation of the diabatic state when the system has consecutively passed and.

The measurement of the instantaneous eigen-energies (measured observable) associated with the eigenfunctions are needed. This permits to evaluate the work values done on a -level system. Both obey the Sturm-Liouville equation:

(15)

Once the eigenvalues are obtained, the transfer matrices for the intermediates trajectories are deduced:

(16)

where

(17)

Between measurements, the system propagator describing a set of transitions through the j-crossing points is expressed as follows:

(18)

Consider the states of a system with a total spin S with symmetry operations that belong to the group. The components of the transition matrix can be constructed in the basis of Jacobi polynomials [27] - [29] :

(19)

Here, are Jacobi polynomials. Stockes phases should be introduced. The diagonal elements are written by noting that when the probability for making a transition is, then the probability for not making a

transition is. Hence the off-diagonal amplitudes are multiplied by a phase factor where

is the Stockes phase at time:

(20)

Here, is the gamma function, is the Landau-Zener parameter defined at the anti-crossing point where the transition from the diabatic state to is executed. Here, the dot on functions denotes time derivative and are constant sweep velocities of transverse fields.

A point of concern for introducing is that should be unitary. Based on the above defini- tions, the full propagator can be calculated. This permits to find the transitions amplitudes and from Equations (13)-(14). This can be done by connecting adiabatic and the diabatic states of the system through the relation:

(21)

with being the matrix elements of a rotation matrix which ensures connection between the two diffe- rent bases of a system with a total spin S.

The average occupation number are deduced, leading thus to an average power operator. A first consequence being the possibility to evaluate the average work. The second moments of the work needs which also demands to have.

3. Quantum Work and Fluctuations on Two-Level System

We illustrate the theory presented above by considering the simplest case of the spin-1/2 two-level system.

3.1. The Model Hamiltonian

The model Hamiltonian considered is deduced from Equation (5) as,

(22)

The two instantaneous eigenvalues and eigenfunctions relevant to (22) should be evaluated. The results read:

(23)

where

(24)

is the level-separation energy and a detuning. The eigenfunctions associated with the eigen-energies Equation (23) are respectively given by:

(25)

(26)

where the normalization factors and are given by:

(27)

For spin-1/2 considered, adiabatic and diabatic states in Equations (25) and (26) are related as suggested in Equation (21) by the rotation matrix:

(28)

with with. This matrix helps to rotate a system from its adiabatic to diabatic basis and vis versa. A Caley-Klein algebra can be attributed to (28).

The projections of the instantaneous eigenfunctions in the diabatic basis are needed:

(29)

Here, , , and. In the above repre-

sentation,. Similarly, map.

Our analyzes of the work done on a two-level system are mainly performed in the limits and. These limits can be respectively interpreted as sudden and adiabatic limits of transitions. In the slow drive regime, the process is quasi-static and the system passes through a sequence of equilibrium states and remains in its original adiabatic state according to the adiabatic theorem for a sufficiently slow vari- ation [28] . In the rapid drive regime, the two-level system will not feel the gap. For each of these extremal regimes, a projection matrix is constructed,

(30)

which is achieved in the sudden limit while

(31)

is the one obtained for the counterpart. It is instructive to note that the matrix of projections onto the eigenspace satisfy:, where is the unit matrix. This last remark implies a conservation of the total population in the sudden and adiabatic limit.

These data are helpful to evaluate the work done on a two-level system by an external field of constant amplitude.

3.2. Work and Fluctuations by the LZ Effect

The LZ process describes the dynamics of two states which come close by linear variation of a control protocol:

(32)

The energies defined such that are diabatic energies associated with diabatic states and (see Figure 2(b)) and cross at time while adiabatic energies are plotted on the Figure 2(a). They do not cross but hybridize at and form an avoided level crossing. Super-conducting Cooper-pair box (CPB) is one of the experimental setups in which LZ transitions are observed.

The time-evolution of the transition probability function during the rapid and slow drives show that nothing happens to the system before the crossing. It mainly remains in its initial state exhibiting an insensitivity to the external sweeping protocols. The work is converted to heat and accumulated in the region. After passing the avoided crossing, the heat is consumed to produce LZ-like transitions. We take the initial time and the final time i.e we consider the system in the region where the effects of the control protocol is effective.

Considering the Hamiltonian (22), the power operator for a two-level system is explicitly evaluated as:

(33)

where. We used the relation.

The average work done during a period T to transfer a population from the state to will be

derived using the formula:

(34)

where is the average population transferred. The second-order moment of the work in (43) is calculated as well:

(35)

Here,

(36)

The average of the square fluctuations of the work, is evaluated from:

(37)

The full propagator for the two-level system driven by the traditional LZ process (single crossing time) is expressed as:

(38)

Here,

(39)

with

(40)

being the phase accumulated by the components of the wave-function from to t and. The eigen- energies and are symmetric about the resonance (see Figure 2). The phases in (40) are also symmetric. The transition matrix reads:

(41)

where the angle defined by:

(42)

is the Stockes phase. The function is the LZ probability for occupying the same diabatic state after passing the anti-crossing region. Here, is the relevant LZ parameter.

In the sudden limit of transition, , the system is in one of its diabatic states or. In this regime, the ground state at time can either be or. The two components of the wave function are:

(43)

(44)

Substituting the instantaneous eigenstates (25) and (26) into the above expressions yields the transition amplitudes. Another way to find the transition amplitudes is to consider the projections of the states (43) and (44) onto the diabatic basis (,). This will involve the projections in Equation (28). The average population

transferred from to are obtained as follows:

(45)

(46)

(47)

and

(48)

In these relations, projections of instantaneous eigenstates read:

In the regime the instantaneous projections are given by Equation (29). The average population for the transition and leads to the same result, namely:

(49)

Thus, the statistical average works done on the two-state system are given by:

(50)

and

(51)

In principle, for the Landau-Zener drive,. In absolute values, the two works in Equations (50) and (51) are identical.

An algebraic character can be associated with the quantum work. The work is antisymmetric by path reversal. By changing the protocol, this affects the work by inverting its sign:

(52)

In addition, it should also be noted that

(53)

Because of the link between work and heat, the properties in Equations (52) and (53) can be attributed to the heat.

Recall that is the work done on a two-level system to realize a transfer of population from the diabatic state to. This work is positive; we call it “foward work”. On the other hand, the work which corresponds to the opposite trajectory is negative; we call it “backward work”.

A particular characteristic for a quantum work similar to that of classical work should be pointed out. Basi- cally, the work done on a classical system does not depend on the followed path but only on the initial and final positions. Relations (50) and (51) show a contrasted situation in the regime of sudden transitions. Namely, the work done on a quantum two-level system does not depend on the followed path. It does not depend yet on the initial and the final states. The initial state can be chosen arbitrary, the efficiency remaining the same.

In the regime the instantaneous projections are given by Equation (30). Populations transferred are deduced from Equation (45)-(48) as follows:

(54)

(55)

The occupation probability,. The maximum occupation of diabatic states is 1/2. The ”forward work”

or the “backward work” performed are not statistically enough to produce a com-

plete transfer. Both diabatic states remain constantly coupled and the total population is preserved,

.

An alternative way to find the work done on a system is defined through the two-measurement process (TMP) [20] - [22] . The internal energy acquired during the passage is measured at the begin-

ning and at the end of the evolution. The work done during the process is predetermined by the corresponding energy difference,. We show that this approach is equivalent to the previous measurement

procedure for a rapid LZ drive process(non-adiabatic evolution). The work is then defined as:

(56)

Considering the Hamiltonian, the relevant internal energy acquired at time t during the transfer reads:

(57)

As already shown, the transition amplitudes do not depend on time in the sudden limit. The work is obtained as follows:

(58)

This result exactely coincides with the one derived from Equation (35) under the same assumptions.

From a quantum mechanical view point it is more convenient to find the Hamiltonian difference

and average it. This procedure yields:

(59)

which is nothing but the power operator in Equation (33).

4. Quantum Work and Fluctuations on Three-Level System

4.1. The Model Hamiltonian

Here, an additional level position is present. It might evolve with time or not. States are coupled by this intermediate position via a constant coupling. The model is of the form:

(60)

In this representation, and correspond to the triplet states while is the single singlet state (Figure 3).

The associated eigenvalues are expressed as follows:

(61)

Here,

(62)

with

(63)

where is the Gauss hypergeometric function [30] - [32] . Also,

(64)

(65)

and

(66)

Similarly, we have defined

(67)

The instantaneous eigenfunctions are calculated. The results are written as follows:

(68)

(69)

(70)

where

(71)

(72)

(73)

Here,. The notation in (69) indicates the intermediate level position. The detuning is expressed as follows:

(74)

and is generalized as:

(75)

The normalization factor reads:

(76)

where

(77)

For spin-1, we do into Equations (61)-(77). Adiabatic and diabatic states in Equations (68)-(70) are related by the unitary rotation matrix:

(78)

We obtained this matrix by direct calculations. Indeed, the angle is used and the transformation related to are applied. One can see that possesses the effective features of Caley-Klein algebra associated with spin-1 in the group.The projection of the instantaneous eigenfunctions in

the diabatic basis are of the form (28), namely,. One should understand

. Likewise,. The above

relations serve for derivation of transition amplitudes as we did for the case of two-level.

A projection matrix can be constructed. The extreme limits and are considered. After some algebra, in the sudden limit, one has:

(79)

and

(80)

for adiabatic limit. As for the case of two-level, these two matrices obey. Now we can be finding the works done.

4.2. Work and Fluctuations by the LZ Effect

The definition of the work given in the first section is used. The power operator is expressed here as:

(81)

where, and,. The drifts are linear functions of t such that their first order derivative does not evolve with time.

The average of the work can be evaluated with aid of the formula:

(82)

The average in the Heisenberg pictures are to be evaluated as explained in the preceding section. Our goal will be achieved after evaluating the transition amplitudes (13). We do it as follows. The energy diagram shows one crossing point for this process (spin-1 LZ tunneling effects). The full propagator describing the adiabatic evolution could be presented as in Equation (38) where

(83)

and

(84)

The components of adiabatic wave-functions are derived. The relevant transitions amplitudes are deduced as well. For convenience, the results are written in matrix forms:

These representations help to approximate the work done on a three-level system for the sudden and adiabatic limits of transition. For instance, in the sudden limit, it can be shwon that, populations transfered between the three levels correspond to those for spin-1 LZ problem:

(85)

The works in (82) are decomposed as follows:

(86)

(87)

(88)

and correspond each to a diabatic state. As already explained, represents the population which has

been transferred from the diabatic states. The work is performed to produce a transfer from.

Considering the works done on two-level systems, that for three-level in Equations (86)-(88) are the sum of works between intermediate diabatic positions. These works could be constructed intuitively considering intermediate works separately.

Equations (86)-(88) can be transformed with the aid of the components of the matrix in Equation (85). Thus, one obtains:

(89)

(90)

(91)

We have exploited the fact that.

5. Conclusions

We have presented a theory for evaluating the work done on a multi-level system. Two particular cases (two- and three-level) are considered and permit to illustrate the theory. The obtained results for two-level spin-1/2 system were shown to be simple functions of the Landau-Zener probability function. Thus, the work depends on control protocol which can be experimentally manipulated. We have demonstrated that forward work and backward were absolutely identical and differ algebraically by a sign in the sudden limit. The efficiency of the work done has been observed as being independent on the initial state chosen. It has been pointed out that an adiabatic variation of the protocol cannot lead to a complete population transfer when the system is isolated from its environment. The half of the initial population corresponds to the maximum of the population trans- ferable. Both states remain constantly coupled. If one allows the internal energy of such a system to flow out of it or an external energy source to flow towards the system, it will be entangled and its states will no longer be expressible as linear superposition of the states of the subsystem. An equilibrium would not be achieved. The system will mostly evolve out of equilibrium. The work done will be accompanied by an additional work due to the perturbation:

(92)

Here, is the Lindblad operator accounting for relaxation and dephasing if any. The effective power injected will come from two different sources ( protocol and perturbation). The theory we have presented should be reformulated out of equilibrium. However, the variation of the internal energy remains experimentally measurable. We have shown that the work done corresponds to variation of the internal energy.

For three-level system on the other hand, the work to be done in order to achieve a transfer of population from one of the upper (lower) to another lower (upper) diabatic states appeared as being the sum of intermediate works performed independently.

Acknowledgements

The authors thank M. Tchoffo, A. J. Fotue, Kenfack Sadem and F. Ngoran for careful reading of the manuscript and valuable suggestions.

Cite this paper

IssofaNsangou,Lukong CorneliusFai, (2015) Work Done on a Coherently Driven Quantum System. Journal of Quantum Information Science,05,89-102. doi: 10.4236/jqis.2015.53011

References