Journal of Quantum Information Science
Vol.05 No.01(2015), Article ID:55017,9 pages
10.4236/jqis.2015.51002
Alternative Coins for Quantum Random Walk Search Optimized for a Hypercube
Hristo Tonchev
Department of Physics, Sofia University, Sofia, Bulgaria
Email: h_tonchev@phys.uni-sofia.bg
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 September 2014; accepted 24 March 2015; published 25 March 2015
ABSTRACT
The present paper is focused on non-uniform quantum coins for the quantum random walk search algorithm. This is an alternative to the modification of the shift operator, which divides the search space into two parts. This method changes the quantum coins, while the shift operator remains unchanged and sustains the hypercube topology. The results discussed in this paper are obtained by both theoretical calculations and numerical simulations.
Keywords:
Quantum Information, Quantum Random, Quantum Random Walk Search

1. Introduction
The search algorithms for unstructured databases are widely used in statistical data processing for searching the maximum or minimum element or an element corresponding to specific criteria. Effective search algorithms can provide a solution for one of the Non-Deterministic Polynomial Time Complete (NPTC) problems, from which a solution can be found to any NPTC problem by an algorithm with polynomial complexity. These are the reasons for the great interest in the quantum search algorithms and their experimental implementation.
The first quantum search algorithm for unstructured databases is created by Grover [1] and is based on a quantum Fourier transformation. Quantum search on a two-qubit cavity QED database has been done by Yamaguchi et al. [2] . Quantum search on a three-qubit database with NMR has been done by Vandersypen et al. [3] . Grover’s algorithm cannot be used without knowing the exact number of solutions. To find the exact number of elements and satisfy the search criteria, the quantum counting algorithm should be used.
There are already many classical random walk algorithms that perform much better in their tasks than deterministic algorithms. Two classes of such algorithms are Las Vegas algorithms (which always end with a correct result when used for a finite time) and Monte Carlo algorithms (which depend on random input and might produce an incorrect result). Las Vegas algorithms are widely used in fields like artificial intelligence [4] , biology [5] and others. Monte Carlo algorithms are used in mathematics, condensed matter physics [6] - [8] and others.
Another type of quantum algorithms are the ones based on the quantum random walk; they are analogous to the classical random walk. There are two types of those algorithms: continuous time evolution random walk algorithms (CTRWA) and discrete time random walk algorithms (DTRWA). The CTRWA were first introduced by Farhi and Gutmann [9] . They have showed that CTRWA propagate exponentially faster through graphs [10] and can solve any black box problem like searching exponentially faster than any classical algorithm [11] . Childs has shown that the continuous time quantum random walk search algorithms (CTRWS) can find an element in a graph with dimension over 4D faster than Grover’s search algorithm [12] . DTRWA have been first proposed by Aharonov et al. [13] . Examples for DTRWA algorithms are the quantum random walk algorithms for element distinction [14] and the quantum random walk search algorithms [15] . Discrete time random walk search algorithms (DTRWSA) have been first created by Shenvi et al. [15] and are denoted as SKW. The original SKW search algorithm can find an element with probability less than 1/2. Hein has proposed a faster DTRWSA, but to be effective, the initial state of the algorithm should take into account which elements are to be searched [16] . Potocek et al. have shown that if the searched space is divided into two parts, the probability to find a solution can be increased close to 1, with large enough searched space [17] . They also have demonstrated that the probability of finding a solution can be increased if the shift operator is modified to divide the searched space. Tulsi has shown that DTRWSA is faster than Grover’s search when the searched space is two-dimensional [18] .
Grover’s search, CTRWSA and DTRWSA differ conceptually in terms of working principle. This is the reason for their different advantages and disadvantages. Grover’s search algorithm and DTRWSA can be modified to find a solution with probability close to one. Long has shown that Grover’s search can be modified so that the probability of successfully finding a solution with it to be exactly equal to one [19] , which means that the algorithm evolves from a quantum probabilistic to a quantum deterministic method. Potocek et al. have shown that a probability to find solution close to one can be obtained in DTRWSA by two different methods [17] . Grover’s search algorithm needs only one oracle call for each iteration of the algorithm and less number of qubits (as much as needed to store the searched space); let this number be denoted as n. DTRWSA needs more qubits: O(n), and two oracle calls for each iteration [20] . DTRWSA is much better than Grover’s algorithm, when there is the need to search in a register of two or more dimensions [18] [21] .
The present paper is organized as follows. In Section 2, the discrete quantum random walk is reviewed, and the quantum random walk on a line is shown as an example. In Section 3, the quantum random walk on a hyper- cube and the quantum random walk search on a hypercube are reviewed. In Section 4, a new alternative way is demonstrated for the method shown in [17] for dividing the searched space of the algorithm in two, while sustaining the hypercube topology and effectively dividing the searched space by using coins, which unequally distribute the probability of transition to adjacent nodes. In Section 4.1, Householder reflection is reviewed. In Section 4.2, the general form of specialized coins is shown; whereas their use is discussed in Section 4.3. In Section 4.4, some examples of such coins and quantum circuit for their experimental implementation in quantum random walk search algorithm are shown. The results of numerical simulations with the coins are also given. Section 5 is the conclusion of the article.
2. Classical and Discrete Quantum Random Walk, Quantum Random Walk on Line
The classic random walk on a line starts at an initial state 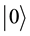 and at every step, a coin is tossed. There is a different probability of the possible outcomes of the toss. The sum of these probabilities is equal to one. Each of the possible outcomes of the toss is associated with a distinct direction, and the directions depend on the structure of the graph which is traveled over. For example, for a line the directions are left and right. For a square grid, the directions are left, right, up and down. The particle moves one step in the corresponding direction, according to the result of the coin toss.
and at every step, a coin is tossed. There is a different probability of the possible outcomes of the toss. The sum of these probabilities is equal to one. Each of the possible outcomes of the toss is associated with a distinct direction, and the directions depend on the structure of the graph which is traveled over. For example, for a line the directions are left and right. For a square grid, the directions are left, right, up and down. The particle moves one step in the corresponding direction, according to the result of the coin toss.
The quantum random walk algorithm is the quantum analogue of the classic random walk algorithm. HC is the Hilbert space of the quantum coin (coin space) and HS is the Hilbert space of the nodes of the structure of the graph. Again, each step of the algorithm (which is described by the operator U) has two parts. First is the coin toss. The coin flip is defined by the unitary operator of the coin C0, which acts in the coin space HC. The coin operator acts upon the Hilbert space  and is denoted by
and is denoted by . The result of the action of the coin operator upon the coin is a chiral state [22] . This is an analogue of the classic probability. As the chiral state is a quantum state, it can be in a quantum superposition of directions. According to the toss outcome, the state of the system is changing. The exact change of the state depends on the structure. The quantum operator which represents this structure is a permutation matrix which performs controlled shift, depending on the state of the coin, and is denoted by S. The operator S acts upon the space
. The result of the action of the coin operator upon the coin is a chiral state [22] . This is an analogue of the classic probability. As the chiral state is a quantum state, it can be in a quantum superposition of directions. According to the toss outcome, the state of the system is changing. The exact change of the state depends on the structure. The quantum operator which represents this structure is a permutation matrix which performs controlled shift, depending on the state of the coin, and is denoted by S. The operator S acts upon the space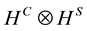 . Summarily, each step of the quantum random walk can be written as:
. Summarily, each step of the quantum random walk can be written as:
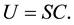 (1)
(1)
An example for a shift operator is SL corresponding to a quantum random walk on a line [23] :
 (2)
(2)
where x is the position of the particle on the line. The values of d (0 or 1) correspond to left and right directions. For the coin, a Hadamard matrix can be used:
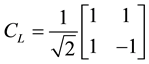 . (3)
. (3)
Summarily, a DQRW step on line can be written as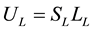 . The classic random walk spreads as a binomial distribution after each step. In DQRW, after each step of the algorithm, quantum interference occurs when more than one possible path exists to reach the respective position. The interference can be constructive or destructive, which leads to very different distribution compared to the classic random walk on a line. The variance in the number of steps t between the classic random walk and DQRW is very different. DQRW spreads as O(t); in comparison, the classic random walk spreads as
. The classic random walk spreads as a binomial distribution after each step. In DQRW, after each step of the algorithm, quantum interference occurs when more than one possible path exists to reach the respective position. The interference can be constructive or destructive, which leads to very different distribution compared to the classic random walk on a line. The variance in the number of steps t between the classic random walk and DQRW is very different. DQRW spreads as O(t); in comparison, the classic random walk spreads as  [23] . If the quantum random walk is measured at each coin flip, or after the end of each step, it will revert to the classic random walk [15] .
[23] . If the quantum random walk is measured at each coin flip, or after the end of each step, it will revert to the classic random walk [15] .
3. Quantum Random Walk and Search on a Hypercube
The hypercube is a graph with 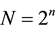 nodes and n edges between nodes. Each one of the nodes will be denoted by a n-bit string
nodes and n edges between nodes. Each one of the nodes will be denoted by a n-bit string . Two nodes of a hypercube,
. Two nodes of a hypercube,  and
and  are connected only if the modulus of hamming weight of their difference is equal to one:
are connected only if the modulus of hamming weight of their difference is equal to one: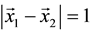 . That is why the Hilbert space of the coin is
. That is why the Hilbert space of the coin is , the Hilbert space of the nodes is
, the Hilbert space of the nodes is 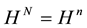 and the Hilbert space of the random walk is
and the Hilbert space of the random walk is 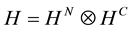

where d is the direction of the motion and 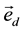
The Grover coin G is frequently chosen for a coin for quantum random walks on a hypercube. This coin is invariant to all permutations of the n edge directions, so it sustains the permutation symmetries of the hypercube.

where I is identity operator, 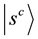
To make a quantum random walk search algorithm, a quantum oracle should be applied that marks the wanted element by applying a coin upon it. The oracle does this by using the function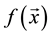
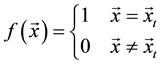
Summarily, the operator of the coin becomes:
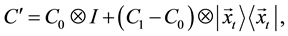
where C1 can be almost any unitary operator but most often it is taken
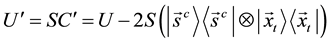
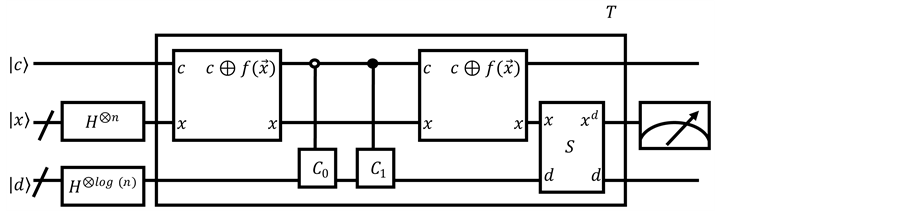
The quantum circuit of the random walk search algorithm is shown in Figure 1 [15] . This circuit does not actually depend on the shape of the searched graph. When the graph is different, the shift operator S has to be changed. Summarily, the steps of the algorithm are [20] :
1) Initializing the starting state of the coin and node register in an equal weight superposition. This can be done by applying Hadamard gate on each qubit of the state
2) Applying quantum random walk search iteration 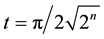
The steps of the quantum random walk search iteration are:
a) Applying a quantum oracle;
b) Applying an appropriate coin depending on the state of the control register;
c) Applying the quantum oracle;
d) Applying the shift operator.
Due to the symmetry of the hypercube, its nodes can always be re-labeled in such way that the marked node 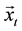
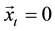
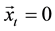
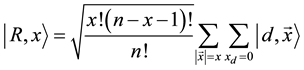
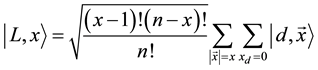
The shift operator in this collapsed random walk basis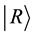
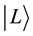
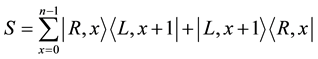
The quantum random walk on a line strongly depends on the position. In the basis
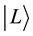
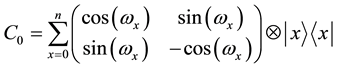
where 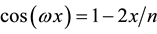

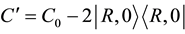
4. Algorithm with Coins from Generalized Householder Reflection
Potocek et al. have shown in [17] that if the register is divided into two subspaces―for even and for odd elements?by the shift operator, they can both evolve separately. Thus, the probability to find a solution increases twofold.
In this chapter it will be demonstrated that the same result can also be obtained by using appropriate coins.
4.1. Generalized Householder Reflection
The generalized Householder reflection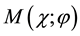
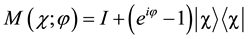
where 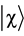
Figure 1. Quantum circuit for random walk search algorithm. The box marked as T is the random walk search iteration and shoud be repeated t times. The value of t is shown in Section 3.
Figure 2. Projecting random walk search algorithm on a hypercube to a random walk on a line. The marked state is shown with orange.
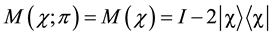
In [16] , the case is discussed when C0 is again an equal superposition vector, but the phase is random. In this paper, only Householder reflection with phase equal to π will be discussed, when 
4.2. General Form of the Coins
Here we will view the case when C0 is a standard Grover coin, as it is in the original SKW search algorithm:
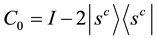
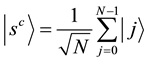
where 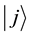

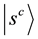
For the marking coin C1, an arbitrary Householder reflection is taken with a phase π:
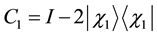
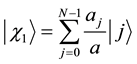
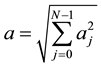
here aj is real and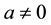
The coin and the random walk step are unchanged, as in the standard SKW search algorithm:
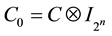
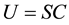
The perturbed random walk coin is:


This form is too general, so in the next subsection some examples for coins will be discussed.
4.3. Algorithm
The steps of this implementation of QRWS are the same as in the SKW search algorithm. The quantum circuit of this algorithm is almost the same as in SKW and is shown in Figure 1, the difference being that the marking coin is different and an additional qubit is taken which does not need to be measured at the end of the algorithm.
4.4. Examples for Some Good Coins
Some examples of coins suitable for a random walk search are proposed in this section. These examples are probably not only the useful ones but also can be performed relatively easily in experiments. A Householder reflection can easily be done with an N-pod system.
For simplicity, a hypercube with dimension 2K, instead of a hypercube with dimension N will be reviewed.
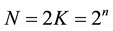
From here on, yi will denote arbitrary values, and yi may or may not be equal to yj at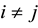
One case of asymmetrical coins is when
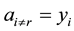
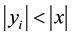
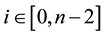
In the first searched subspace, the coin marks the element marked by the oracle. In the second searched subspace, the marking coin effectively marks one of the adjacent nodes. The matrix chosen to be used in the marking coin defines which of the nodes is marked. The division of the searched space in two requires an additional qubit (the number of states of the register prior to the division is 2K) in order to perform the search and to have a probability of finding a solution above 80%.
Here are two examples of such coins, depending on the way of doubling the number of states by adding a qubit:
The first type of such coin is when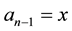
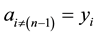
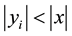
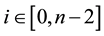

This result can easily be explained when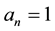

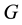
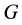
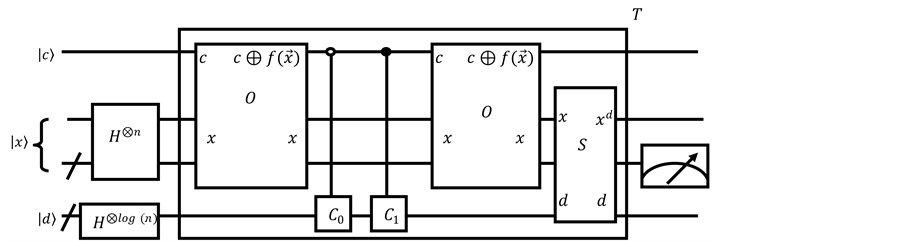
The number of steps needed depends on the exact values of x and yi. The quantum circuit needed for those types of coins is shown in Figure 5.

Figure 3. Difference between uses of a marking coin in: (a) SKW search algorithm on a hypercube; (b) Standard walk on hypercube of Grover Coin with no marked state; (c) Implementation of walk with generalized Householder reflection coin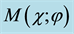
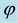


Figure 4. The simplest case is when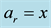
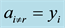

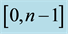
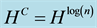
The simulations are made by two qubit coins because of the absence of enough computational power to make simulations for coins with more qubits.
Values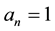
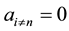
With two-qubit coins, 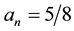
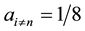
Figure 5. Quantum circuit for coins when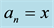
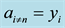
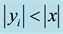
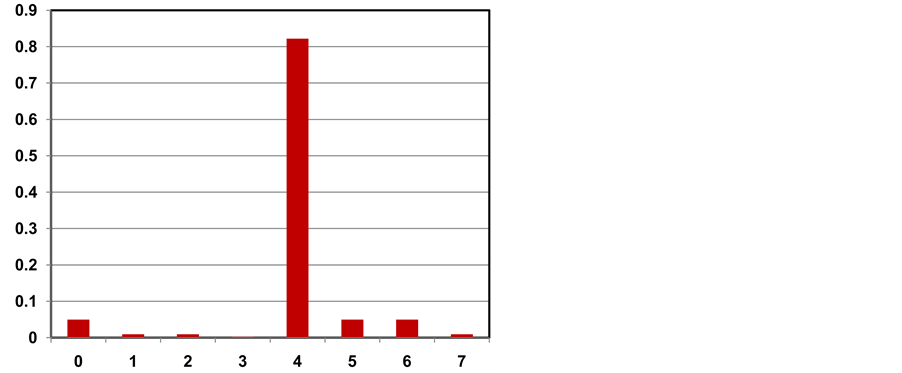
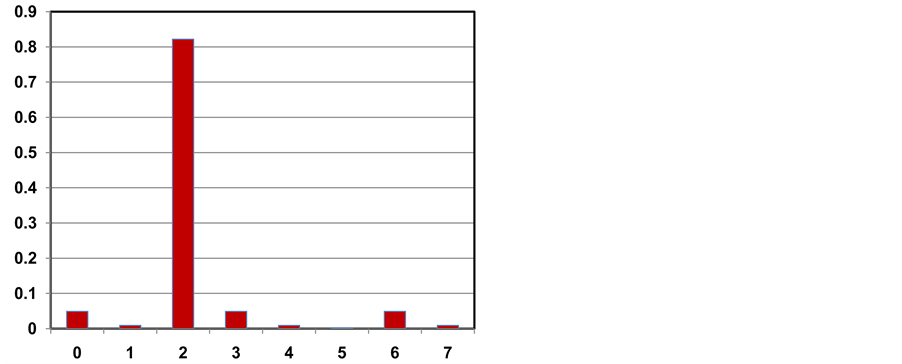
Figure 6. Result of simulating a quantum circuit with a coin with 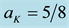
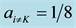
It has been obtained by numerical simulations that a higher probability of finding the searched element is achieved when 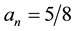
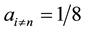
Another type of such coin is the case when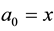

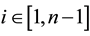
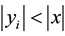
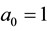
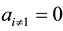
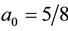
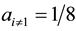
When 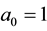
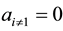
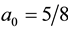
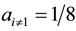

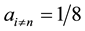
With all other cases having this structure of the coin, when
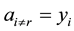
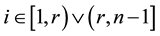
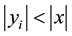
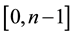
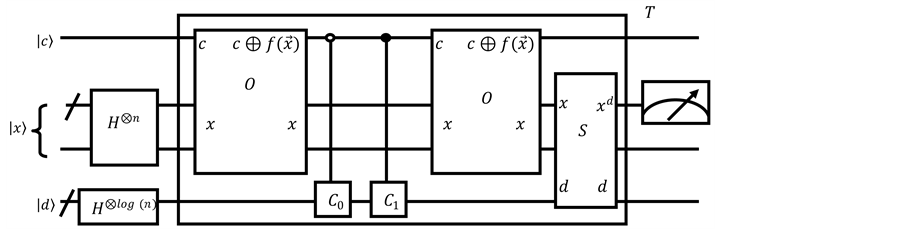
Numerical simulations show that at least when the size of the node register N = 16, there are also other coins with different shape of the vector 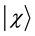
Examples for such coins are when
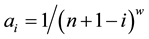
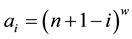
Figure 7. Quantum circuit for coins when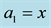
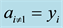
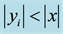
Figure 8. Result of the simulation of the quantum circuit with a coin with 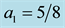
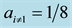

and when
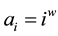
An example for such coins is when the formula (28) is used with the quantum circuit shown in Figure 5. The probability for finding a solution is approximately 0.77, with w = 3.
Another example of search coin is when the formula (26) is used with the quantum circuit shown in Figure 7. The probability for finding a solution is approximately 0.77, with w = 3.
The number of steps needed for the coins showed in this section is obtained by numerical simulations and has not been found empirically yet.
5. Conclusions
A discrete quantum random walk search algorithm optimized for hypercube is discussed. A new alternative DTRWS method for dividing the searched space in two is presented. The searched space is divided effectively into two by using asymmetric coins, which distribute the probability of shifting into neighboring nodes non-un- iformly.
The advantage of this method is that it preserves the topology of the hypercube and does not divide it by modifying the shift operator. The coins are obtained by using Householder reflection, which can be easily performed in experiments by using N-pod systems.
References
- Grover, L. (1996) A Fast Quantum Mechanical Algorithm for Database Search. arXiv:/9605043 [quant-ph].
- Yamaguchi, F., Milman, P., Brune, M., Raimond, J. and Haroche, S. (2002) Quantum Search with Two-Atom Collisions in Cavity QED. Physical Review A, 66, Article ID: 010302. arXiv:quant-ph/0203146v1. http://dx.doi.org/10.1103/PhysRevA.66.010302
- Vandersypen, L., Steffen, M., Sherwood, M., Yannoni, C., Breyta, G., and Chuang, I. (2000) Implementation of a Three- Quantum-Bit Search Algorithm. Applied Physics Letters, 76, 646-648. arXiv:quant-ph/9910075v2. http://dx.doi.org/10.1063/1.125846
- Gent, I. and Walsh, T. (1994) Easy Problems Are Sometimes Hard. Artificial Intelligence, 70, 335-345. http://dx.doi.org/10.1016/0004-3702(94)90109-0
- Sze, S. and Pevzner, P. (1997) Las Vegas Algorithms for Gene Recognition: Suboptimal and Error-Tolerant Spliced Alignment. RECOMB’97 Proceedings of the 1st Annual International Conference on Computational Molecular Biology, Santa Fe, 20-23 January 1997, 300-309. http://dx.doi.org/10.1145/267521.267889
- Clark, M. and Kennedy, A. (2007) Accelerating Dynamical-Fermion Computations Using the Rational Hybrid Monte Carlo Algorithm with Multiple Pseudofermion Fields. Physical Review Letters, 98, Article ID: 051601. http://dx.doi.org/10.1103/PhysRevLett.98.051601
- Newman, M. and Ziff, R. (2001) Fast Monte Carlo Algorithm for Site or Bond Percolation. Physical Review E, 64, Article ID: 016706. http://dx.doi.org/10.1103/PhysRevE.64.016706
- Houdayer, J. (2001) A Cluster Monte Carlo Algorithm for 2-Dimensional Spin Glasses. The European Physical Journal B―Condensed Matter and Complex Systems, 22, 479-484. arXiv:condmat/0101116 [cond-mat.dis-nn].
- Farhi, E. and Gutmann, S. (1998) Quantum Computation and Decision Trees. Physical Review A, 58, 915-928. http://dx.doi.org/10.1103/PhysRevA.58.915
- Childs, A., Farhi, E. and Gutmann, S. (2001) An Example of the Difference between Quantum and Classical Random Walks. Quantum Information Processing, 1, 35-43. arXiv:quantph/0103020.
- Childs, A., Cleve, R., Deotto, E., Farhi, E., Gutmann, S. and Spielman, D.A. (2002) Exponential Algorithmic Speedup by Quantum Walk. arXiv:quant-ph/0209131v2.
- Childs, A. and Goldstone, J. (2004) Spatial Search by Quantum Walk. Physical Review A, 70, Article ID: 022314. arXiv:quant-ph/0306054v2. http://dx.doi.org/10.1103/PhysRevA.70.022314
- Aharonov, Y., Davidovich, L. and Zagury, N. (1993) Quantum Random Walks. Physical Review A, 48, 1687-1690. http://dx.doi.org/10.1103/PhysRevA.48.1687
- Ambainis, A. (2003) Quantum Walk Algorithm for Element Distinctness. arXiv:quant-ph/0311001.
- Shenvi, N., Kempe, J. and Whaley, K. (2003) Quantum Random-Walk Search Algorithm. Physical Review A, 67, Article ID: 052307. http://dx.doi.org/10.1103/PhysRevA.67.052307
- Hein, B. and Tanner, G. (2009) Quantum Search Algorithms on the Hypercube. Journal of Physics A: Mathematical and Theoretical, 42, Article ID: 085303. arXiv:0906.3094v1 [quant-ph]. http://dx.doi.org/10.1088/1751-8113/42/8/085303
- Potocek, V., Gabris, A., Kiss, T. and Jex, I. (2009) Optimized Quantum Random-Walk Search Algorithms on the Hy- percube. Physical Review A, 79, Article ID: 012325. http://dx.doi.org/10.1103/PhysRevA.79.012325
- Tulsi, A. (2008) Faster Quantum Walk Algorithm for the Two Dimensional Spatial Search. Physical Review A, 78, Article ID: 012310. arXiv:0801.0497v2 [quant- ph].
- Long, G. (2001) Grover Algorithm with Zero Theoretical Failure Rate. Physical Review A, 64, Article ID: 022307. http://dx.doi.org/10.1103/PhysRevA.64.022307
- Hoyer, S. (2008) Quantum Random Walk Search on Satisfiability Problems. PhD Thesis, Swarthmore College, Swar- thmore.
- Ambainis, A., Kempe, J. and Rivosh, A. (2004) Coins Make Quantum Walks Faster. arXiv:quantph/0402107.
- Nayak, A. and Vishwanath, A. (2000) Quantum Walk on the Line. arXiv:quant-ph/0010117v1.
- Kempe, J. (2003) Quantum Random Walks―An Introductory Overview. Contemporary Physics, 44, 307-327. arXiv:quant-ph/0303081. http://dx.doi.org/10.1080/00107151031000110776