Journal of Quantum Information Science
Vol.4 No.1(2014), Article ID:42934,4 pages DOI:10.4236/jqis.2014.41002
Virtual Numbers to Represent Entangled Quantum States
Lalit A. Patel
17892 Linda Drive, Yorba Linda, California, USA
Email: Laxmlit@att.net
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 22 October 2013; revised 17 January 2014; accepted 7 February 2014
ABSTRACT
In the existing formalism of quantum states, probability amplitudes of quantum states are complex numbers. A composition of entangled quantum states, such as a Bell state, cannot be decomposed into its constituent quantum states, implying that quantum states lose their identities when they get entangled. This is contrary to the observation that a composition of entangled quantum states decays back to its constituent quantum states. To eliminate this discrepancy, this paper introduces a new type of numbers, called virtual numbers, which produce zero upon multiplication with complex numbers. In the proposed formalism of quantum states, probability amplitudes of quantum states are general numbers made of complex and virtual numbers. A composition of entangled quantum states, such as a Bell state, can then be decomposed into its constituent quantum states, implying that quantum states retain their identities when they get entangled.
Keywords:Quantum Mechanics; Probability Amplitude; Complex Number; Entanglement; Bell State

1. Introduction
Deutsch [1] , Shor [2] , and Grover [3] algorithms demonstrated the computational power of quantum states and led to the subject of quantum information science. Recently there has been a lot of research and development related to quantum algorithms, quantum computing, and quantum communication [4] . To avoid incorrect theories in these subjects, it is necessary to have a reliable formalism of quantum states.
In the existing formalism of quantum states, probability amplitudes of quantum states are complex numbers. A composition of entangled quantum states, such as a Bell state [5] , cannot be decomposed into its constituent quantum states, implying that quantum states lose their identities when they get entangled. This is contrary to the observation that a composition of entangled quantum states decays back to its constituent quantum states.
To eliminate this discrepancy, this paper introduces a new type of numbers, called virtual numbers, which produce zero upon multiplication with complex numbers. In the proposed formalism of quantum states, probability amplitudes of quantum states are general numbers made of complex and virtual numbers. A composition of entangled quantum states, such as a Bell state, can then be decomposed into its constituent quantum states, implying that quantum states retain their identities when they get entangled.
2. Complex Amplitudes
A qubit is a quantum bit of a two-level system governed by the quantum superposition principle. Using Dirac’s bra and ket notations, two qubits may be represented as:
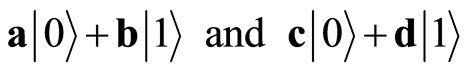 (1)
(1)
Here 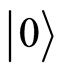 and
and 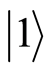 denote ground and excited states. a, b, c, and d are probability amplitudes, which satisfy the normalization conditions:
denote ground and excited states. a, b, c, and d are probability amplitudes, which satisfy the normalization conditions:
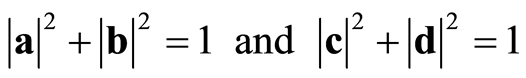 (2)
(2)
In the existing formalism, the probability amplitudes a, b, c, and d are complex numbers.
If the two qubits of Equation (1) are composed together, the resultant system becomes:
 (3)
(3)
Now consider a reverse problem. Suppose a mixture of qubits is given as:
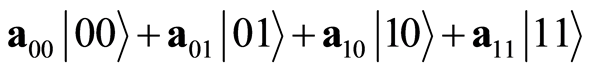 (4)
(4)
It is desired to decompose this mixture of qubits into its constituent qubits.
Different scenarios arise here depending on the probability amplitudes (a00, a01, a10, and a11) in Equation (4). If all four probability amplitudes are non-zero and can be uniquely factored, the mixture can be decomposed into its constituent qubits, which can be designated as in Equation (1). On the other hand, if one or two probability amplitudes are zero and/or if the four probability amplitudes cannot be uniquely factored, it is not possible to decompose the mixture into its constituent qubits. In this case, the constituent qubits are said to be entangled.
A special case of Equation (4) is a Bell state represented as:
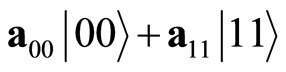 (5)
(5)
Here a00 and a11 are some given constants. If the constituent qubits are to be given by Equation (1), equations to be solved for are:
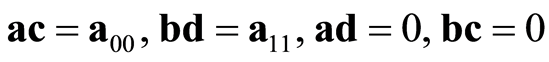 (6)
(6)
This equation has no solution in terms of complex numbers.
The fact that the mixture represented by Equation (5) cannot be factored into its constituent qubits implies that the constituent qubits have lost their identities after getting entangled. This is contrary to the observation that a composition of entangled quantum states decays back to its constituent quantum states.
3. Virtual Numbers
The fact that Equation (6) has no solution in terms of complex numbers implies that the existing set of complex numbers is inadequate to solve equations such as Equation (6). However, as described in the following, it is possible to solve Equation (6) by introducing a new type of numbers as an add-on to the set of complex numbers.
A new type of numbers, called virtual numbers, is now introduced as follows.
1) A general number is made by adding a complex number and a virtual number.
2) A virtual number is made by prefixing a complex number with an exclamation mark “!”.
3) Multiplication of a complex number and a virtual number produces zero.
4) Multiplication of two virtual numbers produces a complex number, equal to the multiplication of complex number values of the virtual numbers.
Thus, if a, b, c, and d are some complex numbers, !b and !d are virtual numbers, and (a + !b) and (c + !d) are general numbers, and their multiplication gives:
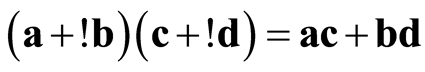 (7)
(7)
According to Equation (7), a general number may be interpreted as a two-dimensional vector, with complex and virtual parts of the general number as the magnitudes of the vector along the two axes, and multiplication of two general numbers may be interpreted as a dot product of two vectors formed by the two general numbers.
4. Virtual Amplitudes
It is now proposed that probability amplitudes of quantum states can be general numbers (made of complex and virtual numbers) instead of only complex numbers.
Consider two quantum states:
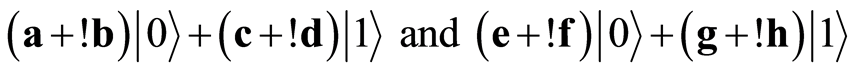 (8)
(8)
The four probability amplitudes of these two quantum states are general numbers, which contain complex numbers (a, c, e, g) and virtual numbers (!b, !d, !f, !h).
According to the definition of virtual numbers, a composition of these two quantum states is:
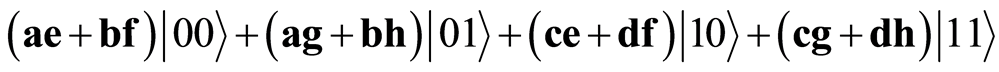 (9)
(9)
Under this new formalism, it is now possible to solve Equation (6).
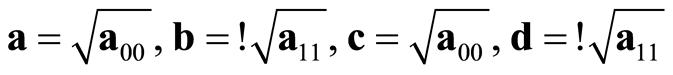 (10)
(10)
It is possible to decompose the Bell state of Equation (5) as:
 (11)
(11)
The composition of these quantum states does not lead to  and
and  qubits because of the presence of !.
qubits because of the presence of !.
Thus, under this new formalism, a composition of entangled quantum states (such as a Bell state) can be decomposed into its constituent quantum states, which implies that quantum states retain their identities when they get entangled.
5. Alternative Approach
In order to enable decomposition of a Bell state into its constituent quantum states, Beil [6] proposed a matrix formalism for probability amplitudes of quantum states. The matrix formalism proposed by Beil is an alternative to the virtual-numbers formalism proposed in this paper.
Advantage of Beil’s approach is that it does not require changes in the Number theory; disadvantage is that it requires changes in the Quantum theory. Advantage of this paper’s approach is that it does not require changes in the Quantum theory; disadvantage is that it requires changes in the Number theory.
Auletta [7] has discussed some other issues related to quantum computation.
6. Conclusion
The proposed formalism for quantum states in terms of virtual numbers enables decomposition of an otherwise un-decomposable mixture of entangled quantum states. It can explain the observation that the constituent quantum states of such a mixture retain their identities after they get entangled. By using this formalism instead of the existing formalism, it is possible to avoid incorrect theories in quantum algorithms, quantum computing, and quantum communication.
References
- Deutsch, D. (1985) Quantum Theory: The Church-Turing Principle and the Universal Quantum Computer. Proceedings of the Royal Society of London, A400, 97-117. http://rspa.royalsocietypublishing.org/content/400/1818/97.abstract
- Shor, P.W. (1994) Algorithms for Quantum Computation: Discrete Log and Factoring. Foundations of Computer Science, 1994, 124-134. http://www.computer.org/csdl/proceedings/focs/1994/6580/00/0365700-abs.html
- Grover, L.K. (1997) Quantum Computers Can Search Arbitrarily Large Databases by a Single Query. Physical Review Letters, 79, 4709-4712. http://dx.doi.org/10.1103/PhysRevLett.79.4709
- Nielsen, M.A. and Chuang, I.L. (2011) Quantum Computation and Quantum Information. University Press, Cambridge.
- Bell, J.S. (1964) On the Einstein-Podolsky-Rosen Paradox. Physics, 1, 195-200.
- Beil, C. (2013) Quantum Entanglement, Emergence, and Noncommutative Blowups. http://arxiv-web3.library.cornell.edu/pdf/1310.5673v1.pdf
- Auletta, G. (2013) A New Way to Implement Quantum Computation. Journal of Quantum Information Science, 3, 127-137. http://dx.doi.org/10.4236/jqis.2013.34017

