Journal of Quantum Information Science
Vol.2 No.2(2012), Article ID:20135,5 pages DOI:10.4236/jqis.2012.22005
Dependence of Entanglement on Initial States under Amplitude Damping Channel in Non-Inertial Frames
Key Laboratory of Low-dimensional Quantum Structures and Quantum Control of Ministry of Education, Department of Physics, Hunan Normal University, Changsha, China
Email: *jljing@hunnu.edu.cn
Received January 13, 2012; revised March 16, 2012; accepted April 10, 2012
Keywords: Entanglement; Initial States; Amplitude Damping Channel
ABSTRACT
Under amplitude damping channel, the dependence of the entanglement on the initial states 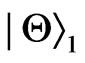 and
and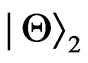 , which reduce to four orthogonal Bell states if we take the parameter of states
, which reduce to four orthogonal Bell states if we take the parameter of states 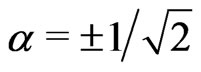 are investigated. We find that the entanglements for different initial states will decay along different curves even with the same acceleration and parameter of the states. We note that, in an inertial frame, the sudden death of the entanglement for
are investigated. We find that the entanglements for different initial states will decay along different curves even with the same acceleration and parameter of the states. We note that, in an inertial frame, the sudden death of the entanglement for 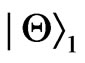 will occur if
will occur if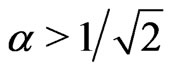 , while it will not take place for
, while it will not take place for 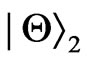 for any α. We also show that the possible range of the sudden death of the entanglement for
for any α. We also show that the possible range of the sudden death of the entanglement for  is larger than that for
is larger than that for . There exist two groups of Bell state here we can’t distinguish only by concurrence.
. There exist two groups of Bell state here we can’t distinguish only by concurrence.
1. Introduction
In the theory of quantum information, entanglement, a very subtle phenomenon, has been investigated many years since it was first brought to light by Einstein, Podolsky and Rosen [1], and by Schrödinger [2,3]. It took about 30 years to distinguish it from classical physics by Bell [4], and it was also found that the entanglement plays a key role in quantum computation algorithms [5]. To the best of our knowledge, the early studies were just confined to isolated system. However, anything can be thought of as being encompassed by its environment which may influences its dynamics, so the study of entanglement in an open systems is imperative. Some inchoate ideas about this topic were presented in quantum optics [6]. On the other hand, with the rise of relativistic quantum information, much attention has been concentrated on the behavior of quantum correlations in a relativistic setting [7-12]. These works provide us some new way in understanding the quantum theory. Recently, the decoherence in noninertial frame has been first discussed under a noise environment [13] also.
It is well known that the Bell state is a concept in quantum information science and represents the simplest possible examples of entanglement. And there are four orthogonal Bell states
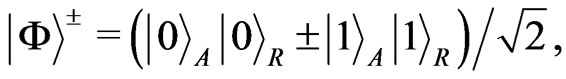
 (1)
(1)
where 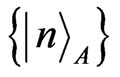 indicate Minkowski modes described by Alice and
indicate Minkowski modes described by Alice and 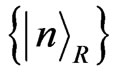 described by Rob, respectively. Sibasish Ghosh showed that it is not possible to discriminate between any three Bell states if only a single copy is provided and if only local operations and classical communication are allowed [14]. At present most of the studies consider only one of the Bell states but ignore the other three [9-13,15,16] because different Bell states will give the same result without considering environment. On the other hand, Philip Walther and Anton Zeilinger realized a probabilistic for Bell state analyzer for two photonic quantum bits by use of a non-destructive controlled-NOT gate based on entirely linear optical elements [17]. And Miloslav Dusek showed that with no auxiliary photons it is impossible to discriminate Bell states without errors and it is impossible to discriminate such Bell states with certainty in any way by the means of linear optics [18]. Along the way, it is natural to ask whether the entanglement is related to the initial (Bell) states if we introduce environment? In this paper, we will address this question by studying concurrence when both subsystems are coupled to a noise environment. For the sake of universality, we take two general initial states
described by Rob, respectively. Sibasish Ghosh showed that it is not possible to discriminate between any three Bell states if only a single copy is provided and if only local operations and classical communication are allowed [14]. At present most of the studies consider only one of the Bell states but ignore the other three [9-13,15,16] because different Bell states will give the same result without considering environment. On the other hand, Philip Walther and Anton Zeilinger realized a probabilistic for Bell state analyzer for two photonic quantum bits by use of a non-destructive controlled-NOT gate based on entirely linear optical elements [17]. And Miloslav Dusek showed that with no auxiliary photons it is impossible to discriminate Bell states without errors and it is impossible to discriminate such Bell states with certainty in any way by the means of linear optics [18]. Along the way, it is natural to ask whether the entanglement is related to the initial (Bell) states if we introduce environment? In this paper, we will address this question by studying concurrence when both subsystems are coupled to a noise environment. For the sake of universality, we take two general initial states
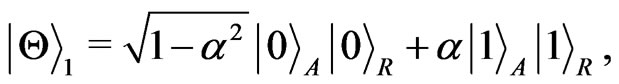 (2)
(2)
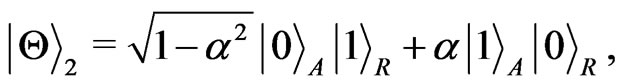 (3)
(3)
where .
. 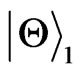 can degrade into the Bell states
can degrade into the Bell states 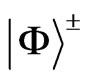 and
and 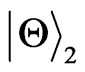 into
into  if we take
if we take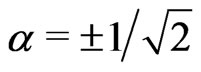 , respectively. Then, we can find that the behavior of the entanglement will be greatly influenced by initial states, but we can only distinguish the initial states
, respectively. Then, we can find that the behavior of the entanglement will be greatly influenced by initial states, but we can only distinguish the initial states 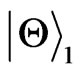 (or
(or ) from
) from 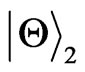 (or
(or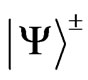 ).
).
In this paper, we will investigate the dependence of the entanglement on the initial states which reduce to four orthogonal Bell states under amplitude damping channel. We will show that the entanglements for different initial states will decay along different curves even with the same acceleration and parameter of the states, and the possible range of the sudden death of the entanglement for 1 is larger than that for 2.
This paper is structured as follows. In Section 2 we will study the concurrence when both of the qubits under amplitude damping channel using the initial state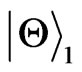 . In Section 3 we will consider the concurrence when both of the qubits under the same environment by taking the state
. In Section 3 we will consider the concurrence when both of the qubits under the same environment by taking the state . Our work will be summarized in last section.
. Our work will be summarized in last section.
2. Entanglement for Initial States 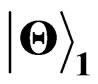
We first study the entanglement for initial states . We assume two observers, Alice who stays stationary has a detector only sensitive to mode
. We assume two observers, Alice who stays stationary has a detector only sensitive to mode 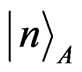 and Rob who moves with a uniform acceleration has a detector which can only detect mode
and Rob who moves with a uniform acceleration has a detector which can only detect mode , share a entangled initial state
, share a entangled initial state 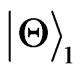 at the same point in Minkowski spacetime. We can use a two-mode squeezed state to expend the Minkowski vacuum from the perspective of Rob[8]
at the same point in Minkowski spacetime. We can use a two-mode squeezed state to expend the Minkowski vacuum from the perspective of Rob[8] 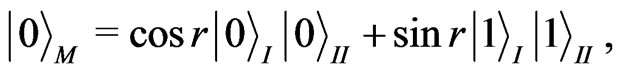 where
where 
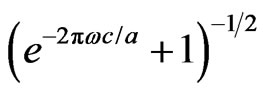 , a is Rob’s acceleration, ω is energy of the Dirac particle, c is the speed of light in vacuum, and
, a is Rob’s acceleration, ω is energy of the Dirac particle, c is the speed of light in vacuum, and 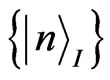 indicate Rindler modes in region I and
indicate Rindler modes in region I and 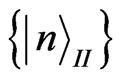 indicate Rindler modes in region II, respectively. And the only excited state can be given by
indicate Rindler modes in region II, respectively. And the only excited state can be given by 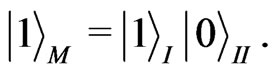 Thus, we can rewrite Equation (2) in terms of Minkowski modes for Alice and Rindler modes for Rob
Thus, we can rewrite Equation (2) in terms of Minkowski modes for Alice and Rindler modes for Rob
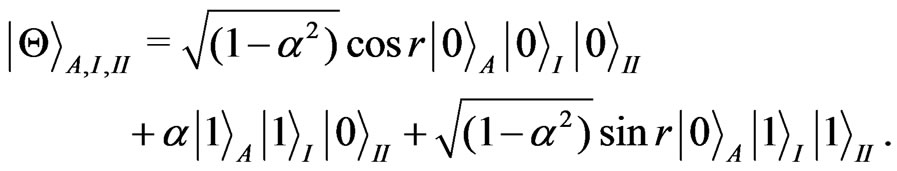 (4)
(4)
On account of Rob is causally disconnected from region II, and tracing over the states in region II, we obtain
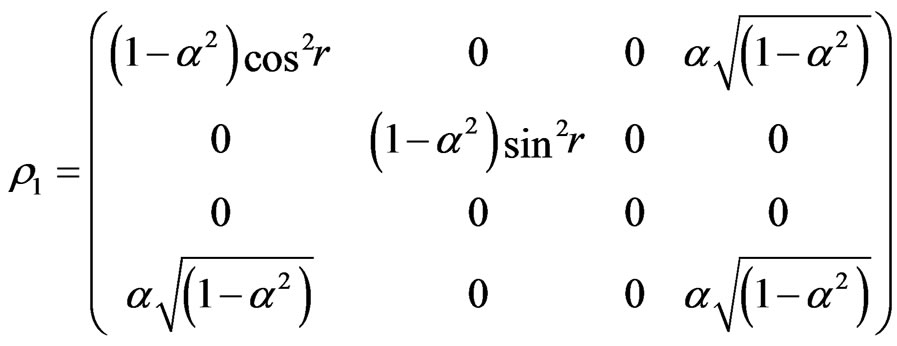
We now let both Rob and Alice interact with a amplitude damping environment [19]. There is a simple way to understand this process if we use the quantum map [20,21]
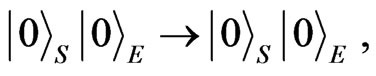 (5)
(5)
 (6)
(6)
Equation (5) shows that if the system stays 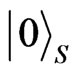 both it and its environment will not change at all. Equation (6) indicates that if the system stays
both it and its environment will not change at all. Equation (6) indicates that if the system stays 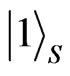 the decay will exist in the system with probability P, and it can also remain there with probability (1 – P).
the decay will exist in the system with probability P, and it can also remain there with probability (1 – P).
If the environment acts independently on Alice’s and Rob’s states, the total evolution of these two qubits system can be expressed as [15]

where 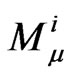 are the Kraus operators
are the Kraus operators
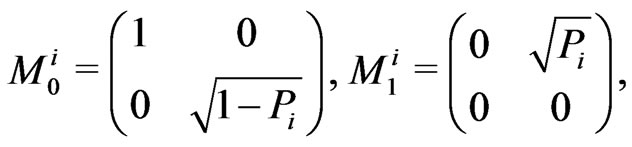 (7)
(7)
where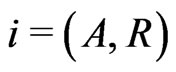 , PA is the decay parameter in Alice’s quantum channel and PR is the decay parameter in Rob’s quantum channel, and Pi
, PA is the decay parameter in Alice’s quantum channel and PR is the decay parameter in Rob’s quantum channel, and Pi  is a parameter relating only to time. Under the Markov approximation, the relationship between the parameter Pi and the time t is given by
is a parameter relating only to time. Under the Markov approximation, the relationship between the parameter Pi and the time t is given by 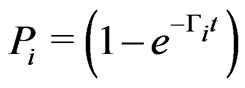 [15,19], where
[15,19], where 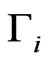 is the decay rate. We must note that here we just consider the local channels [15], in which all the subsystems interact independently with its own environment and no communication appears. i.e.,
is the decay rate. We must note that here we just consider the local channels [15], in which all the subsystems interact independently with its own environment and no communication appears. i.e.,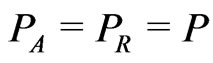 . Then we can obtain the evolved states in this case (see Equation (8))where
. Then we can obtain the evolved states in this case (see Equation (8))where  and
and . Since it is well known that the degree of entanglement for a two-qubits mixed state in noisy environments can be quantified very conveniently by the concurrence [22,23]
. Since it is well known that the degree of entanglement for a two-qubits mixed state in noisy environments can be quantified very conveniently by the concurrence [22,23]
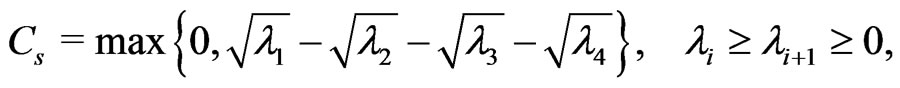
 (8)
(8)
where 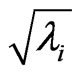 are square roots of the eigenvalues of the matrix
are square roots of the eigenvalues of the matrix , with
, with 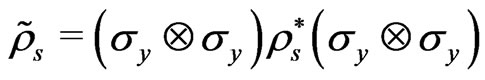 is the “spin-flip” matrix for the state (5). So, we obtain the concurrence as a function of α, r and P
is the “spin-flip” matrix for the state (5). So, we obtain the concurrence as a function of α, r and P
 (9)
(9)
Due to the concurrence is just depended on  and
and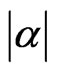 , we can’t distinguish the initial states described by
, we can’t distinguish the initial states described by 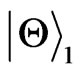 with
with 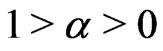 or
or .
.
3. Entanglement for Initial States 
Now, we consider the other initial state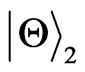 . Using the same method as mentioned above we obtain its density matrix
. Using the same method as mentioned above we obtain its density matrix

and the evolved state for 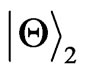
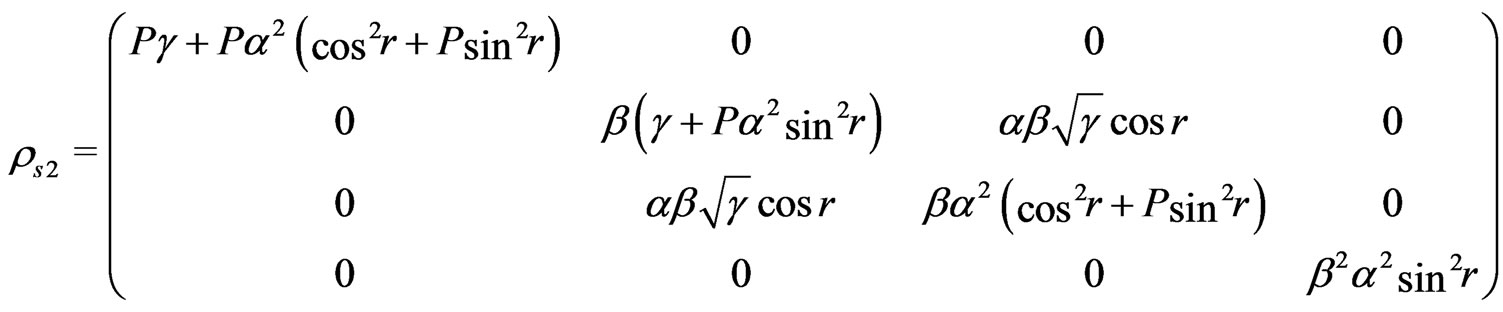 (10)
(10)
Thus, the concurrence is
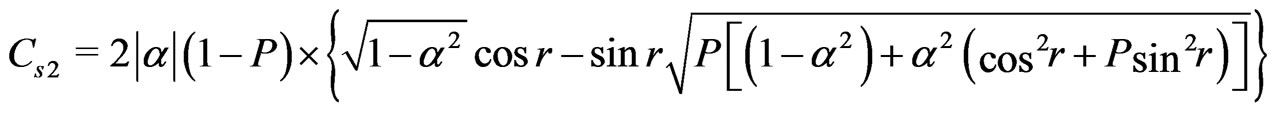 (11)
(11)
From which we know that we can’t distinguish the initial states described by 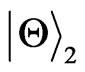 with
with 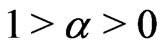 or
or 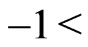

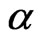 , too.
, too.
4. Discussions and Conclusions
By comparing Equations. (10) and (13), we can see that there are obvious differences between 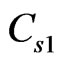 and
and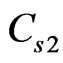 . Especially, we find that
. Especially, we find that 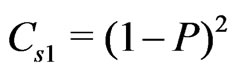 and
and 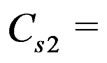
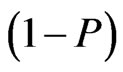 for Bell states
for Bell states 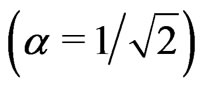 in an inertial frame.
in an inertial frame.
But if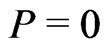 , we have
, we have 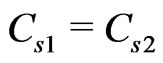 for any r and α, which means that the two groups of the initial states will be equivalent without the effect of environment.
for any r and α, which means that the two groups of the initial states will be equivalent without the effect of environment.
To learn the behavior of the entanglement intuitively, we plot the concurrence for different initial states 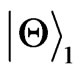 and
and 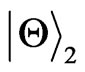 with different parameters in Figure 1. From the left two panels we find that, in an inertial frame (i.e.,
with different parameters in Figure 1. From the left two panels we find that, in an inertial frame (i.e., ), the
), the  will tend to zero for a finite time which is called sudden death if
will tend to zero for a finite time which is called sudden death if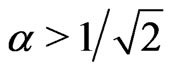 . However, the
. However, the 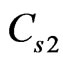 will not tend to zero for any α and it will decay along the same curve for both α and its normalized partner
will not tend to zero for any α and it will decay along the same curve for both α and its normalized partner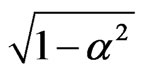 , which shows us that we can’t discriminate Alice’s excited states from Rob’s excited states for initial states
, which shows us that we can’t discriminate Alice’s excited states from Rob’s excited states for initial states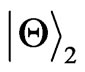 , i.e., α and
, i.e., α and 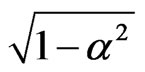 will lead to a symmetrical structure at
will lead to a symmetrical structure at 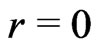 for initial states
for initial states . We also note that the concurrences for
. We also note that the concurrences for  and
and 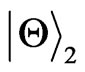 decay different from each other even they have the same α.
decay different from each other even they have the same α.
From Figure 1, if we fix α, it is easy to find out that, as r becomes large which means the increase of the Rob’s acceleration, the sudden death of the entanglement for both  and
and 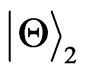 would happen earlier and earlier. That is to say, a bigger acceleration leads to a faster decay of the entanglement, in another word, the stronger Unruh effect will speed the decay of entanglement. On the other hand, if we fix r, we find that the entanglement decay faster and faster as the α increases except a special case for
would happen earlier and earlier. That is to say, a bigger acceleration leads to a faster decay of the entanglement, in another word, the stronger Unruh effect will speed the decay of entanglement. On the other hand, if we fix r, we find that the entanglement decay faster and faster as the α increases except a special case for 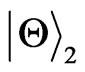 with
with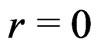 . For the states
. For the states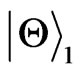 , the more the initial excited states there are, the stronger is the interaction between the system with environment, which will lead to a faster disappear of the entanglement. For the states
, the more the initial excited states there are, the stronger is the interaction between the system with environment, which will lead to a faster disappear of the entanglement. For the states , although the total number of the excited states keeps conservable whatever α is, the time of sudden death can also change with α because the proportion of Alice’s excited states and Rob’s excited states affects the decay velocity.
, although the total number of the excited states keeps conservable whatever α is, the time of sudden death can also change with α because the proportion of Alice’s excited states and Rob’s excited states affects the decay velocity.
If the parameters r, α and P in Equation (10) satisfy the relation
 (12)
(12)
we have , and if the parameters r, α and P in Equation (13) meet
, and if the parameters r, α and P in Equation (13) meet
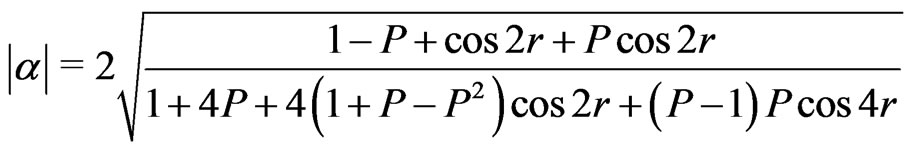 we obtain
we obtain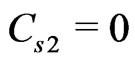 . Using Equations (14) and (15) (See Figure 2), we can find a possible range for the sudden death of the entanglement. In consideration of
. Using Equations (14) and (15) (See Figure 2), we can find a possible range for the sudden death of the entanglement. In consideration of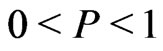 , for the states
, for the states , we find that the sudden death of the entanglement will appear if α satisfy the relation
, we find that the sudden death of the entanglement will appear if α satisfy the relation
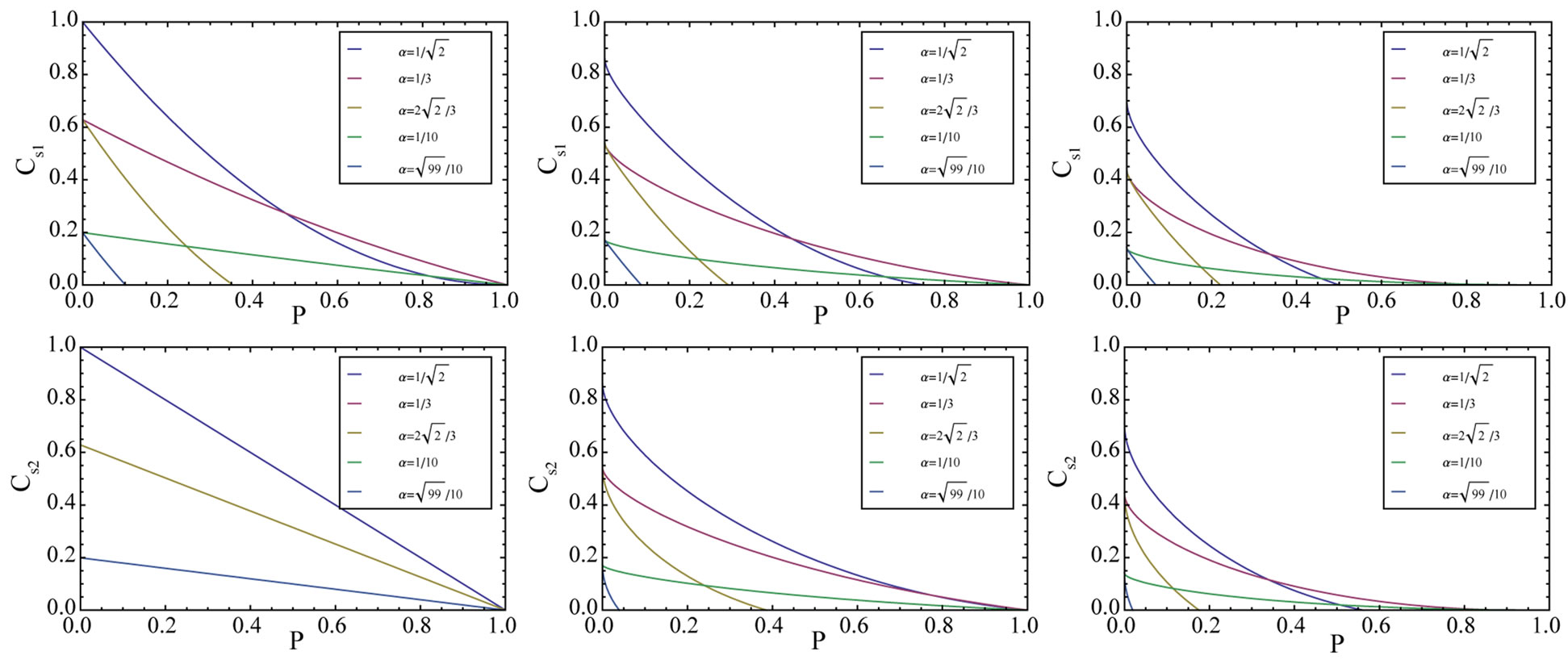
Figure 1. (Color online) Concurrence for the initial states  (first row) and
(first row) and  (second row) as a function of P with some fixed initial state parameters α and acceleration parameters r = 0 (left), r = π/6 (middle) and r = π/4 (right) when both qubits are coupled to the same noise environment.
(second row) as a function of P with some fixed initial state parameters α and acceleration parameters r = 0 (left), r = π/6 (middle) and r = π/4 (right) when both qubits are coupled to the same noise environment.

Figure 2. (Color online) The grid surface presents the possible range of the sudden death for the initial states  (left) and
(left) and  (right) when both qubits are coupled to a noise environment.
(right) when both qubits are coupled to a noise environment.
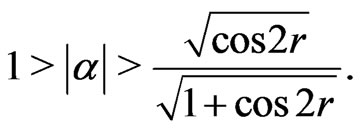 (13)
(13)
And for the states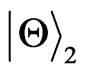 , the sudden death of entanglement can happen only when
, the sudden death of entanglement can happen only when
 (14)
(14)
It is obviously that the possible range of the sudden death of the entanglement for  is larger than that for
is larger than that for . If
. If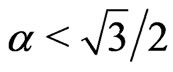 , whatever r is, the disappear of the entanglement for
, whatever r is, the disappear of the entanglement for  will be earlier than that for
will be earlier than that for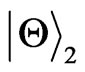 .
.
Above discussions reveal some different behaviors of concurrences for the initial states 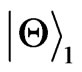 and
and  when both subsystems are coupled to noise environment. Thus, the entanglement is dependent to the initial states under the amplitude damping channel.
when both subsystems are coupled to noise environment. Thus, the entanglement is dependent to the initial states under the amplitude damping channel.
5. Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant No. 11175065, 10935013; the SRFDP under Grant No. 20114306110003; PCSIRT, No. IRT0964; the Hunan Provincial Natural Science Foundation of China under Grant No. 11JJ7001; and the Construct Program of the National Key Discipline.
REFERENCES
- A. Einstein, B. Podolsky and N. Rosen, “Can QuantumMechanical Description of Physical Reality Be Considered Complete?” Physical Review, Vol. 47, No. 10, 1935, p. 777.
- E. Schrödinger, “Die gegenwartige Situation in der Quantenmechanik,” Naturwissenschaften, Vol. 23, No. 48, 1935, pp. 823-828.
- E. Schrödinger, “Probability Relations between Separated Systems,” Proceedings of the Cambridge Philosophical Society, Vol. 32, No. 3, 1936, p. 446.
- J. S. Bell, “On the Einstein Podolsky Rosen Paradox,” Physics, Vol. 1, No. 3, 1964, pp. 195-200.
- M. A. Nielsen and I. L. Chuang, “Quantum Computation and Quantum Information,” Cambridge University Press, Cambridge, 2000.
- W. H. Louisell, “Quantum Statistical Properties of Radiation,” John Wiley and Sons, New York, 1973.
- R. M. Gingrich and C. Adami, “Quantum Entanglement of Moving Bodies,” Physical Review Letters, Vol. 89, No. 27, 2002, Article ID: 270402. doi:10.1103/PhysRevLett.89.270402
- P. M. Alsing, I. Fuentes-Schuller, R. B. Mann and T. E. Tessier, “Entanglement of Dirac fields in Noninertial Frames,” Physical Review A, Vol. 74, No. 3, 2006, Article ID: 032326.
- Q. y. Pan and J. l. Jing, “Degradation of Nonmaximal Entanglement of Scalar and Dirac Fields in Noninertial Frames,” Physical Review A, Vol. 77, No. 2, 2008, Article ID: 024302.
- Q. y. Pan and J. l. Jing, “Hawking Radiation, Entanglement, and Teleportation in the Background of an Asymptotically Flat Static Blcak Hole,” Physical Review D, Vol. 78, No. 6, 2008, Article ID: 065015.
- J. c. Wang, Q. y. Pan, S. b. Chen and J. l. Jing, “Entanglement of Coupled Massive Scalar Field in Background of Dilaton Black Hole,” Physics Letters B, Vol. 677, No. 3, 2009, p. 186. doi:10.1016/j.physlteb.2009.05.028
- J. c. Wang, J. f. Deng and J. l. Jing, “Classical Correlation and Quantum Discord Sharing of Dirac Fields in Noninertial Frames,” Physical Review A, Vol. 81, No. 5, 2010, Article ID: 052120. doi:10.1103/PhysRevA.81.052120
- J. c. Wang and J. l. Jing, “Quantum Decoherence in Noninertial Frames,” Physical Review A, Vol. 82, No. 3, 2010, Article ID: 032324. doi:10.1103/PhysRevA.82.032324
- S. Ghosh, G. Kar, A. Roy, A. Sen and U. Sen, “Distinguishability of Bell States,” Physical Review Letters, Vol. 87, No. 27, 2001, Article ID: 277902.
- A. Salles, F. de Melo1, M. P. Almeida1, M. Hor-Meyll, S. P. Walborn, P. H. Souto Ribeiro and L. Davidovich, “Experimental Investigation of the Dynamics of Entanglement: Sudden Death, Complementarity, and Continuous Monitoring of the Environment,” Physical Review A, Vol. 78, No. 2, 2008, Article ID: 022322.
- I. Fuentes-Schuller and R. B. Mann, “Alice Falls into a Black Hole: Entanglement in Noninertial Frames,” Physical Review Letters, Vol. 95, No. 12, 2005, Article ID: 120404.
- P. Walther and A. Zeilinger, “Experimental Realization of a Photonic Bell-State Analyzer,” Physical Review A, Vol. 72, No. 1, 2005, Article ID: 010302. doi:10.1103/PhysRevA.72.010302
- M. Dusek, “Discrimination of the Bell States of Qudits by Means of Linear Optics,” Optics Communications, Vol. 199, No. 1, 2001, pp. 161-166. doi:10.1016/S0030-4018(01)01565-6
- J. M. Raimond, M. Brune and S. Haroche, “Manipulating Quantum Entanglement with Atoms and Photons in a Cavity,” Reviews of Modern Physics, Vol. 73, No. 3, 2001, p. 565.
- H. P. Breuer and F. Petruccione, “The Theory of Open Quantum Systems,” Oxford University Press, Oxford, 2002.
- H. Carmichael, “An Open Systems Approach to Quantum Optics,” Springer, Berlin, 1993.
- W. K. Wootters, “Entanglement of Formation of an Arbitrary State of Two Qubits,” Physical Review Letters, Vol. 80, No. 10, 1998, pp. 2245-2248. doi:10.1103/PhysRevLett.80.2245
- V. Coffman, J. Kundu and W. K. Wootters, “Distributed entanglement,” Physical Review A, Vol. 61, No. 5, 2000, Article ID: 052306. doi:10.1103/PhysRevA.61.052306
NOTES
*Corresponding author.

