Received 12 February 2015; accepted 11 May 2015; published 14 May 2015

ABSTRACT

Efficient Air Conditioning (A/C) system is the key to reducing energy consumption in building operation. In order to decrease the energy consumption in an A/C system, a method to calculate the optimal tube row number of a direct expansion (DX) cooling coil for minimizing the entropy generation in the DX cooling which functioned as evaporator in the A/C system was developed. The optimal tube row numbers were determined based on the entropy generation minimization (EGM) approach. Parametric studies were conducted to demonstrate the application of the analytical calculation method. Optimal tube row number for different air mass flow rates, inlet air temperatures and sensible cooling loads were investigated. It was found that the optimal tube row number of a DX cooling coil was in the range of 5 - 9 under normal operating conditions. The optimal tube row number was less when the mass flow rate and inlet air temperature were increased. The tube row number increased when the sensible cooling load was increased. The exergy loss when using a non-optimal and optimal tube row numbers was compared to show the advantage of using the optimal tube row number. The decrease of exery loss ranged from around 24% to 70%. Therefore the new analytical method developed in this paper offers a good practice guide for the design of DX cooling coils for energy conservation.

Keywords:

Optimal Tube Row Number, Entropy Generation Minimization, Direct Expansion (DX) Cooling Coil, Building Energy Efficiency

1. Introduction

Entropy generation or irreversibility is always present in the heat and mass transfer processes taking place in heat exchangers. It degrades the thermodynamic performance of the heat exchangers, and causes the waste (destruction) of useful energy. For this reason, the minimization of entropy generation in heat exchangers has attracted considerable research interest over the last three decades.

Bejan [1] - [3] demonstrated that the irreversibility in heat exchangers stemmed from two main sources: 1) heat exchange across finite temperature differences, and 2) frictional pressure drop in fluid flow. Bejan’s work was later extended to the optimization for more realistic heat exchangers. These included the study by Vargas and Bejan [4] for the thermodynamic optimization of finned cross flow heat exchangers used for aircraft environmental control systems. The study results showed the effects of certain geometrical parameters, such as the total volume, the ratio between length and width of a heat exchanger, on entropy generation. Ogulata et al. [5] conducted an irreversibility analysis of a cross flow heat exchanger and obtained its optimum design parameters such as flow path length, heat transfer area and heat transfer volume. Lerou et al. [6] studied the optimization of a counter flow heat exchanger through minimization of entropy generation by combining the losses in heat transfer and pressure drop.

Sahiti et al. [7] tried to minimize entropy generation in a double-pipe pin fin heat exchanger. Previously validated empirical correlations were used in developing a mathematical model for optimizing the flow length and fin length of the heat exchanger. They concluded that from the thermodynamic point of view, a larger number of passages with a smaller pin height in a given frontal area were preferred for reducing the entropy generation in this kind of heat exchangers. Naphon [8] presented his theoretical and experimental results of a thermodynamic analysis for a horizontal concentric tube heat exchanger. The effects of the mass flow rates and inlet temperatures of both hot and cold working fluids on entropy generation and exergy loss in the heat exchanger were discussed based on a distributed-parameter mathematical model. Reyes et al. [9] carried out an exergy analysis which was equivalent to entropy generation analysis for a solar-assisted heat pump. A methodology for determining the condensing and evaporating temperature of the working fluid was proposed and an optimal condensing temperature was obtained. Culham and Muzychka [10] developed a novel numerical approach based on entropy generation minimization for optimizing the structure parameters of a plate fin heat sink. In addition, they considered the influence of variations of the structure parameters on the overall heat transfer coefficient of the heat sink. Saechan and Wongwise [11] investigated the optimal configuration of a plate finned tube condenser and studied the variation in the entropy generation number with a variable Reynolds number.

Although the EGM method had been widely applied in finding the optimal shape or optimal operating conditions of heat exchangers [7] - [11] , the previous reported work done to find an optimal tube row number for Direct Expansion (DX) cooling coils could not be identified in the open literature. However DX cooling coil is a key component in a DX A/C system and DX air conditioning (A/C) systems are widely used in small-medium scaled buildings. Compared with central HVAC system, they are simpler, more energy efficient and generally cost less to own and maintain.

The cooling material in the studied heat exchangers is single-phase water, while in DX cooling coil is refrigerant where both two-phase and single-phase exist and the major one is two-phase. This causes that the entropy generation calculation of DX cooling coil is more complicated compared with those of the previous heat exchangers leading to the scarcity of related research.

In an operating DX cooling coil, both sensible heat and latent heat are transferred from air to refrigerant and air pressure drops along the air flow direction. Entropy is generated during air cooling process within the DX coil, degrading the energy quality. Entropy generation in both air side and refrigerant side should be decreased or minimized so as to enhance the thermal performance of DX air cooling coils.

In the present work, optimal tube row number of a DX cooling coil will be found by using an analytical calculation method so as to optimize the shape of the DX cooling coil. Figure 1 shows an example how the shape of DX cooling coil is optimized. The triumph of analytical calculation method will be the low cost compared with trail-error experimental method.

For the purpose, an analysis of entropy generation due to the irreversibility during the air cooling process in a steadily operated DX cooling coil will be firstly carried out. Based on the analysis, a method for analytically calculating optimal tube row number of a DX cooling coil for different steady-state operating conditions will be developed and the numerical values of entropy generation are determined. This will be followed by reporting

parametric studies to illustrate the application of the analytical calculation method developed. The results of the optimal tube row number will be calculated under the variation of three key operating parameters which are inlet air mass flow rate, inlet air temperature and sensible cooling load. Finally, exergy loss when using non-optimal and optimal tube row numbers will be compared to identify the energy saving advantage by using the optimal tube row number.

2. Calculation Method

2.1. Operating Conditions of a DX Air Cooling Coil

Figure 2 shows the basic operating configuration of a DX air cooling coil commonly seen in actual installations. This is an open system with two sides: air side and refrigerant side. At the air side, hot and humid air entered into the system at a specific dry-bulb temperature (T_a,in), a specific static pressure (P_a,in) and a specific moisture content (w_a,in). After being cooled and dehumidified, the air left the system at a lower dry-bulb temperature, T_a,out, a lower static pressure, P_a,out and a lower moisture content, w_a,out. At the same time, because of dehumidification, the condensate left the system at a temperature of T_w. At the refrigerant side, there were two parts along the flow direction of refrigerant. The first part was a two-phase part where liquid refrigerant vaporizes absorbing heat from air; the second part was a superheated region where vapour refrigerant was further heated so that its temperature increased. The liquid phase refrigerant entered the cooling coil at the evaporating temperature, T_r,e, and evaporating pressure, P_r,e, and left at T_r,e + T_sh and P_r,out, where T_sh was the degree of refrigerant superheat.

2.2. Entropy Generation Minimization Exergy Analysis

To simplify the analysis the following two assumptions are made: 1) The entire cooling coil system shown in Figure 2 was enclosed in an adiabatic control volume, 2) The refrigerant pressure drops were neglected in both the two-phase and superheated regions at the refrigerant side, i.e., P_r,e = P_r,out.

The entropy generation rate in the entire control volume is:

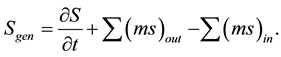(1)

At a steady state, the term is equal to zero. The difference of ∑(ms)_out − ∑(ms)_in is evaluated as follows:

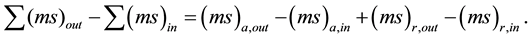(2)

At the air side, air entropy varies because of heat transfer, frictional effect and phase change [12] of water vapour in the air as follows,

(3)

The first term on the right-hand side of Equation (3) represents the irreversibility due to the heat transfer and the frictional effect on moist air stream. The last term in Equation (3) represents the irreversibility due to the condensation of water vapour. The entropy variation at the refrigerant side is

(4)

The first and second terms on the right-hand side of Equation (4) denote the irreversibility during the phase change process in the two-phase region and heating process in the superheated region, respectively. Combining Equations (1), (3) and (4), the entropy generation can be determined by:

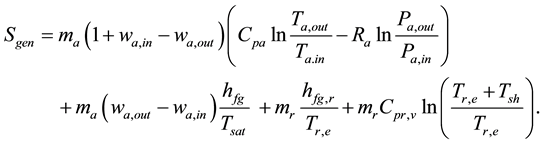(5)

Based on the fact that in practice w_a,in and w_a,out are much smaller than 1, and q_l = m_a(w_a,in − w_a,out)h_fg, q_s = m_aC_pa(T_a,in − T_a,out), Equation (5) can be rewritten as:

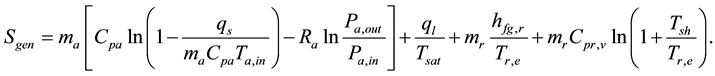(6)

The corresponding entropy generation number [1] , is defined as:

(7)

In a steady state, q_s and q_l, should be equal to the sensible and latent space cooling loads. In addition, the inlet air parameters T_a,in, P_a,in are constants when indoor air temperature setting is maintained and a supply fan speed remains unchanged. Furthermore, the saturation temperature of moist air, T_sat, is equal to the dew point temperature of inlet moist air, T_dew, which can be determined by inlet air temperature and moisture content. These parameters are independent of the thermal characteristics of the DX cooling coil. Based on these, Equation (7) is rewritten as:

(8)

where N_c denotes the entropy generation which is independent of the thermal characteristics of the DX cooling coil, to be calculated by:

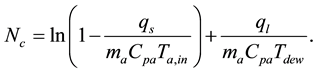(9)

Recognizing that in most A/C applications h_fg,r ~ 300C_pr,v, T_r,e < 10˚C and T_sh/T_r,e < 1 in a DX cooling coil used in a R22 DX A/C system, the second term on the right hand side is much smaller than the first term on the same side of Equation (8); therefore, Equation (8) is simplified to:

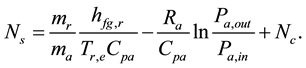(10)

Effectiveness-Ntu method is used to evaluate the thermal characteristics of the DX cooling coil. The effectiveness, ε, is

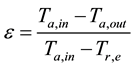(11)

hence,

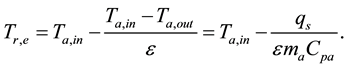(12)

For a cross-flow heat exchanger, its effectiveness ε is calculated by [13] :

(13)

For the DX cooling coil, C_min = m_aC_pa, and C_max → ∞, C_min/C_max → 0. The limit of ε as C_min/C_max approaches to zero is obtained by performing the Taylor series Expansion to Equation (13), yielding

(14)

From the definition of Ntu and Equation (14), ε could be evaluated by:

(15)

The air static pressure at the coil outlet, P_a,out, is evaluated by P_a,in − ∆P, where ∆P is given by [1] :

(16)

Combining Equations (8), (12) and (16), and recognizing that ∆P/P_a,in is considerably smaller than 1 to obtain:

(17)

The overall air side heat transfer area, A_o, and air flow length, L, are assumed to be both linearly related to the number of the tube rows, n_t. Therefore, Equation (17) becomes:

(18)

It can be seen from Equation (18), the first term increases while the second term decreases when n_t increases. There certainly exists an optimal value of n_t at which the entropy generation number, N_s, reaches minimum.

2.3. Determination the Optimal Tube Row Number

According to the previous studies [14] - [16] , it is understood that n_t has insignificant effects on both air and refrigerant side heat transfer coefficients and therefore it is assumed to be ignorable. Furthermore, we assume the overall heat transfer coefficient U_o is regarded being unrelated to n_t, and the friction factor, f, is regard being invariable with n_t according to Ref. [17] . These assumptions, even though simplify the analysis, are still useful in this pilot study.

Based on these, the optimal n_t, i.e., n_t,opt, is the root of the following equation which is obtained by partial differentiating Equation (18) with respect to n_t:

(19)

The solution of n_t,opt obtained from Equation (19) is

(20)

where α, β are defined as:

(21)

(22)

(23)

It can be seen from Equations (20)-(23), the solution of n_t,opt is determined by three types of parameter: a) DX cooling coil operating parameters such as m_a, T_a,in, q_s; b) thermal properties of air and refrigerant, such as C_pa and h_fg,r; c) and geometrical parameters such as D, c_A and c_L. The variations of any these parameters consequently cause the variation of n_t,opt.

3. Parametric Study

3.1. A Case Study

Table 1 shows one set of operating and geometric parameters used in the case study to determine corresponding n_t,opt. Using these parameters, an optimal tube row number, n_t,opt, of 6 was obtained. Figure 3 shows the variations of (N_s − N_c at different n_t (1 - 50) in. When n_t is small, the entropy generation due to air static pressure drop is low according to Equation (18). Hence, the values of (N_s − N_c) are determined by the irreversibility in heat transfer. When n_t is increased, the effectiveness, ε, of the DX coil is enhanced, leading to a decreased entropy generation in heat transfer. At the same time, however, the entropy generation due to the air static pressure drop increases linearly with the increase of n_t. At a larger n_t, entropy generation caused by air static pressure drop has dominating effect. Hence, (N_s − N_c) finally increases almost linearly with the increase of n_t.

3.2. Optimal Tube Row Number, n_t,opt in Different m_a, T_a,in and q_s

With the method developed, the investigation of the impacts of key operating parameters for a DX cooling coil on the optimal tube row number, n_t,opt, can be undertaken. In this section, the optimal tube row number under the variation of three operating parameters, i.e., m_a, T_a,in and q_s for the DX cooling coil of which the other operating and geometric parameters are shown in Table 1 were calculated.

The variation ranges for the three parameters were: m_a, 0.3 - 0.7 kg/s with interval of 0.05 kg/s; T_a,in, 20˚C - 28˚C with interval of 1˚C; q_s, 4.5 - 6.5 kW with interval of 0.25 kW, respectively. These variation ranges were selected according to common operating environment for a DX Air Conditioning system. The optimization results based on these operating conditions formed a group of optimal tube row numbers which should be adopted in common operating conditions of a DX A/C system.

As shown in Figure 4, the increase of m_a leads to a decrease in the value of n_t,opt. This is because the entropy generated during the heat transfer process decreased with an increased m_a and a smaller n_t,opt would allow the hydraulic irreversibility as shown as the second term in Equation (18) to dominates. Smaller n_t,opt means the lower air flowing resistance and therefore lower hydraulic irreversibility Figure 4 also shows the effects of variations of T_a,in and q_s on n_t,opt, respectively. It can be seen that when T_a,in increases n_t,opt decreases and when q_s increases, n_t,opt increases. These trends indicated the decreasing and increasing effects of T_a,in and q_s on the entropy generated during heat transfer and pressure drop processes. The explanation related to n_t,opt vs T_a,in is: higher T_a,in increases the temperature difference which drives the heat transfer taking place in the DX cooling coil; smaller n_t,opt decreases the heat transfer time period therefore decreases the transfer amount of useful energy in hot air to cold refrigerant, leading to a lower entropy generation. The explanation related to n_t,opt vs q_s is: larger n_t,opt can enlarge the heat transfer area when q_s increases so as to decrease the entropy generation. The difference between the variation trends of n_t,opt as T_a,in and q_s increase is for the first one, heat transfer rate can be decreased by decreasing n_t,opt even though T_a,in increases. For the second one, we can only increase n_t,opt for enhancing the heat transfer area because of the increase of q_s, the sensible heat transfer rate.

It can be seen that n_t,opt is different under different operating conditions from Figure 4. Basically, the ranges of n_t,opt shown were from 5 - 9. Previous study done by Marathe [18] indicated that the numbers of tube row number for those commonly used DX cooling coils were 3, 4, 6 and 8. In other investigations on the operating performance of DX cooling coils, the number of tube rows for the DX cooling coils were also in or close to this range. For example, Turaga et al. [19] studied the operating characteristics of DX cooling coils with their tube row numbers being in the range of 3 - 8. These previous studies suggested that optimal tube row numbers between 5 and 9 as reported in Section 3.2 are reasonable.

The results of optimal tube row numbers obtained in this paper offered a guidance for the design of a DX cooling coil The design of DX cooling coil is related to the real situations such as limitations of space and cost.

The assumptions adopted in deriving the equations cause the uncertainty of the results as well. However, the results still illustrate how to optimize the tube row number for different operating conditions, so as to enhancing the operating performance of a DX cooling coil.

4. Exergy Loss Comparison

In this section, the comparison between the exergy losses, E_xl, with the optimal tube row number and a non-op- timal one was conducted to show the advantage of the optimal tube row number. In comparison, all the other operating and geometrical conditions of the DX cooling coil were maintained as the same as shown in Table 1.

As well know, exergy loss, E_xl, is proportional to the entropy generation, or

(23)

The entropy generation number N_s can be determined using Equation (9)-(10) and Equation (18). As shown in Section 3.1, n_t,opt under conditions as shown in Table 1 is 6. However, because of the installation limit, the tube row number of commonly-used evaporator (indoor unit) of household DX Air Conditioning system is usually around 3. Here tube row number of 3 is selected to calculate the E_xl and compared with that with n_t,opt of 6. It is found that the exergy loss is around 180 W and 311 W respectively for n_t,opt of 6 and 3.

The calculation is also extend to evaluate the exery loss as the operating conditions are varied as shown in Section 3.2. All the corresponding results are shown in Figures 5-7. All of these figures show the exergy loss when using optimal tube row number is less than that when choosing the non-optimal tube row number of 3, suggesting the advantage of optimization of the tube row number of a DX cooling coil.

Saving of E_xl if using optimal tube row number is calculated,

(24)

In these figures, the relative saving of exergy loss (R_el,s) by using optimal tube row number are shown in these figures. We can see that the relative ratio ranges from 24% to 70% identifying a considerable exergy loss decrease and the merit of using optimal tube row in a DX cooling coil.

5. Conclusions

In this paper, a method for analytically calculating the optimal tube row number, n_t,opt, of a DX cooling coil is derived from entropy generation minimization principle. A method for evaluating the entropy generation due to

the irreversibility during the air cooling process in a steadily operated DX cooling coil was firstly developed. Using the method, the variation of entropy generation under the variation of tube row numbers for a DX cooling, in a case study was evaluated and the result indicated that entropy generation decreased firstly and increased secondly when the tube row number increased.

Parametric studies on the impacts of various indoor operating conditions, i.e., mass flow rate of inlet air, indoor air temperature and indoor sensible cooling load, on the optimal tube row number are undertaken. The results suggest that the optimal tube row number lies between 5 and 9 when the indoor operating conditions vary with their suitable ranges and under a set of specified operating conditions for a given DX cooling coil having a fixed geometry.

Result of row number which ranges from 5 to 9 is considered reasonable because it is commonly seen in previous relative literatures. The results also show that increase of m_a leads to a decrease of n_t,opt; increase of T_a,in to an decrease of n_t,opt and increase of q_s to an increase of n_t,opt. The saving of exergy loss due to the application of the optimal tube row number in DX cooling coil has been calculated and reported, illustrating a significant energy saving from 24% - 70% as the operating conditions varies.

The analytical method proposed in this paper can be applied conveniently for calculating optimal tube row number of a DX cooling coil. Even though assumptions are adopted in the development of analytical method, the results from the analytical method are still consistent to ones in previous researches. Energy saving effect of the optimal tube row number reported illustrates its advantage and potential in real application.

Acknowledgements

We gratefully acknowledge the financial supports from the Small Research Grant (UNNC), Ningbo Natural Science Foundation (2014A610025) and (2014A610172), and Qianjiang Talent Scheme (QJD1402009).

References

Nomenclatures

A_o overall heat transfer area on the air side of a DX cooling coil, m²

C_p specific heat, J/(kg∙K)

c_A a linear factor between the overall heat transfer area and the tube row number, m²

c_L a linear factor between air flow length and the tube row number, m

D air side hydraulic diameter of a DX cooling coil, m

E_xl exergyloss, W

E_xl,s saving of exergy loss, W

f friction factor

G mass velocity, kg/(m²/s)

h_fg latent heat of vapourization of water, J/kg

h_fg,r latent heat of vapourization of liquid refrigerant, J/kg

L air flow length in a DX cooling coil, m

m mass flow rate, kg/s

N_s total entropy generation number

N_c entropy generation number defined by Equation (9)

Ntu number of heat transfer unit

n_t tube row number

P pressure, Pa

∆P pressure difference, Pa

q_l latent cooling load of a DX cooling coil, W

q_s sensible cooling load of a DX cooling coil, W

R_a ideal gas constant, J/(kg∙K)

S entropy, W/K

S_gen entropy generation, W/K

s specific entropy, W/(kgK)

T temperature, ˚C

T_dew dew point temperature, ˚C

T_sat saturation temperature of moist air, ˚C

T_sh degree of superheat, ˚C

T_w temperature of condensate, ˚C

T_∞ environment temperature, K

t time, s

U_o overall air side heat transfer coefficient of a DX cooling coil, W/(m²∙K)

w moisture content, kg/kg

Greek Letters

α parameter defined by Equation (21-1)

β parameter defined by Equation (21-2)

ε effectiveness of a DX cooling coil

ρ density, kg/m³

Subscripts

a air

dl dimensionless

e evapourating

in inlet to the cooling coil

opt optimum

out outlet of the cooling coil

r refrigerant

v vapour

Acronyms

DX direct expansion

NOTES

^*Corresponding author.