Open Journal of Statistics
Vol.06 No.01(2016), Article ID:63351,7 pages
10.4236/ojs.2016.61002
Comparison of Cost Incurred in Two Survey Methodologies for Measles Vaccine Coverage
Dilip C. Nath, Bhushita Patowari
Department of Statistics, Gauhati University, Guwahati, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 December 2015; accepted 2 February 2016; published 5 February 2016
ABSTRACT
Background: The World Health Organization (WHO) initiated the Expanded Program on Immunization (EPI) in 1974. It has been widely used in different studies. Along with this, other survey methodologies have been compared to study immunization coverage at different regions. To consider different survey methodologies, one of the most important factors is the cost incurred that survey methodology. A survey method is considered as more efficient or better than the other survey method if the cost incurred in a particular method is less than the other one. Methods: In this study, cost incurred in two stage (30 × 30) cluster sampling and systematic sampling methods have been compared using a cost function for measles vaccine coverage. Measles vaccine coverage data has been taken from the survey “Comparison of Two Survey Methodologies to Estimates Total Vaccination Coverage” sponsored by Indian Council of Medical Research (ICMR), New Delhi. Results: The results show that there are no significant differences between the point estimates of measles vaccine coverage under the considered survey methodologies. But the cost incurred in systematic sampling is more than that of two stage cluster sampling. Conclusion: It can be concluded that systematic sampling survey is costlier than that of two stage cluster sampling for this study population.
Keywords:
Two Stage Cluster Sampling, Systematic Sampling, Immunization Coverage

1. Introduction
The World Health Organization (WHO) initiated the Expanded Program on Immunization (EPI) in May 1974 with the objective to vaccinate children throughout the world. Since then it has been widely used to access the immunization coverage. India launched National Immunization Programme called Expanded Programme of Im- munization (EPI) in 1978 with the introduction BCG, OPV, DPT and typhoid-paratyphoid vaccines. Typhoid- paratyphoid vaccine was dropped from EPI in 1981, reportedly due to considered higher reactogenecity and low efficacy of the vaccines and also due to perceived reduced burden of typhoid disease in the country. The EPI was rechristened with some major change in focus by the launch of Universal Immunization Programme (UIP) on November 19, 1985. The measles vaccine was added to the existing schedule [1] . Along with EPI cluster sampling, different sampling methodologies have been used to study the vaccination coverage. They are commonly lot quality assurance sampling (LQAS), systematic sampling, stratified sampling and simple random sampling (SRS). Yoon et al. (1997) mentioned that a method that eliminated many of the logistical problems of SRS was cluster sampling. The primary sampling units are clusters, often defined so as to be convenient for the researcher. Typically, EPI cluster surveys have consisted of 30 clusters of 7 children each (for immunization coverage surveys). However, the method has been modified and adapted for estimation of different health parameters say 30 clusters of 14 children, 30 clusters of 30 children, 30 clusters of 68 children and sometimes 19 clusters or 45 clusters also. They study the cost of conducting EPI cluster sampling in assessing the prevalence of diarrhea and dysentery compared with stratified random sampling [2] . Rose et al. (2006) compared the results of two stage (30 × 30) cluster and systematic sampling to measure retrospective mortality. The results show that the traditional two stage cluster survey designs can give similar results to the systematic survey design when making rapid estimates of retrospective mortality in a setting where the mortality point estimate is not above the emergency threshold [3] . In a study, Megiddo et al. (2014) evaluated the health and financial effects of interven- tions introducing a rotavirus vaccine to the immunization program. Immunization is one of the most cost-effec- tive interventions for improving health outcomes [4] .
Different survey methodologies have different merits and some of demerits are also compared to each other. In general, a survey methodology will be considered better than the other one if the considered methodology gives better estimates than the later one. But at the same time, cost incurred and time is required to complete that survey is also important. Singh et al. (1996) evaluated immunization coverage in a primary health centre (PHC) area with lot quality assurance sampling (LQAS) and EPI surveys using paramedical personnel as field staff. The time required and the expenses incurred in the two surveys have been discussed. The estimated costs of the surveys are a ratio of 1:1.6 for the cluster survey and LQAS survey respectively [5] .
In this study, a cost function has been proposed under both two stage (30 × 30) cluster and systematic sampling and that has been compared by taking the coverage for measles vaccine in the capital city of Assam, India.
2. Methodology
For illustration, the data from a recent survey has been collected by using two stage (30 × 30) cluster and systematic random sampling which has been performed under the project “Comparison of Two Survey Methodologies to Estimate Total Vaccination Coverage” sponsored by Indian Council of Medical Research (ICMR), New Delhi and carried out in Guwahati, the capital city of Assam. In this survey, coverage of BCG, OPV, DPT, Hepatitis B, Hib, Measles, MMR vaccine has been taken. The sample size is altogether 1800 (900 in each sampling). Here only measles vaccination coverage has been considered. The detail survey methodologies have been discussed in earlier study [6] .
Two stage cluster sampling is a survey sampling method where data have been collected in two stages. In the first stage clusters are selected and in the second stage sampling units are selected from already selected clusters. The clusters may be any geographical region which is well defined. In the first stage 30 clusters have been selected and from that selected clusters 30 sampling units have been collected. This method has advantages from simple random sampling that it does not require the whole list of sample space. Also it takes less time to complete survey area which in turn reduces the cost of the survey method. This methodology is also easy for the surveyor to conduct survey. Systematic sampling is a random sampling in which the first unit is selected according to some predesigned pattern and the rest are selected automatically. Here first unit is selected from the random number table and thereafter each sampling unit is selected at an interval of 10 units until it completed 30 units.
3. Determination of Cost Function
Let us denote:
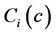 = cost per household covered in two stage cluster sampling
= cost per household covered in two stage cluster sampling
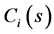 = cost per household covered in systematic random sampling
= cost per household covered in systematic random sampling
Also denote:
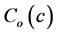 = fixed cost in two stagecluster sampling
= fixed cost in two stagecluster sampling
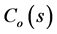 = fixed cost in systematic random sampling
= fixed cost in systematic random sampling
where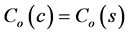 .
.
Then we have,
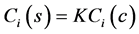 where K can take values <1, >1 or =1
where K can take values <1, >1 or =1
Depending on the value of K the cost incurred in systematic sampling will be less than, more than and equal to cluster sampling according to K < 1, K > 1 and K = 1 respectively.
Now for two stage (30 × 30) cluster sampling scheme, n = 900 units, we have
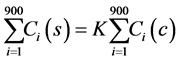
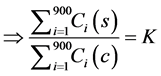 (1)
(1)
Now, if K = 1, we have from (1)
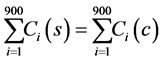 (2)
(2)
That is cost incurred in both the sampling method are equal.
If K < 1, we have
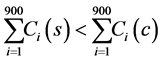 (3)
(3)
It implies that cost incurred in systematic random sampling is less than the two stage (30 × 30) cluster sampling.
Again, if K > 1 then we have
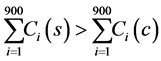 (4)
(4)
This implies that systematic random sampling is more costly than two stage (30 × 30) cluster sampling.
It is observed (Table 1) that on an average 148 household have to visit to complete 30 eligible children in a ward under two stage (30 × 30) cluster sampling whereas it is 459 household under systematic sampling. That is to complete the survey in a ward number of household visited in systematic sampling is almost three times than that of the two stage (30 × 30) cluster sampling.
As more number of household to be visited under systematic sampling, the time required to complete the survey in a particular ward will almost three times more than two stage (30 × 30) cluster sampling. That is surveyors have to cover more distance, spent more money and total man-days required for the survey. Hence cost incurred is automatically higher in systematic random sampling than that of the two stage (30 × 30) cluster sampling.
So, we can assume that K = 3 which is greater than 1, from Equation (4), we have
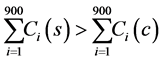 (5)
(5)
Adding fixed cost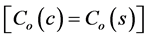 , on both sides of (5), we have
, on both sides of (5), we have
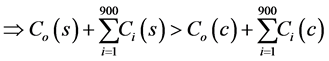
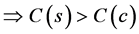 (6)
(6)
Þ total cost in systematic random sampling > total cost in two stage (30 × 30) cluster sampling.
Table 1. Household covered in each ward under two stage (30 × 30) cluster and systematic sampling schemes.
Thus we have,
4. Analysis
For this study we consider the measles vaccination coverage. Measles vaccine coverage has been estimated under two stage (30 × 30) cluster and systematic sampling for each ward where the proportion of children vaccinated against measles vaccine is denoted by

H0:
Against the alternative,
H1:
The test statistic (for difference of proportion) is given by
where 

The confidence interval for the difference between two population proportions is constructed round

The confidence interval is then given by
where 
5. Results and Discussion
From Table 2 of estimated proportion of measles vaccine with Z-statistic and confidence intervals it has been observed that the z-statistics are insignificant except for the ward number 5. Thus the null hypothesis may be accepted and it can be concluded that there are no significant differences between the estimated proportions under two stage (30 × 30) cluster and systematic random sampling. But considering the factor time and cost as discussed in the previous section (Determination of cost function), systematic sampling is more time consuming and hence cost incurred is more than that of two stage (30 × 30) cluster sampling.
Yadav et al. (2009) assessed the impact of the pulse polio immunization programme at the primary health level in terms of services, time and cost. The study found that a single round of intensified pulse polio immunization consumes a substantial number of person-hours and leads to a temporary suspension of routine services provided at the primary health centre [8] . Casta˜neda-Orjuela et al. (2013) mentioned that the cost of Expanded Programs on Immunization (EPI) is an important aspect of the economic and financial analysis needed for planning purposes. Costs also are needed for cost-effectiveness analysis of introducing new vaccines. They described a costing tool that improves the speed, accuracy, and availability of EPI costs and that was piloted in Colombia. The analysis shows that personnel, cold chain, and transportation are important components of EPI and should be carefully estimated in the cost analysis, particularly when evaluating new vaccine introduction [9] . An economic analysis was performed (Chen et al., 2011) to estimate the cost of trachoma prevalence surveys conducted between 2006 and 2010 from 8 national trachoma control programs in Africa. In that study, they presented an analysis of costs incurred in the implementation of trachoma prevalence surveys across eight national trachoma control programs [10] . Macintyre (1999) studied the trade-offs in cost and quality of information obtained from a rapid assessment survey in Ecuador. The results from the rapid survey were compared with results obtained from a national survey conducted six months earlier. The objective was to see what alternative policies might be arrived at if the data from the rapid survey were used in place of the large survey. In addition, the relative costs of obtaining that information were measured. The rapid survey was three times as cost-efficient as the traditional survey, if relative bias is not taken into account [11] . Lwanga and Abiprojo (1987) studied the differ-
Table 2. Estimated proportion of measles vaccine with Z-statistic and confidence intervals (CI).
*Significant at 5% probability level.
ences in survey time and cost for a rural and an urban setting of Indonesia between the standard EPI survey method and the statistically rigorous approach where majority of the children are not vaccinated according to the national immunization schedule. The estimates obtained with SRS surveys were more precise than those with EPI surveys, but they were more costly. The relatively higher precisions of the estimates do not justify the indiscriminate use of the SRS method [12] . In this study estimated measles vaccine coverages have not shown any significant difference between the two survey methodologies viz two stage (30 × 30) cluster and systematic sampling but the cost incurred in systematic sampling is higher than that of two stage (30 × 30) cluster sampling.
6. Concluding Remarks
From the study, it can be concluded that only good estimates of parameters under a sampling strategy are not sufficient to say that a particular methodology is to be adopted. Together with that time and cost incurred in survey methodology is also very important to say that a particular sampling methodology is better than the other one. In this study, it has been observed that there is significant difference between the estimates of measles vaccine coverage in the considered region of Assam, but the cost incurred in systematic random sampling is more than that of the two stage (30 × 30) cluster samplings.
Acknowledgements
This work is financially supported by Indian Council of Medical Research (ICMR), New Delhi (grant number 69/40/2008-ECD-II) and UGC-BSR one time grant (No. F. 19-145/2015(BSR)) and provided to the first author.
Conflict of Interest
None.
Cite this paper
Dilip C.Nath,BhushitaPatowari, (2016) Comparison of Cost Incurred in Two Survey Methodologies for Measles Vaccine Coverage. Open Journal of Statistics,06,7-13. doi: 10.4236/ojs.2016.61002
References
- 1. Lahariya, C. (2014) A Brief History of Vaccines & Vaccination in India. Indian Journal of Medical Research, 139, 491-511.
- 2. Yoon, S.S., Katz, J., Brendel, K. and West Jr., K.P. (1997) Efficiency of EPI Cluster Sampling for Assessing Diarrhea and Dysentery Prevalence. Bulletin of the World Health Organization, 75, 417-426.
- 3. Rose, A.M.C., Grais, R.F., Coulombier, D. and Ritter, H. (2006) A Comparison of Cluster and Systematic Sampling Methods for Measuring Crude Mortality. Bulletin of the World Health Organization, 84,290-296.
http://dx.doi.org/10.2471/BLT.05.029181 - 4. Megiddo, I., Colson, A.R., Nandi, A., Chattarjee, S., Prinja, S., Khera, A. and Laxminarayan, R. (2014) Analysis of the Universal Immunization Programme and Introduction of a Rotavirus Vaccine in India with India Sim. Vaccine, 32, A151-A161.
http://dx.doi.org/10.1016/j.vaccine.2014.04.080 - 5. Singh, J., Jain, D.C., Sharma, R.S. and Verghese, T. (1996) Evaluation of Immunization Coverage by Lot Quality Assurance Sampling Compared with 30-Cluster Sampling in a Primary Health Centre in India. Bulletin of the World Health Organization, 74, 269-274.
- 6. Nath, D.C. and Patowari, B. (2014) Estimation and Comparison of Immunization Coverage under Different Sampling Methods for Health Surveys. International Journal of Population Research, 2014, Article ID: 850479.
http://dx.doi.org/10.1155/2014/850479 - 7. Gardner, M.J. and Altman, D.G. (1986) Confidence Intervals rather than P Values: Estimation rather than Hypothesis Testing. British Medical Journal, 292, 746-750.
http://dx.doi.org/10.1136/bmj.292.6522.746 - 8. Yadav, K., Rai, S.K., Vidushi, A. and Pandav, C.S. (2009) Intensified Pulse Polio Immunization: Time Spent and Cost Incurred at a Primary Health Centre. The National Medical Journal of India, 22, 13-17.
- 9. Casta~neda-Orjuela, C., et al. (2013) Using Standardized Tools to Improve Immunization Costing Data for Program Planning: The Cost of the Colombian Expanded Program on Immunization. Vaccine, in press.
- 10. Chen, C., Cromwell, E.A., King, J.D., Mosher, A., Harding-Esch, E.M., et al. (2011) Incremental Cost of Conducting Population-Based Prevalence Surveys for a Neglected Tropical Disease: The Example of Trachoma in 8 National Programs. PLoS Neglected Tropical Diseases, 5, e979.
http://dx.doi.org/10.1371/journal.pntd.0000979 - 11. Macintyre, K. (1999) Rapid Assessment and Sample Surveys: Trade-Offs in Precision and Cost. Health Policy and Planning, 14, 363-373.
http://dx.doi.org/10.1093/heapol/14.4.363 - 12. Lwanga, S.K. and Abiprojo, N. (1987) Immunization Coverage Survey: Methodological Studies in Indonesia. Bulletin of the World Health Organization, 65, 847-853.










