Received 14 October 2014; revised 5 November 2014; accepted 15 November 2014

ABSTRACT

Clustering Lasso, a new regularization method for linear regressions is proposed in the paper. The Clustering Lasso can select variable while keeping the correlation structures among variables. In addition, Clustering Lasso encourages selection of clusters of variables, so that variables having the same mechanism of predicting the response variable will be selected together in the regression model. A real microarray data example and simulation studies show that Clustering Lasso outperforms Lasso in terms of prediction performance, particularly when there is collinearity among variables and/or when the number of predictors is larger than the number of observations. The Clustering Lasso paths can be obtained using any established algorithm for Lasso solution. An algorithm is proposed to construct variable correlation structures and to compute Clustering Lasso paths efficiently.

Keywords:

Clustered Variables, Lasso, Principal Component Analysis

1. Introduction

We are often interested in finding important variables that are significantly related to the response variable and can be used to predict quantities of interest in regressions and classification problems. Important variables are often shown in clusters where variables in the same cluster are highly correlated and have similar pattern relating to the response variable. For example, a major application of microarray technology is to discover important genes and pathways that are related to clinical outcomes such as the diagnosis of a certain cancer. Typically, only a small proportion of genes from a huge bank have significant influence on the clinical outcome of interest. In addition, expression data frequently have cluster structures: the genes within a cluster often share the same pathway and are therefore similarly related to the outcome. When regression is adapted in this setting, we often face the challenge from multi-collinearity of covariates. An ideal variable selection procedure should be able to find all genes of important clusters rather than just some representative genes from the clusters. Typically, two characteristics, pointed out by [1] , evaluate the quality of a fitted model: accuracy of prediction on new data and interpretation of the model. For the latter, the sparse model with fewer selected covariates is preferred for interpretation due to its simplicity. However, when multiple variables share the same mechanism for explaining the response, all the involved variables should have an equal chance of being selected, and should exhibit the same relationship to the outcome in the fitted model, for scientific reasoning.

It is well known that the ordinary least square estimate (OLS) in linear regression often performs poorly when some of the predictors are highly correlated. OLS would generate unstable results where the estimates have inflated variances. Regularizations have been proposed to improve OLS. For example, ridge regression [2] penalizes the model complexity by the 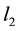penalty of the coefficients. This method was proposed to solve the collinearity problem by adding a constant to the diagonal terms of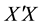, where 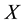is the observation or design matrix. Ridge regression stabilizes the estimates through the bias-variance trade-off. It can often improve the predictions but cannot select variables. [3] proposed the Lasso method by imposing an 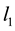-penalty on the regre- ssion coefficients. Lasso is a promising method, as it can improve prediction and produce sparse models simultaneously. However, when high correlations among predictors are present, the predictive performance of Lasso is dominated by ridge regression [3] . Moreover, when there is a cluster of variables, in which each variable associates with the response variable similarly, Lasso tends to arbitrarily select one variable from the cluster instead of identifying the cluster [1] ; see also Section 2 for more discussion. Elastic Net, proposed by [1] , combines both 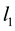and 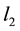penalties of the coefficients as the regularization criterion. The method is promising in that it encourages cluster effects and shows improved predictive performance over Lasso. Elastic Net can automatically choose cluster variables and estimate parameters at the same time. Many other methods can be used to choose clustered variables, such as principal component analysis (PCA). [4] defined “eigen-arrays” and “eigen-genes” in this way. But PCA can not choose sparse models. [5] proposed sparse principal component analysis (SPCR), which formulated PCA as a regression-type optimization problem, and then obtained sparse loadings by imposing the Elastic Net constraint. SPCR can successfully yield exact zero loadings in principal components. However, for each principal component, a regularization parameter has to be selected, which results in an overwhelming computational burden when the number of parameters is large. Other penalized regression methods have been proposed for group effect [6] - [13] . However, these methods either pre-suppose a grouping structure or assume that each predictor in a group shares an identical regression coefficient.

In practice, we often have some prior knowledge about the structure of variables and would like to make use of a priori information in analysis. For example, in gene analysis, we know the pathways and genes involved in these pathways. Therefore, we would like to group the involved variables in the same pathway together. Another example is in spatial analysis, we would like to keep a certain correlation structure among the spatial error terms. For example, sometimes we would like to fit a different coefficient for a certain variable at different regions (e.g., if the variable has different effect at different regions) but keep a correlation structure among the coefficients at neighborhood regions. The conditional autoregressive model (CAR, [14] ) is one of the methods that can be used to keep such correlation structure.

In this paper, we propose a method that encourages cluster variables to be selected together and can incorporate available prior information on coefficient structures in variable selection. When there is no prior information on coefficient structure, we propose a data augmentation algorithm to find the structure. Moreover, the method uses the Lasso regularization to choose sparse models. The proposed method can be solved by any efficient Lasso algorithm such as least angle regression (LARS, [15] ) and the coordinate-wise descent algorithm (CDA, [16] ). We call our method the Clustering Lasso (CL).

The rest of the paper is organized as follows. In Section 2, we review the Lasso method and discuss its limitation in identifying clustered variables. Then we propose the Clustering Lasso in a Bayesian setting. Its counterparts in the Frequentist setting and computational strategies are discussed in Section 3. Sections 4 and 5 demonstrate the predictive and explanatory performance of CL through real examples and simulations. Finally, conclusions and future work are discussed in Section 6.

2. Clustering Lasso in Bayesian Setting

Consider linear regression settings with the response vector 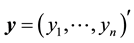and 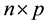dimensional input matrix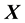. The 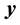and columns of 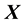are centered and standardized to have the same 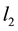norm. The Lasso estimates 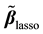are calculated by minimizing

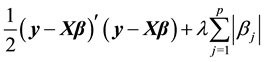(1)

The solution of Lasso can be obtained through LARS or CDA. Compared with ordinary linear regressions, Lasso shows superior predictive performance and more stable estimates. Moreover, Lasso can often select variables and estimate coefficients simultaneously.

Group effect has been defined by [1] in the linear regression setting. Let 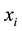be the 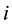th predictor. The estimates of coefficients have the group effect if would result in the estimated coefficients. [1] further proved that if the solution for estimation is to minimize the objective function of the form:

(2)

and the penalty term, , is strictly convex, then the estimates from Equation (2) enjoy the group effect property. In Lasso, is norm of, which is not strictly convex. Zou and Hastie proved that in this case Lasso estimates do not have the group effect. This is also understandable through the Lasso solution path from LARS . In LARS , suppose a variable is selected in the model. Its coefficient solution path will move in a direction to reduce the correlation between and the current residual, , until another variable, say, has the same correlation to the current residual as does. At this point, variable is added into the model. If is highly correlated with, when the correlation between and the residual decreases, so does that between and the residual. Therefore, if has been included in the model, Lasso is less likely to select the highly correlated variable in the model. Consequently, Lasso cannot select clustered variables.

In a Bayesian setting, if is the ith row of, [3] showed that the Lasso solution is identical to the posterior mode of the coefficients when the prior distributions of the coefficients are set as independent double exponential distributions, where

In Lasso, the penalty term of model complexity is. Because each coefficient is penalized equally, each one can be shrunk to zero independently. When the variables are clustered, an ideal solution path should be that the clustered variables are selected together. Therefore, we would like to penalize the coefficients with a restriction that keeps the correlation structure among the variables. With the penalization, if the coefficient of one variable is nonzero, those variables in the same cluster are less likely to be zero. For this purpose, we assume a correlation structure, specified as the structural correlation matrix, of the coefficients.

For simplicity, assume that the variance of the random error, , and the structural correlation matrix are known. Then the likelihood and prior distributions can be set as:

Therefore, the posterior distribution of has the form

(3)

with a vector,. The posterior mode of in the distribution (3) is the solution to

(4)

Relating Equation (4) to the Bayesian Lasso solution to (1), we naturally infer the Clustering Lasso in Frequentist setting.

3. Clustering Lasso

3.1. Clustering Lasso and Its Grouping Effect

In Frequentist setting, we modify the penalization function in Lasso to retain a presumed correlation structure among coefficients. Let and be the jth element of. The Clustering Lasso estimate is defined as the solution to

(5)

where is the regularization parameter. Note that instead of restricting, we restrict. Therefore,’s are not penalized independently and clustered variables could be chosen. Let, with dimension, be the jth row of and let, a matrix. The penalty term used in expression (5) can also be written as, which is intermediate between the penalty and the

penalty. When is an identity matrix, the Clustering Lasso is identical to the ordinary Lasso method. Otherwise, the penalty function is strictly convex. Using Lemma 2 developed by [1] , the solution to Expression (5) has the group effect. Therefore, Clustering Lasso can select variables by clusters.

Figure 1 illustrates the Clustering Lasso penalty contours with two predictors. The right figure shows the penalty contour when the two predictors are correlated and the left one shows the contour when the two predictors are independent, which is identical to the Lasso method. The sums of the squared errors have elliptical contours, centered and minimized at the full least squares estimate. The constraint region of Lasso is the diamond region, while that for the Clustering Lasso is the parallelogram region defined by

. The optimal estimates are realized at the place where the elliptical contours first hit the

constraint regions. The sides of the parallelogram are decided by the structural correlation matrix.

3.2. Computation

The Clustering Lasso is an extension of the Lasso method. Let. So the solution to Expression (5) is, where is

(6)

Therefore, all the established algorithms for Lasso solution, such as the least angle regression (LARS, [15] ), could be used for Clustering Lasso.

3.3. The Clustering Lasso Algorithm

We can incorporate prior knowledge of clustering into a structural correlation matrix. For example, Kyoto Encyclopedia and Genes and Genomes (KEGG) and many other biological databases can be referred to in gene analysis to construct the structural correlation matrix. It is required that the structural correlation matrix be symmetric. When no prior information is readily adaptable, a natural method is to use the modified correlation matrix of the observed data, meaning that the coefficients should have a correlation structure that is similar to how the covariates are correlated. There are several well-established potential choices such as partial correlation matrix [17] . In this paper, we propose to use a modified correlation matrix so that if two variables and are not significantly correlated, , the ith row and jth column element of, is set to be zero. As the solution

for is, zero elements in are desired so that when s are shrunk to zero, which is possible

by the Lasso property, some s could also be shrunk to exact zero.

In detail, we develop Algorithm 1―the Clustering Lasso algorithm. Let, , and, in be three prespecified numbers, and be a matrix.

Algorithm 1 Clustering Lasso

1. For

for

do correlation test between and, let

2. Do eigen decomposition on so that and let if for .

3. Let and.

4. Do Lasso on and get the coefficient solution.

5. is the solution to Clustering Lasso.

Note that only when some elements of are set to be zero, could s be shrunk to exact zero when’s are shrunk to zero by Lasso. A special case is when is a block diagonal matrix. To choose sparse models, we need to identify clusters of covariates, where variables in the same cluster are assumed to be correlated while those from different clusters are independent. For this purpose, there are two shrinkage steps in Algorithm 1. Step (1) shrinks the correlation coefficients to zero if there is no significant correlation between the pair of covariates at the significance level or if the magnitude of correlation is smaller than a pre-set value. When two covariates are not correlated, there is little chance that the two variables relate to the response variable with the same underlying pathway. Therefore, the coefficients of the two variables can be estimated independently. Step (2) shrinks some eigen-values of to zero if the corresponding eigenvector explains less than times the total variance of. The two shrinkage steps cannot guarantee that some elements of be zero. Subjective intervention can help for this purpose. One resolution is to cluster the covariates first and then calculate the correlation matrices for each cluster, which in turn used to build the diagonal blocks of. In addition to building a diagonal block matrix, another resolution is to adapt shrinkage methods in the eigen decomposition process of, so that some loadings of the eigenvectors might degenerate to 0. ScotLASS [18] and sparse principal component analysis (Zou et al., 2006) can serve this purpose. However, these methods require extra computations for each principal component, which brings in high computational costs. The nonzero elements of the jth row of imply that the corresponding covariates belong to the jth cluster. Ideally, their values should be proportional to the contributions of each covariate to the cluster in explaining the outcome. As pointed out by a referee of the paper, clusters in the proposed method are identified by rows of, where is defined as with being the diagonal matrix of eigenvalues and columns of eigen- vectors of. As in principal component analysis, the nonzero elements of are difficult to interpret in practice. The referee recommends setting the elements of to be 0 or 1 based on the absence or presence of non-zero elements, respectively. In the paper, we set the estimate of to be zero, if its estimated value is very close to zero, i.e. if.

3.4. Choice of Tuning Parameters

Four parameters, , are to be chosen for Algorithm 1. is the significance level used to decide whether the correlations between a pair of covariates should be considered to restrict the estimation of their coefficients. We usually select the significance level at 0.05, the traditional significance level. When the data set is large, we can reduce the significance level. Since the correlation would be always significant when little correlation exists and the number of observations is large, we set another restriction on the magnitude of correlation-, above which we would like to use the correlation as a restriction to the coefficient parameters. is chosen subjectively by researchers. Algorithm 1 Step (2) is similar to the principal component analysis except that the eigen decomposition is based on the correlation matrix modified by Step (1). specifies the minimum proportion of variance explained by the eigen vector, below that, the eigen vector will not be used for further analysis. is set at a small value, typically, where is the total number of covariates.

The last parameter to be tuned is. In Lasso, the conventional tuning parameter is the fraction of the -norm. There are well-established methods for choosing. Tenfold cross-validation (CV) on training data is the method we used in this paper. The training dataset is divided into ten folds randomly. One fold of the data is used as validation data, on which the prediction error is calculated based on the model fitted from the other nine folds of data. is tested on a fine grid on. It takes the value that minimizes the averaged prediction error from CV. We can also use ten-fold CV to tune and. We found that only a few representative values for

need to be cross validated to obtain good results, which are.

4. Microarray Data Example

We used the proposed method on an Affymetrix gene expression dataset. The data were collected by Singh et al. [19] and consists of 12,600 genes, from 52 prostate cancer tumor samples and 50 normal prostate tissue samples. The goal is to construct a diagnostic rule based on the 12,600 gene expressions to predict the occurrence of prostate cancer. Support vector machine (SVM, [20] ), Ridge, Lasso, Elastic Net, Weighted Fusion (w.fusion) and Clustering Lasso were all applied to this dataset. We tried four types of Clustering Lasso methods:

1. CL1:, , and;

2. CL2:, , and;

3. CL3:, , and;

4. CL4:, , and.

To apply these methods, we first coded the presence of prostate cancer as a 0-1 (no and yes) response. The classification function is (fitted value), where is the indicator function. For comparison, we randomly select 52 samples as training data, based on which the diagnostic rules are constructed, and the rules are in turn tested on the remaining 50 samples.

The dataset was split 20 times. For each repetition, a 1000-gene set was preselected based on the training data to make the computation manageable. The genes are those “most significantly” related to the response, tested by individual t-statistics. Figure 2 shows the boxplots of the misclassification rates on the test data sets from different classifiers. The misclassification rates are summarized in Table 1. Overall, the misclassification rate from Clustering Lasso is competitive with Elastic Net and Ridge, and is better than Lasso, Weighted Fusion, and SVM. For the computational time, Clustering Lasso is comparable to the Lasso method and is much more efficient than Elastic Net and Weighted Fusion. Within the four Clustering Lasso methods, the ones with more restrictions on eigenvalues and the magnitudes of correlations perform a little bit worse.

Table 2 shows the average number of genes selected from the 20 repetitions based on different methods. The analyses were based on 1000 genes and 52 observations. We see that Lasso selected fewer than 52 genes. Elastic Net eliminated few genes―the average number of selected genes was close to 1000. Cluster Lasso identified about 25% genes as important. However, we do not know whether the chosen genes are, in fact, important or not. The efficiency of variable selection is further assessed by simulation studies.

5. Simulation Studies

We applied Clustering Lasso on some simulations to test its prediction accuracy in regressions when compared with Ridge, Lasso, Elastic Net, and Weighted Fusion. The first three simulations are adapted from the Elastic Net paper [1] . To begin, datasets are simulated from the true model:

For each scenario, we simulated 100 data sets, each consisting of a training data set and an independent test data set. Here are the details of the four scenarios.

1. In example one, we simulated observations as training data and 200 observations as test data. We let and. The pairwise correlation between and

was set to be.

2. In Example two, we simulated 200 training data and 400 testing data. There are 40 predictors such that

3. Example 3 has the group setting that and, where the predictors are gene- rated as

As explained by [1] , three groups are equally important groups, and each group contains five covariates. We created observations as training data and 400 as testing data.

The fourth simulation is a modification of the third example to emphasize the group effects. The true model has the form where. The predictors we observed are

The latent variables, and, directly relate to the response variable, where is more important than. A nuisance variable, does not related to. relate to at different levels. In terms of gene analysis, we can think of, and as underlying pathways, some of which are related to the disease measured by. We observed the gene expression levels, , and would like to identify the related pathways.

We used all four Clustering Lasso methods. In all examples, the results from the four Clustering Lasso methods are close to each other. The prediction results from Lasso, CL2, CL4, Elastic Net, Ridge, and Weighted Fusion are summarized in Table 3 and Figure 3. In Figure 3, relative MSE was defined as the MSE of the corresponding method divided by the minimum MSEs from all the methods. We see that Clustering Lasso always performs better than the Lasso method, and it is close to or better than Ridge, Weighted Fusion and Elastic Nets, even under collinearity and group effect situations.

Table 4 shows the results of variable selection. The two numbers in each cell are the proportion of times an important factor is chosen and the proportion of times a false factor is chosen, respectively. We see that compared with Elastic Net, Weighted Fusion and Lasso, Clustering Lasso is superior at selecting important factors. However, like Weighted Fusion, it is more likely to over select variables than Elastic Net. In Example 2,

since all variables are highly correlated, Clustering Lasso cannot identify the most important variables. In comparison, Clustering Lasso performs very well in Examples 3 and 4, when clusters of variables play an important role in real model.

Finally, to show how Clustering Lasso chooses covariates in groups and the behavior of the coefficients for the selected variables, we illustrate the differences between Lasso and Clustering Lasso by a modified example from [1] . Let, and be three independent variables with the uniform distribution. The

response variable is generated as. With the random error terms, the nine

observed predictors are

The variables, and are from group 1, with the direct effect., and are from group 2, with the direct effect. The effect from on is much smaller than from―the coefficient for is 1 compared with 0.2 for. Variables, and are from, which does not relate to the response variable. The within-group correlations are almost 1, while the between group correlations are almost 0. Figure 4 shows the solution paths for Lasso, Elastic Net and CL2.

We also use this simulation to compare the sensitivity and specificity of the listed methods in finding significant covariates. The simulation is repeated 100 times. Table 5 summarizes the number of times that the coefficients of are not zero. We find that the proposed Clustering Lasso of all versions can uniformly identify the important covariates while is less likely to select non-significant covariates than Lasso, Elastic Net and Weighted Fusion.

6. Conclusions and Future Works

We find that the Clustering Lasso, is a novel predictive model that produces sparse model with good predictive performance, while encouraging group effects. The empirical results from a two-class microarray data classifica- tion problem and several simulation studies on regression problems show that Clustering Lasso has very good predictive performance and is superior to the Lasso method.

The method was proposed to encourage group effects so that clustered variables are selected together in a model. Clustering Lasso can automatically select groups of variables. If the structural correlation matrix used for regularization is block diagonal matrix, Clustering Lasso is equivalent to the group Lasso proposed by [7] . However, if the relationships among the variables are complicated, we have to simplify the structural correlation matrix to obtain sparse models. We proposed some shrinkage steps to build the desired structural correlation matrix. Rotating the eigen vectors or adapting techniques such as sparse component analysis can also help for this purpose. As a next step, we will use the Clustering Lasso method in the spatial analysis, so that we can maintain the important spatial correlations while selecting sparse models.

Acknowledgements

We thank Mrs. Patricia Andrews for editing the paper.

References