Open Journal of Statistics
Vol.4 No.7(2014), Article
ID:49305,14
pages
DOI:10.4236/ojs.2014.47048
Predictions in Quantile Regressions
Marilena Furno
Department of Agriculture, Università degli Studi di Napoli “Federico II”, Napoli, Italy
Email: marfurno@unina.it
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 June 2014; revised 10 July 2014; accepted 18 July 2014
ABSTRACT
Two different tools to evaluate quantile regression forecasts are proposed: MAD, to summarize forecast errors, and a fluctuation test to evaluate in-sample predictions. The scores of the PISA test to evaluate students’ proficiency are considered. Growth analysis relates school attainment to economic growth. The analysis is complemented by investigating the estimated regression and predictions not only at the centre but also in the tails. For out-of-sample forecasts, the estimates in one wave are employed to forecast the following waves. The reliability of in-sample forecasts is controlled by excluding the part of the sample selected by a specific rule: boys to predict girls, public schools to forecast private ones, vocational schools to predict non-vocational, etc. The gradient computed in the subset is compared to its analogue computed in the full sample in order to verify the validity of the estimated equation and thus of the in-sample predictions.
Keywords:Predictions, Quantile Regressions, Gradient

1. Introduction
Quantile regression is a robust procedure particularly helpful in dealing with asymmetric and with non-normal distributions. It is very useful to evaluate data sets where it is relevant to analyse and estimate a regression model not only at the mean/median of the conditional distribution but also in the tails, measuring the impact of the regressors on the dependent variable at different quantiles.
Besides the estimates of the regression coefficients at different quantiles, the predictions of the model at a given quantile and their summary measures are the focus of the analysis. As the goodness of fit index, an indicator of quantile regression predictive power is a local measure, relative to the specific quantile under analysis. The regression estimates at the selected quantile provide forecasts for that specific quantile, and it may very well be the case that the predictive ability of the model changes at a different quantile: a model may predict the median better than the upper or the lower quantile. The literature on quantile regression predictions is not very extensive. Mayr et al. [1] , for instance, consider quantile regressions to compute predictive intervals. When a new observation for the explanatory variables is available, xn+1, the fitted value computed at the α/2 and 1 ‒ α/2 regression quantiles provide the prediction interval for the explanatory variable, yn+1. In the wheather forecast, the “quantile verification score” (QVS) is implemented, as for instance in Friederichs and Hense, [2] . It is a quantile-specific approach where the forecaster optimises the performance by predicting the “true” quantiles. In what follows a different approach is considered. Different tools to evaluate quantile regression forecasts are proposed and their characteristics are explored and compared. The first is a summary statistic measuring forecast errors. The second is a fluctuation test, based on the quantile regression gradient, which is here considered to evaluate forecasts.
The math scores at the international OECD-PISA test of 15-year-old Italian students are analysed here. The OECD-PISA test has been administered in year 2000, 2003, 2006 and 2009 to verify students’ proficiency. The selected model is estimated by OLS and quantile regression. The purpose is to link student performance to school efficiency. There is a long lasting debate on the role of school variables on student proficiency. Generally speaking, the rate of return to additional years of schooling is large. In addition, growth analysis emphasizes school attainment and shows its high relation to differences in economic growth across countries. Analyses of the relationship between schooling and economic growth by Barro [3] and Mankiw et al. [4] find a significant positive link between quantitative measures of schooling and economic growth. Hanushek [5] relates one standard deviation difference of student performance to a one percent difference in the annual growth rate of per capita gross domestic product, although higher spending in school resources does not necessarily involve higher scores, as discussed in Hanushek and Woessmann [6] .
Therefore, prediction of student performance is one of the possible indicators of economic growth and schooling is one of the elements to improve in order to increase the rate of growth of a country. These analyses generally rely on average values, while policy may be more effective when focusing on the tails, away from the mean. This would be the case of schemes seeking to improve the low scoring in order to rise the general performance. But the analysis of the model on average is not very helpful when the target is to improve the lower tail.
The predictive power of the model is considered by analysing both in-sample and out-of-sample forecasts. To evaluate out-of-sample forecasts the estimates in one wave are employed to forecast the following waves, under the assumption of unchanged model from one wave to the other, that is assuming a fixed coefficient model. The comparison of realizations and predictions based on the estimates of the previous wave provides a measure of the validity of the out-of-sample forecasts at different quantiles. The validity of in-sample forecasts is analysed by comparing the gradient computed in a subset with the gradient computed in the full sample. The following procedure is here proposed:
1) Exclusion of q data from the sample, possibly chosen by a specific selection rule2) Estimation of the model in the selected subset3) Computation of the residuals with respect to this set of estimates for the entire sample4) Comparison of the gradient using these residuals, with the gradient computed in the entire sample.
The model yields good in-sample predictions when such a difference goes to zero. In this case, the model in the subset provides a good approximation for the excluded data, and predictions are good. Vice versa, if the difference between the two sets of results is sizable and cannot be neglected, the subset poorly approximates the excluded observations and the in-sample forecasts are not reliable.
Section 2 summarizes the quantile regression estimator whereas the data and the model are discussed in Section 3. Section 4 presents the data set and Section 5 discusses the results. The last section draws the conclusions. In the Appendix are the Stata codes used to implement the comparison of partial and total sum of the gradient proposed here.
2. Quantile Regression
Consider the linear regression model , where yt is the dependent variable,
, where yt is the dependent variable,
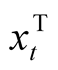 is the p-dimensional row vector of a single observation for the p explanatory variables, et is the error term having continuous and strictly positive density f( ) in a sample of size n. The quantile regression model provides robust estimates of the coefficients and does not require distributional assumptions. Its objective function is given by1:
is the p-dimensional row vector of a single observation for the p explanatory variables, et is the error term having continuous and strictly positive density f( ) in a sample of size n. The quantile regression model provides robust estimates of the coefficients and does not require distributional assumptions. Its objective function is given by1:
 (1)
(1)
where the asymmetric weighting system wt is equal to q for positive errors and to 1 ‒ q for negative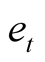 . When q
. When q
= 0.5 the weights are symmetric and the objective function simplifies into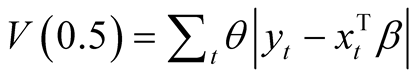 , which provides an estimate of the conditional median regression, or least absolute deviation (LAD). Often the median regression estimates do not significantly differ from the conditional mean regression (OLS), and this is the case with symmetric conditional distributions. The advantage of quantile regression relies in the possibility of investigating the dependent variable at many points of the conditional distribution, not only at the centre but also in the tails.
, which provides an estimate of the conditional median regression, or least absolute deviation (LAD). Often the median regression estimates do not significantly differ from the conditional mean regression (OLS), and this is the case with symmetric conditional distributions. The advantage of quantile regression relies in the possibility of investigating the dependent variable at many points of the conditional distribution, not only at the centre but also in the tails.
The predictions of the quantile regression model are then analysed. Forecast in quantile regression, just as the goodness of fit index, can be considered a local measure, relative to the specific quantile under investigation. In the following sections predictions for one wave based on the estimates computed in the previous wave provide out-of-sample forecasts, while predictions within each wave provide in-sample forecasts for a given quantile regression.
A first approach is to compute a summary measure of forecast error and, among the various existing statistics on predictions, the mean absolute deviation of forecasts from realizations, MAD, is here considered. Quantile regressions are based on the l1 norm, therefore MAD seems the appropriate index to summarise the predictive power in quantile regressions, particularly so at the median. The statistic is given by:
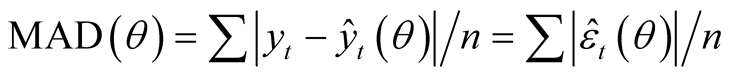 (2)
(2)
where
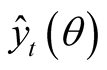 are the fitted values computed at the selected quantile and
are the fitted values computed at the selected quantile and
 are the prediction errors at the quantile θ.
are the prediction errors at the quantile θ.
In addition, to verify the reliability of the in-sample forecasts it is possible to consider the comparison between partial and total sum of the gradient. This comparison, considered by Qu [12] and by Oka and Qu [13] to define a changing coefficient test and by Xiao [14] for a test of cointegration, focuses on the quantile regression gradient
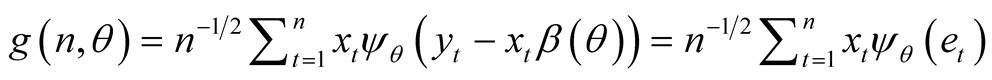 (3)
(3)
where
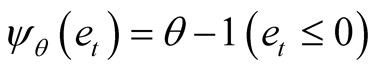 is the sign function. In a subset of size n1, the gradient (n1,q), is:
is the sign function. In a subset of size n1, the gradient (n1,q), is:
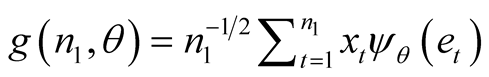 (4)
(4)
and a function of the gradient, considered for both n and n1 sample sizes, is defined as
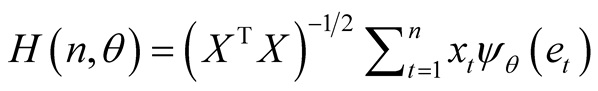 (5)
(5)
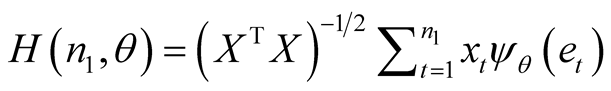 (6)
(6)
where X is the (n, p) matrix of explanatory variables. The comparison of H(n1,q) and H(n, q) is provided by the following test function defined in Qu [12] :
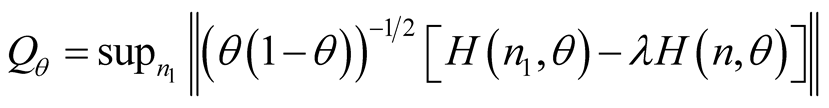 (7)
(7)
where
 is the sup norm selecting the maximum difference between H(n1,q) and H(n,q) within the entire vector of coefficients and l = n1/n is the proportion of data in the subset. The gradient estimated in the n1 subset, yielding H(n1,q), is compared with the gradient estimated in the full sample H(n,q). In case, H(n1,q) is a good proxy for H(n,q), the in-sample predictions are reliable. Vice versa, when the model is inadequate H(n1,q) and H(n,q) diverge and the in-sample forecasts are unreliable. In addition, the sample of size n can be split into n = n1 + q by choosing a specific selection rule related to the variables of the equation: for instance in n1 the public funded schools can be selected and compared to the private ones, or the schools located in the southern regions compared to all the other schools. A relevant discrepancy would signal poor forecasts due to a statistically significant gap between the two subsets. The model is separately estimated in the subset and in the full sample. The residuals from the regression estimated in the n1 subset are compared to the residuals estimated in the entire sample through the H(n1,q) and H(n,q) functions. If they do not significantly differ the in-sample forecasts of the model based on that specific selection rule are reliable and there is no gap between the subset and the entire sample.
is the sup norm selecting the maximum difference between H(n1,q) and H(n,q) within the entire vector of coefficients and l = n1/n is the proportion of data in the subset. The gradient estimated in the n1 subset, yielding H(n1,q), is compared with the gradient estimated in the full sample H(n,q). In case, H(n1,q) is a good proxy for H(n,q), the in-sample predictions are reliable. Vice versa, when the model is inadequate H(n1,q) and H(n,q) diverge and the in-sample forecasts are unreliable. In addition, the sample of size n can be split into n = n1 + q by choosing a specific selection rule related to the variables of the equation: for instance in n1 the public funded schools can be selected and compared to the private ones, or the schools located in the southern regions compared to all the other schools. A relevant discrepancy would signal poor forecasts due to a statistically significant gap between the two subsets. The model is separately estimated in the subset and in the full sample. The residuals from the regression estimated in the n1 subset are compared to the residuals estimated in the entire sample through the H(n1,q) and H(n,q) functions. If they do not significantly differ the in-sample forecasts of the model based on that specific selection rule are reliable and there is no gap between the subset and the entire sample.
Furthermore, the comparison between partial and total sum of the gradients is analyzed separately for each regression coefficient and the convergence/divergence between H(n1,q) and H(n,q) becomes a diagnostic tool to explore the validity of each explanatory variable for predictive purposes. In detail, the equation is estimated twice, in the n1 subset and in the full sample. From the two estimated equations two sets of n residuals are computed2. The former, computed in the subset, provides an estimate of H(n1,q), while the latter allows to evaluate H(n,q). The behavior of this divergence spells out whether the selected subset is fit or unfit to predict the q omitted observations. The comparison of the gradients becomes a diagnostic tool to gauge the validity of each variable and thus the predictive capability of the selected model.
3. The Model
The OECD-PISA test of Italian students has been administered in year 2000, 2003, 2006 and 2009. The different waves of the test are taken into account and the score of the test is related to explanatory variables describing school characteristics like school size, funding, supplied services, student teacher ratio. The purpose is to link student performance to school efficiency. The model is estimated not only at the mean but also in the tails of the conditional distribution, considering low and high proficiency students as well. There is a wide-ranging debate on the role of school variables on student proficiency. Growth analysis emphasizes school attainment and shows its high relation to differences in economic growth across countries. The mathematical skill, in particular, is considered a good proxy of labour force quality. Hanushek [5] relates one standard deviation difference of student performance to a one percent difference in annual growth rate of per capita gross domestic product. However, higher spending in school resources does not necessarily involve higher test scores, as discussed in Hanushek and Woessmann [6] .
The model here considered explains the scores on the math tests as a function of region—a dummy variable taking unit value for the southern regions to capture the existing lag in the southern economy; funding—a dummy variable taking unit value for private schools, which in Italy are in a small number and mostly remedial; school track—which distinguishes academic from technical and from vocational fields by means of dummy variables; gender—a dummy taking unit value for boys who, generally speaking, improve upon girls in math while worsen in reading proficiency; school size—providing the number of students enrolled; number of computers in the school; student-teacher ratio; proportion of certified teachers in the school; shortage of teachers in the school; the four categorical variables on poor library facilities, shortage of computers, shortage of textbooks, shortage of laboratory equipment. These four variables take the categories of: a lot, some, a little, not at all. They are transformed in numerical variables by assigning decreasing values from 4 to 1, assigned respectively to the category “a lot” and “not at all”. The sample comprises n = 52,067 observations. Table 1 presents few summary statistics of the dependent variable: sample size, mean, standard deviation, 10th, 50th and 90th quantile in each wave of the
Table 1 . Math scores, summary statistics.
data set. The mean and the median reach a peak on 2003 then decline to raise again in 2009. The median is always larger than the mean, signalling skewness. The 10th quantile over time has increased more than the 90th, as can be seen by comparing the score in 2000 and 2009 at the selected quantiles: math(0.10)2009 ‒ math(0.10)2000 = ∆(0.10)2009-00 = 42.32, math(0.50)2009 ‒ math(0.50)2000 = ∆(0.50)2009-00 = 22.71, math(0.90)2009 ‒ math(0.90)2000 = ∆(0.90)2009-00 = 23. This shows a greater improvement of the lower scoring students over time. However, the greatest improvement occurs from wave 2000 to 2003 at the top quantile, with a gain in the scores of highly proficient students equal to ∆(0.90)2003-00 = 59.63.
The following analysis compares OLS and quantile regression results, and the comparison is particularly useful with asymmetric distributions since it allows to consider the impact of school resources in the tails that is at several levels of student proficiency. The issue of the role and impact of school resources on student proficiency is highly debated, and this impact is hardly homogeneous across quantiles. The selected quantiles-proficiency levels are the 10th, 50th and the 90th quantile3.
4. OLS and Quantile Regression Estimates
Table 2 presents the OLS and the median regression estimates. The regional variable is negative, reflecting the lag of southern regions; the school track yield positive estimates, showing that academic and technical schools improve upon the vocational schools; the gender variable has a positive sign; the private schools have a negative impact, confirming their remedial nature; school size is negative but small; shortage of computers and student teacher ratio have a positive sign; the remaining variables are mostly non-statistically different from zero. The impact of school resources on students’ performance is highly debated in the literature. These results are in line with those works ruling out any effect of school inputs, like class size or student-teacher ratio, on students performance—see for instance Hanushek [5] orHanushek and Woessmann [6] . The comparison of left and right hand sides’ results of Table 2 shows that the median provides results mostly inside the ±2s confidence interval of the OLS coefficients, thus the median is not significantly different from the mean regression (OLS). The underlined coefficients, which are those statistically different from their OLS analogues, are the estimates of private, regional and school size parameters.
Table 3 reports the results of the 10th and the 90th quantiles. This table presents many more underlined values that are quantile regression estimates laying outside the ±2s OLS confidence intervals. The implication is that both the low and the top scoring students are poorly represented by the conditional mean, the OLS regression. There are however differences from one tail to the other, like for instance the negative impact of private schools is much stronger at the 10th than at the 90th quantile. The underlined and significant coefficients cluster in the upper part of this table, signalling regional variable, gender, school track and funding as the main variables affecting math scores at both ends of the conditional distribution.
This result is confirmed by the interquantile differences, which compute changes across quantiles and verify if a discrepancy between estimated coefficient at two different quantile regressions is statistically significant. The differences between the 90th and the 50th quantile together with the difference between the 10thquantile and the median are reported in Table4 It turns out that these differences are mostly explained by the regional variable—particularly in the 90th - 50th interquantile difference, and by funding, gender, school track in both 90th - 50th and 50th - 10th interquantile comparisons. The regional variable improves in going from the median to the top quantile signalling a reduced regional gap at the higher quantiles. The improvement in math scores granted by the non-vocational schools, both academic and technical, is greater at the first quantile with respect to the median and greater at the median with respect to the 90th quantile; this causes a negative sign for these coefficients in the interquantile differences; furthermore the increments are larger at the median versus the 90th quantile than at the 10th versus the median. Gender improves in going from the median to the top 90th quantile with improvements occurring in every wave but in 2009. The negative impact of private funded schools improves at the median with respect to the first quantile in 2006 and 2009, while is less relevant in explaining the 90th - 50th interquantile difference, since it is significant only in year 2009. The remaining variables either do not explain any of the changes across quantiles—as occurs for the variables number of computers in the school, school size, shortage of teachers and shortage of textbooks—or are significant in explaining the interquantile differences only in one wave—as in the case of proportion of certified teachers, poor library facilities, shortage of laboratory equipment, shortage of computers, student-teacher ratio.
Table 2 . OLS and median regression estimates in each wave and in the entire sample.
Note: Absolute value of t-statistics in parentheses. Underlined are the quantile regression estimates outside the ±2s OLS confidence intervals.
Table 3. First and last quantile regression estimates in each wave and in the entire sample.
Note: Absolute value of t-statistics in parentheses. Underlined are the quantile regression estimates outside the ±2s OLS confidence intervals.
Table 4. Interquantile difference between 50th - 10th and 90th - 50th quantiles.
Note: Absolute value of t-statistics in parentheses.
5. Results
Table 5 reports the summary statistics of quantile regressions predictive power of the out-of-sample forecasts. The first three rows of the table consider year 2000 estimated coefficients at the 10th, 50th and 90th quantile regressions to predict years 2003, 2006 and 2009, that is using first wave to predict the following ones. Rows four to six consider year 2003 to predict years 2006 and 2009. In rows seven to nine, the forecast of year 2009 is based on the quantile regression estimated coefficients of year 2006. The comparison of observed and predicted
Table 5 . Assessment of OLS and quantile regression out-of-sample forecasts.
Note: The first three rows use estimates of year 2000 at the 10th, 50th and 90th quantile regression to compute predictions for wave 2003, 2006 and 2009. The second group of three rows utilizes estimates of year 2003, while the third group considers estimates of year 2006 to forecast next waves. The first group of three columns considers quantile regression estimates while the second group of three columns computes predictions based on the OLS estimates.
values in MAD(q), reported in the first three columns of this table, shows that the forecasts are more precise at the median than in the tails, the estimated coefficients for year 2000 yield worse forecasts at the lower quantile while the estimates of 2003 worsen at the upper quantile. The second group of three columns of the table report the MAD values computed by OLS, MADOLS. These results are quite comparable with the median regression values, yielding only minor differences.
In order to analyse in-sample forecasts, consider the model estimated in the entire sample, pooling together year 2000, 2003, 2006, 2009. Last column of Table 2 reports the results for the median regression, where the estimated coefficients not statistically different from zero are in italics. These variables—shortage of lab equipment, poor library facilities, shortage of teachers and proportion of certified teachers—are dropped from the model, in order to provide a more parsimonious specification. The results for this parsimonious model as estimated at the median regression are reported in the last column of Table6 The elimination of these four variables allows to increase the number of available observations to n = 56,856.
The previous analysis shows that regional variable, gender, school track and funding are the main regressors affecting interquantile changes in math scores, and these variables provide the criteria to select the sample. In time series it is easy to exclude the final observations, and the sole decision is on the number of excluded observations q. The data here considered are not time series and, instead of dropping the last observations of the sample, it is more informative to define a criterion to select the q subset. In principle, any explanatory variable could provide a systematic rule to exclude data points, but the analysis is here limited to the four above mentioned variables which proved to cause the greater interquantile differences.
Consider first the regional variable. In this case the score of students of the northern regions, in a sample of size n1 = 36,369, are chosen to forecast southern students performance. This means to select 64% of the sample, in order to forecast the remaining 36% of the data. Data are sorted so that northern students are at the beginning of the sample and the same model is estimated twice: in the full sample and in the subset of northern students. The estimates in the entire sample are reported in the first column of Table 6, and the regional variable in this column is dropped from the model4. From the estimates in the subset, the n residuals are computed and the difference between total and partial sum of the gradients can be analysed as n1 converges to n. The difference between H(n1,q) and H(n,q) as n1 approaches n, for each regression coefficient, is reported in Figure 1 which depicts the pattern for each regression coefficient. In the figure the n1 subset is to the left of the vertical line, which in the graph marks the passage from the n1 subset to the qexcluded observations. The graph shows that partial and total
Table 6 . Median regression estimates in the entire sample to evaluate predictions.
Note: Absolute value of t-statistics in parentheses. In italics are the estimates with low t-values. The variable selected to define the n1 subset is dropped from the equation. In the subset it is automatically dropped. If it is included in the full sample equation and excluded in the subset equation, the difference between total and partial sum of gradients could be due to the different number of regression coefficients and not, or not only, to the adequacy of the model.
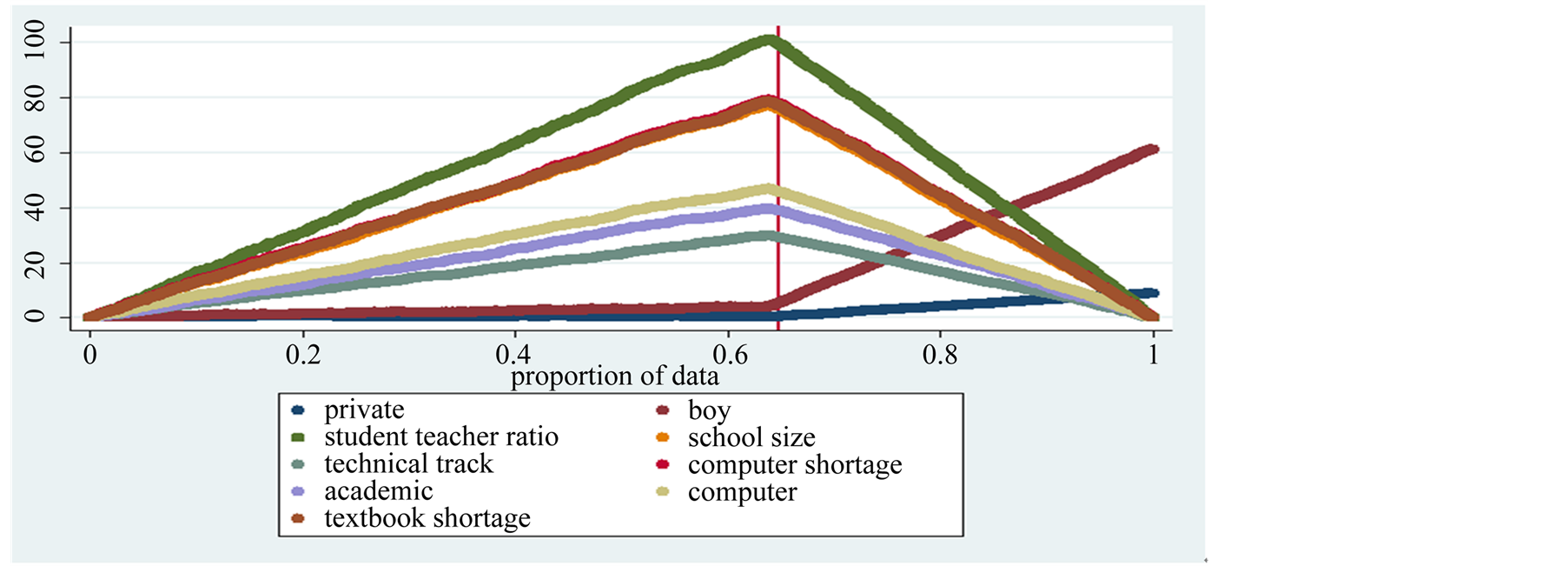
Figure 1. The graph compares partial and total sum of the gradient of each estimated coefficient in case northern student performance is considered to forecast southern student performance for year 2000, 2003 2006, and 2009 pooled together. This leaves out to predict about 64% of the sample. The differences to the right of the vertical bar, which signals the q predicted observations, converge to zero for all coefficients but those of funding and gender, which are not good predictors of math score of southern students, data OECD-PISA.
sum of the gradient for the regression coefficients, after reaching a peak at the end of the n1 subset, converge toward zero. The exceptions are gender and funding, which diverge after the vertical bar signalling the beginning of the q subset. This implies that the performance of northern boys does not predict well southern girl scores and that northern student are not good predictors for southern student enrolled in private schools.
Next the gender variable is selected to define the n1 subset. Boys’ scores in math test are used to forecast girls’ performance. Gender is a relevant explanatory variable and this criterion splits in half the sample, excluding q = 28540 observations, which is about 50% of the sample. The second column of Table 6 presents the estimates in the entire sample, where with respect to the parsimonious model the gender variable has been excluded5. Boys math scores are sorted at the beginning of the sample. The predictions of girl scores based on boys performance yield an increasing difference between H(n1,q) and H(n,q) up to n1, and then a decreasing difference after the vertical bar, as can be seen in Figure 2. This occurs for all gradients but the regional and the funding coefficients, thus implying that setting aside gender differences in performance, region and funding make a big difference and cause poor forecasts.
The third column of Table 6 presents the estimated equation excluding academic and technical track variables, where data have been sorted to have scores from the vocational track at the beginning of the sample6. The same regression is estimated in a subset of size n1 = 12,387 which considers the vocational schools only. The set of n residuals from this equation are computed in order to evaluate predictions for the remaining 78% of the sample, which represents students enrolled in non-vocational tracks. Figure 3 presents the comparison of total and partial sum of the gradients as n1 → n. In this graph, the discrepancy between the two sets of gradients goes to zero as n1 increases, with the sole exception of the regional and funding coefficients. The scores of students enrolled in vocational schools are not good predictors of southern students’ performance and of private schools learners’ scores.
Finally, the same approach is implemented considering the public school sector to forecast the performance of students enrolled in private schools. The number of excluded observations in this experiment is quite small, approximately 3.6% of the sample. The estimates for the entire sample are presented in the last column of the table—headed “funding”7. It turns out that students of public schools well predict math scores of both public and

Figure 2. The graph depicts the comparison between partial and total sum of the gradient of each estimated coefficient in the regression considering only boys to forecast girls performance in year 2000, 2003, 2006, 2009 pooled together. This leaves out to predict 49.08% of the sample. The patterns to the right of the vertical bar, which signals the predicted observations, decline toward zero for all the regression coefficients with the exception of the regional and private variables, which do not help in predicting math score of girls, data OECD-PISA.
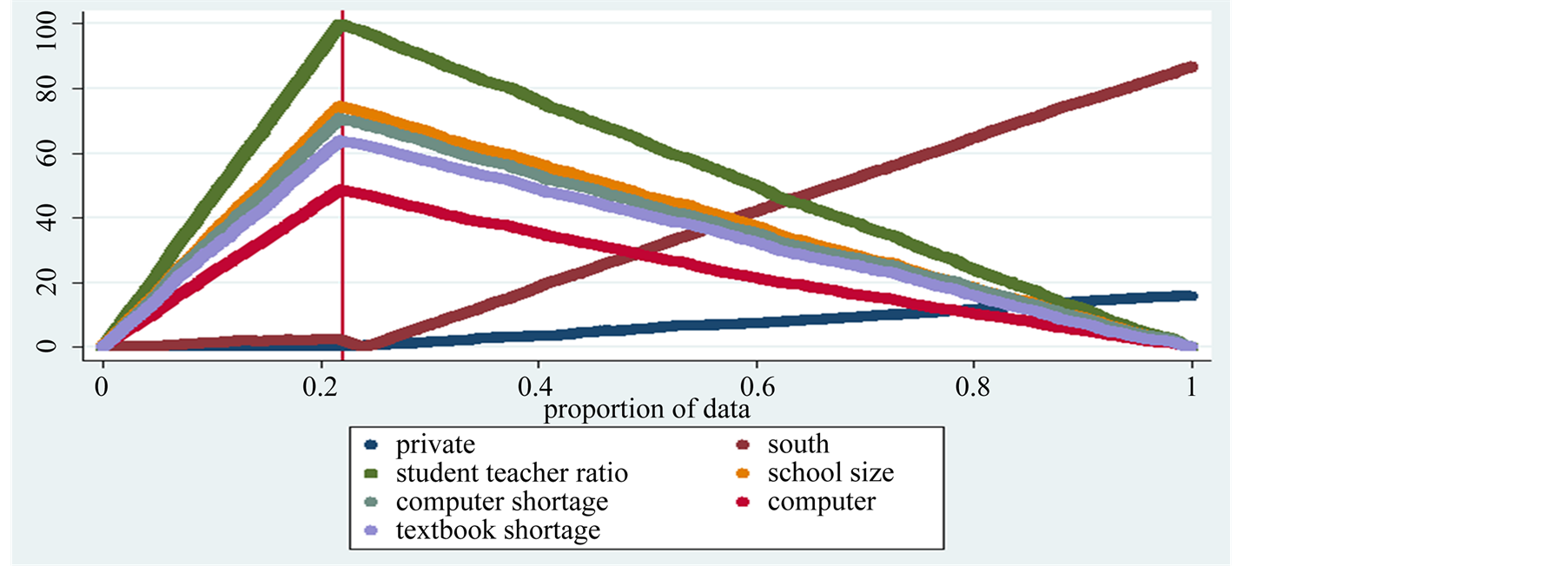
Figure 3. The graph depicts the comparison between partial and total sum of the gradient of each estimated coefficient in the regression considering vocational schools to forecast performance in academic and technical track schools for the years 2000, 2003, 2006, 2009 pooled together. This leaves out to predict 78% of the sample. The patterns to the right of the vertical bar, which signals the q predicted observations, decline toward zero for all the regression coefficients with the exception of the regional and private variables, data OECD-PISA.
private schools with the exception of the regional and gender variables. That is, math scores of public schools students are poor predictors of southern students and of girls performance. The graph in Figure 4 shows the divergence between total and partial sum of the gradient, and the regional and the gender variable diverge after the vertical line marking the q excluded observations, while the discrepancy between H(n1,q) and H(n,q) in all the other coefficients goes to zero after the vertical line.
Summarizing, Table 6 considers region, gender, track and funding as sample selection rules to evaluate insample forecasts, since in the interquantile difference analysis these variables cause the greater changes in the estimated coefficients at the selected quantiles. The first three variables, region, gender and track, exclude about 50%, 64% and 78% of the observations, while funding excludes a very small number of data, only 3%. This is to say that the results do not depend upon the number of excluded observations. On the overall, the graphs show that the coefficients causing the greatest divergence between total and partial sum of the gradient are region, gender and funding, and their impact is mutually influenced: when selecting private schools, the regional and the gender variables are unreliable predictors; when selecting the northern region, gender and funding are the most diverging terms; when gender and school track provide the sample selection rule, both region and funds are poor predictors.
6. Conclusions
The math scores of the OECD-PISA test have been investigated at different quantiles, to analyse the impact of school resources on students’ proficiency. School attainment is related to differences in economic growth, while mathematical skill is considered a good proxy of labour force quality. These links are generally discussed in terms of average values while quantile regressions also allow to investigate the tails of the conditional distribution. The estimated coefficients do differ across quantiles, which implies that the tails of the math score distribution behave quite differently from the central model as computed by OLS. Thus, the analysis of the model on average is not very helpful when the aim is to improve one or both tails.
The forecast ability of the model has been considered. The literature on quantile regression predictions is not very extensive. The above analysis considers the median absolute deviation, MAD(q), computed as the difference between predicted and observed data to evaluate quantile regression forecasts. The MAD(q) results show that the predictive power of quantile regressions improves at the median for out-of-sample forecasts, and that forecasts computed at the median are comparable with OLS predictions.
To evaluate in-sample forecasts some data points are excluded from the sample. The previous sections consider the exclusion based on a specific selection rule, related to the variables of the model. Four different criteria to select the sample have been considered: southern students to predict students living in the rest of the country;
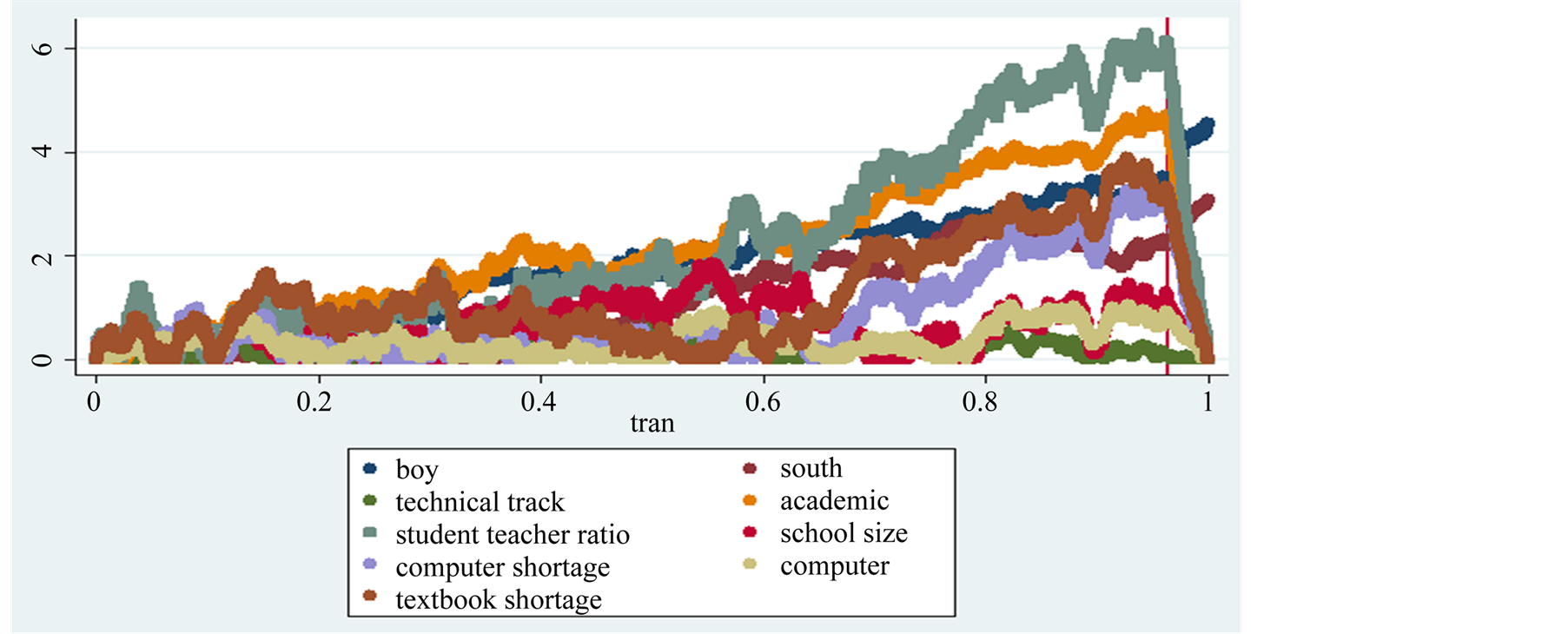
Figure 4. The left hand side of this figure depicts the comparison between partial and total sum of the gradients of each estimated coefficient in the regression considering public schools to forecast private schools for the years 2000, 2003, 2006, 2009 pooled together. This leaves out to predict 3.6% of the sample. The patterns to the right of the vertical bar point out the q predicted observations, and show a discrepancy for the regional and the gender variables, data OECD-PISA.
boys to predict girls performance; vocational track to forecast performance of students enrolled in the other curricula; students enrolled in public school to forecast performance of private schools students. Each of the four criteria selects a different subset. The data are appropriately sorted locating the selected subset at the beginning of the sample. The model is estimated in the full sample and in the subset. The vector of gradients estimated in the subset is compared with its analogue in the full sample. The model yields good in-sample predictions when such a difference, computed individually for each regression coefficient, goes to zero. Indeed, if the gradients are similar, the predictions generated by the selected subset are reliable. Vice versa, when the two gradients are far apart, the subset poorly predicts the excluded data, signalling a significant gap between the two subsets. The diagnostic tool here implemented to check in-sample forecasts shows that, while for most variables the gradient in a subset does not diverge much from its analogue in the full sample, thus granting good predictions, the predictive capability of the regional, gender and funding variables is quite unreliable.
References
- Mayr, A., Horthorn, T. and Fenske, N. (2012) Prediction Intervals for Future BMI Values of Individual Children—A Non-Parametric Approach by Quantile Boosting. BMC Medical Research Methodology, 12, 1-13. http://dx.doi.org/10.1186/1471-2288-12-6
- Friederichs, P. and Hense, A. (2007) Statistical Downscaling of Extreme Precipitation Events Using Censored Quantile Regression. Monthly Weather Review, 135, 2365-2378. http://dx.doi.org/10.1175/MWR3403.1
- Barro, R. (1997) Determinants of Economic Growth: A Cross-Country Empirical Study. MIT Press, Cambridge.
- Mankiw, N., Romer, D. and Weil, D. (1992) A Contribution to the Empirics of Economic Growth. Quarterly Journal of Economics, 107, 407-437. http://dx.doi.org/10.2307/2118477
- Hanushek, E. (2006) School Resources. In: Hanushek, E.A. and Welch, F., Eds., Handbook of Economics of Education, Vol. II, North Holland, Amsterdam.
- Hanushek, E. and Woessmann, L. (2011) The Economics of International Differences in Educational Achievement. In: Hanushek, E.A., Machin, S.J. and Woessmann, L., Eds., Handbook of Economics of Education, Vol. III, North Holland, Amsterdam.
- Koenker, R. and Bassett, G. (1978) Regression Quantiles. Econometrica, 46, 33-50. http://dx.doi.org/10.2307/1913643
- Koenker, R. (2005) Quantile Regression. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511754098
- Koenker, R. and Machado, J. (1999) Goodness of Fit and Related Inference for Quantile Regression. Journal of the American Statistical Association, 94, 1296-1310. http://dx.doi.org/10.1080/01621459.1999.10473882
- Davino, C., Furno, M. and Vistocco, D. (2014) Quantile Regression: Theory and Applications. Wiley, Hoboken.
- Hao, L. and Naiman, D. (2007) Quantile Regression. Sage, London.
- Qu, Z. (2008) Testing for Structural Change in Regression Quantiles. Journal of Econometrics, 146, 170-184. http://dx.doi.org/10.1016/j.jeconom.2008.08.006
- Oka, T. and Qu, Z. (2011) Estimating Structural Changes in Regression Quantiles. Journal of Econometrics, 162, 248-267. http://dx.doi.org/10.1016/j.jeconom.2011.01.005
- Xiao, Z. (2009) Quantile Cointegrating Regression. Journal of Econometrics, 150, 248-260. http://dx.doi.org/10.1016/j.jeconom.2008.12.005
NOTES

1For further details see Koenker and Bassett , Koenker , Koenker and Machado , Davino et al. , Hao and Naiman .

2The coefficients estimated in the n1 subs et al. low to compute the residuals for both the n1 included and the q excluded observations, so that the comparison between H(n1,θ) and H(n,θ) can be implemented as n1 → n.

3The estimates computed at additional quantiles are available on request.

4The model estimated in the subset will automatically drop the regional variable, since in the subset there are only southern students. In case the regional variable is not excluded from the full sample model, the number of explanatory variables will differ in the two equations, and this would make them unsuitable for the comparison of H(n1,θ) and H(n,θ). The inclusion of the variable clouds the results, since a divergence between the H functions can be due to the different number of coefficients and not, or at least not only, to the predictive capability of the model.

5The model estimated in the subset will automatically drop the gender variable, since in the subset there are only boys. Therefore, the gender variable is dropped from the full sample equation as well, otherwise the number of explanatory variables in the two models would differ and the comparison of H(n1,θ) and H(n,θ) would be inappropriate.
6Once again the exclusion of the academic and the technical variable from the parsimonious model estimated in the entire sample is needed in order to have the same number of variables in the two different estimates of the model, so that H(n1,θ) and H(n,θ) are comparable.
7The variable private has been excluded from the parsimonious equation estimated in the entire sample, in order to accurately compare H(n1,θ) and H(n,θ).


