Open Journal of Statistics
Vol.3 No.6(2013), Article ID:41530,8 pages DOI:10.4236/ojs.2013.36046
Precision Analysis and Parameter Inversion in the Stepwise Deployment of a Mixed Constellation
College of Science, National University of Defense Technology, Changsha, China
Email: isabellayj@gmail.com
Copyright © 2013 Jing Yao. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property Jing Yao. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
Received August 21, 2013; revised September 21, 2013; accepted September 28, 2013
Keywords: Satellite Navigation System; Stepwise Deployment; Weighted Dilution of Precision; Positioning Precision; System Evolvement
ABSTRACT
Along with the planning and implementation of the COMPASS satellite navigation system, first as a regional then a global system, there is a need to probe into the positioning performance of the mixed constellation in the stepwise deployment scheme. Both the increase in the number of the MEO satellites in the constellation and the decrease in the user equivalent ranging error of the GEO satellites will improve the overall positioning performance of the system. Using the weighted dilution of precision as the evaluation criterion, we study the theoretical relationship between the internal parameters and the positioning precision during the evolution of the system. On one hand, the influence of each factor on the positioning performance is quantitatively analyzed under the circumstances of various constellation deployment schemes and user types. On the other hand, for given positioning performance indices, simulations are carried out to present the inversion of parameters. Our conclusions provide useful suggestions to the system design and stepwise deployment scheme of satellites.
1. Introduction
Global Navigation Satellite systems (GNSS) are very important spatial information infrastructure. To further enhance the regional positioning performance, non-uniform mixed constellations have been more widely accepted for the design of satellite navigation systems in recent years. They are constructed to meet the demand of the global navigation and the increasing need of the regional performance [1]. Consequently, the hybrid constellation design is now applied by using different types of satellites, such as the geostationary (GEO), inclined geosynchronous (IGSO), and medium Earth orbit (MEO) satellites.
Currently, new satellites are added to the United States and European constellation resources to establish regional augmentation systems. Navigation augmentation systems, such as WAAS and EGNOS, broadcast augmentation signals using GEO satellites to reduce or eliminate factors that deteriorate the quality of position, navigation, timing services and also enhance reliability and integrity of the system. In 2000, China developed its Compass Navigation Test System, which has created significant impacts in all aspects of people’s life and Chinese society. To better serve the development of the nation and to meet the needs of global applications, China has started the construction of the Compass Navigation Satellite System (simply called COMPASS or Beidou). The COMPASS system will expand into a global system from a regional start, constantly improve its quality of service, and materialize a seamless development between construction stages. The constellation consists of GEO, IGSO and MEO satellites. These different kinds of satellites will jointly perform the functionality of the mixed constellation [2]. So far, sixteen COMPASS satellites have been successfully launched and well maintained in orbit (www.beidou.gov.cn).
Affected by many factors, such as manufacture of satellites, launch capability and precision of the orbits, the GNSS construction covers a rather long period of time. An appropriate stepwise deployable architecture should be able to adapt to the constraints such as cost, verification and scheduling. Some efforts have been made during past years on developing platforms of design, analysis and simulation for satellite constellation deployment strategies [3]. As a helpful tool at the system design level, this kind of platform usually focuses on providing convenient manipulation and demonstration interface. Among the enormous factors to be taken into consideration, positioning performance is one of the basic premises of GNSS applications. Therefore, it is necessary to consider the system’s positioning performance throughout the stages of planning, construction and stepwise deployment [4]. It takes time to launch each satellite, while the increasing number of satellites plays a vital role in enhancing the overall performance of the system. On the other hand, with improved precision of satellites orbits, users’ demands on the system performance are also greatly satisfied. In this paper, in order to provide a reference for the implementation of the stepwise deployment scheme, we analyze the evolution of the positioning performance during the system construction by extracting the internal factors that affect the positioning precision. Then, we inversely derive the requirements of these factors.
2. Motivation
2.1. Relationship between Stepwise Deployment and Positioning Performance
On the basis of the first generation Compass test system, COMPASS is currently composed of mixed types of satellites, among which the GEO and IGSO satellites achieve mainly regional coverage, while MEO satellites will be gradually launched to provide the ultimate global coverage. As COMPASS evolves from a regional system to a global one, the increasing number of MEO satellites in the constellation will enhance the coverage for the users, gradually improve the viewing geometry, and thus upgrade the overall positioning precision [5].
Additionally, in terms of the orbit precision of the navigation satellites, different types of navigation satellites have various orbital characteristics, which lead to unequal orbit determination errors, extrapolation errors and broadcast ephemeris precisions. Speaking more generally, there are rather large differences in the users’ equivalent ranging errors (UERE) for different types of satellites [6]. For instance, the GEO satellites are relatively static to the tracking stations. This essentially makes the orbit determination geometry remain the same, thus the clock errors are difficult to separate. Moreover, GEO orbits are more sensitive to the radiation pressure so that extrapolation cannot be too long ahead. Therefore, under the same conditions the ranging error introduced by the GEO satellites ephemeris is greater than those of MEO and IGSO satellites. As of this writing, the orbit determination for GEO satellites is still a prime difficulty for applications of the system. It may even become the bottleneck that determines whether or not GEO satellites can participate in the navigation and positioning operation along with other types of satellites within the whole constellation. Many research efforts have been made to improve the precision of orbit determination for GEO satellites [7-9].
Therefore, with the ongoing stepwise deployment of the COMPASS constellation, the positioning performance of the system can be improved in at least two aspects: new satellite launches that will enhance the system structure by gradually increasing the number of MEO satellites, and advances in the receiver technology and information processing techniques that can reduce the UERE of GEO satellites. The motivation of this paper is to study the evolution of the positioning performance of the system throughout the COMPASS constellation deployment in terms of these two aspects.
2.2. The Weighted Dilution of Precision
In view of that different navigation satellites in the mixed constellation carry different error characteristics in their own ranging information, we choose the weighted dilution of precision (WDOP) as an evaluation criterion to study the relationship between the internal factors and the positioning precision in the system evolution process. WDOP can assign corresponding weights to the observations according to the ranging errors of each navigation satellite in the case of unequal-precision measurements. It is often used in the evaluation of the system positioning performance and satellite selection because it is more objective than the general DOP (dilution of precision) [10-12].
Suppose that at a certain instant there are m visible navigation satellites, among which there are respectively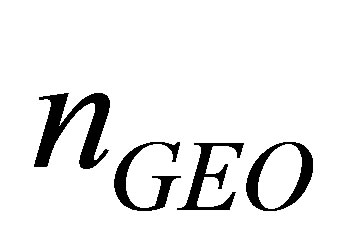 ,
, 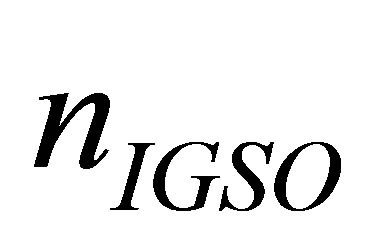 , and
, and 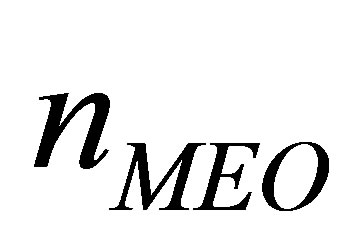 satellites of different types in sight so that
satellites of different types in sight so that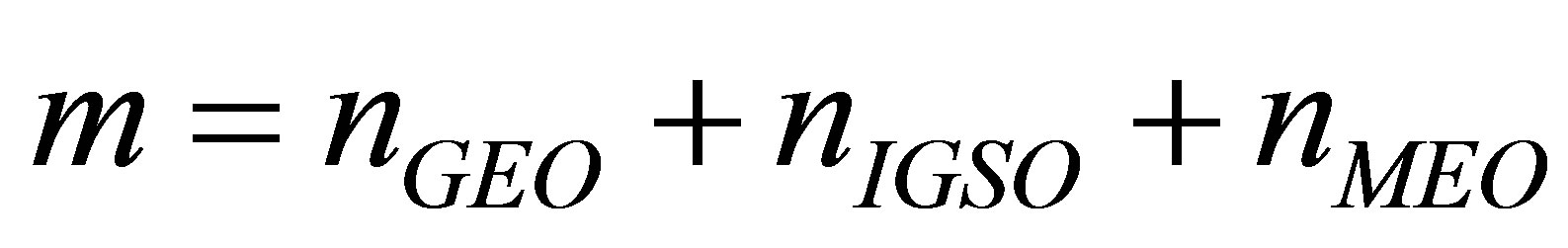 . Then linearizing the nonlinear pseudo-range observation equations leads to the following design matrix
. Then linearizing the nonlinear pseudo-range observation equations leads to the following design matrix
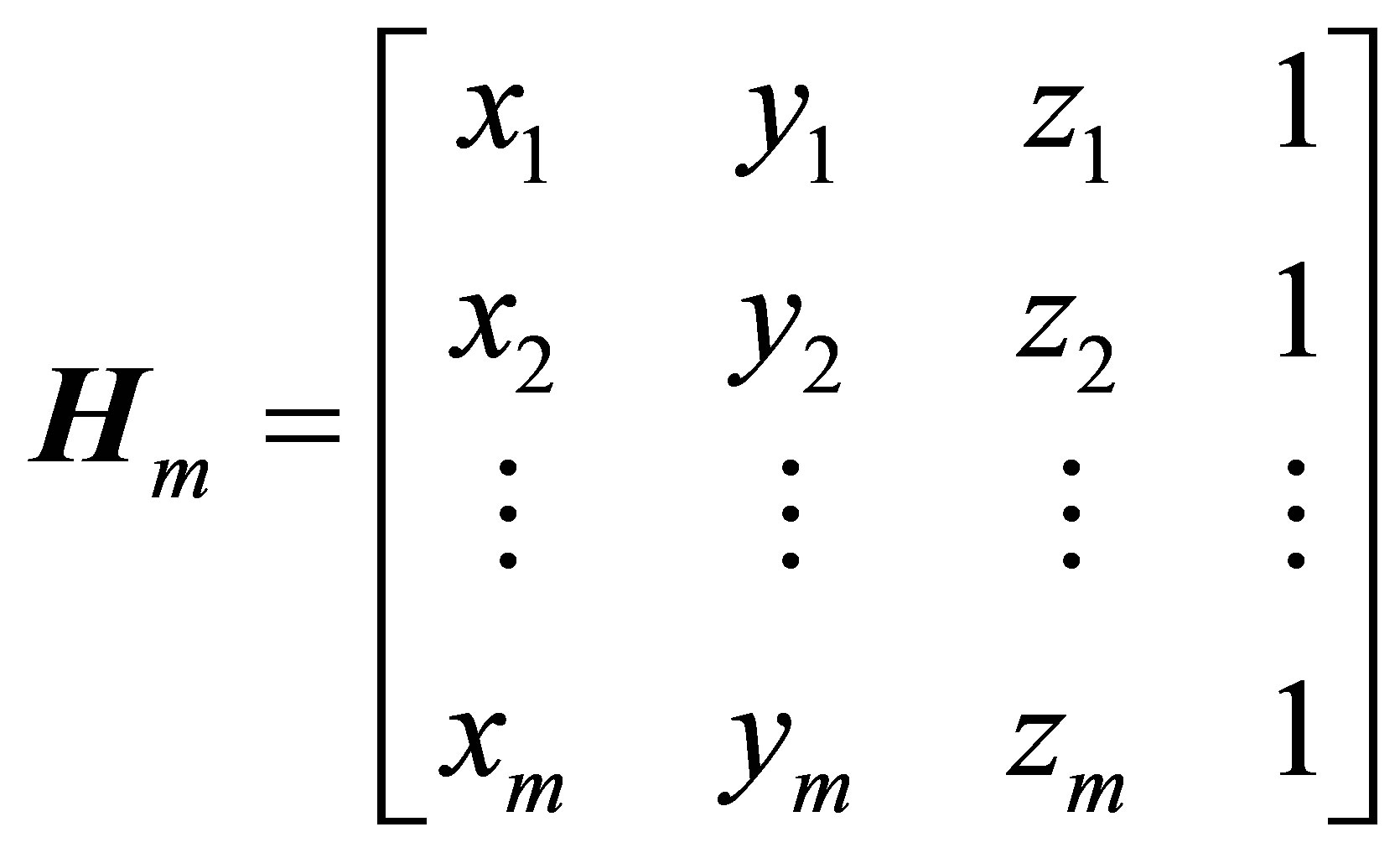 , (1)
, (1)
where  is the unit directional vector between satellite-i and the approximate location of the user receiver and satisfies
is the unit directional vector between satellite-i and the approximate location of the user receiver and satisfies
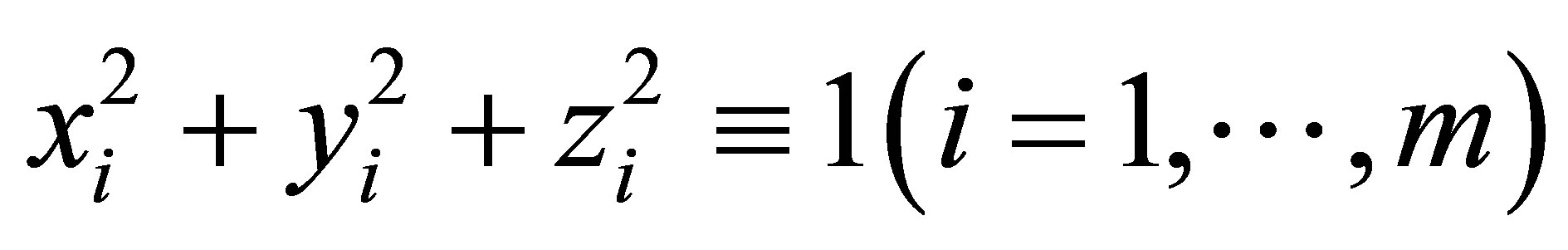 , (2)
, (2)
where “ ” represents “always equal”. Then the WDOP can be defined as
” represents “always equal”. Then the WDOP can be defined as
 , (3)
, (3)
where Tr(·) is the trace of the matrix, and  is the weight matrix, which can be chosen as follows. In the case of independent observations, assume that the squared UERE value
is the weight matrix, which can be chosen as follows. In the case of independent observations, assume that the squared UERE value 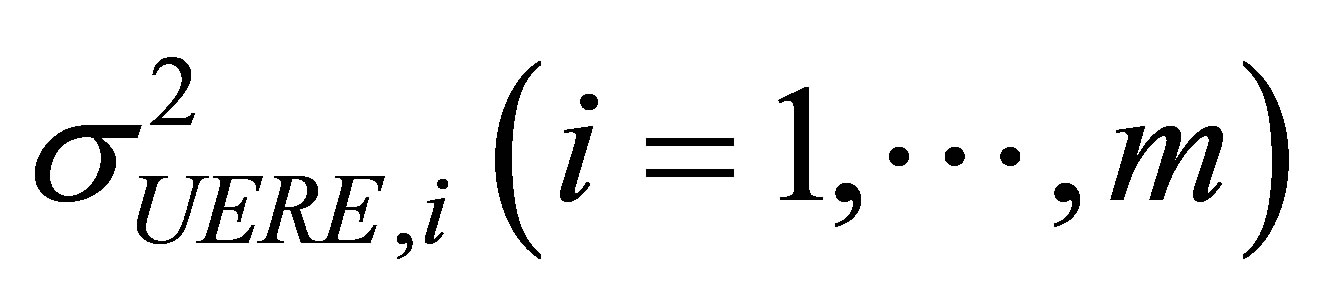 of each satellite forms the following diagonal matrix
of each satellite forms the following diagonal matrix 
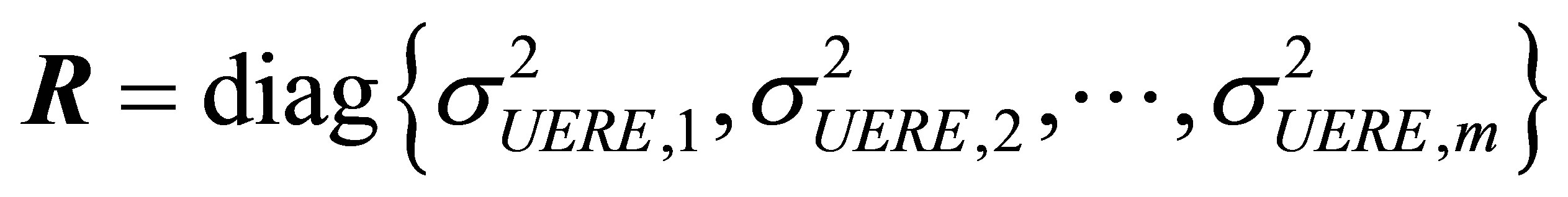 , (4)
, (4)
which contains the pseudo-range covariances, reflecting the uncertainty in the pseudo-range measurements. By taking  as the basic pseudo-range error, we convert the weight matrix into
as the basic pseudo-range error, we convert the weight matrix into
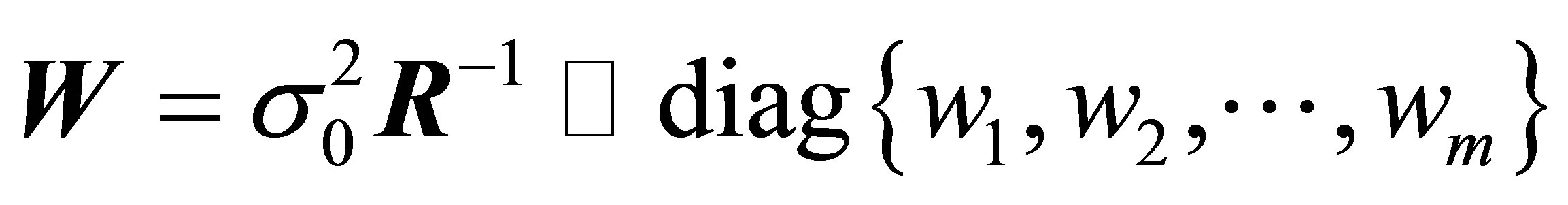 , (5)
, (5)
where “![]() ” means “denotes”. According to the property of diagonal matrices, we have
” means “denotes”. According to the property of diagonal matrices, we have
 , (6)
, (6)
and the size of the matrix  depends on the number of the visible satellites and it varies with time. The selection of
depends on the number of the visible satellites and it varies with time. The selection of  is only used for the normalization of
is only used for the normalization of 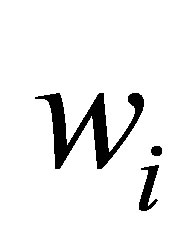 and can refer to the pseudo-range error of any type of the satellites in the mixed constellation. Take
and can refer to the pseudo-range error of any type of the satellites in the mixed constellation. Take ,
, 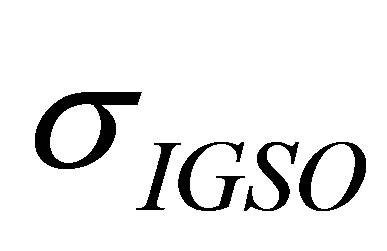 and
and 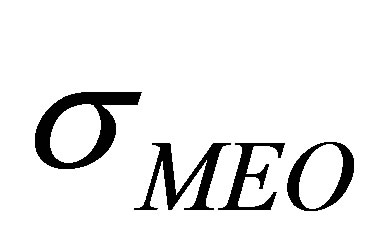 as the UERE values of the satellite types, respecttively. In this paper, we assume
as the UERE values of the satellite types, respecttively. In this paper, we assume . Then
. Then  influences the weight matrix and eventually the WDOP. By organizing the diagonal elements in the order of
influences the weight matrix and eventually the WDOP. By organizing the diagonal elements in the order of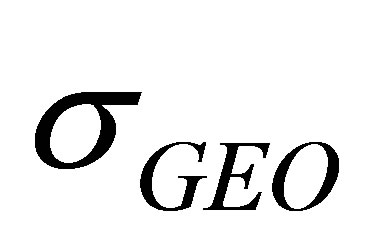 ,
, 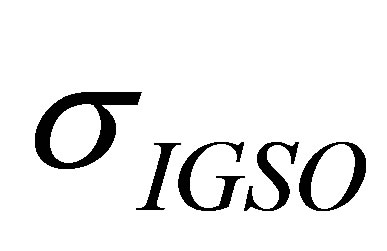 and
and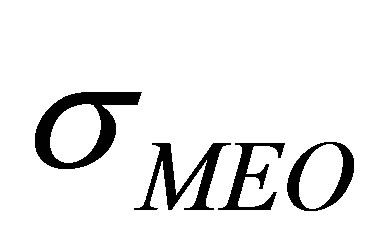 , we have
, we have
 . (7)
. (7)
In the rest of our analysis, we assume that: 1) The total numbers of satellites in the constellation are ,
,  (fixed), and with the stepwise deployment of the constellation, the number
(fixed), and with the stepwise deployment of the constellation, the number 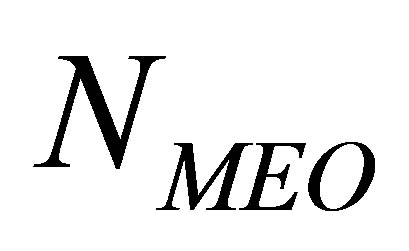 of MEO satellites is increasing. The constellation consists of
of MEO satellites is increasing. The constellation consists of  in-orbit satellites, where
in-orbit satellites, where ; 2) The UEREs for same type satellites have equal values, and
; 2) The UEREs for same type satellites have equal values, and ,
, 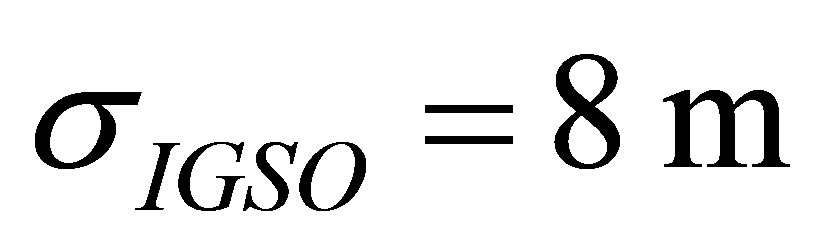 (fixed), while the value of
(fixed), while the value of  decreases gradually with the improvements of hardware and software techniques.
decreases gradually with the improvements of hardware and software techniques.
Therefore, we can regard the WDOP at a certain instant as a two-variable function, with  as the function forms, that is
as the function forms, that is
 (8)
(8)
In the following we discuss respectively the influences of 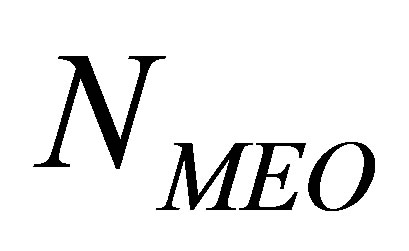 and
and 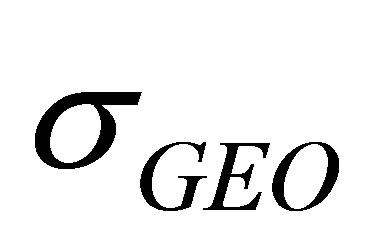 on the WDOP to illustrate the changes in positioning precision during the constellation stepwise deployment. For convenience, we denote the joint influence as
on the WDOP to illustrate the changes in positioning precision during the constellation stepwise deployment. For convenience, we denote the joint influence as .
.
3. Positioning Precision as Influenced by Selection of Parameters
3.1. Relationship between Number of MEO Satellites and WDOP
In this section, we fix 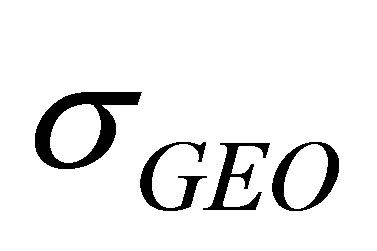 and study the impact of
and study the impact of  on the WDOP. By taking
on the WDOP. By taking  as a set of
as a set of 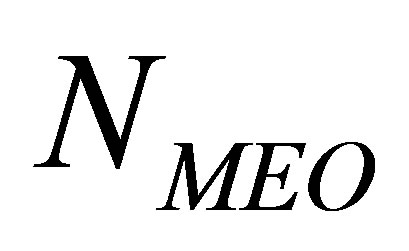 MEO satellites in the constellation, we have the following proposition.
MEO satellites in the constellation, we have the following proposition.
Proposition I At any fixed instant,  is monotonically non-increasing with
is monotonically non-increasing with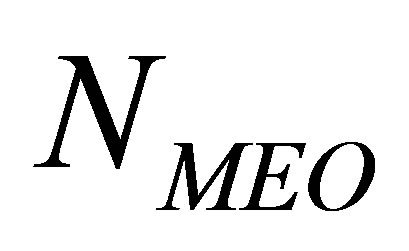 . That is, for any
. That is, for any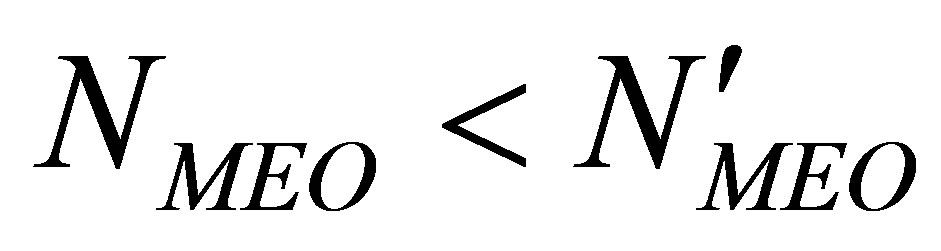 , and
, and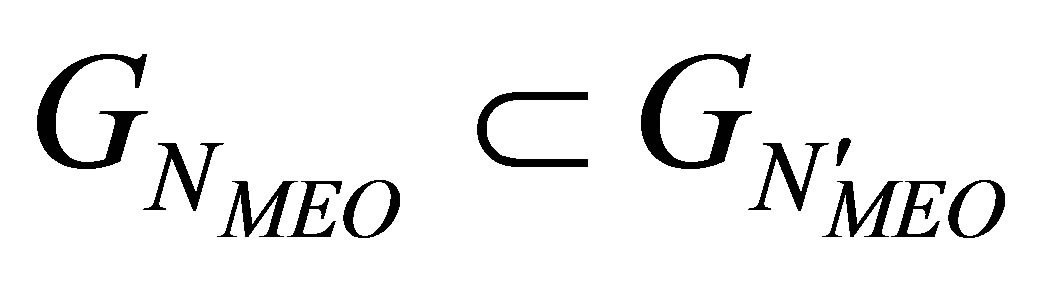 , the following holds true:
, the following holds true:
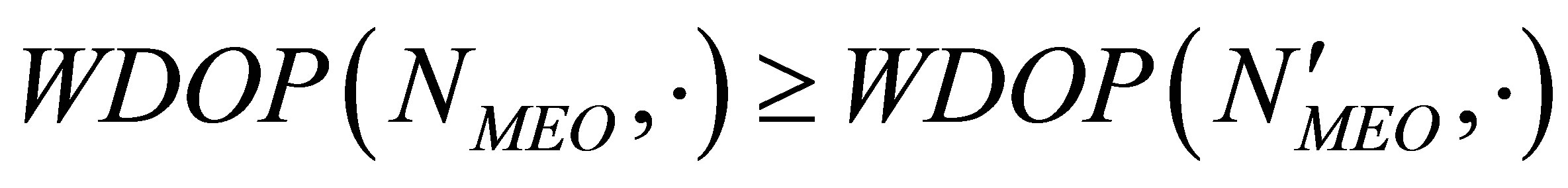 . (9)
. (9)
Proof If we can prove that the WDOP value decreases or remains the same while an MEO satellite is added to the set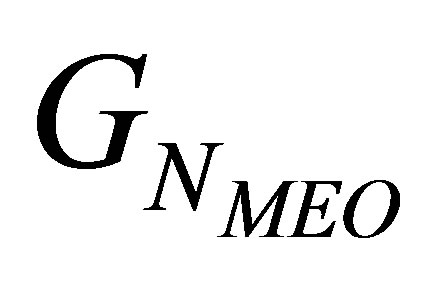 , i.e.,
, i.e.,
 , (10)
, (10)
then we can get recursively that

To prove Equation (10), let us consider two cases.
1) When the added MEO satellite is not visible to the user, i.e.,  , then the increase of
, then the increase of 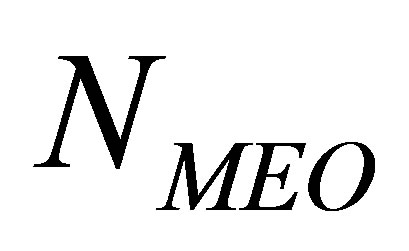 does not change the total number m of visible satellites, the corresponding design matrix
does not change the total number m of visible satellites, the corresponding design matrix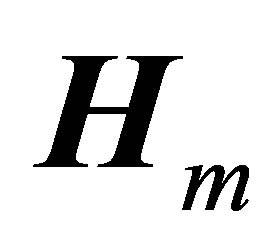 , and the weight matrix
, and the weight matrix . Thus we have
. Thus we have
 . (11)
. (11)
2) When the added MEO satellite is visible to the user, then the total number of visible satellites increases from 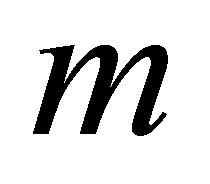 to
to . From the fact that the weight matrix
. From the fact that the weight matrix  is diagonal and satisfies Equation (5), we have
is diagonal and satisfies Equation (5), we have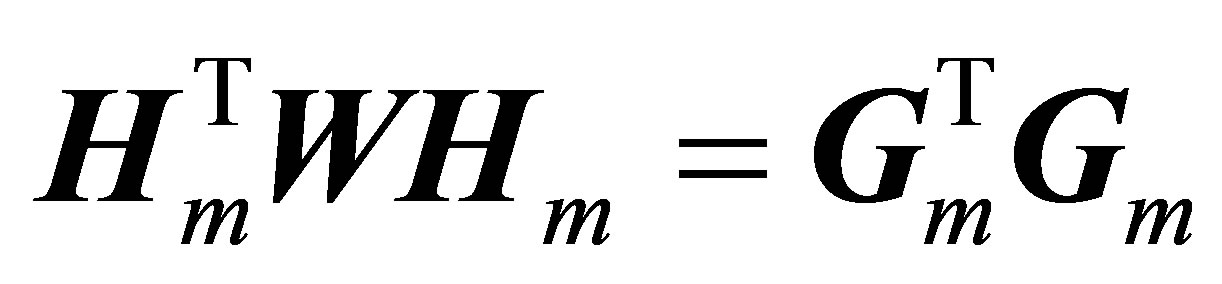 , where
, where
 .
.
Therefore the following relation is true:
 , (12)
, (12)
where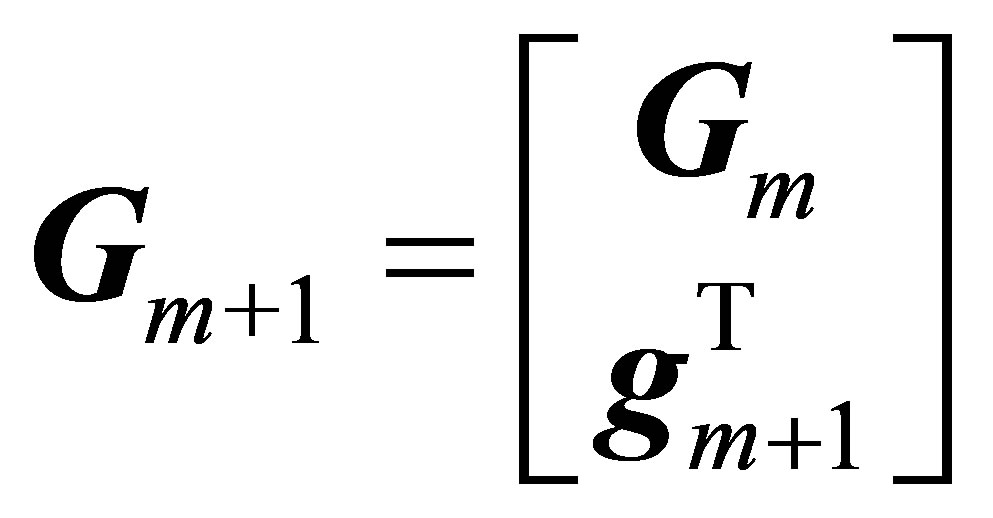 ,
,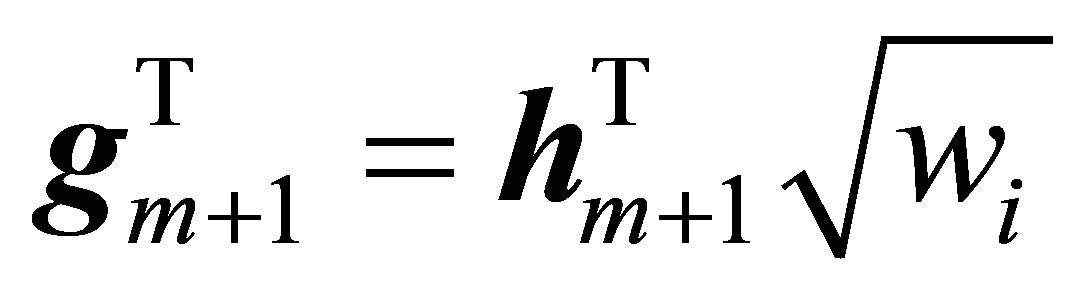 .
.
The following part of the proof is the same as given in [10]. To make the proof complete, it is summarized as follows.
Performing the singular value decomposition on  produces
produces
 , (13)
, (13)
where 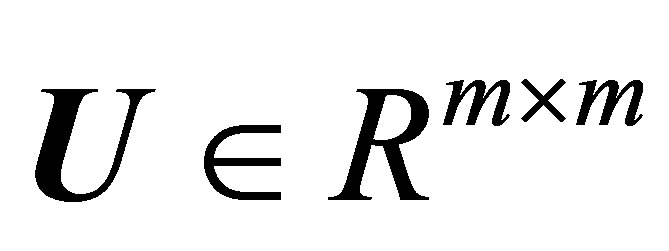 and
and  are orthogonal matrices, and
are orthogonal matrices, and  a diagonal matrix.
a diagonal matrix.
By substituting Equation (13) into Equation (12), and making the same orthogonal transformation to both sides of the resultant equation, we get the following set of equations based on the fact that an orthogonal transformation does not change the trace of a matrix:
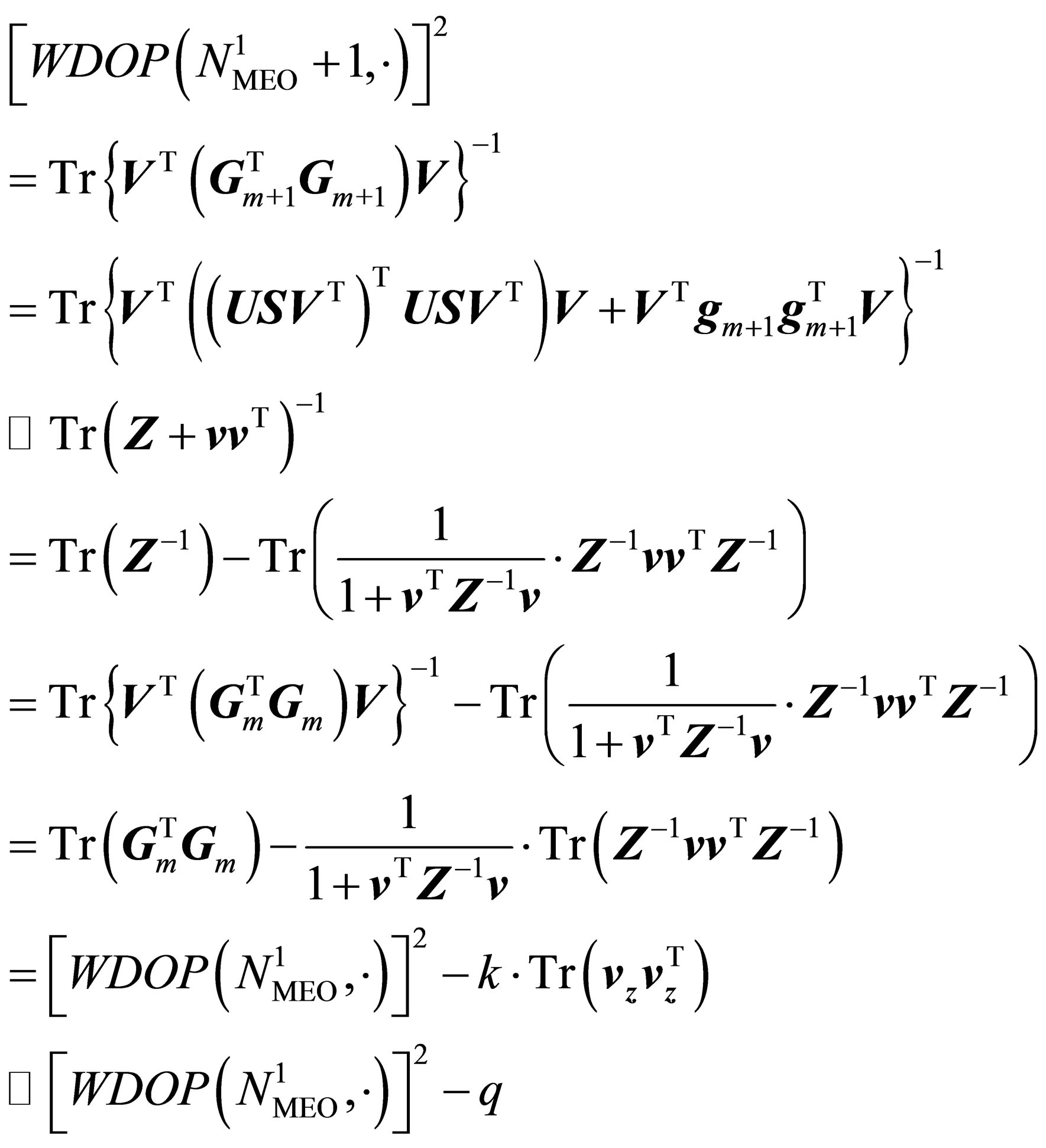
where
 ,
,
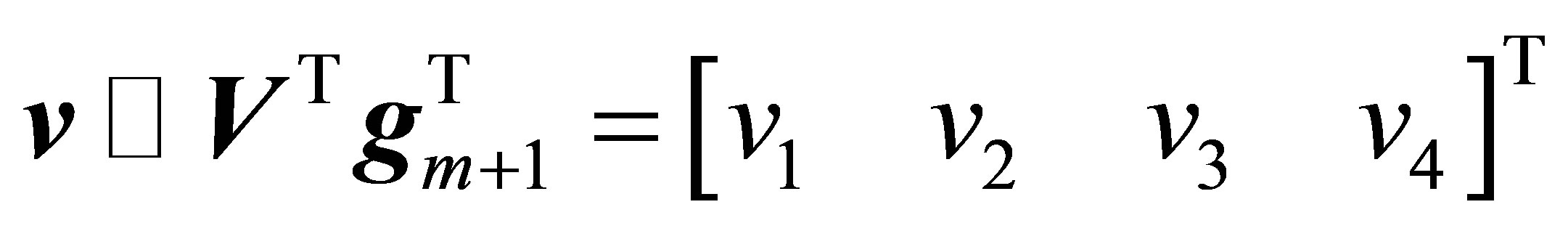 ,
,
 ,
,  and
and
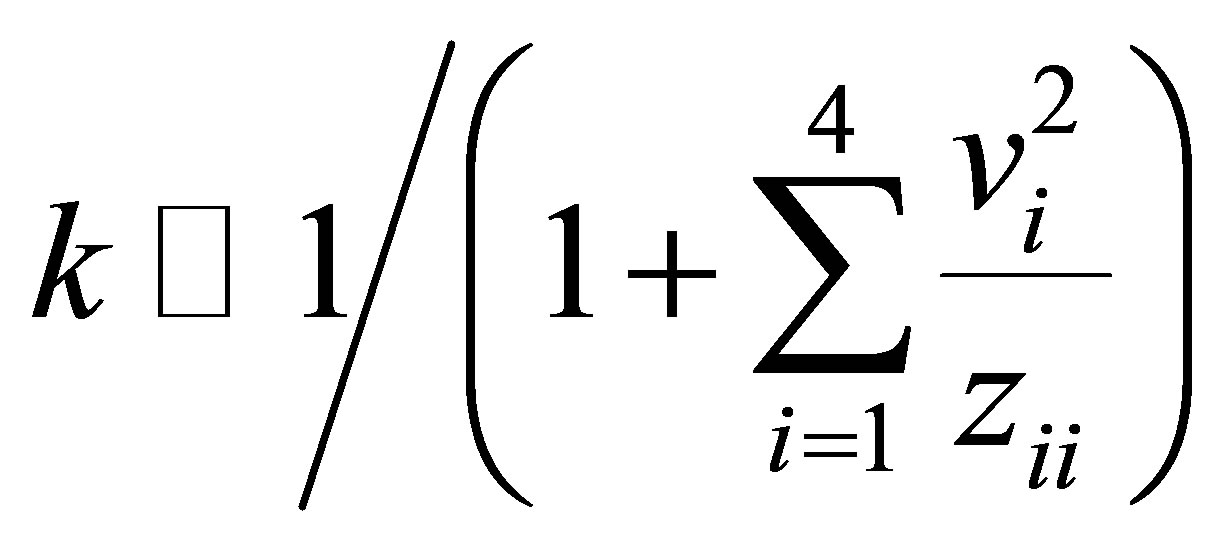 thus
thus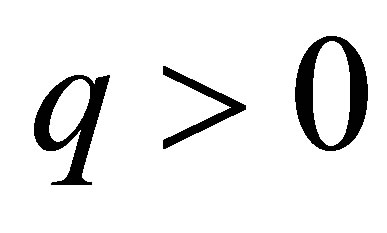 . Therefore, we have
. Therefore, we have
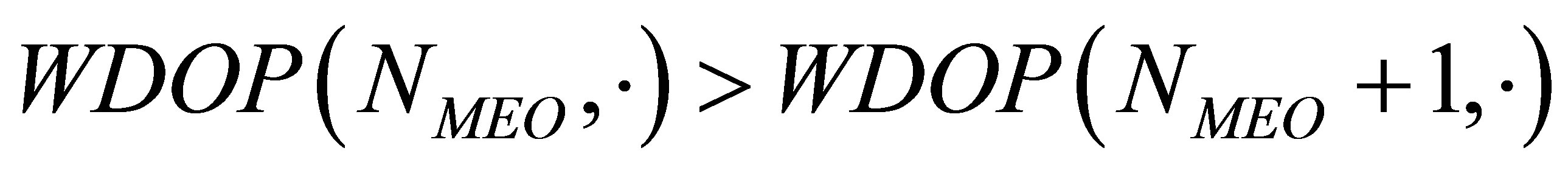 . (14)
. (14)
By Integrating Equation (11) and Equation (14), we get Equation (10). This concludes the proof of the proposition.
Remark: The contribution of a new satellite to the WDOP value can also be calculated. That is, from Equation (12) and the Sherman-Morrison formula the following holds true:
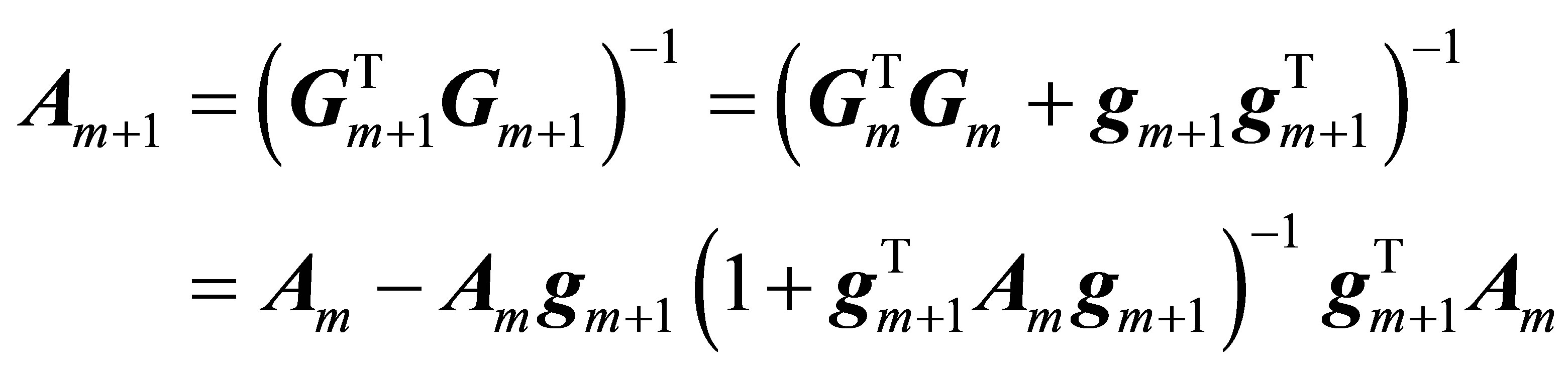
where  is a scalar. So we have
is a scalar. So we have
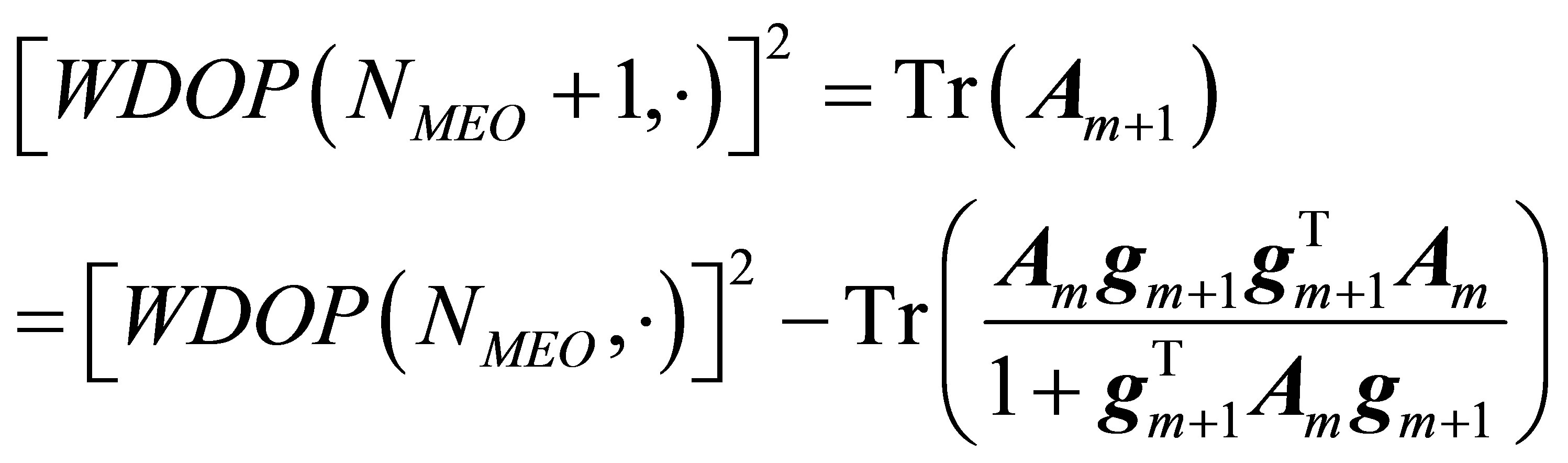
Now, it can be readily seen that
 . (15)
. (15)
These formulas jointly produce the recursive algorithm from 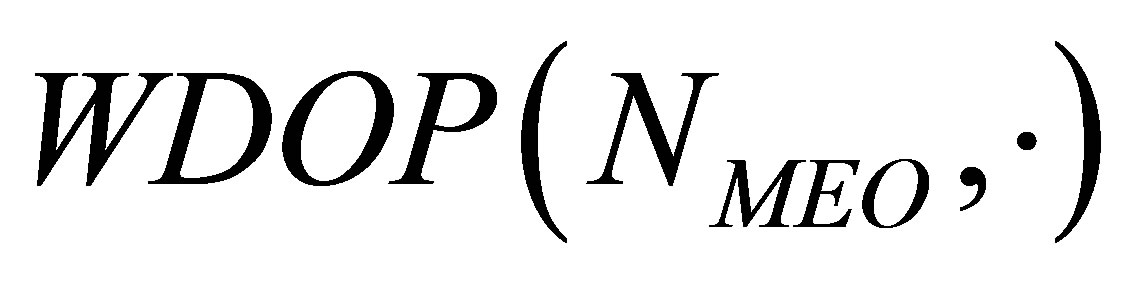 to
to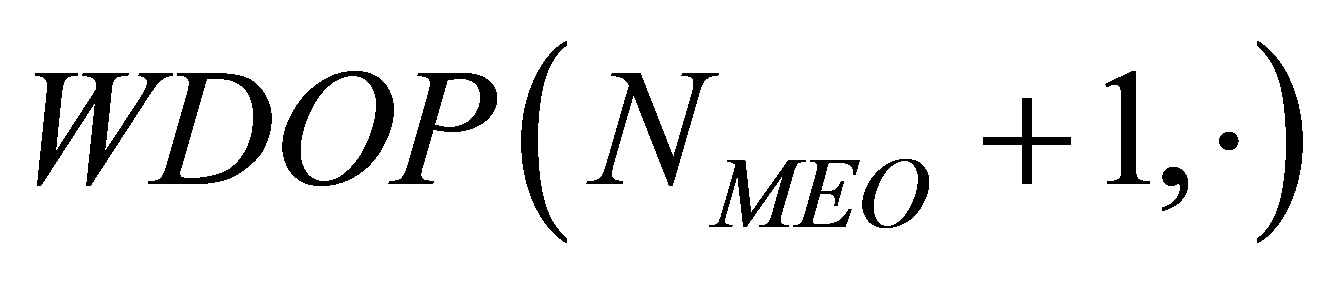 ; and the magnitude of
; and the magnitude of 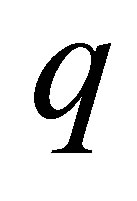 shows the decrement in WDOP as produced by adding a new MEO satellite visible to the user. The recursion lowers the storage loads due to savings in computation incurred in the reduced matrix inversion and repetitious operations.
shows the decrement in WDOP as produced by adding a new MEO satellite visible to the user. The recursion lowers the storage loads due to savings in computation incurred in the reduced matrix inversion and repetitious operations.
3.2. Relationship between GEO Satellites UERE and WDOP
In this section, with 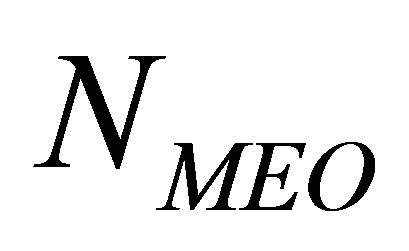 fixed we look at the impact of
fixed we look at the impact of 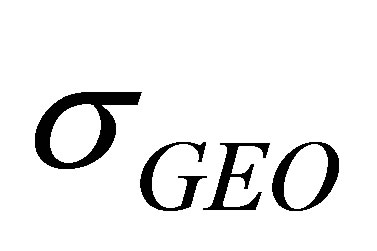 on WDOP.
on WDOP.
Proposition II At any chosen instant, 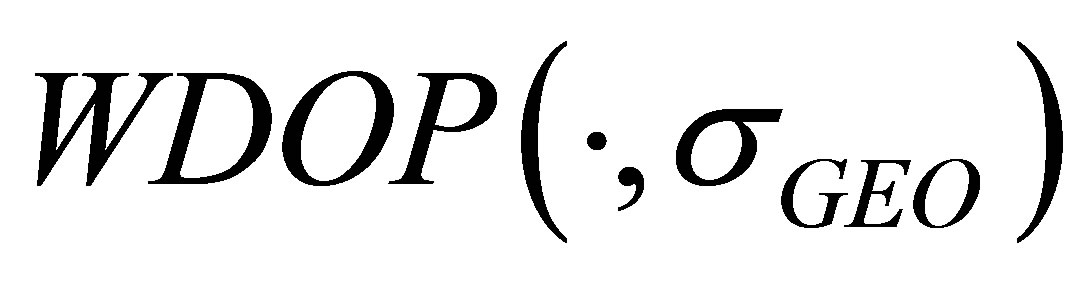 is monotonically non-increasing as
is monotonically non-increasing as 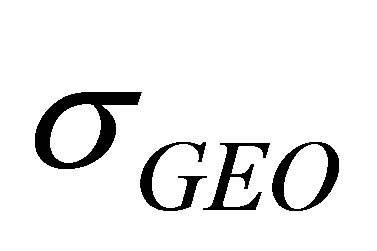 decreases. That is, for any
decreases. That is, for any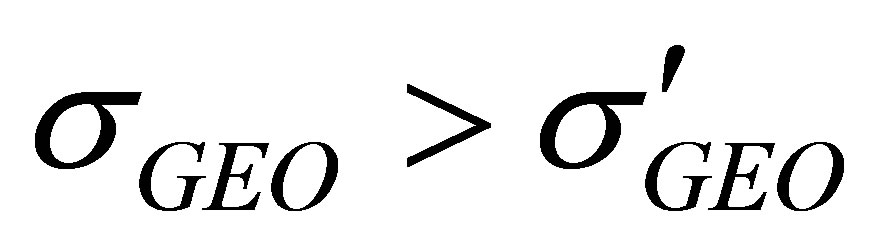 , the following holds:
, the following holds:
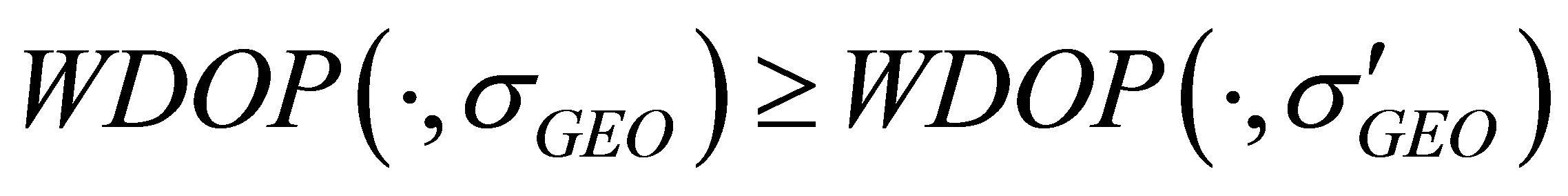 . (16)
. (16)
Proof Generally, let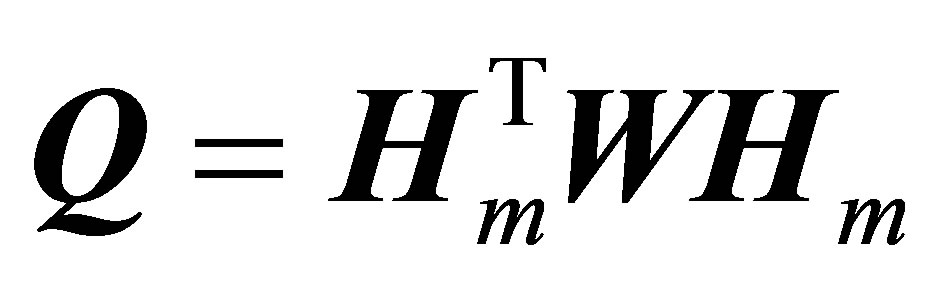 . Then
. Then  is a 4th order square matrix for any
is a 4th order square matrix for any ![]() value.
value.
Because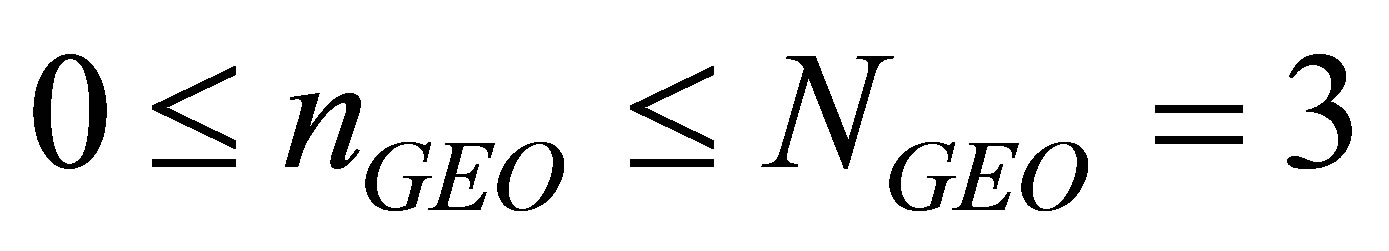 , if
, if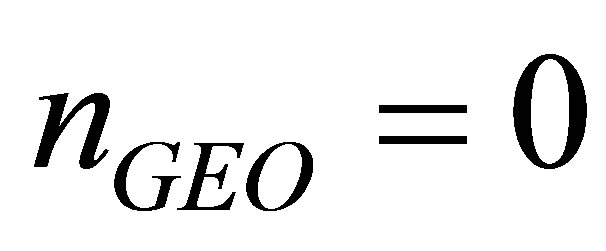 , i.e., there is no GEO satellite among the satellites visible to the user, then the change of
, i.e., there is no GEO satellite among the satellites visible to the user, then the change of 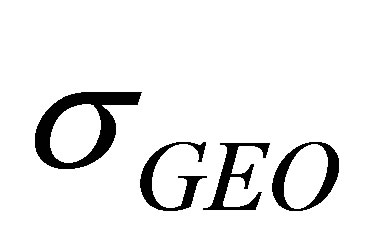 does not make any difference in the matrix
does not make any difference in the matrix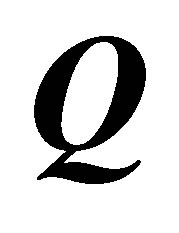 . Hence we have
. Hence we have
 .
.
In the following, we focus on the proof for the circumstances that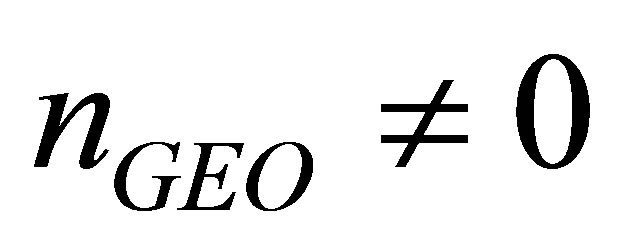 . For any
. For any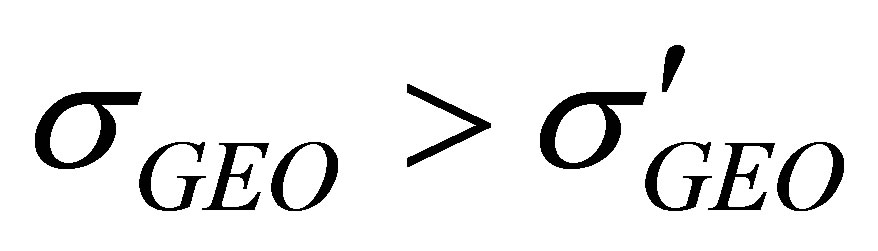 , there is
, there is 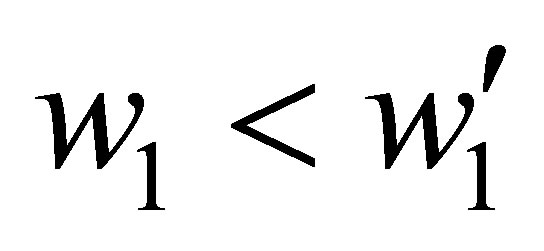 such that one of the following three cases occurs.
such that one of the following three cases occurs.
1) Assume that 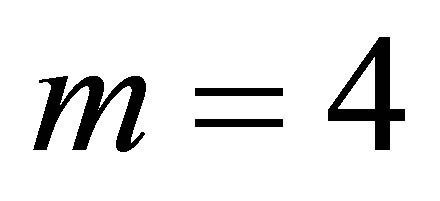 and
and . Then
. Then . Now
. Now  is a 4th order inversible square matrix. Hence we have
is a 4th order inversible square matrix. Hence we have
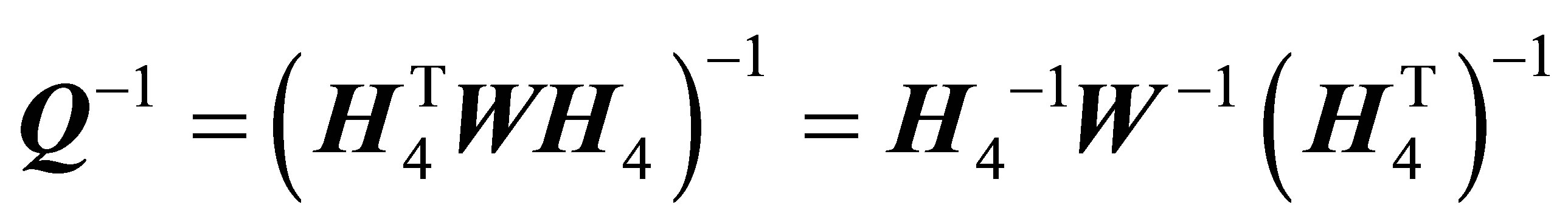 .
.
Let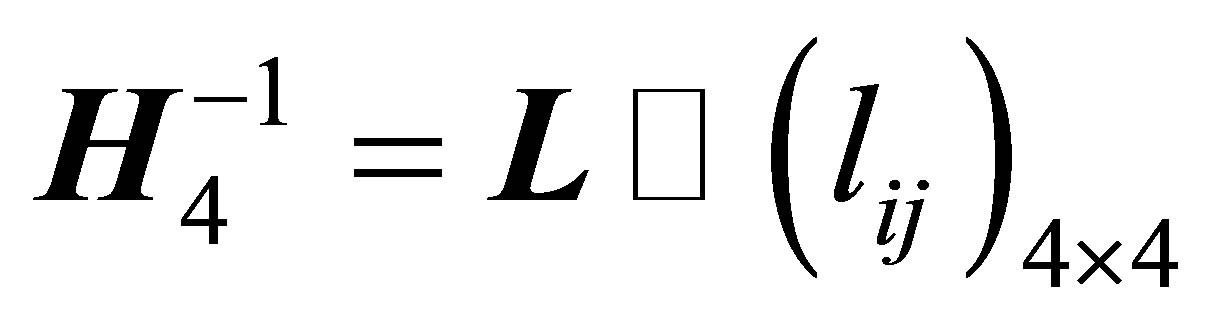 . Then from
. Then from
 it follows that
it follows that
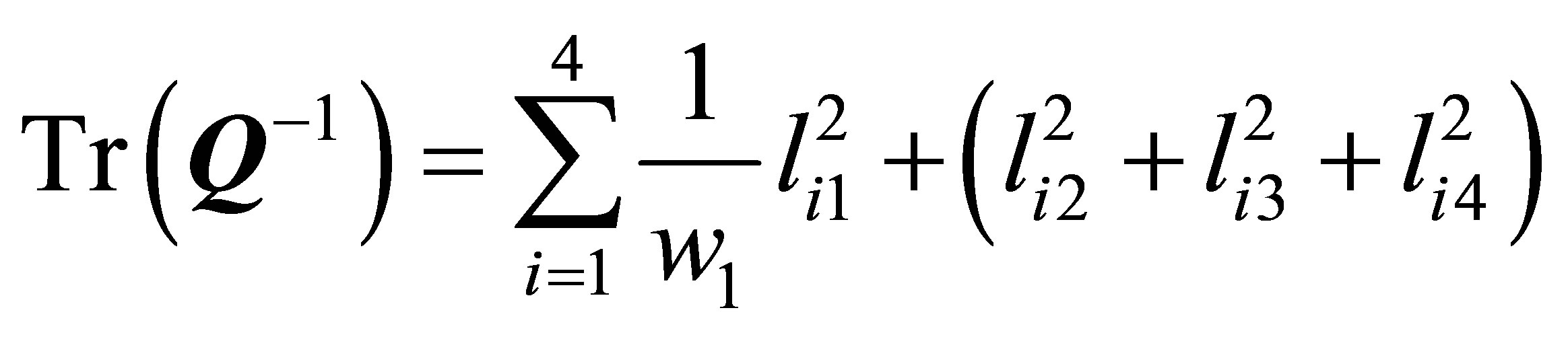 .
.
Therefore, from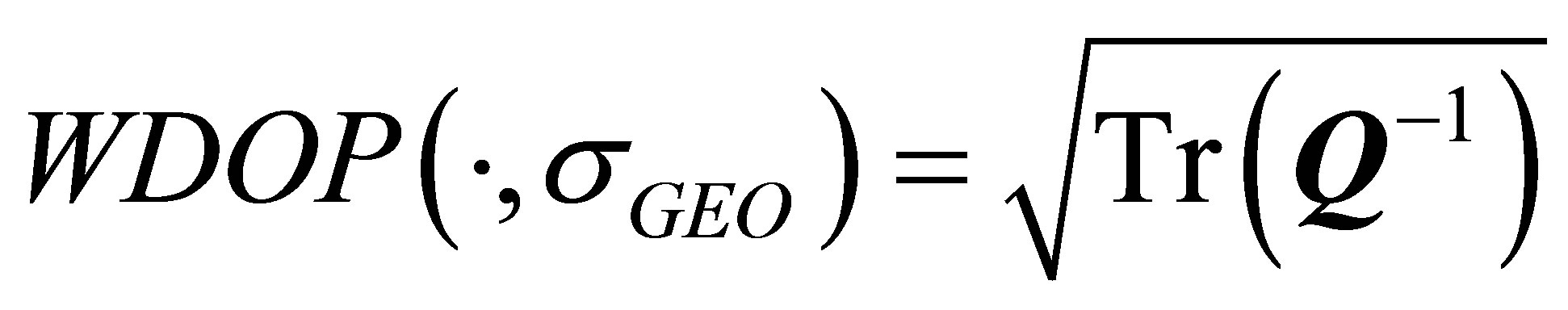 , it follows immediately that
, it follows immediately that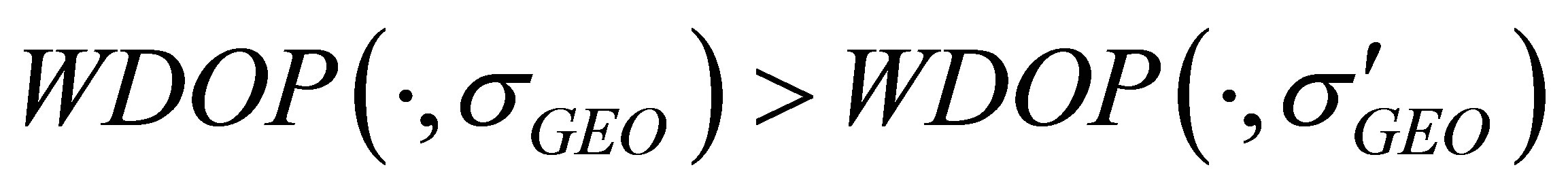 .
.
2) Suppose that a GEO satellite is added on the basis of case 1), so that  and
and . Then
. Then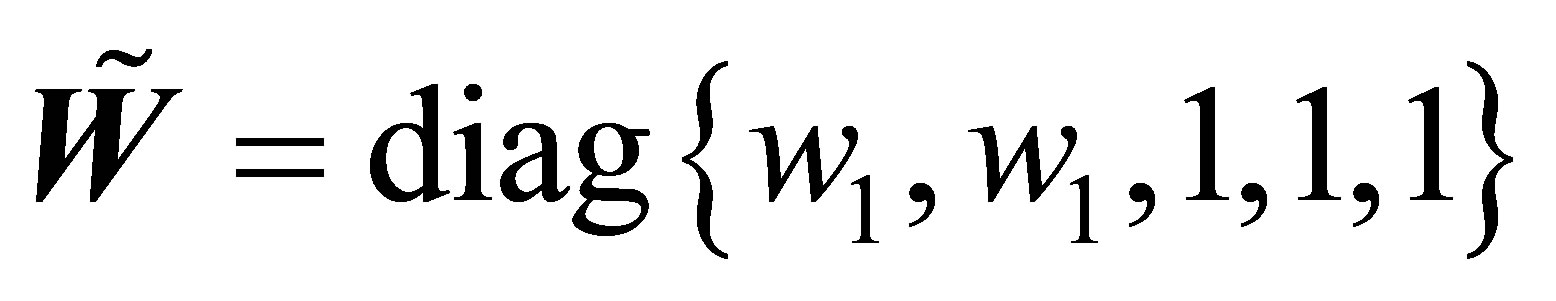 . Now because
. Now because  is not square, the method above cannot be applied. Let us consider the block matrix:
is not square, the method above cannot be applied. Let us consider the block matrix:
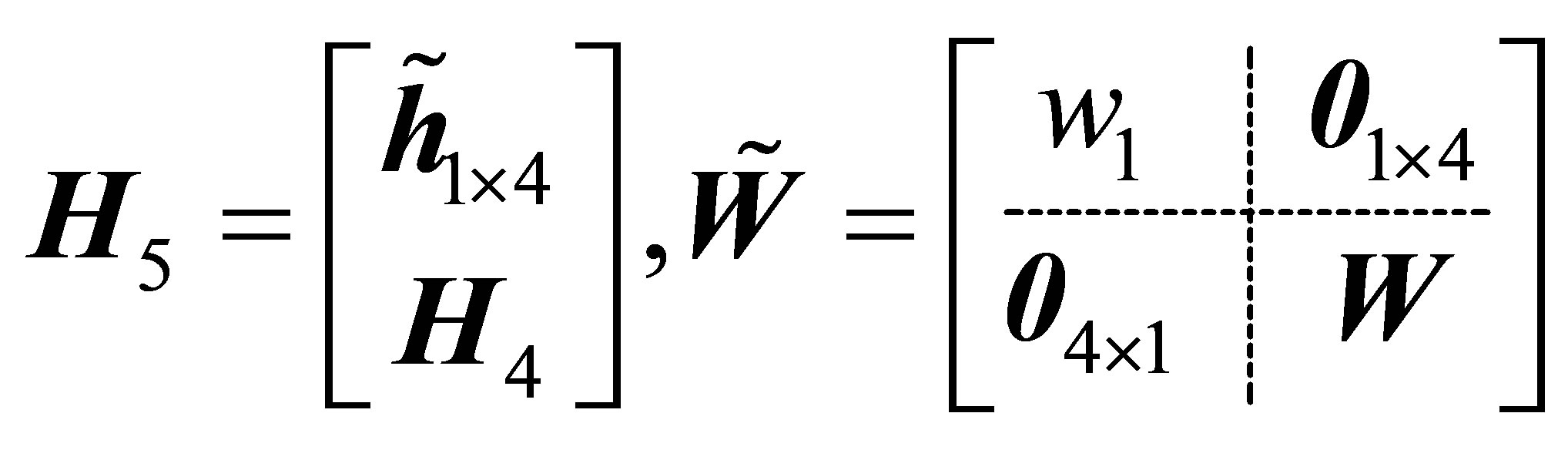 .
.
So we have
 .
.
By the Sherman-Morrison formula we have
 therefore
therefore
 (17)
(17)
Because 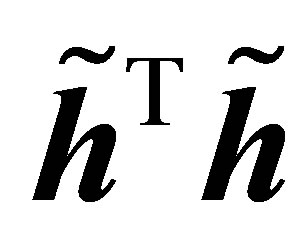 is a non-negative definite matrix with eigenvalues 0, 0, 0, and 2, and
is a non-negative definite matrix with eigenvalues 0, 0, 0, and 2, and 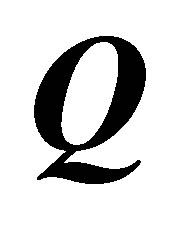 is a positive definite matrix,
is a positive definite matrix, 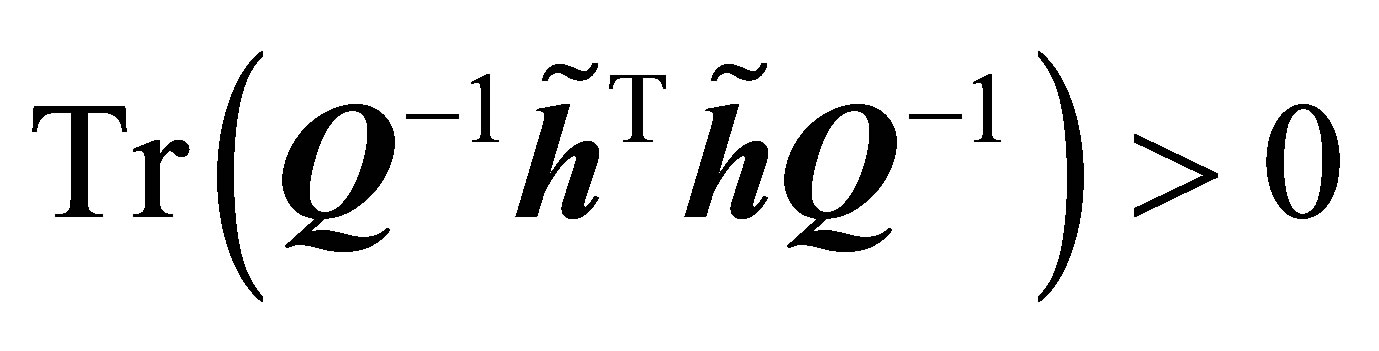 , and
, and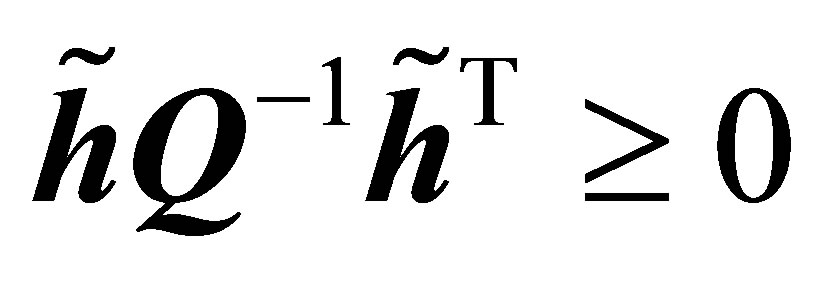 . Hencefor
. Hencefor ,
,  holds true. From case 1) we have
holds true. From case 1) we have
 , i.e.,
, i.e., 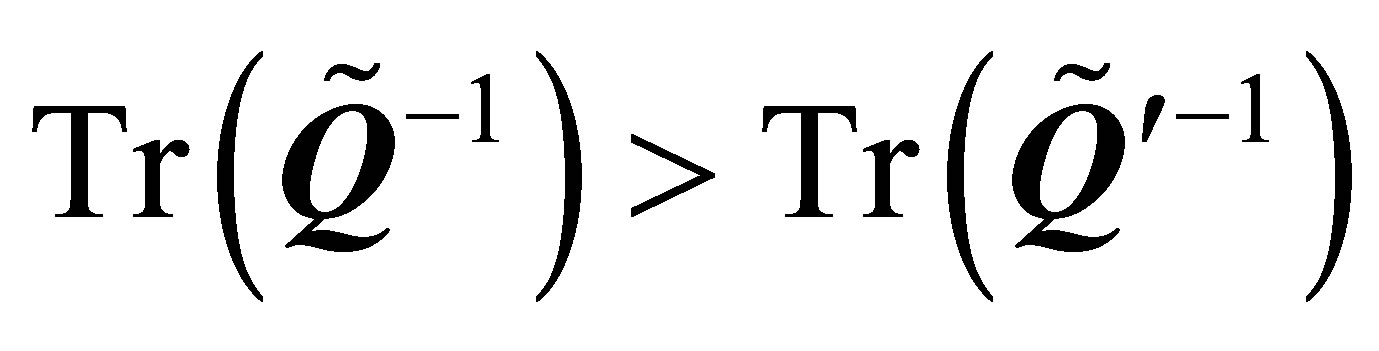 , so
, so
 .
.
3) Suppose that either an IGSO or a MEO satellite is added on the basis of case 1), so that  and
and
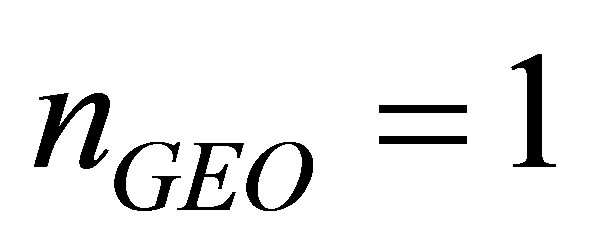 . Then
. Then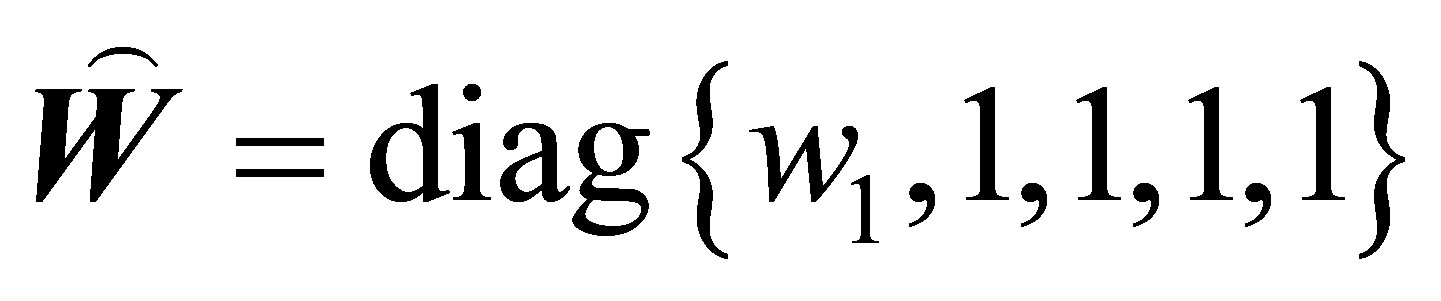 . Let
. Let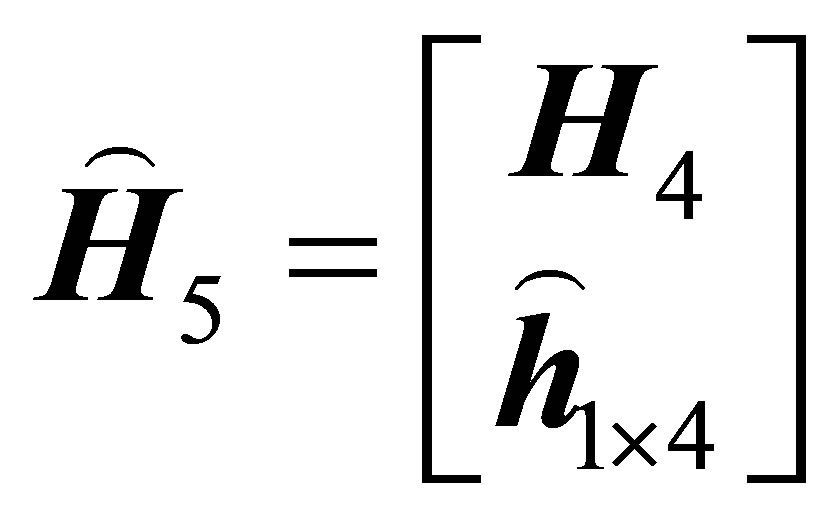 .
.
Then we can prove in a similar way as in case 2) that according to Equation (17), we have
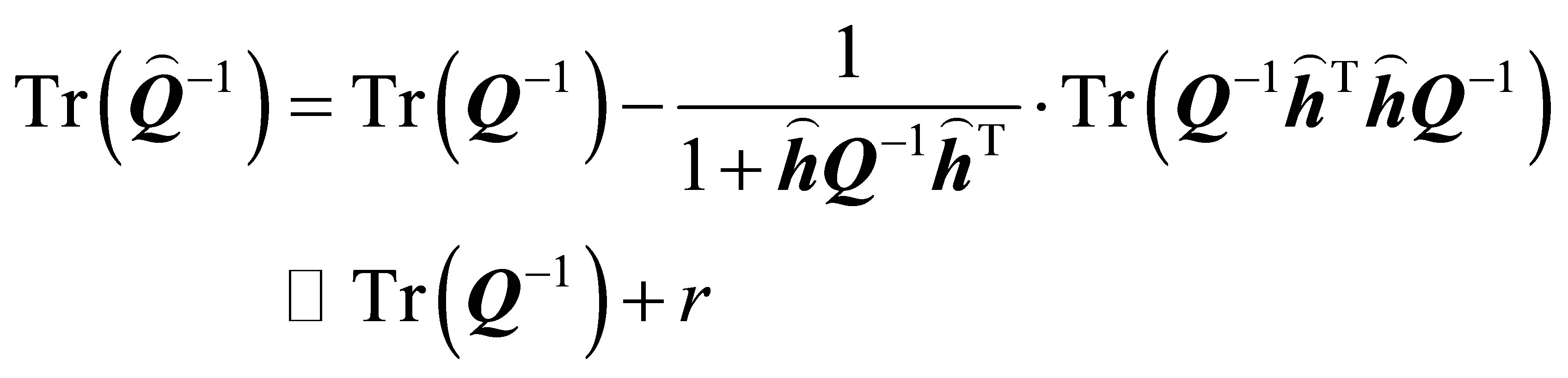 (18)
(18)
where  is irrelevant to
is irrelevant to . Therefore,
. Therefore,
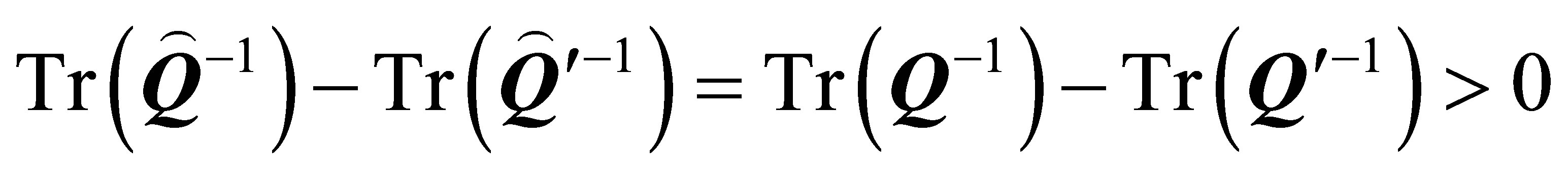 which leads to
which leads to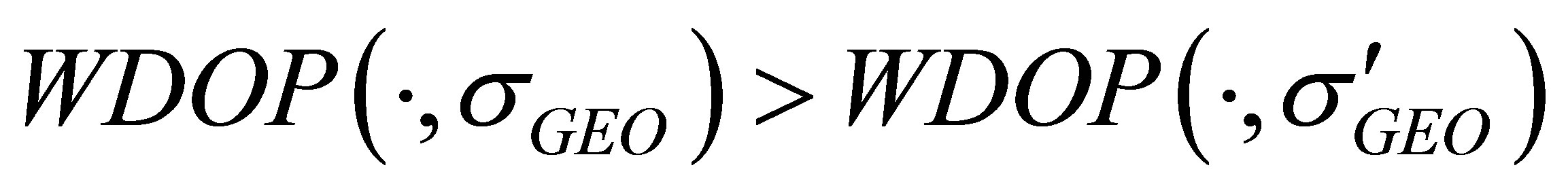 .
.
We can repeat the steps above recursively and eventually lead to the conclusion that for any
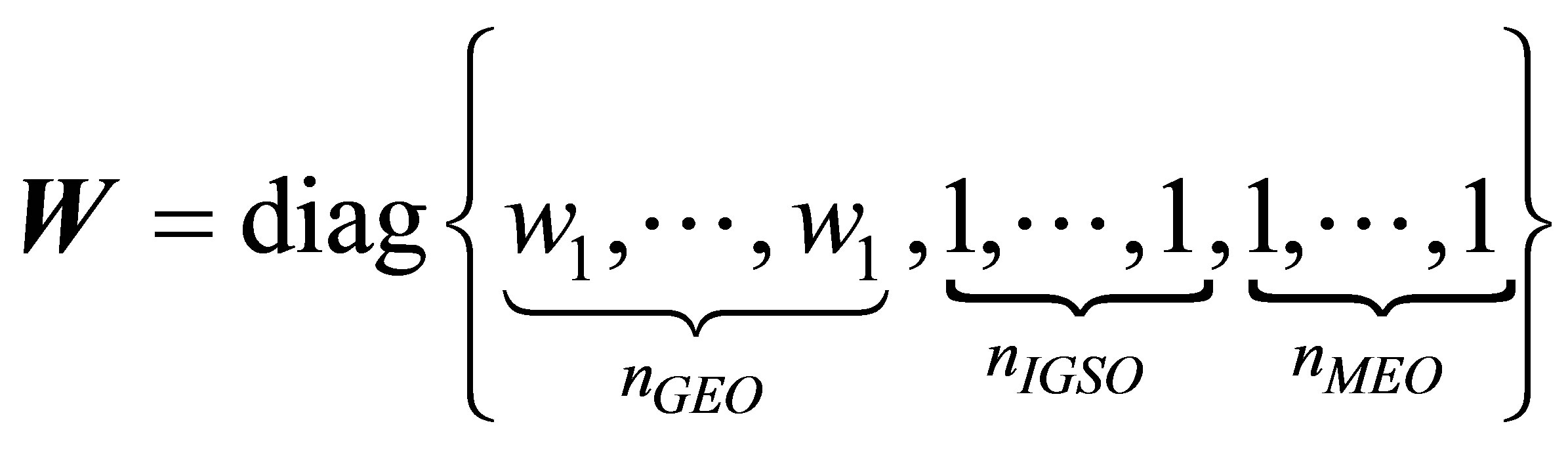 Equation (16) holds.
Equation (16) holds.
4. Positioning Precision Analysis and Simulating the Inversion of Parameters
Let us take 2012-01-01 00:00 UTCG as the initial epoch. The total duration for our simulation is one day. The following results show the mean values of the whole period. We generate the completed COMPASS constellation by the configuration of 3 IGSO + 3 GEO + 24 MEO satellites. The MEO satellites form a Walker 24/3/2 constellation with their stepwise deployment and eventually provides the global coverage. Assume that the semi-major axis is 27905.5 km. The GEO satellites are located along the longitudes of 80˚E, 110.5˚E, and 140˚E, respectively. The intersecting longitude of the IGSO satellites is 118˚E.
4.1. Positioning Precision Analysis for Different Constellation Deployment Scenarios
As the MEO satellites are launched in steps, there exists a variety of possible constellation deployment scenarios, each of which will affect the positioning performance of the system. We consider two different schemes as suggested in [4], and see how the characteristics of the positioning precision evolve with varying parameters. In the following, S12 denotes the second satellite on the first orbital plane, and the same notation rule applies for the other satellites.
Scheme I:
S11 → S12 → S13 → S14 → S15 → S16 → S17 → S18 → S21 → S22 → S23 → S24 → S25 → S26 → S27 → S28 → S31 → S32 → S33 → S34 → S35 → S36 → S37 → S38;
Scheme II:
S26 → S13 → S22 → S17 → S28 → S24 → S37 → S33 → S23 → S27 → S32 → S36 → S25 → S31 → S35 → S38 → S34 → S21 → S18 → S16 → S12 → S15 → S11 → S14.
Let us take the Beijing COMPASS station as an example of the users. The relationship between the number of MEO satellites, the UERE of GEO satellites, and the WDOP values under these two schemes are shown in Figure 1, in which the contour maps of WDOP are presented as a function of these two factors.
Several phenomena can be seen out of the simulation results. 1) WDOP decreases with the increase of MEO satellites numbers or with the decrease of GEO satellites UERE. This is consistent with the results of theoretical derivation; 2) the number of satellites poses a greater impact on the decrease of WDOP, while the extent of the decrement declines with the increase of the number. More specifically, the launch of each additional satellite improves the positioning precision at the initial deployment of the constellation, while little improvement can be seen in the WDOP after the number of MEO satellites
 (a)
(a)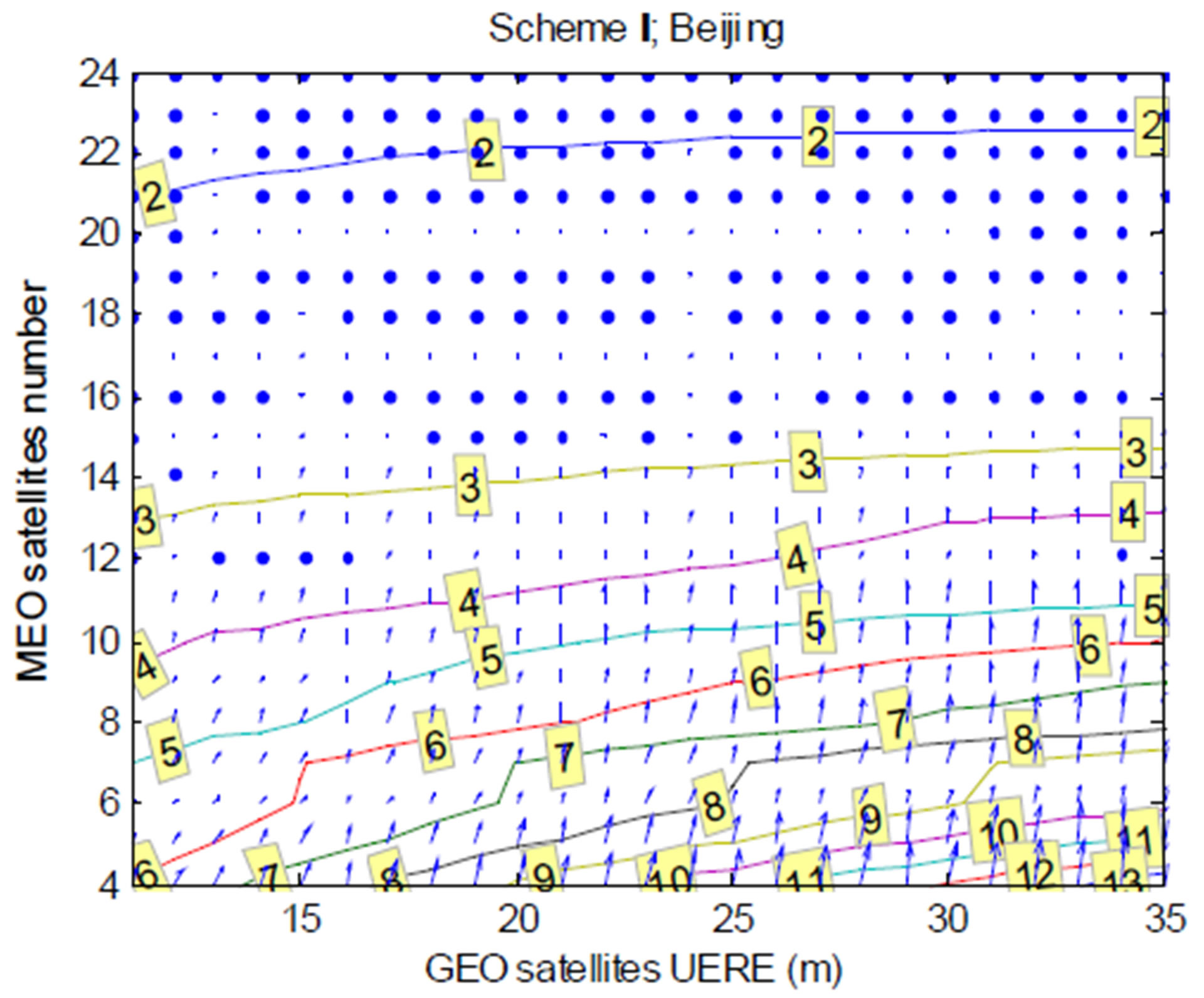 (b)
(b)
Figure 1. The relationship between MEO satellites number, GEO satellites UERE and WDOP values. (a) WDOP contour map (constellation scheme I; Beijing station); (b) WDOP contour map (constellation scheme II; Beijing station).
reaches a certain level, such as 12 or so. In such circumstances, enhancement in the positioning precision becomes limited; and 3) even if the numbers of satellites in orbit are the same, different constellation configurations affect the evolutionary pattern of the WDOP values during the process of deployment. Therefore, it is essential to consider relevant factors jointly in all aspects in order to design the optimal constellation deployment.
4.2. Positioning Precision Analysis for Different User Types
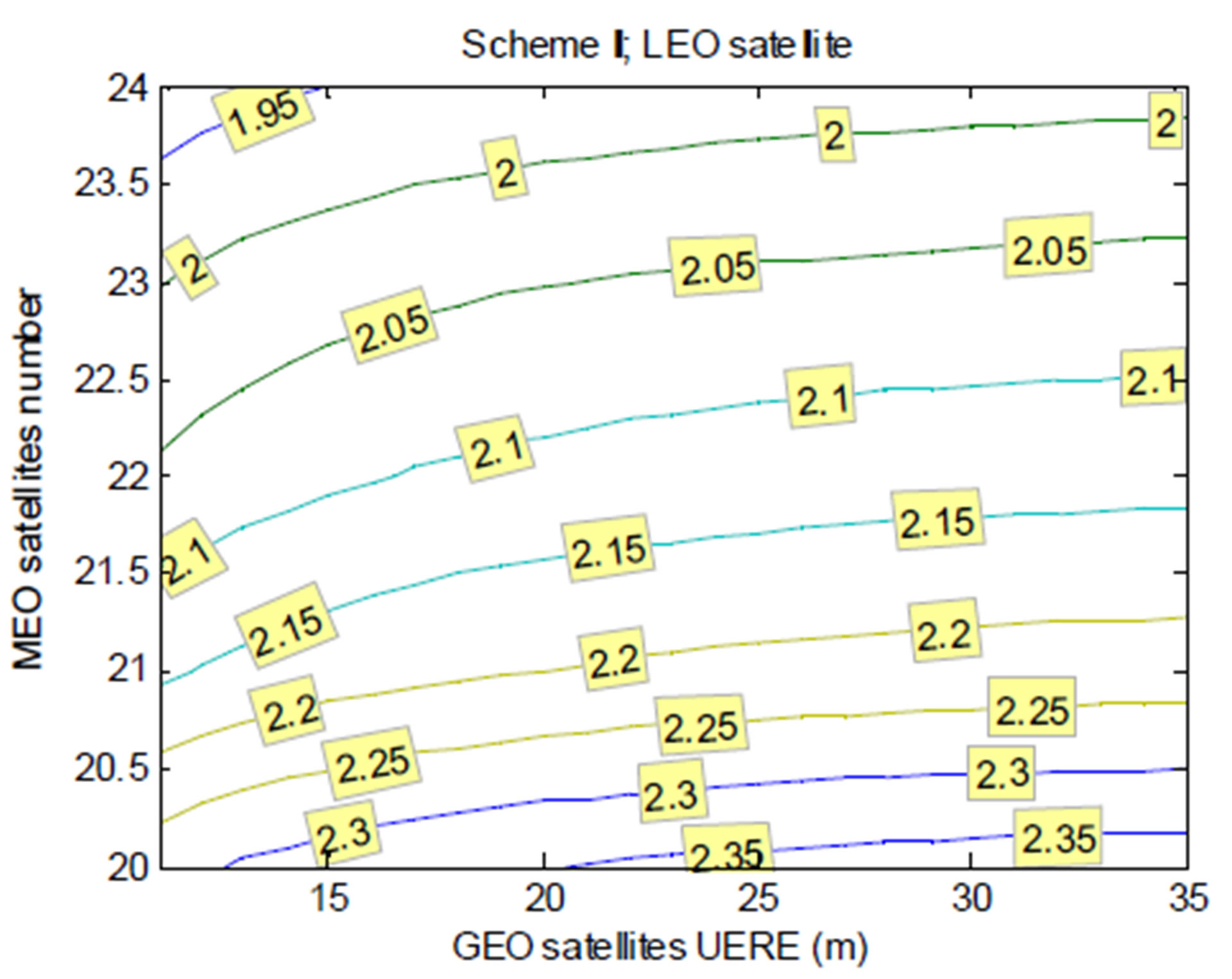
Since future potential users will not be limited to the ground-based ones, let us also analyze the positioning performance for a low Earth orbit (LEO) satellite based on the COMPASS system. Assume that the orbital elements of the LEO satellite are: semi-major axis is 6678 km, eccentricity 0, inclination 28.5˚, perigee 0˚, ascending node right ascension 0˚, mean anomaly 0˚. Computer simulation shows that under the constellation Scheme I, at least 22 MEO satellites are needed to make the LEO satellite positioning possible at any time; and under Scheme II, at least 20 MEO satellites are required. The reason is that the LEO satellite moves around the Earth in space, thus the regionally augmented function of GEO and IGSO satellites is weakened and the receiver onboard of the LEO satellite relies most of the time on the visibility of the MEO satellites.
Figure 2(a) shows the evolutionary pattern of the WDOP for the LEO satellite by using Scheme II of the stepwise deployment. In particular, due to the satisfactory viewing geometry between the satellites in the constellation and the LEO satellite, the WDOP values are relatively small, and the number of MEO satellites plays a leading role in increasing the magnitude of the WDOP. Figure 2(b) illustrates the variation curves of the WDOP as a function of the GEO satellites UERE with different numbers of MEO satellites. It can be seen that in order to improve the positioning precision, the focus should be on the completion of launching the MEO satellites in the constellation, because the LEO satellite moves at a relatively high speed to the constellation. Consequently, the key to improve the positioning geometry is to enhance the constellation coverage.
4.3. Inversion of Parameters under the Desired Positioning Precision
From the perspective of both theory and simulation, we have analyzed the influence of selected parameters, namely, the number and the UERE of satellites, on the magnitude of the WDOP. The significance of this analysis can be illustrated better in the following sense: The requirements of the system’s parameters can be proposed in the reversed direction for any specified WDOP standard,
 (a)
(a) (b)
(b)
Figure 2. WDOP simulation results for the LEO satellite. (a) WDOP contour evolution; (b) WDOP vs. GEO satellites UERE (for different numbers of MEO satellites).
which is often a measure of the positioning precision of the constellation. The inversion of parameters can be performed to provide a practical reference to the stepwise deployment strategy.
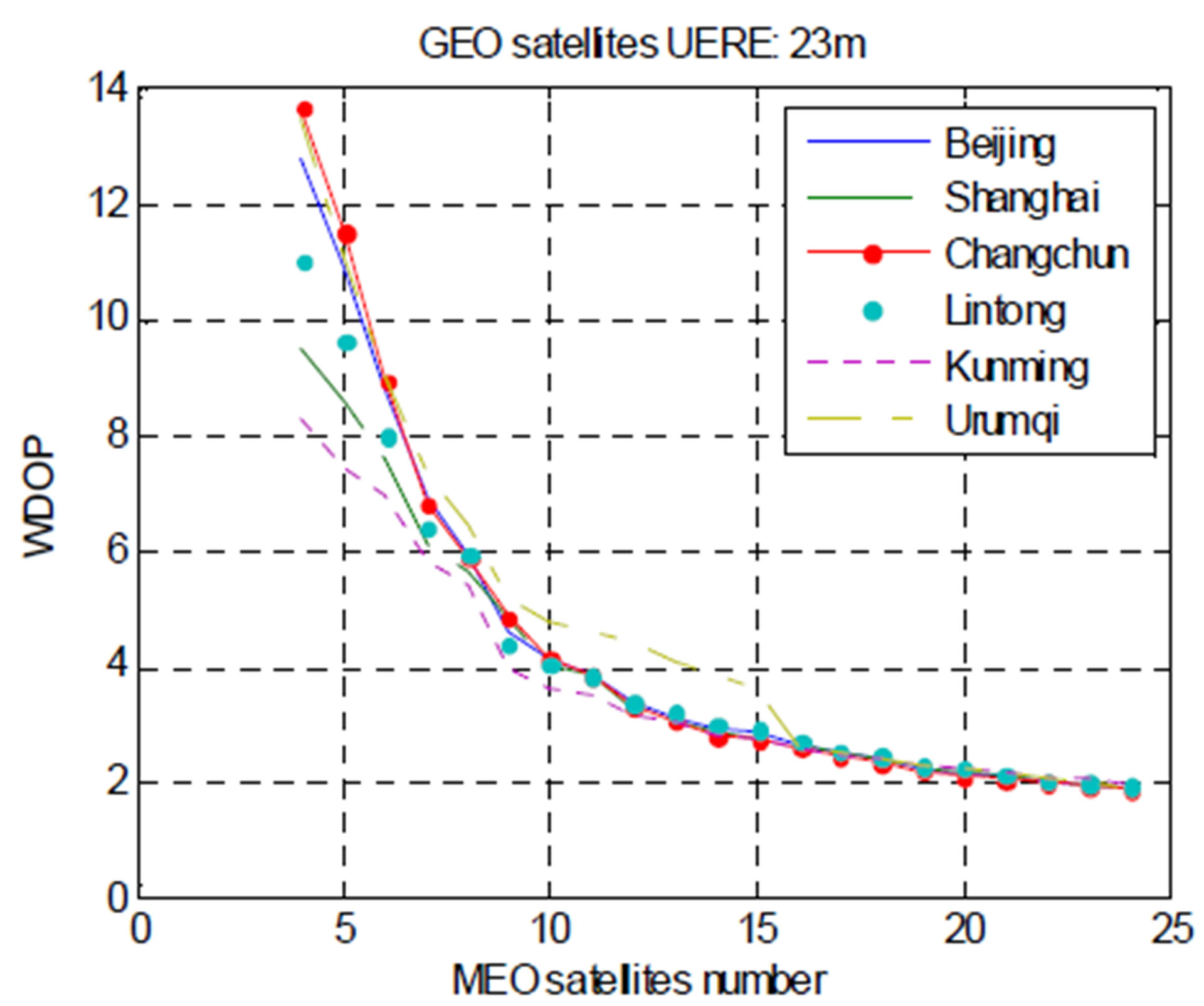
We select 6 ground stations in China: Beijing, Shanghai, Changchun, Lintong, Kunming, and Urumqi, and apply constellation Scheme I. Considering the two factors discussed above with one of the parameters fixed produces a profile of the WDOP for the other parameter, as Figure 3 shows.
Suppose that the requirement for positioning precision is given as WDOP ≤ 2.5. Then we can tell from Figure 3 that: 1) If the current level of GEO satellites UERE is 23 m, then in addition to the existing GEO and IGSO satellites, at least 18 MEO satellites are needed to meet the positioning precision for Beijing and Lintong stations, and at least 17 MEO satellites are needed for the remaining four stations; and 2) If the current constellation consists 16 MEO satellites besides the GEO and IGSO satellites, then the upper bounds of the GEO satellites UERE
 (a)
(a)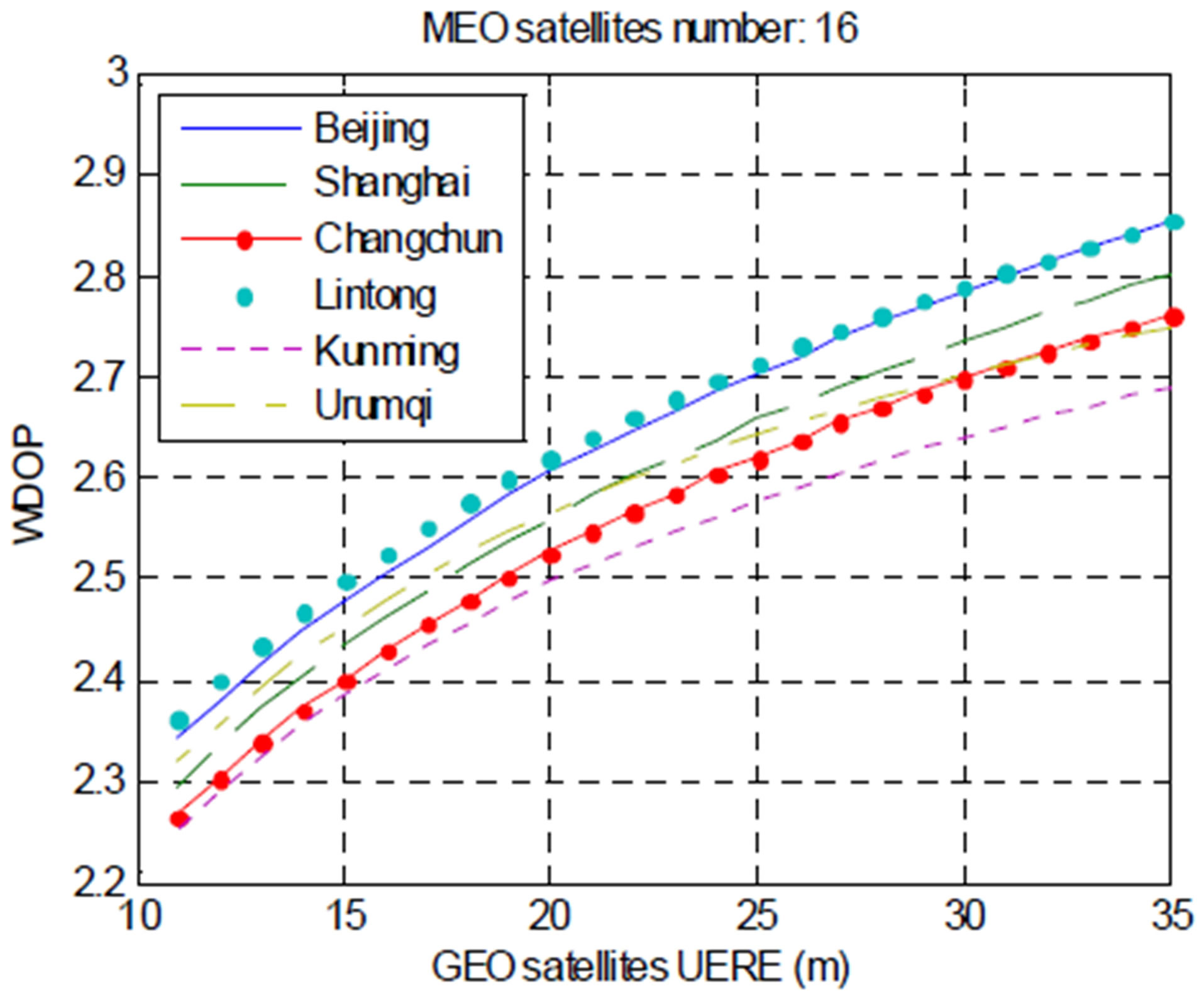 (b)
(b)
Figure 3. WDOP profiles for different ground stations. (a) WDOP vs. number of MEO satellites (GEO UERE fixed); (b) WDOP vs. GEO UERE (number of MEO satellites fixed).
are respectively 15.7 m, 17.4 m ,18.8 m, 15.0 m, 20.1 m, and 16.9 m for the 6 stations to meet the precision demand. We should also note that because the 6 chosen stations are relatively dense in terms of their geographic distribution, their individual observation geometries and the WDOP values have little difference. Therefore, their positioning precisions do not lead to much different inversions of the parameters. We can expect a larger impacts on the parameter inversions if the stations used are widely distributed all over the globe.
5. Conclusions
The construction of GNSS takes time. The satellites deployment of the constellation cannot be completed within a short time period. During the stepwise deployment procedure, the users’ demand for positioning precision needs to be satisfied as much as possible. In this paper, we considered the influences of the MEO satellites number and the GEO satellites UERE on the positioning precision. In such a constellation of mixed types of satellites, we selected the WDOP value as the evaluation criterion and theoretically analyzed the impact of selection of parameters on the WDOP. By using computer simulation, we provided the levels of positioning precision for two types of users under different deployment scenarios as well as the inversion of the parameters to satisfy the requirements of specified positioning precision.
The analysis and the inversion methods developed in this paper can be practically employed as a reference for designing the strategy of satellites deployment and the standards of system performance. We should also notice that among the performance measures, precision or accuracy is not the only index. The metrics of integrity, availability, continuity along with some other requirements and constraints should be considered.
6. Acknowledgements
This work was supported by the National Natural Science Foundation of China (NSFC, No. 60902089). Thanks also go to Prof. Jeffrey Yi-Lin, Forrest Department of Mathematics, Slippery Rock University for his advice and polishing of the manuscript.
REFERENCES
- S. S. Jan, T. Walter and P. Enge, “Reversion from L1-L5 dual to L5 Single Frequency WAAS in the Presence of RF Interference,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 46, No. 3, 2010, pp. 1110-1126. http://dx.doi.org/10.1109/TAES.2010.5545177
- W. H. Jiao, Q. Ding, J. W. Li, et al., “Monitoring and Assessment of GNSS Open Services,” The Journal of Navigation, Vol. 64, Suppl. S1, 2011, pp. S19-S29. http://dx.doi.org/10.1017/S0373463311000385
- H. Z. Cui, C. Han, S. K. Wang, et al., “The Mission Design Tool for Hybrid Orbit Satellite Constellation about Configuration Design and Management Strategy,” 2010 3rd International Conference on Advanced Computer Theory and Engineering(ICACTE), Chengdu, 20-22 August 2010, pp. V4-364-V4-369.
- Y. L. Zhang, L. Fan, Y. Zhang, et al., “Theory and Design of Satellite Constellations,” Science Press, Beijing, 2008, pp. 195-212 (in Chinese).
- Y. X. Yang, “Progress, Contribution and Challenges of Compass/Beidou Satellite Navigation System,” Acta Geodaetica et Cartographica Sinica, Vol. 39, No. 1, 2010, pp. 1-6 (in Chinese).
- W. J. Wu, Z. G. Li, X. H. Yang, et al., “Satellite Orbit Determination and Time Transfer Based on TWSTFT,” 2011 Joint Conference of the IEEE International Frequency Control Symposium and the European Frequency and Time Forum (FCS), San Francisco, 2-5 May 2011, pp. 1-4.
- J. C. Yoon, K. H. Lee, B. S. Lee, et al., “Geostationary Orbit Determination for Time Synchronization Using Analytical Dynamic Models,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 40, No. 4, 2004, pp. 1132-1146. http://dx.doi.org/10.1109/TAES.2004.1386869
- Z. G. Li, X. H. Yang, G. X. Ai, et al., “A New Method for Determination of Satellite Orbit by Transfer,” Science in China Series G: Physics Mechanics and Astronomy, Vol. 52, No. 3, 2009, pp. 384-392. http://dx.doi.org/10.1007/s11433-009-0057-6
- T. H. Xu, G. C. Xu, X. Shen, et al., “A Maneuvered GEO Satellite Orbit Determination Using Robustly Adaptive Kalman Filter,” 2010 International Conference on Intelligent System Design and Engineering Application, Changsha, 13-14 October 2010, pp. 55-59. http://dx.doi.org/10.1109/ISDEA.2010.82
- H. Sairo, D. Akopian and J. Takala, “Weighted Dilution of Precision as Quality Measure in Satellite Positioning,” IEE Proceedings Radar, Sonar and Navigation, Vol. 150, No. 6, 2003, pp. 430-436.
- P. Misra and P. Enge, “Global Positioning System: Signals, Measurements, and Performance,” Ganga-Jamuna Press, Lincoln, 2006, pp. 200-218.
- N. Blanco-Delgado and F. D. Nunes, “Satellite Selection Based on WDOP Concept and Convex Geometry,” 2010 5th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing (NAVITEC), Noordwijk, 8-10 December 2010, pp. 1-8.

