Open Journal of Statistics
Vol.3 No.3(2013), Article ID:33225,6 pages DOI:10.4236/ojs.2013.33019
Application of Non-Linear Cobb-Douglas Production Function with Autocorrelation Problem to Selected Manufacturing Industries in Bangladesh
1Department of Statistics, Islamic University, Kushtia, Bangladesh
2Department of Statistics, Jahangirnagar University, Dhaka, Bangladesh
Email: mmhrs.iustat@gmail.com, tapati555@yahoo.com, ajitm@ewubd.edu
Copyright © 2013 Md. Moyazzem Hossain et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received November 22, 2012; revised February 25, 2013; accepted March 4, 2013
Keywords: Cobb-Douglas Production Function; Autocorrelation; Manufacturing Industry; Bangladesh
ABSTRACT
In developing counties, efficiency of economic development has been determined by the analysis of industrial production. An examination of the characteristic of industrial sector is an essential aspect of growth studies. The growth of a country can be measured by Gross Domestic Product (GDP). GDP is substantially affected by the industrial output. Industrial gross output is mainly a function of capital and labor input. If the effect of labor and capital input to output is at a satisfactory level in an industry or in a group of industries, then industrial investment will increase. As a result, the number of industries will increase, which will directly affect GDP and also will decrease the unemployment rate. This is why, industrial input-output relationship is so important for any industry as well as for the overall industrial sector of a country. To forecast the production of a firm is necessary to identify the appropriate model. MD. M. Hossain et al. [1] have shown that Cobb-Douglas production function with additive errors was more suitable for some selected manufacturing industries in Bangladesh. The main purpose of this paper is to detect the autocorrelation problem of CobbDouglas production model with additive errors. The result shows that autocorrelation is presented in some manufacturing industries. Finally, this paper removes the autocorrelation problem and re-estimates the parameters of the CobbDouglas production function with additive errors.
1. Introduction
In the present times, production takes place by the combination forces of various factors of production such as land, labor, capital etc. In this connection, socialist countries are using different patterns of level of factors of production for their respective industrialization policy according to the taste, demand and nature of their countrywide population, its size, location and environment. Bangladesh is a developing country. It is essential for Bangladesh to go for mass industrialization to strengthen the economy of Bangladesh for this purpose; of course our policy for industrialization must be well planned, well defined and well thoughtful. The development of economy is dependent on the industrial polices of the country. By using production function we can get industrial policies especially indication about the nature of the production inputs used in the production function.
The growth of a country can be measured by Gross Domestic Product (GDP). GDP is substantially affected by the industrial output. Industrial gross output is a function of capital and labor input mainly. If the effect of labor and capital input to output is at a satisfactory level in an industry or in a group of industries, then industrial investment will increase. As a result, the number of industries will increase, which will directly affect GDP and also will decrease the unemployment rate. This is why, industrial input-output relationship is so important for any industry as well as for the overall industrial sector of a country.
Hoque [2], Bhatti [3], Baltagi [4], Bhatti and Owen [5], Bhatti [6], Bhatti et al. [7], Ingene and Lusch [8], Mok [9], Hossain et al. [10], Hajkova and Hurnik [11], Prajneshu [12], Antony [13], Hossain et al. [14], amongst others who have used linear regression models to measure the log-linear Cobb-Douglas (C-D) type production processes. Hoque [2] used the survey data for Bangladesh to examine the relationship between farm size and production efficiency. The author estimated two CobbDouglas-type production functions both by ordinary least squares with fixed and random coefficients. The stochastic term in Cobb-Douglas type models is either specified to be additive or multiplicative (See Stephen M. Goldfeld and Richard E. Quandt [15]). They developed a model in which a Cobb-Douglas type function is coupled with simultaneous multiplicative and additive errors. But MD. M. HOSSAIN ET AL. [1] have been shown that CobbDouglas production function with additive errors was more suitable for some selected manufacturing industries in Bangladesh. They used the annual industrial data collected from the recent publications of “Statistical Yearbook of Bangladesh” [16] published by Statistics division, Ministry of Planning, Dhaka, Bangladesh and “Report on Bangladesh Census of Manufacturing Industries (CMI)” [17] published by Planning division, Ministry of Planning, Dhaka, Bangladesh, for the major manufacturing industries of Bangladesh over the period 1978-1979 to 2001-2002 to estimate the Cobb-Douglas production function. This paper also considers these data sets. Moreover, this paper could not use the latest data of manufacturing industries simply because the relevant data are not up to date in the ministry. This paper considers the following manufacturing industries for the ongoing analysis:
i) Textile, ii) Leather & Leather products, iii) Leather footwear, iv) Wood & cork products, v) Furniture & fixtures (wooden), vi) Paper & paper products, vii) Printing & publications, viii) Drugs & pharmaceuticals, ix) Chemical, x) Plastic products, xi) Glass & glass products, xii) Iron & steel basic industries, xiii) Fabricated metal products, xiv) Transport equipment, xv) Beverage and xvi) Tobacco.
Productions of a manufacturing industry during a specific period constitute time series data. In this situation autocorrelation is present. Thus in order to develop a model for production this paper consider autocorrelation problem. That is why the main purpose of this paper is detecting the autocorrelation problem of Cobb-Douglas production model with additive errors to measure the production process of some selected manufacturing industries in Bangladesh.
The rest of this paper is organized as follows. Section 2 briefly discusses the theoretical concepts of the CobbDouglas production function with additive errors. Section 3 discusses the estimation procedure of this model. Results and discussion have been presented in Section 4. Section 5 concludes the paper.
2. Cobb-Douglas Production Function
The Cobb-Douglas production function is the widely used function in Econometrics. A famous case is the well-known Cobb-Douglas production function introduced by Charles W. Cobb and Paul H. Douglas, although anticipated by Knut Wicksell and, some have argued, J. H. Von Thünen [18]. They have estimated it after studying different industries in the world, for this it is used as a fairly universal law of production.
The Cobb-Douglas production function with additive error term can be represented as,
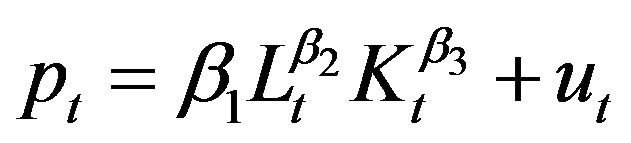 (2.1)
(2.1)
where,  is the output at time
is the output at time ;
;  is the Labor input;
is the Labor input; 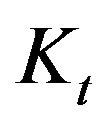 is the Capital input;
is the Capital input; 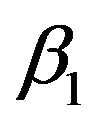 is a constant;
is a constant;  is the random error term.
is the random error term. 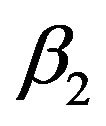 and
and  are positive parameters.
are positive parameters.
3. Estimation Procedure
In the case of Equation (2.1), the minimization of error sum squares  is no longer a simple linear estimation problem. To estimate the production function we need to know different types of non-linear estimation. In non-linear model it is not possible to give a closed form expression for the estimates as a function of the sample values, i.e., the likelihood function or sum of squares cannot be transformed so that the normal equations are linear. The idea of using estimates that minimize the sum squared errors is a data-analytic idea, not a statistical idea; it does not depend on the statistical properties of the observations (see Christensen [19]). Newton-Raphson is one of the popular methods to estimate the parameters in non-linear system.
is no longer a simple linear estimation problem. To estimate the production function we need to know different types of non-linear estimation. In non-linear model it is not possible to give a closed form expression for the estimates as a function of the sample values, i.e., the likelihood function or sum of squares cannot be transformed so that the normal equations are linear. The idea of using estimates that minimize the sum squared errors is a data-analytic idea, not a statistical idea; it does not depend on the statistical properties of the observations (see Christensen [19]). Newton-Raphson is one of the popular methods to estimate the parameters in non-linear system.
Newton-Raphson Method
Newton-Raphson is one of the popular Gradient methods of estimation. In Newton-Raphson method, we approximate the objective function  at
at 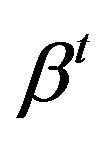 by Taylor series expansion up to the quadratic terms
by Taylor series expansion up to the quadratic terms
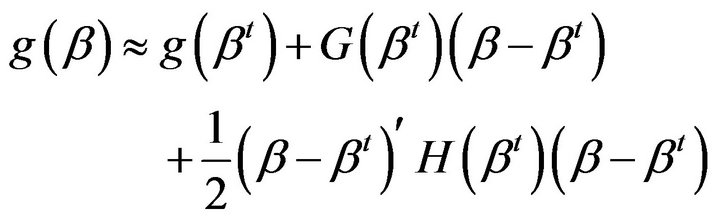
where,  is the gradient vector and
is the gradient vector and
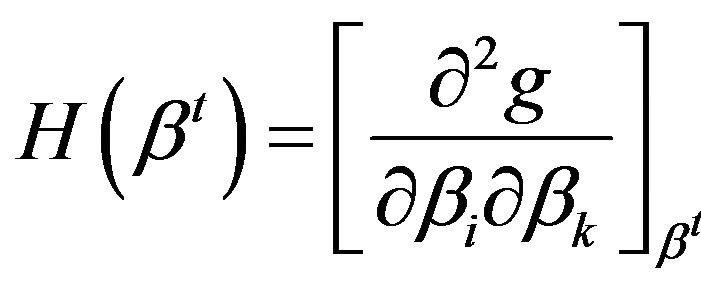 is the Hessian matrix. This Hessian matrix is positive definite, the maximum of the approximation
is the Hessian matrix. This Hessian matrix is positive definite, the maximum of the approximation 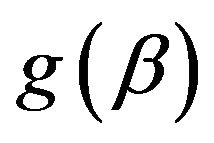 occurs when its derivative is zero.
occurs when its derivative is zero.
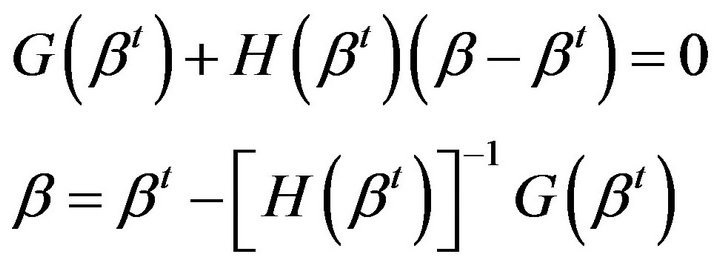
This gives us a way to compute , the next value in iterations is,
, the next value in iterations is,

The iteration procedures continue until convergence is achieved. Near the maximum the rate of convergence is quadratic as define by
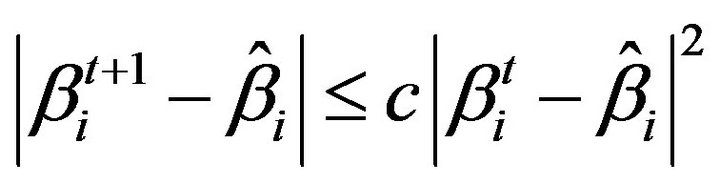
for some  when
when 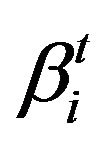 is near
is near 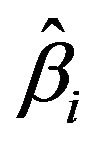 for all
for all . Thus we get estimates
. Thus we get estimates 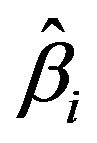 by Newton-Raphson methods.
by Newton-Raphson methods.
For the model (2.1), to estimate the parameters we minimize the following error sum squares

In case of nonlinear estimation we use the score vector and Hessian matrix. The elements of score vector are given below:

Also the elements of Hessian matrix are given below:
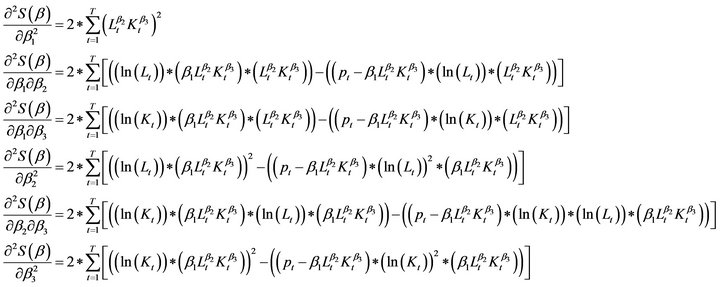
Hence the Score vector is

and Hessian matrix is

4. Results and Discussion
The parameters of the Cobb-Douglas production function with additive errors have been estimated by using optimization subroutine for different manufacturing industries considered in this study. The results are summarized in the Table 1.
There are economies of scale in the manufacturing of Drugs & pharmaceuticals, Furniture & fixtures (wooden), Iron & steel basic, Leather footwear, Fabricated metal products, Plastic products, Printing & publications, Tobacco since  for these industries and there are diseconomies of scale in the Beverage, Chemical, Glass & glass products, Leather & leather products, Paper & paper products, Textile, Wood & crock products industries, Transport equipment since
for these industries and there are diseconomies of scale in the Beverage, Chemical, Glass & glass products, Leather & leather products, Paper & paper products, Textile, Wood & crock products industries, Transport equipment since 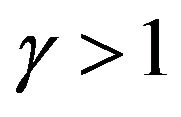 for these industries.
for these industries.
Results of Autocorrelation
The present study considers Durbin-Watson d test procedure to detect the presence of autocorrelation. In some
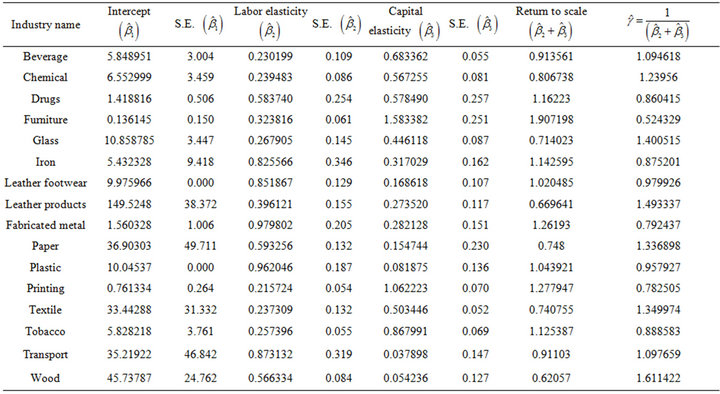
Table 1. The estimates of Cobb-Douglas production function with additive errors for different industries under study.
of the cases d statistic fails to detect autocorrelation. The limits of d are obtained at 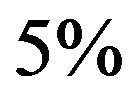 level of significance. Here, for
level of significance. Here, for 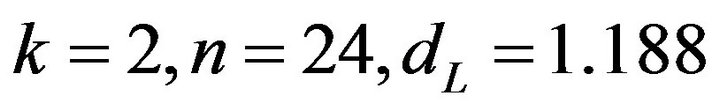 and
and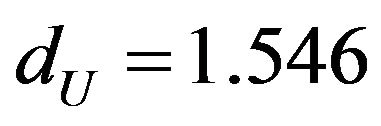 , where,
, where,  is the number of explanatory variables excluding the constant term and
is the number of explanatory variables excluding the constant term and ![]() is the total number of observations.
is the total number of observations.
In many situations, however, it has been found that the upper limit 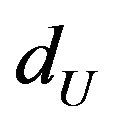 is approximately the true significance limit and therefore, in case the estimated d values lies in the indecision zone, one can use the modified d test procedure (See D. N. Gujarati [20]). By using these test procedures the present analysis found that, there exists positive autocorrelation of some manufacturing industries considered in this study.
is approximately the true significance limit and therefore, in case the estimated d values lies in the indecision zone, one can use the modified d test procedure (See D. N. Gujarati [20]). By using these test procedures the present analysis found that, there exists positive autocorrelation of some manufacturing industries considered in this study.
The results given in Table 2 indicates that, the autocorrelation is present in Beverage, Drug, Furniture, Iron, Leather footwear, Leather products, Paper, Plastic, Textile, Transport and Wood industry for Cobb-Douglas model with additive error terms. In order to remove this autocorrelation at first it is essential to estimate the value of . Theil-Nagar procedure is used to estimate the value of
. Theil-Nagar procedure is used to estimate the value of  in this study.
in this study.
Theil and Nagar have suggested that in small samples  can be estimated as
can be estimated as
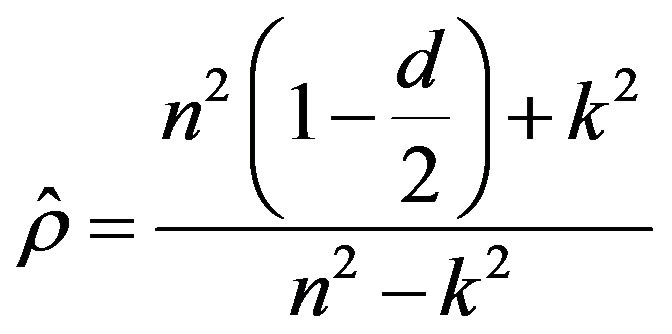
where, n = total number of observations, d = DurbinWatson d, and k = number of coefficients (including the

Table 2. Result for testing autocorrelation for the CobbDouglas production function with additive errors for selected industries under study.
intercept) to be estimated (See D. N. Gujarati [20]).
After estimating the value of , observation is transformed as
, observation is transformed as 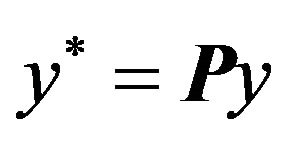 and
and 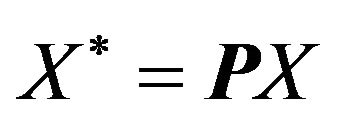 where
where 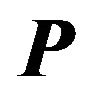 a matrix defined as
a matrix defined as
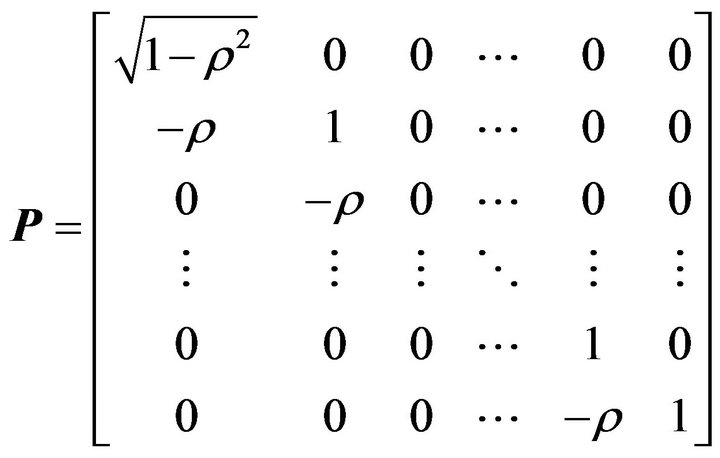
The present study fit again the model for transformed data by using Newton-Rapson method and obtained the following estimates.
The results provided in Table 3, indicates that the problem of autocorrelation successfully removed by taking suitable steps. After removing the autocorrelation problem, again the parameters of the Cobb-Douglas production function with additive errors is estimated. The estimates are given in Table 4.
5. Conclusion
Nowadays, businessmen as well as industrialists are very much concerned about the theory of firm in order to make correct decisions regarding what items, how much and how to produce them. To forecast the output of some selected manufacturing industries in Bangladesh it is necessary to the estimate the parameters of Cobb-Douglas production function with additive errors. This paper detects the autocorrelation problem of Cobb-Douglas production model with additive errors which is used to measure the production process of some selected manu-
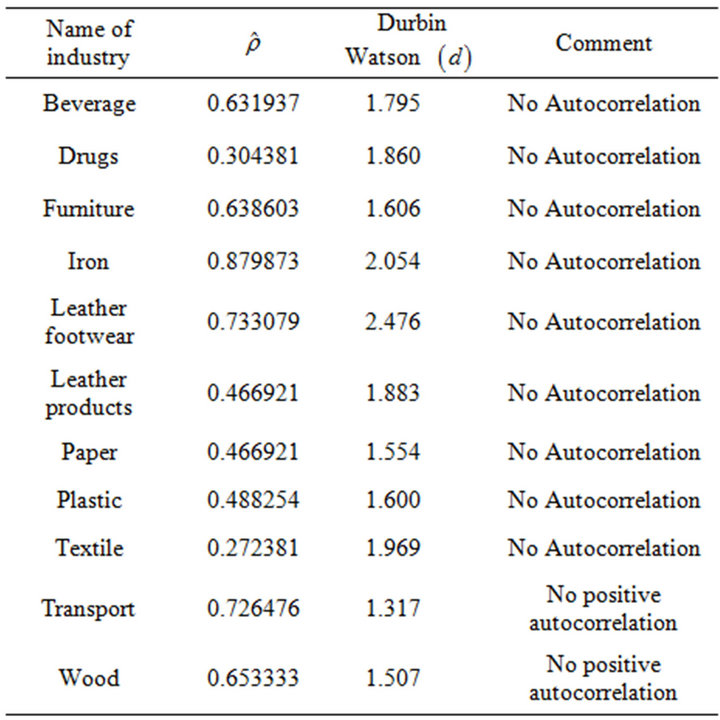
Table 3. Result for testing autocorrelation for the CobbDouglas production function with additive error in different industries for transformed data.
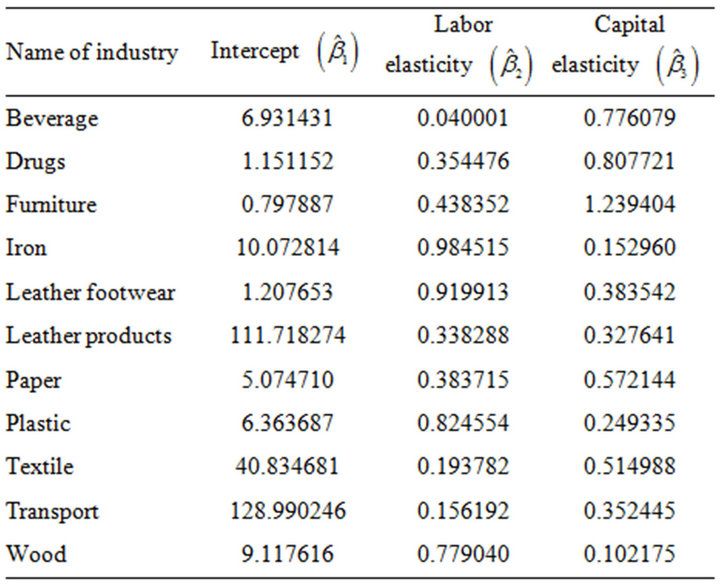
Table 4. Results of Cobb-Douglas production function with additive errors for transformed data.
facturing industries in Bangladesh. The results of this study show that the autocorrelation is presented in Beverage, Drug, Furniture, Iron, Leather footwear, Leather products, Paper, Plastic, Textile, Transport and Wood industry for Cobb-Douglas model with additive error terms. Finally, after removing the autocorrelation problem, the parameters of the production function is estimated.
REFERENCES
- M. Hossain, A. Majumder and T. Basak, “An Application of Non-Linear Cobb-Douglas Production Function to Selected Manufacturing Industries in Bangladesh,” Open Journal of Statistics, Vol. 2 No. 4, 2012, pp. 460-468. doi:10.4236/ojs.2012.24058
- I. Hoque, “An Application and Test of Random Coefficient Model in Bangladesh Agriculture,” Journal of Applied Econometrics, Vol. 6, No. 1, 1991, pp. 77-90. doi:10.1002/jae.3950060107
- M. I. Bhatti, “Efficient Estimation of Random Coefficient Models Based on Survey Data,” Journal of Quantitative Economics, Vol. 9, No. 1, 1993, pp. 99-110.
- B. H. Baltagi, “Econometrics Analysis of Panel Data,” John Wiley, New York, 1996.
- M. I. Bhatti and D. Owen, “An Econometrics Analysis of Agricultural Performance in Sichuan, China,” Asian Profile, Vol. 26, No. 6, 1996, pp. 443-57.
- M. I. Bhatti, “A UMP Invariant Test for Testing Block Effects: An Example,” Far East Journal of Theoretical Statistics, Vol. 1, No. 1, 1997, pp. 39-50.
- M. I. Bhatti, I. H. Khan and C. Czerkawski, “Agricultural Productivity in Shanghai Region of China: An Econometric Analysis,” Journal of Economic Sciences, Vol. 1, No. 2, 1998, pp. 1-12.
- C. A. Ingene and R. F. Lusch, “Estimation of a Department Store Production Function,” International Journal of Physical, Distribution & Logistics Management, Vol. 29, No. 7-8, 1999, pp. 453-464. doi:10.1108/09600039910371138
- V. W. K. Mok, “Industrial Productivity in China: The Case of the Food Industry in Guangdong Province,” Journal of Economic Studies, Vol. 29, No. 6, 2002, pp. 423-431. doi:10.1108/01443580210448853
- M. Z. Hossain, M. I. Bhatti and M. Z. Ali, “An Econometric Analysis of Some Major Manufacturing Industries: A Case Study,” Managerial Auditing Journal, Vol. 19, No. 6, 2004, pp. 790-795. doi:10.1108/02686900410543895
- A. D. Hajkova and J. Hurnik, “Cobb-Douglas Production Function: The Case of a Converging Economy,” Czech Journal of Economics and Finance, Vol. 57, No. 1, 2007, pp. 9-10.
- Prajneshu, “Fitting of Cobb-Douglas Production Functions: Revisited,” Agricultural Economics Research Review, Vol. 21, No. 2, 2008, pp. 289-292.
- J. Antony, “A Dual Elasticity of Substitution Production Function with an Application to Cross-Country Inequality,” Economics Letters, Vol. 102, No. 1, 2009, pp. 10-12. doi:10.1016/j.econlet.2008.09.007
- M. Z. Hossain and K. S. Al-Amri, “Use of Cobb-Douglas Production Model on Some Selected Manufacturing Industries in Oman,” Education, Business and Society: Contemporary Middle Eastern Issues, Vol. 3 No. 2, 2010, pp. 78-85. doi:10.1108/17537981011047925
- S. M. Goldfeld and R. E. Quandt, “The Estimation of Cobb-Douglas Type Functions with Multiplicative and Additive,” International Economic Review, Vol. 11, No. 2, 1970, pp. 251-257. doi:10.2307/2525667
- “Statistical Year Book,” 5th Edition, 7th Edition, 16th Edition, 18th Edition, 21st Edition, 22nd Edition, 24th Edition, Bangladesh Bureau of Statistics, Statistics Division, Ministry of Planning, Dhaka, 1984, 1986, 1995, 1997, 2000, 2001, 2003.
- “Reports on Bangladesh Census of Manufacturing Industries,” Bangladesh Bureau of Statistics, Planning Division, Ministry of Planning, Dhaka, 1984, 1987, 1992, 1997, 2000, 2002, 2004.
- C. W. Cobb and P. H. Douglas, “A Theory of Production,” American Economic Review, Vol. 18, No. 1, 1928, pp. 139-165.
- R. Christensen, “Advance Linear Modeling,” 2nd Edition, Springer, New York, 2001. doi:10.1007/978-1-4757-3847-6
- D. N. Gujarati, “Basic Econometrics,” 4th Edition, McGraw- Hill, New York, 1995.

