ABSTRACT

Two-stage adaptive cluster sampling and two-stage conventional sampling designs were used to estimate population total of Fringe-Eared Oryx that are clustered and sparsely distributed. The study region was Amboseli-West Kilimanjaro and Magadi-Natron cross boarder landscape between Kenya and Tanzania. The study region was partitioned into different primary sampling units with different secondary sampling units that were of different sizes. Results show that two-stage adaptive cluster sampling design is efficient compared to simple random sampling and the conventional twostage sampling design. The design is less variable compared to the conventional two-stage sampling design.

1. Introduction

The Fringe-eared Oryx is one of the subspecies of Oryx gazelle. They range from the grassland of Northern Eastern Tanzania to Southern Kenya [1] and they are conservation dependent species. Currently, the species is not listed as an endangered species but its populations are declining [1]. This is partly because in the past, they were hunted for their tough skin by European settlers [2] and recently they are being gunning down by poachers for their horns. The other causes for their decline are uncontrolled hunting for sport [1] and just like other wildlife, human encroachment to protected areas and land use changes [3] have led to the reduction in their numbers. The Fringe-Eared Oryx lives in clustered herds that vary in sizes from a few to hundreds of individuals [2] and are sparsely distributed [4]. They are mobile and can travel for long distances in search for food [1] since rainfall within Amboseli ecosystem is unevenly distributed [3]. To ensure adequate conservation and management of Fringe-Eared Oryx, knowledge of their numbers is critical.

Adaptive cluster sampling (ACS) was suggested for sampling populations that are clustered and rare [5]. ACS in which the initial sample is selected by simple random sampling with or without replacement was described by [5], where the initial sample is selected by systematic sampling was described by [6]. Ratio estimators in ACS were described by [7]. Smith [8] applied ACS to estimate density of wintering Waterfowl while [9] applied ACS to estimate abundance within local populations of low abundance plants.

Cochran [10] described two-stage (TS) sampling that is suitable when sampling large areas [11]. This is as a result of lower costs incurred when sampling selected PSUs rather than moving across the study area to perform sampling. PSUs [12] described two-stage adaptive cluster sampling (TSA) which is a combination of ACS and TS sampling designs. Smith [11] applied TSA to estimate density and abundance of fresh water mussels in the Upper Mississippi River using simulated data.

In this study, we evaluate the efficiency of TS and TSA sampling designs in estimating population total of FringeEared Oryx in Amboseli-West Kilimanjaro and MagadiNatron cross border landscape using data from aerial survey conducted in 2010 by KWS and other partners. Section two briefly describes the theory of TSA design, section three gives the method for the current study, section four gives results, and section five has the discussion and conclusion.

2. Two-Stage Adaptive Cluster Sampling Design

In the TSA design, which was proposed by [12], information from a pilot survey is used to design an efficient sampling procedure by controlling the final sample size and sampling cost. In this design, the study region consisting of units is partitioned into 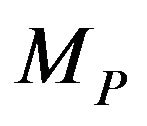primary sampling units (PSUs) each with 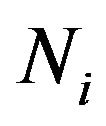secondary sampling units (SSUs) where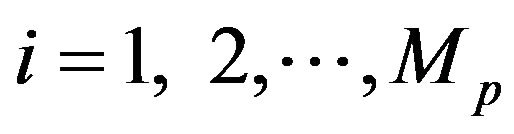. Let 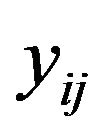be the observed value in 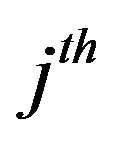secondary unit of 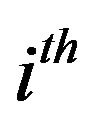primary unit and let 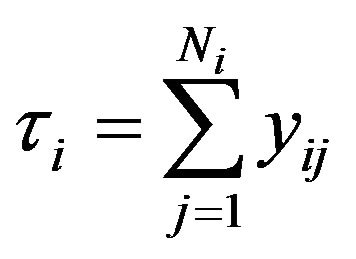be the sum of the observed values in the 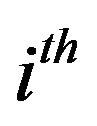primary unit.

In the first stage, 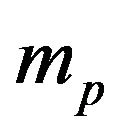primary units are selected from units by simple random sampling (SRS) without replacement. In the second stage 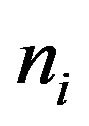secondary units are selected from primary unit i, where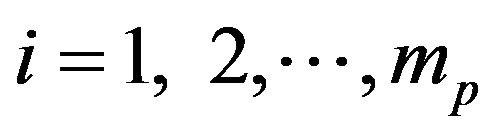, using simple random sampling without replacement. If any selected secondary unit meets a condition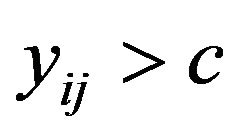, neighboring units are added. If any of the added units meets the condition, still more units are added. The procedure continues until there are clusters of units each with units that meet the condition (network) surrounded by units that do not meet the condition (edge units). A neighborhood of a unit consists of itself plus its adjacent units on the North, East, West and South. The procedure results in two situations [12], where clusters intersect more than one PSUs (overlapping scheme) and where clusters are truncated at the boundary of PSUs (non-overlapping scheme).

Salehi and Seber [12], derived two design unbiased estimators, Horvitz-Thompson (HT) and Hansen-Hurwitz (HH) estimators. We consider the non-overlapping scheme since the estimators are more efficient compared to overlapping scheme [12]. We also make use of the HT estimator since it is more efficient compared to HH estimator [5,12].

Let 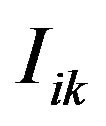be an indicator function that is one if the initial sample intersect network k and zero otherwise, let  be the number of networks in primary unit i, 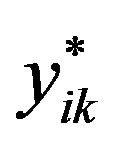the sum of observed values in network k of primary unit i and 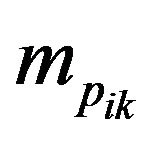be the number of units in network k in primary unit i, then the partial inclusion probability, that is the probability that units in the initial sample of primary unit I intersect network k, is given by [12]

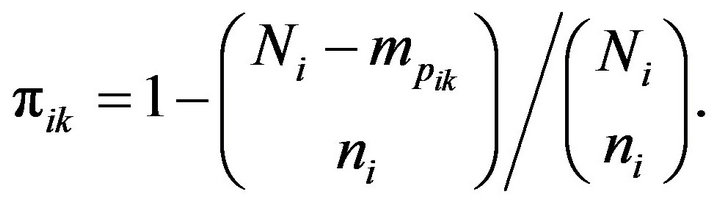
The HT estimator is thus given by [12]

where. The second order partial inclusion probability is given by [12]

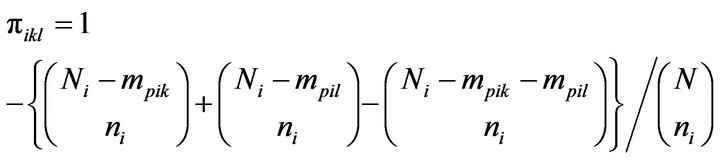
Let the variance for the PSUs be

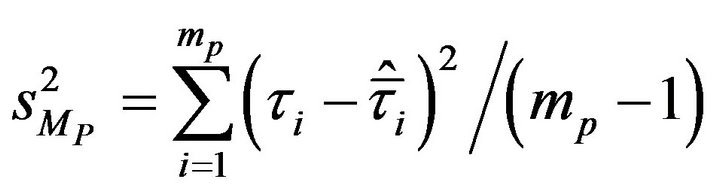
and the variance for SSUs b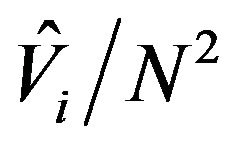e where

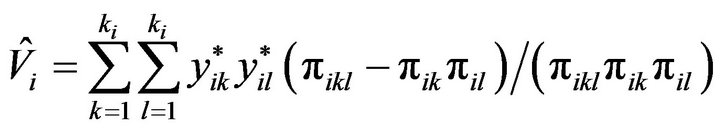with the number of distinct networks intersected by primary unit i, an unbiased estimator of the variance of HT is given by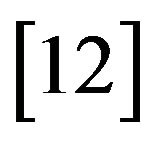

3. Method

Amboseli-West Kilimanjar/Magadi–Natron cross-border landscape stretches between Kenya and Tanzania. The landscape was placed on a rectangular grid which is, for the purpose of this study, the study area. The study area was divided into 24 × 18 squared units each measured 69.44 km². Similar to [13], the study area was partitioned into 6, 12 and 18 PSUs based on the survey report [4] on the degree of rarity and clusteredness of Fringe-Eared Oryx in the study area. This enabled the study of large, medium and small sized PSUs where each measured 4999.68 km², 2499.84 km² and 1666.56 km² respectively. For the adaptive design, the condition to adaptively add units was.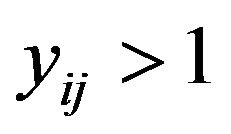

The sample sizes for large sized PSUs, 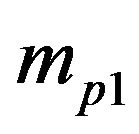, were 2 and 3, for medium sized PSUs were 4 and 6 and for small sized PSUs were 6 and 9. Initial sample sizes for secondary units, 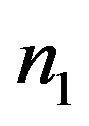, were 2, 3 and 4 in all cases for adaptive design. The sample size for SSUs for the non-adaptive design was set up to the effective sample size for the adaptive design.

Two-stage adaptive and non-adaptive designs were considered. In each case, re-sampling was carried out 1000 times. Efficiency was obtained as

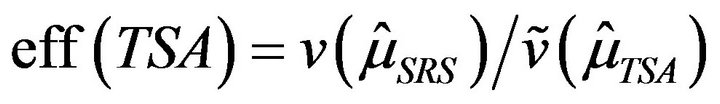for adaptive and

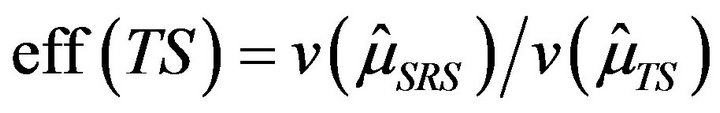for non-adaptive design. Population total and variance were obtained as

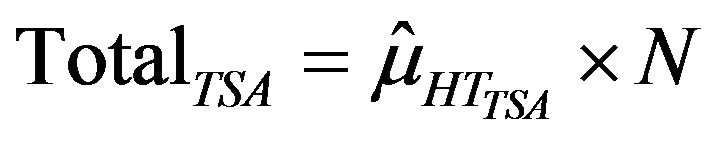and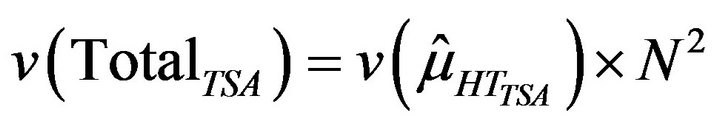

for adaptive design an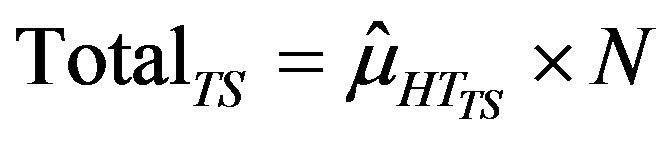d and

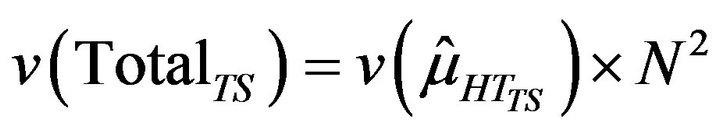for non-adaptive designs respectively. For adaptive design only, the effective sample size was obtained as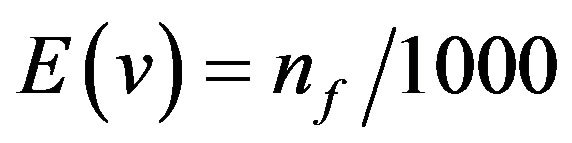, that is, the average number of units in the final sample over the number of re-sampling. Estimates were obtained using Program SAMPLE [11].

4. Results

Results are shown in Table 1 below. From the table, TSA

design has higher efficiency compared to the non-adaptive (TS) design. The adaptive design is efficient compared to SRS irrespective of the number or size of PSUs. Efficiency for the non-adaptive design is attained only when the study region is divided into 18 PSUs and using a sample size of 9 for PSUs.

For both adaptive and non-adaptive designs, Efficiency increases with increasing in number of units in PSUs in the study region as well as the sample size of PSUs and initial sample size/sample size for SSUs.

While the survey recorded a total of 196 Fringe-Eared Oryx [4], the population was estimated to range from 189 to 206 when adaptive design is used and from 192 to 225 upon use of non-adaptive design when the study region is partitioned into 6 PSUs. When the study region is partitioned into 12 PSUs, the total population for Fringe-Eared Oryx was estimated to range from 191 to 203 and from 191 to 207 when adaptive and non-adaptive designs are used respectively. Finally, Fringe-Eared Oryx are estimated to be between 185 and 201 using adaptive design and between 184 and 200 using non adaptive design for a study region that is partitioned into 18 PSUs.

Variation decreases with increasing initial sample size for SSUs, initial sample size for PSUs and the size of PSUs for both designs. TSA design is more reliable since it reports lower values of coefficient of variation compared to TS design.

For the adaptive design, the effective sample size is a function of the unit size of PSUs, sample size of PSUs and initial sample size of SSUs.

5. Discussion and Conclusions

Salehi and Seber [12] proposed a TSA due to its suitability in performing a pilot survey so as to design an experiment with a given precision of estimation. TS designs are economical designs when sampling such a large study area since they reduce movement within the large study area [11]. Since populations of Fringe-Eared Oryx are declining [4] and noting the vastness of the study area, TSA could be applied to for conservation purposes. Small initial sample sizes (2, 3 and 4) for secondary units were used for adaptive design; this was to avoid the negative variances on individual PSUs [12].

Results show that the size, 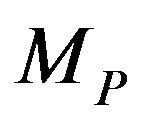, and the sample size, 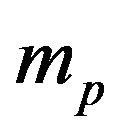, for PSUs as well as the initial sample size/sample size for SSU have an effect on the efficiency and amount of variance on the two-stage sampling for both adaptive and non-adaptive designs. The adaptive design resulted in higher efficiency with lower variance compared to the non-adaptive design. These results agree with [5] that adaptive designs result if higher efficiency and lower variance compared to conventional sampling designs.

For this study, highest precision is attained when the study region was partitioned into 18 PSUs each with 24 SSUs and where initial sample size for PSUs, 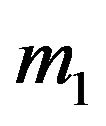, is 9. The TSA still has a drawback of the final sample size. Further controlling the final sample size with this design deserves further study.

6. Acknowledgement

J. W. Mwangi and M. E. Salim thank David Smith for helpful comments of the previous version.

REFERENCES

NOTES

^*Corresponding author.