Open Journal of Statistics
Vol.3 No.2(2013), Article ID:29912,9 pages DOI:10.4236/ojs.2013.32009
Composite Quantile Regression for Nonparametric Model with Random Censored Data
Department of Mathematics, Tongji University, Shanghai, China
Email: jrtrying@126.com, wmqian2003@yahoo.com.cn
Copyright © 2013 Rong Jiang, Weimin Qian. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 29, 2012; revised June 30, 2012; accepted July 15, 2012
Keywords: Kaplan-Meier Estimator; Censored Data; Composite Quantile Regression; Kernel Estimator; Nonparametric Model
ABSTRACT
The composite quantile regression should provide estimation efficiency gain over a single quantile regression. In this paper, we extend composite quantile regression to nonparametric model with random censored data. The asymptotic normality of the proposed estimator is established. The proposed methods are applied to the lung cancer data. Extensive simulations are reported, showing that the proposed method works well in practical settings.
1. Introduction
Consider the following nonparametric regression model with random censored data:
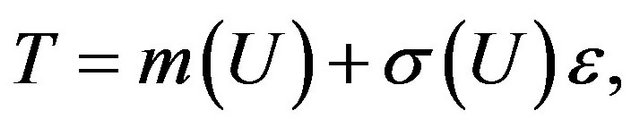 (1)
(1)
where  is an unknown smoothing function,
is an unknown smoothing function, 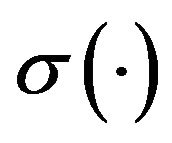 is a positive function representing the standard deviation and
is a positive function representing the standard deviation and ![]() is the random error with mean 0 and variance 1. Let C denote the censoring variable, whose distribution may depend on U, where U is vector of observed covariates. In this paper, we focus on random right censoring, we only observe the triples
is the random error with mean 0 and variance 1. Let C denote the censoring variable, whose distribution may depend on U, where U is vector of observed covariates. In this paper, we focus on random right censoring, we only observe the triples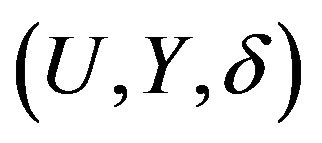 , where
, where  and
and  are the observed response variable and the censoring indicator respectively, where
are the observed response variable and the censoring indicator respectively, where ![]() is the survival time.
is the survival time.
Censored quantile regression was first studied by [1] for fixed censoring. [2] proposed an estimator for a conditional quantile assuming that the regression models at lower quantiles are all linear. A recursively weighted estimation procedure that can be regarded as a generalization of the Kaplan-Meier estimator to conditional quantiles was described in their paper. Afterward, [3] presented an alternative approach that is based on the Nelson-Aalen estimator of the cumulative hazard function but still requires the same global-linearity assumption as Portnoy’s. Their method provides a more direct approach to the asymptotic theory and a simpler computation algorithm. More recent studies by [4], proposed to overcome the global-linearity assumption by directly estimating the conditional censoring distribution nonparametrically using the local Kaplan-Meier method. Their computational algorithm is more stable and simpler to implement than Portnoy’s or Peng and Huang’s. Moreover, the local nonparametric estimator on which the model is based performs best when the covariates can be assumed independent.
Intuitively, the composite quantile regression (CQR) should provide estimation efficiency gain over a single quantile regression; see [5]. A composite quantile regression model assumes that there exist common covariate effects in a range of quantiles such that the quantile levels only differ in terms of the intercept. From a more general regression perspective, composite quantile regression seeks to model a set of parallel regression curves, and thus it can be viewed as a compromise between a set of quantile regression curves with different intercepts and slopes and a single summary regression curve. [6] proposed the local polynomial CQR estimators (LCQR) for estimating the nonparametric regression function and its derivative. It is shown that the local CQR method can significantly improve the estimation efficiency of the local least squares estimator for commonlyused non-normal error distributions. Furthermore, [7] studied semiparametric CQR estimates for semiparametric varying-coefficient partially linear model. They compared CQR with least squares and quantile regression, and the results showed that CQR outperformed both least squares and quantile regression. [8] considered CQR estimates for single-index models. Recently, [9] extended the CQR method to linear model with randomly censored data. This motivates us to extend the CQR method to nonparametric model with censored data (LCQRC).
The paper is organized as follows. In Section 2, local composite quantile regression for nonparametric model with censored data is introduced, and the main theoretical results are also given in this section. Both simulation examples and a real data application are given in Section 3 to illustrate the proposed procedures. Final remarks are given in Section 4. The technical proofs are deferred to the Appendix.
2. Methodology
2.1. Local Composite Quantile Regression with Censored Data
We first consider an ideal situation where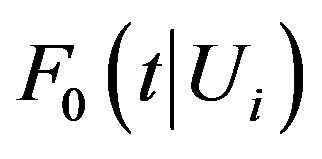 , the conditional cumulative distribution function of the survival time
, the conditional cumulative distribution function of the survival time ![]() given
given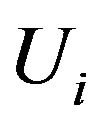 , is assumed to be known. In this case, we define the following weight function:
, is assumed to be known. In this case, we define the following weight function:
 (2)
(2)
 . In reality,
. In reality, 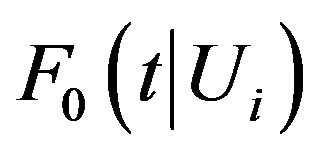 is unknown and has to be estimated. We propose to estimate
is unknown and has to be estimated. We propose to estimate 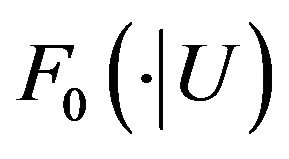 nonparametrically using the local Kaplan-Meier estimator
nonparametrically using the local Kaplan-Meier estimator
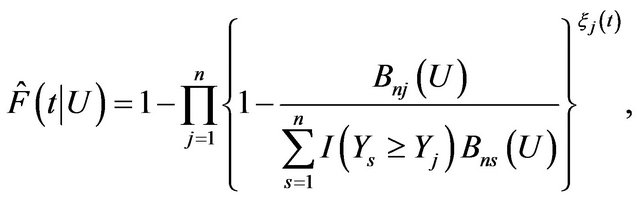
where 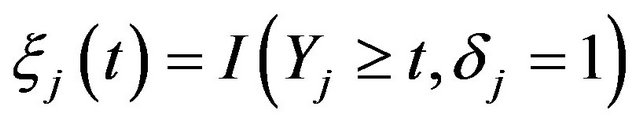 and
and
 , where
, where
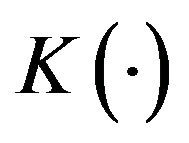 is a smooth kernel function,
is a smooth kernel function, 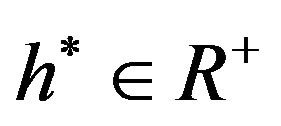 is the bandwidth converging to zero as
is the bandwidth converging to zero as![]() . By plugging
. By plugging 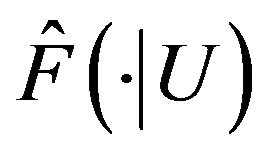 into (2), we obtain the estimated local weights
into (2), we obtain the estimated local weights
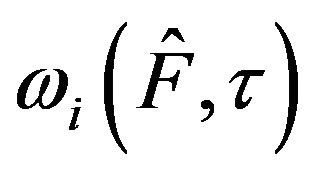 . Consider estimating the value of
. Consider estimating the value of 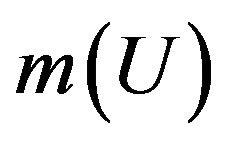 at
at
 . The LCQRC procedure estimates
. The LCQRC procedure estimates , defined by
, defined by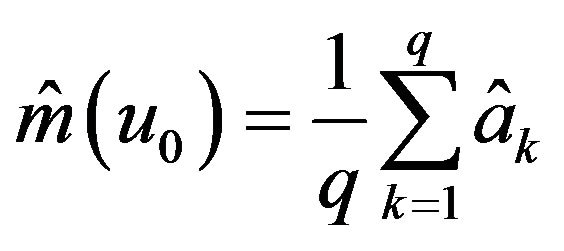 , via minimizing the locally weighted objective function
, via minimizing the locally weighted objective function
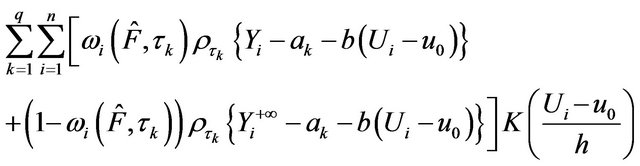
where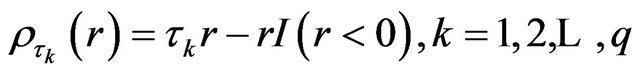 , be q check loss functions at q quantile positions:
, be q check loss functions at q quantile positions: 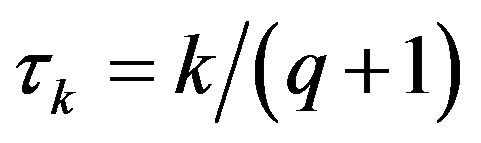 and
and 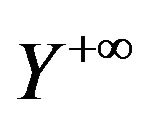 is any value sufficiently large to exceed all
is any value sufficiently large to exceed all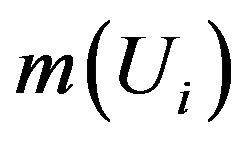 .
.
Remark 1. The detail explant of 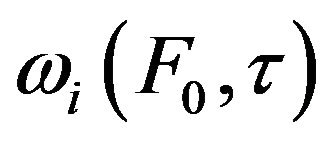 can see Remark 1 of [4].
can see Remark 1 of [4].
2.2. Asymptotic Properties
Denote by 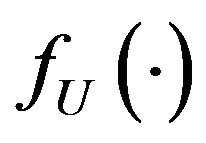 the marginal density function of the covariate
the marginal density function of the covariate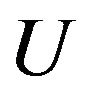 ,
, 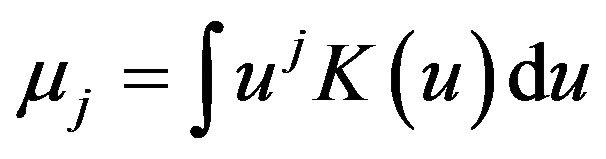 and
and
 . To prove main results in this paperthe following technical conditions are imposed.
. To prove main results in this paperthe following technical conditions are imposed.
A1. The functions 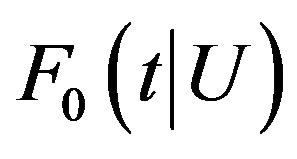 and
and 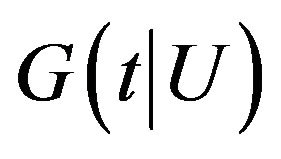 have first derivatives with respect to
have first derivatives with respect to , denoted as
, denoted as 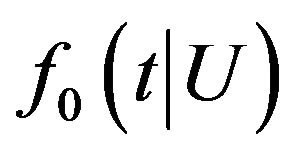 and
and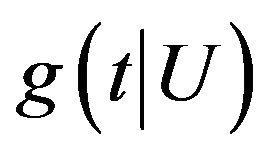 , which are uniformly bounded away from infinity. In addition,
, which are uniformly bounded away from infinity. In addition, 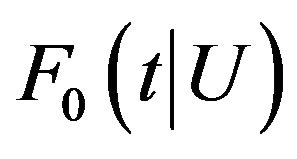 and
and 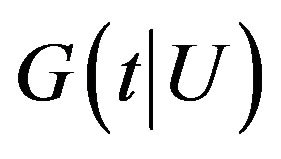 have bounded second order partial derivatives with respect to U.
have bounded second order partial derivatives with respect to U.
A2. ![]() is positive definite matrix.
is positive definite matrix.
A3. 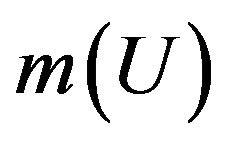 has a continuous second derivative in the neighborhood of
has a continuous second derivative in the neighborhood of .
.
A4. 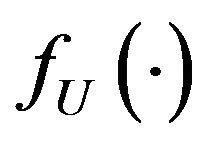 is differentiable and positive in the neighborhood of
is differentiable and positive in the neighborhood of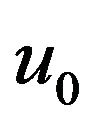 .
.
A5. The conditional variance 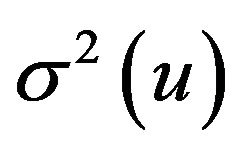 is continuous in the neighborhood of
is continuous in the neighborhood of .
.
A6. Assume that the error has a symmetric distribution with a positive density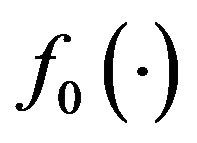 .
.
Remark 2. Assumption A1 is needed for the local Kaplan-Meier estimator. It allows us to obtain the local expansions of 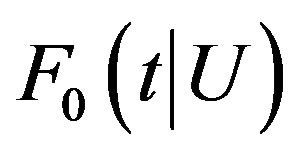 and
and 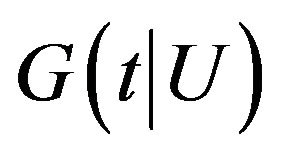 in the neighborhood of
in the neighborhood of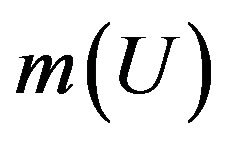 , and to obtain the uniform consistency and the linear representation of
, and to obtain the uniform consistency and the linear representation of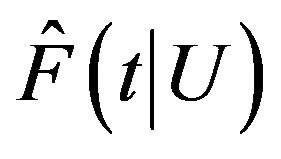 , which are needed for deriving the asymptotic normality result. Assumption A2 ensures that the expectation of the estimating function has a unique zero, and it is needed to establish the asymptotic distribution. Assumptions A3- A6 are the same conditions for establishing the asymptotic normality of local composite quantile regression ([6]).
, which are needed for deriving the asymptotic normality result. Assumption A2 ensures that the expectation of the estimating function has a unique zero, and it is needed to establish the asymptotic distribution. Assumptions A3- A6 are the same conditions for establishing the asymptotic normality of local composite quantile regression ([6]).
We state the asymptotic normality for 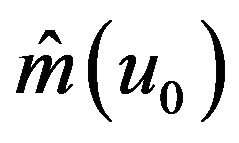 in the following theorem.
in the following theorem.
Theorem 1. Assume that the triples 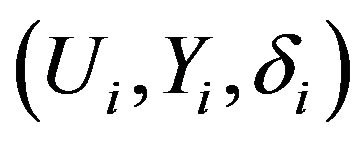 constitute and i.i.d. multivariate random sample, and that the censoring variable
constitute and i.i.d. multivariate random sample, and that the censoring variable 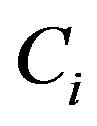 is independent of
is independent of ![]() conditional on the covariate
conditional on the covariate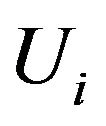 . Suppose that
. Suppose that 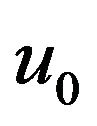 is an interior of the support of
is an interior of the support of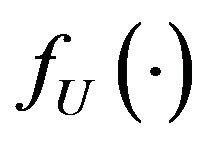 . Under the regularity conditions A1-A6, if
. Under the regularity conditions A1-A6, if  and
and , then
, then
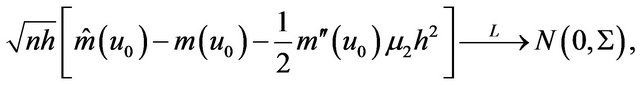
where 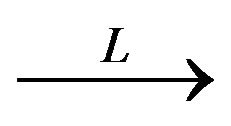 stands for convergence in distribution and
stands for convergence in distribution and
 , where
, where
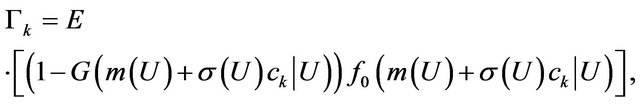
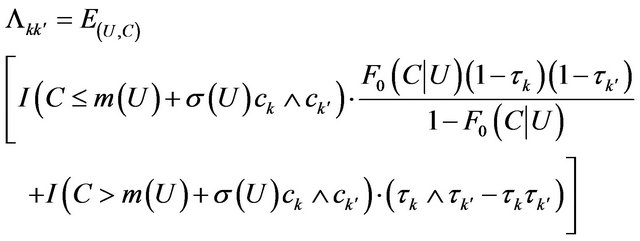
and .
.
3. Numerical Studies
In this section, we conduct simulation studies to assess the finite sample performance of the proposed procedures and illustrate the proposed methodology on a lung cancer data set. Moreover, we compare the performance of the newly proposed method with LCQR ([6]) and nonparametric quantile regression with censored data (NQRC) that was proposed by [10].
In the proposed compute process, we take
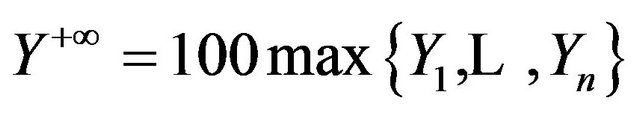 and
and
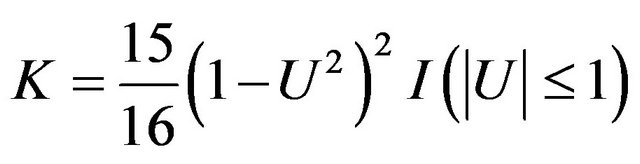 . The bandwidth h* can be obtained by 10-fold cross-validation method (see [4]), and we use the short-cut strategy method to select
. The bandwidth h* can be obtained by 10-fold cross-validation method (see [4]), and we use the short-cut strategy method to select  (see [6]).
(see [6]).
3.1. Example 1
The data are generated from the following model
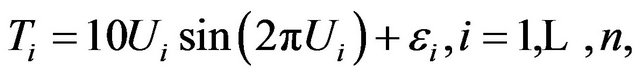
where  is uniformly distributed on
is uniformly distributed on 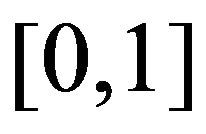 and
and ![]() is i.i.d. standard normal random variables. The censoring variable
is i.i.d. standard normal random variables. The censoring variable  and
and . The value of the constant c in the model determines the censoring proportion. In our simulations, we consider three censoring rates (CR): 20%, 30% and 40%. For each censoring rate, the sample sizes are taken to be 100 and 200. To evaluate the finite sample performance of our estimator. Two distance measures are approximated, the first one the mean absolute deviation error (MADE) is given by
. The value of the constant c in the model determines the censoring proportion. In our simulations, we consider three censoring rates (CR): 20%, 30% and 40%. For each censoring rate, the sample sizes are taken to be 100 and 200. To evaluate the finite sample performance of our estimator. Two distance measures are approximated, the first one the mean absolute deviation error (MADE) is given by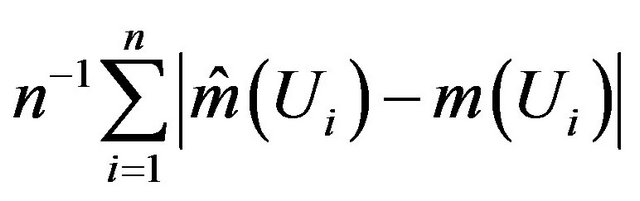 , and the second one the mean squared error (MSE) defines as
, and the second one the mean squared error (MSE) defines as
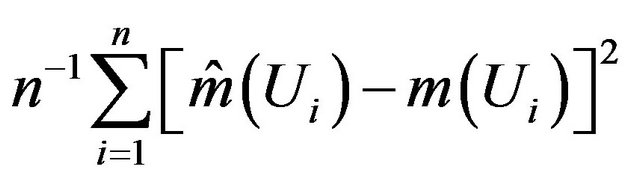 . Furthermore, we define the rate of MADE and MSE which are
. Furthermore, we define the rate of MADE and MSE which are
 and
and
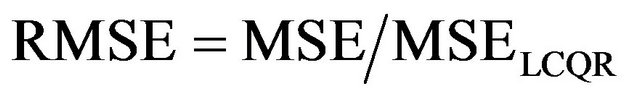 .
.
For right censored data, quantile functions with ![]() close to 1 may not be identifiable due to censorship. In our similations, we consider
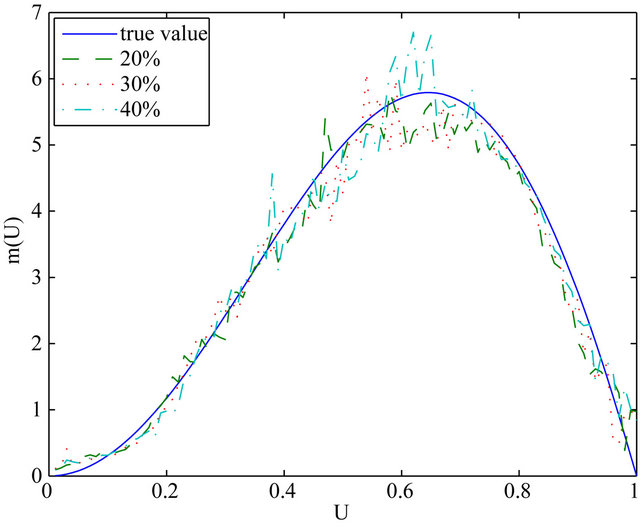
close to 1 may not be identifiable due to censorship. In our similations, we consider 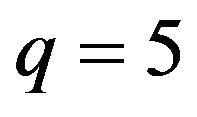 for LCQR and LCQRC estimators. The means and standard deviations of MADE, MSE, RMADE and RMSE are respectively reported in Table 1 and Table 2. From Tables 1 and 2, we can make the following observations: the performance of proposal method is better than that of LCRQ and NQRC. Moreover, LCQRC estimators are much more accurate when sample sizes increase. Figure 1 summarize the Curve estimates for three censoring rates of 20%, 30% and 40% with different sample sizes. It shows that the performance of LCQRC is very close to the true value.
for LCQR and LCQRC estimators. The means and standard deviations of MADE, MSE, RMADE and RMSE are respectively reported in Table 1 and Table 2. From Tables 1 and 2, we can make the following observations: the performance of proposal method is better than that of LCRQ and NQRC. Moreover, LCQRC estimators are much more accurate when sample sizes increase. Figure 1 summarize the Curve estimates for three censoring rates of 20%, 30% and 40% with different sample sizes. It shows that the performance of LCQRC is very close to the true value.
3.2. Example 2
It is necessary to investigate the effect of heteroscedastic errors. The observations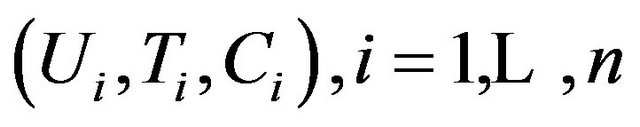 , are generated from following model
, are generated from following model
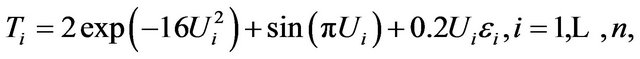
where 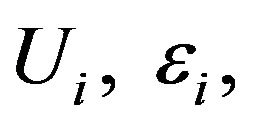 and
and 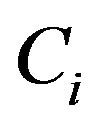 are generated following the same way as in Example 1. The means and standard deviations of MADE, MSE, RMADE and RMSE are respectively reported in Table 3 and Table 4. The
are generated following the same way as in Example 1. The means and standard deviations of MADE, MSE, RMADE and RMSE are respectively reported in Table 3 and Table 4. The
Table 1. Simulation results of 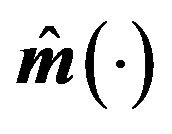 with n = 100 for Example 1.
with n = 100 for Example 1.
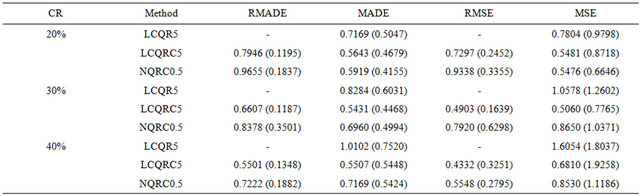
Table 2. Simulation results of 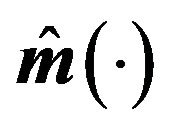 with n = 200 for Example 1.
with n = 200 for Example 1.
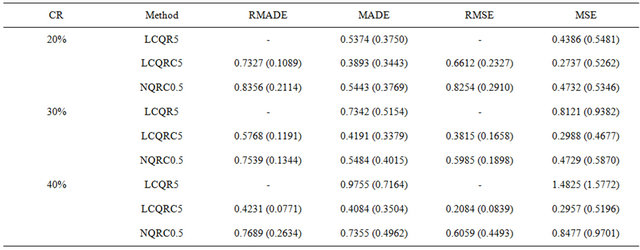
Table 3. Simulation results of  with n = 100 for Example 2.
with n = 100 for Example 2.

Table 4. Simulation results of  with n = 200 for Example 2.
with n = 200 for Example 2.
performance of LCQRC is presented in Figure 2. The results of Example 1 and Example 2 show very similar messages.
3.3. Example 3
As an illustration, we now apply the proposed LCQRC to the lung cancer data. The data contain 228 observations on ten variables. The censoring percentage is 27%, so the estimators are expected to perform well. More details about the study can be found in [11], and the dataset is included in the R package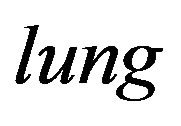 . We are interested in estimating the conditional of survival time (in days) given age (in years). Here, we use model (1) to fit the lung cancer data, where
. We are interested in estimating the conditional of survival time (in days) given age (in years). Here, we use model (1) to fit the lung cancer data, where ![]() is the
is the 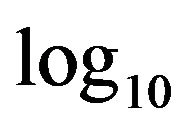 (survival time) and U is the age/100. To evaluate the performance of our estimator. Two distance measures were approximatedthe first one the mean absolute deviation error
(survival time) and U is the age/100. To evaluate the performance of our estimator. Two distance measures were approximatedthe first one the mean absolute deviation error
 given by
given by , and the second one the mean squared error
, and the second one the mean squared error 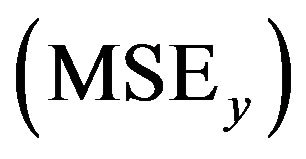 defined as
defined as
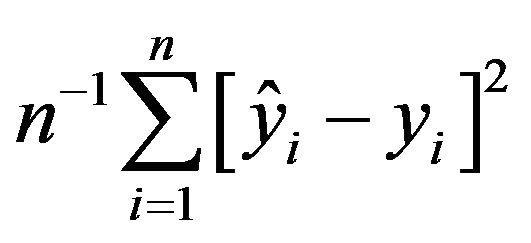 , where
, where . Furthermore, we define the rate of
. Furthermore, we define the rate of 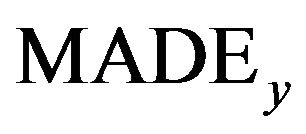 and
and 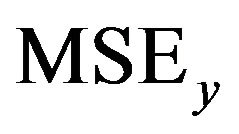 which are
which are
 and
and
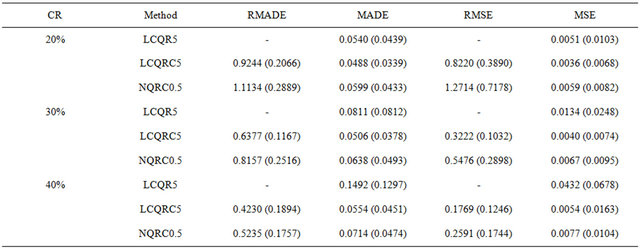
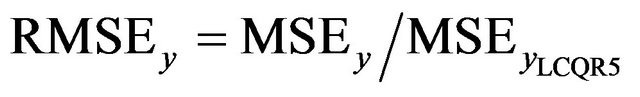 . Next, we report and compare results with LCQR and NQRC for estimating the survival time. The simulation results for the LCQR, LCQRC and NQRC are given in Table 5. It shows that LCQRC is better than that of LCRQ and NQRC. Figure 3 summarize the simulation results for LCQRC5. It
. Next, we report and compare results with LCQR and NQRC for estimating the survival time. The simulation results for the LCQR, LCQRC and NQRC are given in Table 5. It shows that LCQRC is better than that of LCRQ and NQRC. Figure 3 summarize the simulation results for LCQRC5. It
 (a)
(a)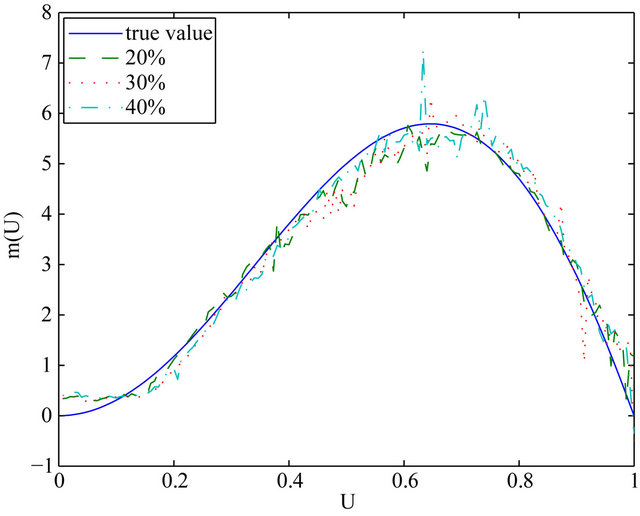 (b)
(b)
Figure 1. Curve estimates of 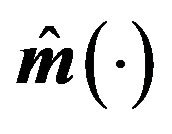 for Example 1. (a) n = 100; (b) n = 200.
for Example 1. (a) n = 100; (b) n = 200.
 (a)
(a) (b)
(b)
Figure 2. Curve estimates of 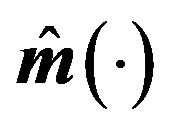 for Example 2. (a) n = 100; (b) n = 200.
for Example 2. (a) n = 100; (b) n = 200.
Table 5. Simulation results of  for lung cancer data.
for lung cancer data.
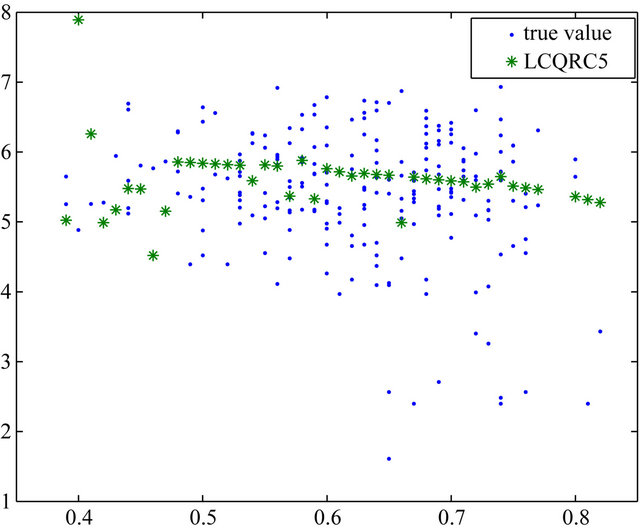
Figure 3. Curve estimates for lung cancer data.
shows that the proposal is valid.
4. Conclusion
In this work, we have focused on the LCQR for nonparametric model with censored data and its nice theoretical properties have been proven. The proposed approaches are demonstrated by simulation examples and real data applications. In addition, we believe the method can be extended to varying coefficient model (see [7]).
REFERENCES
- J. L. Powell, “Least Absolute Deviations Estimation for the Censored Regression Model,” Journal of Econometrics, Vol. 25, No. 3, 1984, pp. 303-325. doi:10.1016/0304-4076(84)90004-6
- S. Portnoy, “Censored Regression Quantiles,” Journal of the American Statistical Association, Vol. 98, No. 464, 2003, pp. 1001-1012. doi:10.1198/016214503000000954
- L. Peng and Y. Huang, “Survival Analysis with Quantile Regression Models,” Journal of the American Statistical Association, Vol. 103, No. 482, 2008, pp. 637-649. doi:10.1198/016214508000000355
- H. J. Wang and L. Wang, “Locally Weighted Censored Quantile Regression,” Journal of the American Statistical Association, Vol. 104, No. 478, 2009, pp. 1117-1128. doi:10.1198/jasa.2009.tm08230
- H. Zou and M. Yuan, “Composite Quantile Regression and the Oracle Model Selection Theory,” Annals of Statistics, Vol. 36, No. 3, 2008, pp. 1108-1126. doi:10.1214/07-AOS507
- B. Kai, R. Li and H. Zou, “Local Composite Quantile Regression Smoothing: An Efficient and Safe Alternative to Local Polynomial Regression,” Journal of the Royal Statistical Society, Series B, Vol. 72, No. 1, 2010, pp. 49- 69. doi:10.1111/j.1467-9868.2009.00725.x
- B. Kai, R. Li and H. Zou, “New Efficient Estimation and Variable Selection Methods for Semiparametric VaryingCoefficient Partially Linear Models,” Annals of Statistics, Vol. 39, No. 1, 2011, pp. 305-332. doi:10.1214/10-AOS842
- R. Jiang, Z. G. Zhou, W. M. Qian and W. Q. Shao, “Single-Index Composite Quantile Regression,” Journal of the Korean Statistical Society, Vol. 3, No. 3, 2012, pp. 323-332. doi:10.1016/j.jkss.2011.11.001
- R. Jiang, W. M. Qian and Z. G. Zhou, “Variable Selection and Coefficient Estimation via Composite Quantile Regression with Randomly Censored Data,” Statistics & Probability Letters, Vol. 2, No. 2, 2012, pp. 308-317. doi:10.1016/j.spl.2011.10.017
- A. Gannoun, J. Saracco, A. Yuan and G. Bonney, “NonParametric Quantile Regression with Censored Data,” Scandinavian Journal of Statistics, Vol. 32, No. 4, 2005, pp. 527-550. doi:10.1111/j.1467-9469.2005.00456.x
- C. L. Loprinzi, et al., “Prospective Evaluation of Prognostic Variables from Patient-Completed Questionnaires. North Central Cancer Treatment Group,” Journal of Clinical Oncology, Vol. 12, No. 3, 1994, pp. 601-607.
- W. Gonzalez-Manteiga and C. Cadarso-Suarez, “Asymptotic Properties of a Generalized Kaplan-Meier Estimator with Some Applications,” Journal of Nonparametric Statistics, Vol. 4, No. 1, 1994, pp. 65-78. doi:10.1080/10485259408832601
- K. Knight, “Limiting Distributions for L1 Regression Estimators under General Conditions,” Annals of Statistics, Vol. 26, No. 2, 1998, pp. 755-770. doi:10.1214/aos/1028144858
Appendix
Lemma 1. Assume assumption A1 hold. Then

where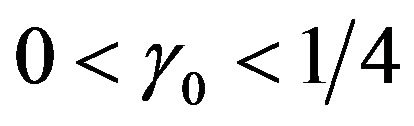 .
.
Proof. This follows directly from theorem 2.1 of [12].
Proof of Theorem 1 Let
 ,
,
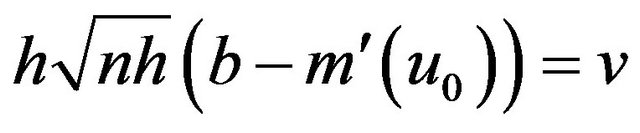 ,
, 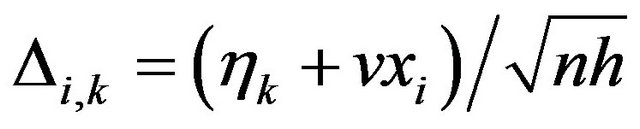 ,
,
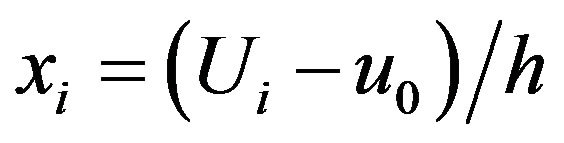 ,
,

Then 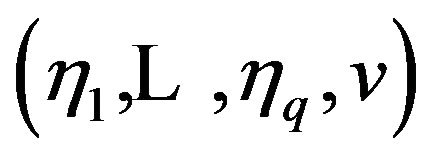 is the minimizer of the following criterion:
is the minimizer of the following criterion:
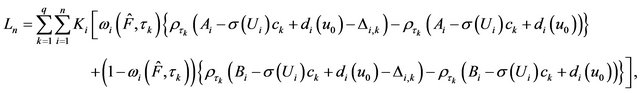
where 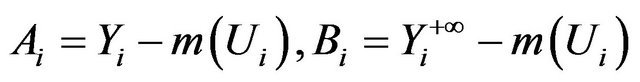 and
and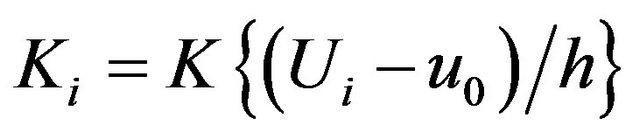 . To apply the identity ([13])
. To apply the identity ([13])
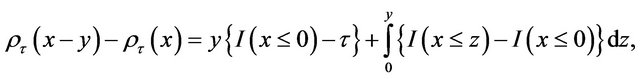
we have
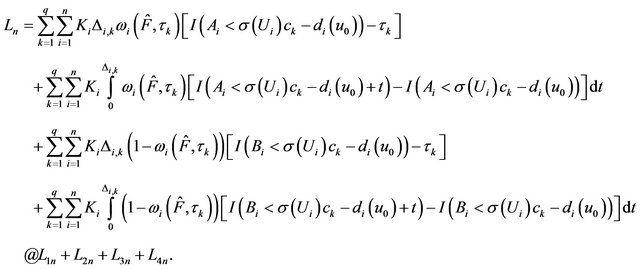
Since  is any value sufficiently large to exceed all
is any value sufficiently large to exceed all ,
, 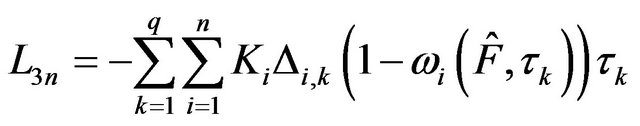 and
and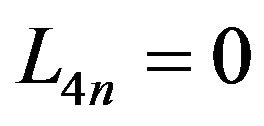 , then
, then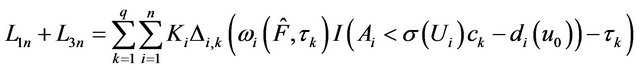 .
.
Denote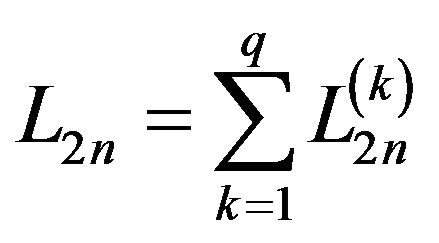 , where
, where
 .
.
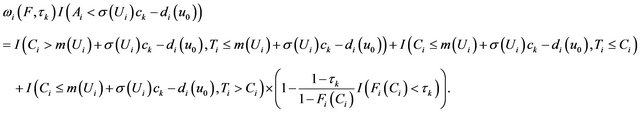
By the conditional independence of ![]() and
and  given
given , we have
, we have

Therefore,
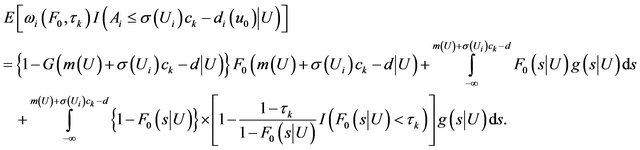
By Lemma 1, we have
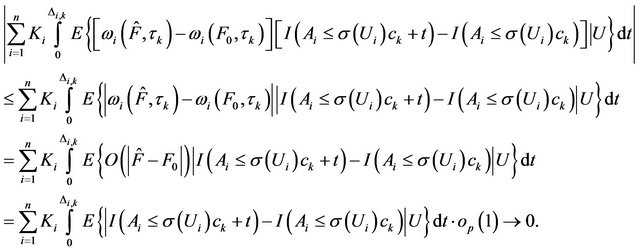
Then, we can obtain
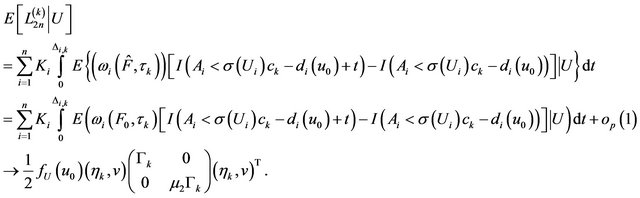
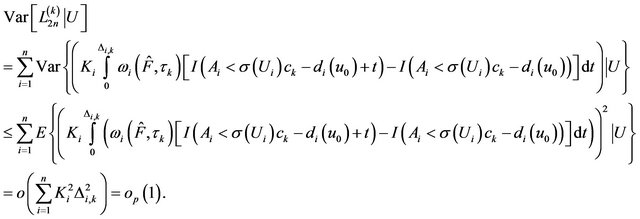
So, we can obtain , then
, then
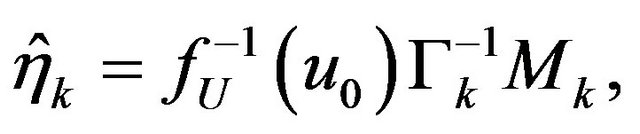
where
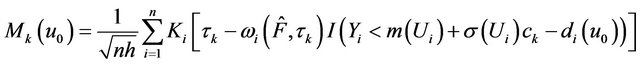 .
.
Note that the error is symmetric, thus , then it follows that
, then it follows that

Since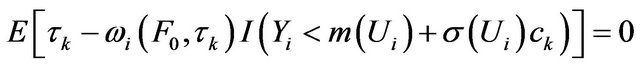 , then
, then
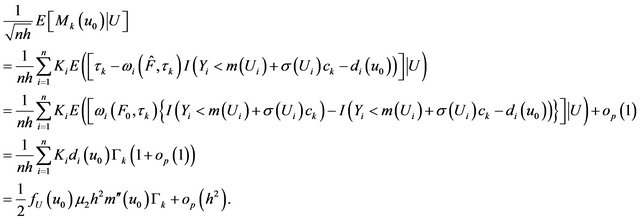
So, we can obtain
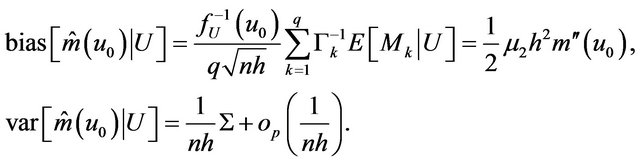
This completes the proof.

