Open Journal of Physical Chemistry
Vol.07 No.01(2017), Article ID:74390,17 pages
10.4236/ojpc.2017.71002
A Molecular Description of Superconductivity of Sulfur Hydride and Related Systems under High-Pressure Conditions
Henk M. Buck
Kasteel Twikkelerf 94, Tilburg, The Netherlands

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: January 4, 2017; Accepted: February 24, 2017; Published: February 27, 2017
ABSTRACT
It has been shown that the recently discovered sulfur trihydride (H3S) can be considered as a superconductor with a transition temperature Tc of 203 Kelvin (K) at 155 GigaPascals (GPa). This is the highest Tc value reported for any superconductor. The established superconductivity occurs via the formation of a molecular system with sulfur atoms arranged on a body-centered cubic lattice. It has been generally accepted that the high Tc value is the result of an efficient electron-phonon interaction. The responsible substance formed by H2S under high pressure, may be considered as a compound with H3S stoichiometry creating an impressive network with hydrogens. We will focus on the hydrogen bonding between sulfur and hydrogens demonstrating a symmetrical arrangement. The geometry of the individual radical compound in relation to corresponding systems will be discussed. Ab initio calculations based on a linear three-center two-, three- and four-electron type of bonding clearly visualized in combination with the dynamics of the Van’t Hoff concept, as described by us in various papers, give a good description of this exclusive network. We also discuss the superconductivity of related phosphorus hydrides and focus on the stability and geometrical differences with respect to the H3S system. These differences are significant, demonstrating the diversity in various structures in showing superconductivity.
Keywords:
Super Conductivity, High-Pressure Networks, Proton Bonding, Configurational Transitions in Extended Systems

1. Introduction
Errea et al. [1] demonstrated a quantum hydrogen-bond symmetrization for the recently discovered superconductivity of sulfur trihydride (H3S) by Drozdof et al. [2] . With a transition temperature (Tc) of 203 Kelvin (K) at 155 GigaPascals (GPa), it is the highest Tc value for this moment.
In fact there are two competing crystal structures, indicated as R3m and 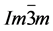 phases corresponding without symmetrization, i.e. a covalent S-H and a longer S∙∙∙H bond, and with symmetrization for equal bonds, respectively. In Figure 1, an impression is given (abstracted from Figure 1 [1] ) for the symmetrical arrangement. X-ray diffraction confirms the H3S stoichiometry and the sulfur lattice sites [3] [4] [5] [6] [7] . The supposed geometric difference between the S-H bond lengths between the two phases could not be experimentally demonstrated.
phases corresponding without symmetrization, i.e. a covalent S-H and a longer S∙∙∙H bond, and with symmetrization for equal bonds, respectively. In Figure 1, an impression is given (abstracted from Figure 1 [1] ) for the symmetrical arrangement. X-ray diffraction confirms the H3S stoichiometry and the sulfur lattice sites [3] [4] [5] [6] [7] . The supposed geometric difference between the S-H bond lengths between the two phases could not be experimentally demonstrated.
The hydrogen atom position is difficult to detect with X-ray diffraction even with single-crystal experiments. This aspect is strengthened by proton-like networks. A new method has been very recently demonstrated [8] .
In order to make a difference between these types of bonds, we used the classical convention of covalent and hydrogen bonding. With the latter bonding the electrostatic interaction delivers an important contribution through the proton-like arrangement. The fundamental role of hydrogen in (bio)physical chemical interactive sites will be explained and discussed on the basis of several examples in combination with related systems. Attention will be given at conformational changes in extended covalent-bonding systems.
From the DFT calculations, Errea et al. concluded that the structure corresponding with equal sulfur-hydrogen bond distances is the favored configuration for the superconductivity [1] . It is expected, based on experiments of Drozdov et al., that superconductivity at room temperature is possible for other hydrogen-rich systems if the quantum motion of the hydrogen affects the stability of the hydrogen chemical bonding and the electron-phonon coupling [2] .
Figure 1. Crystal structures of the 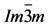 phase in which sulfur is surrounded by hydrogens with equal S-H distances. For the expected variations in the bond length, illustrating the differences in the competing phases, we refer to the text.
phase in which sulfur is surrounded by hydrogens with equal S-H distances. For the expected variations in the bond length, illustrating the differences in the competing phases, we refer to the text.
We also discussed the superconductivity of phosphorus hydride based on recent theoretical models of Shamp et al. [9] . An exclusive arrangement of the phosphorus atoms drew our attention.
From experiments based on pressure-induced decomposition of solid H2S, it is clear that under the high-pressure conditions a range of decompositions is possible mostly resulting in the favored H3S configuration. We discuss the geometry of the individual H3S radical in comparison with its corresponding cation. The differences are obvious.
Symmetry changes under high-pressure conditions were among others noticed by Edwards et al. concerning the pressure- and/or temperature-induced coordination change of boron in a borosilicate glass with high pressure 11B solid- state NMR spectroscopy in combination with ab initio calculations [10] . The results indicate a deformation of the B(OH)3 planar triangle into a trigonal pyramid that can be considered as the intermediate for the tetrahedral boron configuration. This geometrical change is of special interest as it corresponds with our original description based on Van’t Hoff modeling for the tetrahedral change of carbon in e.g. CH3X by substitution of X with nucleophiles via a trigonal bipyramidal state, in which the transferred carbon may be described as a methyl planar triangle cation [11] . Ab initio calculations based on a linear three- center two-, three- and four-electron type of bonding clearly portrayed in combination with the dynamics of the Van’t Hoff concept, as described by us in various papers, give a good description of the exclusivity of the network in its role as superconducting system. For this specific hydrogen symmetrization we briefly summarize the dynamics of the Van’t Hoff model. This process is based on the transition of a regular tetrahedron in which the interstitial carbon changes its position from tetrahedral into a trigonal bipyramidal configuration. It resembles a nucleophilic halogen (X−) addition-substitution reaction based on the SN2 profile. The identity reaction of X− + CH3X starts with a tetravalent carbon C(IV) and proceeds via a pentavalent carbon C(V) with (mirror)carbon inversion. This model description can be converted in a number of equations. With 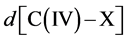 the bond distance of C-X in the tetrahedral configuration, with
the bond distance of C-X in the tetrahedral configuration, with 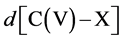 the bond distance of C-X in the pentavalent state, and the tetrahedral angle θ, the following characteristics can be given [11] [12] :
the bond distance of C-X in the pentavalent state, and the tetrahedral angle θ, the following characteristics can be given [11] [12] :
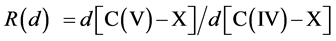 and
and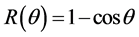 ,
,
combination gives:
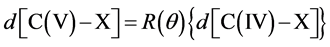
For comparison we give the ab initio results using relativistic DFT at the ZORA-OLYP/TZ2P level for 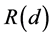 - and the corresponding
- and the corresponding 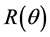 -values in parentheses. For X = F: 1.332 (1.322); Cl: 1.318 (1.319); Br: 1.281 (1.304) and I: 1.261 (1.319). The R-values are in good correspondence with the expectation value of 1.333, using the Van’t Hoff tetrahedral angle of 109.47˚.
-values in parentheses. For X = F: 1.332 (1.322); Cl: 1.318 (1.319); Br: 1.281 (1.304) and I: 1.261 (1.319). The R-values are in good correspondence with the expectation value of 1.333, using the Van’t Hoff tetrahedral angle of 109.47˚.
In our opinion in the SH network the proton plays a unique role involving a three-center four-electron bonding. For various combinations we also introduced the value R(n), in which n is the number of electrons in the intermediate state of the three-center bonding [11] [12] [13] :
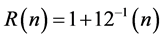
resulting for n equals 4, 3, and 2 in 1.333, 1.250, and 1.167, respectively. Thus we can for instance replace the methyl cation by protons, halonium ions, etc. As an illustration the R(d)- and R(n)-values are given using NPA charges and the optimized C-H bond lengths from Keeffe et al. [14] and Gronert et al. [15] concerning the identity proton transfer between Y-C-H and Y-C− with the R(n)- value in parentheses. For CH3C CH: 1.320 (1.280); CH3CH=CHH: 1.312 (1.297); H2C=C=CHH: 1.288 (1.289); CH3CH2CH2H: 1.314 (1.309); O2NCH2H: 1.278 (1.244); CH3SO2CH2H: 1.308 (1.325). From these results it has been clearly demonstrated that the values for R(d) and R(n) are comparable and close to 1.333. In the case of O2NCH2H conjugation with the nitro group lowers the R- value. The number of electrons in the intermediate state decreases from 4 (ideal) to 2.931. Interestingly, in CH3SO2CH2H the conjugation is completely suppressed by the sulfone group as illustrated with the corresponding value of 3.896 electrons in the intermediate state. It is clear that the difference between the displacement of the proton and the methyl carbenium ion on the principal reaction coordinate is of minor importance for the description of the corresponding transition intermediates with respect to their R-values.
CH: 1.320 (1.280); CH3CH=CHH: 1.312 (1.297); H2C=C=CHH: 1.288 (1.289); CH3CH2CH2H: 1.314 (1.309); O2NCH2H: 1.278 (1.244); CH3SO2CH2H: 1.308 (1.325). From these results it has been clearly demonstrated that the values for R(d) and R(n) are comparable and close to 1.333. In the case of O2NCH2H conjugation with the nitro group lowers the R- value. The number of electrons in the intermediate state decreases from 4 (ideal) to 2.931. Interestingly, in CH3SO2CH2H the conjugation is completely suppressed by the sulfone group as illustrated with the corresponding value of 3.896 electrons in the intermediate state. It is clear that the difference between the displacement of the proton and the methyl carbenium ion on the principal reaction coordinate is of minor importance for the description of the corresponding transition intermediates with respect to their R-values.
In all these cases for proton dynamics we are dealing with hydrogen-bond symmetrization in their transition intermediates. Energy minima has been calculated based on cage compounds with geometrical variation. However, these compounds show under crystalline conditions proton localization between nitrogens as exclusive biophysical sites with short N-H and long N∙∙∙H bonds. These distances correspond (or differ) with (from) the hydrogen-bridge distances in DNA in dependence of the length of the N-N distance determined by the geometrical constraints of rigid frameworks as clearly demonstrated by Gunbas and Mascal [16] . The short-long distances 1.069Å and 1.733Å, correspond with the hydrogen bonding in the DNA duplex and similar systems. One of the fascinating examples in which this type of hydrogen bonding is correlated with intermolecular complexation, demonstrating an exceptional dielectric response, has been found in the disproportionation of pyrazine-HClO4 in the N-H∙∙∙N hydrogen-bonded complexes. In all these cases the distance between the nitrogen sites is in excellent correspondence with the Van’t Hoff concept [17] .
For the dynamic displacement of the methyl cation no trigonal bipyramidal configuration could be synthesized with the characteristic value R(d) = 1.333. This intermediate type of configuration for SN2 like reactions was approached by Yamashita et al. [18] using artificial model systems. In this study they describe the synthesis and X-ray diffraction of ten-electron penta-coordinate carbons bearing an anthracene skeleton with two apical OCH3 substituents at the 1,8 positions of anthracene linked with -C+(OCH3)2 at the 9-position. The X-ray showed a trigonal bipyramid with apical distances of 2.44Å, i.e. R(d) = 1.66 (tetravalent value is 1.47Å). Changing carbon by boron as -B(OCH3)2 resulted in apical distances of 2.44Å with R(d) = 1.44 (tetravalent value is 1.69Å). The fact that CH3+ is isoelectronic with BH3, both elements are consecutive second-period elements, clearly demonstrates the ability for the formation of a pentavalent intermediate. Electronegative substituents promote the electrophilicity of both elements as was shown for boron. Replacing -B(OCH3)2 by -BF2 resulted in an experimental value of R(d) = 1.36 (tetravalent value is 1.69Å). DFT calculations gave 1.33. The latter configuration looks like a frozen intermediate state, originated by its rigid framework. This is a cage compound in which the migrating particle is already placed on the vital position of the principal reaction coordinate for the linear three-center four-electron transition state. Furthermore, it is of interest that the tetrahedral configuration under the conditions of the predestinated geometry reflects the pre- and post-geometry of the identity nucleophilic reactions as formulated by the identity reaction of X− + CH3X, resulting in short (C-X) and long (C∙∙∙X) bonds as d and 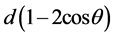 or 1.67 d, respectively. Within the same framework this aspect can be found back in which the electrophile is frozen in a tetrahedral configuration for -BCl2 (-BF2 gives the pentavalent state, vide supra). The X-ray data give for the short and long bond distance DFT values of 1.77Å and 2.77Å with a ratio of 1.56. Summarizing, the geometric switch is the consequence of change in electronegativity from -BCl2 into -BF2 [12] [19] .
or 1.67 d, respectively. Within the same framework this aspect can be found back in which the electrophile is frozen in a tetrahedral configuration for -BCl2 (-BF2 gives the pentavalent state, vide supra). The X-ray data give for the short and long bond distance DFT values of 1.77Å and 2.77Å with a ratio of 1.56. Summarizing, the geometric switch is the consequence of change in electronegativity from -BCl2 into -BF2 [12] [19] .
Trigonal bipyramids as pentavalent configurations are mostly found for silicon, phosphorus and sulfur with R(d)-values (much) smaller than the critical value of 1.333. In these cases also the influence of the substituents of the central elements has been clearly demonstrated in the energy profile focused on the intermediate structure [19] .
With the composition of equations as given before we can describe the three- center four-, three- and two-electron type of bonding under conditions of linearity. However, there are examples using ab initio calculations showing deviation from linearity. As an example we mention the differences for identity reactions for H3CH, proton-like with its anion (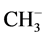 ), hydrogen atom-like with its radical (CH3∙), and hydride-like with its cation (
), hydrogen atom-like with its radical (CH3∙), and hydride-like with its cation (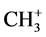 ) or an activated carbonyl bond or otherwise activated [12] . The C-H-C angles for these combinations are 180˚, 180˚, and 103.2˚, respectively. Substitution of an alkyl substituent in the latter case results in an increase of the C-H-C angle from methyl, ethyl, isopropyl to t-butyl in the order of 103.2˚, 122.4˚, 165.8˚, 180˚. We focus specifically on the C-H-C intermediate in the transfer of their electrons. The dynamics for the four-electron transition results in a mirror-imaged symmetry. Although the latter geometric configuration as intermediate state is closely related to SN2, shown for addition-substitution reactions under inversion, we are dealing in the latter case with a direct addition on the substrate molecule and not with an activated one as in the exchange reactions. Generally this difference has no impact on the distances following the principle reaction coordinate, unless another reaction mode is selected. As a deviating and well-known example we mention H+ + CH4 resulting in
) or an activated carbonyl bond or otherwise activated [12] . The C-H-C angles for these combinations are 180˚, 180˚, and 103.2˚, respectively. Substitution of an alkyl substituent in the latter case results in an increase of the C-H-C angle from methyl, ethyl, isopropyl to t-butyl in the order of 103.2˚, 122.4˚, 165.8˚, 180˚. We focus specifically on the C-H-C intermediate in the transfer of their electrons. The dynamics for the four-electron transition results in a mirror-imaged symmetry. Although the latter geometric configuration as intermediate state is closely related to SN2, shown for addition-substitution reactions under inversion, we are dealing in the latter case with a direct addition on the substrate molecule and not with an activated one as in the exchange reactions. Generally this difference has no impact on the distances following the principle reaction coordinate, unless another reaction mode is selected. As a deviating and well-known example we mention H+ + CH4 resulting in 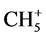 with Cs instead of D3h symmetry. There are various examples, most of them may be solved by knowing the structure of the product formed specifically for reactions involving inter and intra electron accommodation [20] .
with Cs instead of D3h symmetry. There are various examples, most of them may be solved by knowing the structure of the product formed specifically for reactions involving inter and intra electron accommodation [20] .
2. Results and Discussions
2.1. The Pressure (GPa) as a Function of the Lattice Parameter(a) for the Symmetric H3S Structure
Values for the pressure corresponding with the lattice parameters were offered by Errea et al. [1] . These numbers given in Table 1, are based on calculated values for the pressure for each lattice parameter. They mentioned that the pressure (in GPa) for each lattice parameter (a, in Å) is calculated within the PBE (Perdew-Burke-Ernzerhof) approach and including anharmonicity for the latter vibrations [1] . These results are elaborated under Table 2 and summarized for the pressure as function of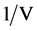 , in which V corresponds with a3. Each hydrogen atom resides midway between two sulfur atoms as part of a cubic symmetry. The apparent lattice parameter approaching zero-pressure condition has been obtained by extrapolation as shown in Figure 2. From this approach we were able to obtain additional control for the expected change in S-H bond distance. The numbers of Errea et al. given in Table 1, are the calculated values for the pressure for each lattice parameter, vide supra.
, in which V corresponds with a3. Each hydrogen atom resides midway between two sulfur atoms as part of a cubic symmetry. The apparent lattice parameter approaching zero-pressure condition has been obtained by extrapolation as shown in Figure 2. From this approach we were able to obtain additional control for the expected change in S-H bond distance. The numbers of Errea et al. given in Table 1, are the calculated values for the pressure for each lattice parameter, vide supra.
Table 1. Calculated value for the pressure P(GPa) for each lattice parameter a(Å).
aValues of pressure (P) in GPa. bValues of lattice parameter (a) in Å.
Table 2. Calculated values of the pressure P(GPa) for each lattice parameter a(Å), the inverse of volume V(Å−3) and the bond distance d(Å) of the covalent S-H bond following the Van’t Hoff modela and the interrelated modelsb.
a,bThe bond distances are obtained from the a-values by multiplying with 2.667−1, 2.5−1, and 2.334−1, respectively, vide supra. cValues of 1/V for P approaching zero-pressure conditions, are obtained via extrapolation as visualized in Figure 2.
Figure 2. Relation between pressure (P) as function of 1/V (a−3 × 103, in Å−3). The linear function (blue) is part of the function (red) as derived from the numbers given by Errea et al., see Table 1. The extrapolated dotted line (blue) gives the zero-pressure value with 1/V = 26.084Å−3. The corresponding value for a = 3.37190Å resulting in dS-H = 1.26446Å.
The significance of our approach lies in the possibility that we might be able to get an impression of the compactness of the structure as realized by its cubic symmetry since it is often suggested that this cubic structure is very close to the R3m phase with covalently bonded S-H bonds in combination with longer S∙∙∙H bonds. Therefore the introduced dynamic model of Van’t Hoff is a realistic model for control of the a-values obtained under very stringent conditions resulting in superconductivity. Using this model description there will be a more pronounced discrimination in bond distances between the characterized phases. In fact these different geometries are clearly demonstrated (stabilized pentavalent and tetravalent boron complexes) as shown before [19] .
With the demonstrated coherence for the off-centering of the proton resulting in a ratio between the long and short SH bonds of a factor 1.667, it will be clear that the compactness of the structure as suggested will be strongly reduced in the R3m phase compared with the optimal symmetrization in the ideal cubic structure (this factor decreases in the order of 1.667, 1.500 to 1.334 for proton-, hydrogen atom-to hydride-like, respectively, demonstrating a regular decrease) [11] [12] [13] . We presume that for interrelated models under pressure there is a slightly distorted symmetry in order to accommodate the hydrogen network resulting in a decrease of bond distances. The latter aspect is shown in Table 2.
The relation for the 
From these findings it seems that the result of Table 2 and the corresponding Figure 2 focused on the S-H distance for approaching zero-pressure is in good correspondence with the regular bond distance (1.32Å - 1.35Å). In the absence of the specific symmetry as described for the hydrogen bonding in the superconducting H3S system we calculated with the Van’t Hoff model for the non- symmetric S-H∙∙∙S hydrogen bridge a distance (a) of 3.52Å - 3.60Å, composed of a short and long SH distance of 1.32Å, 2.20Å ? 1.35Å, 2.25Å, using the values of 1.32Å and 1.35Å for the regular SH distance. According to the model description the differences between short and long distances are maximal values. It is of interest to focus on the curve fitting in Figure 2. The curve manipulation demonstrates the specificity of the crystal structure enabling superconductivity. The loss of its superconductivity is depicted with the sigmoidal curve as shown in this Figure.
2.2. Superconduction of Corresponding Phosphorus Hydrides. Stability and Geometrical Differences
Hypervalent radicals as H3S have been shown to be meta-stable on the microsecond time scale when generated as partially deuterated species [23] . However, most of the research came from an ESR study of 31P-centered radicals. These radicals can be described as phosphoranyl radicals with the configurations TBP- e, TBP-a, and σ* in which TBP stands for trigonal bipyramid with the odd electron in one of the equatorial and apical positions, respectively [24] . The latter configuration deals with the singly occupied molecular orbital (SOMO) if one of the ligands of the four-coordinate phosphorus is stabilized by an electronegative substituent. The generation of the phosphorus-centered radicals has been carried out under various conditions. It has been clearly demonstrated e.g., that the microenvironment of the radical precursor has a great influence on the formation of radiogenic radicals [25] . These radicals may be considered as “stable”. On the other hand many simple PH radicals are described under specific matrix conditions.
The TBP-e and TBP-a configurations for the H3S radical seem realistic because of the separation of the sulfur lone-pair and the odd electron. However, the e, e bond angles ask for an increase of about 25˚. In the H3S cation the sulfur atom has C3v symmetry with bond angles of 94.2˚ and a S-H distance of 1.35Å, values corresponding with ab initio results. Generally, the distance is varying from 1.32Å - 1.35Å (the sum of the covalent radii is 1.32Å) [26] . Accommodating the odd electron for the formation of the H3S radical with conservation of a tetrahedral geometry is very unlikely in the absence of an electronegative ligand. Under these conditions a fast dissociation takes place into hydrogen and H2S. In fact the problem must be reduced to the most effective location of the unpaired electron on sulfur. We suggest the contribution of a sulfur 4s orbital participation. This approach involves that the H3S radical can be considered as a pseudo alkalimetal (potassium). This special 4s electron may play a specific role in the electron-phonon contribution of the crystal lattice in the superconducting sulfide system consisting of the sulfur atoms arranged on a body-centered cubic lattice.
The suggestion of the 4s contribution finds its origin in an article describing the electron-driven proton transfer from hydrogen chloride to ammonia. An example for a system which might be considered as an outer complex. Eustis et al. describe this interaction as a hydrogen-bonded complex H3N∙∙∙HCl that via an excess electron is converted into the ionic ammonium chloride in which NH4 can be considered as a Rydberg radical with the odd electron in the 3s orbital, resulting in a pseudo alkalimetal (sodium) electron distribution [27] . For the ionization potential of the NH4 radical 5.08 eV was calculated, a value corresponding with the ionization potential of sodium (exp. value 5.14 eV). We discussed the overall electron-induced proton transfer from the gas phase proton affinities, clearly demonstrating the endothermic character of this proton transfer [19] . The difference in proton affinity is 5.47 eV in favor of Cl−. Nevertheless the preference for an outer complex via hydrogen bridging will be realized by the interaction of the resulting (partly) charged species. For the electron binding energy of the excess electron a value of about 0.51 eV was calculated, corresponding with the results of anion photoelectron spectroscopy (0.54 eV). The decrease in comparison with the ionization potential is caused by the fact that the unpaired electron is polarized and destabilized by the nearby Cl−.
In our opinion the 4s electron of a H3S radical may play a specific role in the electron-phonon contribution of the crystal lattice. It is possible that the superconduction temperature is tuned by the introduction of electrons through a specific orientation of the H3S radical on the surface of the hydrogen sulfide system [28] . Focusing on specific physical chemical properties in the hydrogen network, we hypothesize that the proton-like location in the hydrogen sulfide system promotes an interplay with the 4s electron of the H3S radicals.
In fact a part of this consideration has been also described in an essay of Steele on Approaching an Ambient Superconductor (2005). In this work a synthesis is proposed for the 1,3,5-trithiabenzenium monocation with two electrons located in sulfur 4s AOs. According to Steele’s theoretical and experimental approach, the trithiabenzenium cation may be considered as a molecular metal demonstrating superconductivity. The preferred location for the sulfur 4s AO orbital has been discussed in detail.
In order to demonstrate the unique behavior of H3S as superconductor, we will focus attention on the recent theoretical research of Shamp et al. [9] . They used evolutionary algorithms in combination with DFT calculations to demonstrate stable hydrides derived from the decomposition of phosphine indicated as PH1-6. The non-specifity is clearly demonstrated by the three metallic PH2 phases demonstrating superconductivity between 100 and 200 GPa. One of these phases is the complex system (P5H10) which is of interest from a structural as well as from a chemical point of view. It has 

Our interest was focused on this particular geometry in comparison with a more traditional description. An interesting aspect is the charge distribution in P5H10.
In fact from a naive view that we are dealing with an overall +3.0 charge (three alternating “phosphonium” tetravalent locations) that must be reduced to zero by the introduction of an equal polarity at hydrogen of each P-H bond, remains rather misleading (compare with the aforementioned results as calculated for 100 and 150 GPa). Via reallocation we obtained for the qP values corresponding with 150 GPa: +0.955 (P in PH3-), +0.235 (P in -PH-), and +0.620 (P in -PH2-) in combination with a qH (av.) = −0.30. However, it is to be expected that the polarity following this procedure is on the high side (for a single covalent P-H bond we estimate a value of −0.15).
However, the P atom in PH3- is octahedrally coordinated with three phosphorus atoms and one hydrogen in equatorial position and two hydrogens in axial position. The P atom in -PH- has a trigonal bipyramidal configuration with two phosphorus atoms in apical positions and two phosphorus and one hydrogen in equatorial position explaining the H3P-PH-PH2 angle of about 130˚ (idealized configuration 120˚) as visualized in Figure 3, corresponding with a non- bonding P∙∙∙P distance of 3.9Å - 4.0Å. This value corresponds with the Van der Waals interaction of 3.9Å. The P atom in -PH2- has an octahedral geometry with four phosphorus atoms in equatorial and two hydrogens in axial position. The
Figure 3. Super cell of the 100 GPa 5FU/C2/m structure. A presentation of the coordination (see text) and the arrangement of the phosphorus atoms in PH3-PH-PH2-PH-PH3. The phosphorus atoms are orange and the hydrogen atoms white. The figure is abstracted from Figure 3 [9] .
geometrical refinement along the phosphorus atoms results in an inversion center of symmetry. This is visualized in Figure 3. Many in(organic) phosphorus compounds are well-known with a trigonal bipyramidal and octahedrally coordination, simplfied as PX5 and 
It is of interest to notice that the average P-P distance is 2.18Å which corresponds with a distance under normal conditions. The P-H distances vary between 1.430Å and 1.444Å, close to the normal value of 1.437Å. The absence of specific changes in bond lengths and the variation in geometric configurations results in a decrease of the Tc value in comparison with e.g. the highly symmetric H3S system.
Considering the structure in Figure 3 it remains still a problem to give a real representation with geometries for the P5H10 oligomer. The poly-radical structure as given by:
enables the possibility for the interaction profile with mono-radical (PH3- and -PH2-) and biradical (-PH-) fragments in the super cell. In relation to the afore mentioned description, this model also offer an explanation for the charge polarization in the P-H bonds via partial electron-donation of phosphorus to the P-H σ* bond as electron acceptor. It looks as an apparent conflicting pattern in the description of chemical bonding between low- and high-pressure chemistry.
Following the computational results it indicated that the superconductivity is a result of the structure assumed by the two-dimensional surface and that the mobile electron move within the two-dimensional layers, and along the P-P bonds. The same conclusion could be drawn for the other PH1-6 structures containing one-dimensional chains and two-dimensional sheets. The decrease in Tc value in comparison with H3S reflects in a more specific way the absence of P-H-P hydrogen bridges.
2.3. Role of Bond Symmetrization for a Specific Linear Three-Atom Arrangement as [N-X-N]+ with N Stands for Pyridinium and X for Hydrogen and Iodine. Comparison with the Geometry of Homonuclear Poly-Iodine Ions
It seems to us that the unexpected spin-off of hydrogen-bond symmetrization under high-pressure conditions deserves a broader view from a physical (bio) chemical standard. We focus on the nature of [N-X-N]+ bonds with X = hydrogen, because of its biochemical relevance, and iodine in relation to one of the fundamental aspects of nucleophilic SN2 substitution reactions. This arrangement will be also discussed in comparison with structures as homonuclear poly-iodine ions. The study of this kind of hydrogen and halogen bonding has been recently explored by the group of Erdélyi et al. [29] [30] [31] . For hydrogen the results show no essential difference compared with our results. With the ab initio results of this group we obtained the R(d)-values, vide supra, for I, Br, and Cl 1.100, 1.130, and 1.173 respectively. These values demonstrate the stability obtained via a symmetric halogen bonding. For I, an X-ray determination has been published with [(pyr)N-I-N(pyr)]+ distances which differ about 0.05Å from the theoretical values. For F we are dealing with an outer complex with R(d) = 2.573 missing the characteristic value of 1.667, related to the initial step. On the other hand, the calculated short-long distances for N-H∙∙∙N (1.069Å and 1.733Å), correspond with the latter value. Unstable symmetric N-H-N structures are obtained with values of 1.272 and 1.300 (these values are in agreement with the expectation value of 1.333). The value of 1.300 is obtained with a more rigid substrate in which the geometry of the pyridines is fixed with a N-N distance of 4.680Å. Surprisingly, the influence of the rigid structure has no influence on the nitrogen-halogen distances. The difference in the formation of a three-center four-electron bonding for halogen in comparison with hydrogen results in an exclusive configuration in which its transition occurs through the lone pair of nitrogen in pyridine on the activated halogen covalently attached to the positively charged nitrogen of the other pyridine within a trigonal bipyramid. The halogen has two apical bonds with both pyridines and three equatorial sites each containing two electrons. In the initial stage the halogen distributes the lone pairs conform a tetrahedral arrangement. This situation follows the classical SN2 reaction to its intermediate transition in which the tetrahedral configuration inverts via the trigonal bipyramidal configuration. The absence of fluorine can be understood by presuming that in its pseudo tetrahedral configuration the electron density of fluorine increases that deactivates the interaction with the other pyridine.
These findings are in good correspondence with a recent paper of Thanthiriwatte et al. based on the structure (angels (degrees) and distances (Å)) of halogen clusters anions related to the foregoing complexes [32] . We mention 



From the structures it is clear that 


Figure 4. The geometric structures of


overall charge is sum of all individual configurations, the calculated NBO charges demonstrate a (significant) degree of delocalization. The individual configurations can be considered as specific donor and acceptor markers with high and low energy profiles corresponding with the trigonal bipyramidal and the tetrahedral individuals. This aspect is shown with the NBO calculations.
These results are not limited to iodine. Similar (geometric) results are obtained for chlorine and bromine. Using R(d), we calculated as a stability indication for 


3. Conclusions
Recent investigations have demonstrated that hydrogen sulfide systems with H3S stoichiometry show superconductivity with a transition temperature of 203 K at 155 GPa.
A fascinating aspect is the position of the hydrogens in the network showing a symmetrical arrangement. The conclusion in the paper of Errea et al. is that considering the quantum vibrations of the atoms in the calculations of the Gibbs free energy, the configuration with symmetrized bonds is favored [1] . With the values for the pressure and the lattice parameter as given in Table 2, we were able with curve fitting as demonstrated in Figure 2, to obtain under “zero- pressure condition” the lattice parameter and the corresponding covalent sulfur-hydrogen distance. The value for the lattice parameter is 3.37190Å with a covalent S-H bond distance of 1.26446Å. The regular value for the bond distance is 1.32Å. The conversion values from the lattice parameters into the covalent bond distances were based on the SN2 profile illustrated as X− + CH3X. This model has been described in a number of papers. To the best of our knowledge, the symmetrical hydrogen bond distance between sulfur and hydrogen in the superconducting hydrogen sulfide system is one of the first stable examples of this unique hydrogen-bond symmetrization. It may be noticed that under high- pressure conditions symmetrization of the hydrogen bond in ice is realized indicating that the hydrogen-bonded protons initially located at asymmetric positions of the O-O separation will relocate to the symmetric midpoint, which transforms the system to the symmetric phase [34] . In addition, it is of interest to emphasize that curve fitting in Figure 2 demonstrates the specificity of the crystal structure enabling superconductivity. The loss of superconductivity is depicted with the sigmoidal curve. Demonstrating the unique behavior of H3S as superconductor, we gave attention to recent research of Shamp et al. [9] . They used evolutionary algorithms in combination with DFT calculations to select possible stable hydrides derived from the decomposition of phosphine indicated as PH1-6. The non-specificity is clearly demonstrated by the three metallic PH2 phases demonstrating super conductivity between 100 and 200 GPa. One of these phases is the complex system PH3-PH-PH2-PH-PH3(P5H10) which is of interest from a structural as well as from a chemical point of view. In fact there is no real agreement with the H3S system. In our opinion the difference between both systems is the absence of formal P-H-P hydrogen bridges. The unexpected spin-off of hydrogen-bond symmetrization under high-pressure conditions deserves a broader view from a physical (bio)chemical perspective. Finally, we focus on the nature of [N-X-N]+ bonds with X = hydrogen, because of its biochemical relevance, and iodine in relation to one of the fundamental aspects of nucleophilic substitution SN2 reactions. The results are discussed in comparison with structures as homonuclear poly-iodine ions.
Acknowledgements
I thank dr. Ion Errea of the Dosnostia International Physics Center of the University of the Basque Country giving the table with the lattice parameters as a function of pressure for the symmetric H3S structure and theoretical information. I thank dr. Máté Erdélyi of the Department of Chemistry and Molecular Biology of the Gothenburg University for giving experimental and theoretical information on the symmetric halogen bonding. I thank dr. Eva Zurek of the Department of Chemistry, State University of New York at Buffalo for valuable discussion on hydrides of phosphorus under high pressure. I thank my grandchildren Robin van Dorrestein and Martin Buck BSc for valuable technical assistance.
Cite this paper
Buck, H.M. (2017) A Molecular Description of Superconductivity of Sulfur Hydride and Related Systems under High-Pressure Conditions. Open Journal of Physical Chemistry, 7, 9-25. https://doi.org/10.4236/ojpc.2017.71002
References
- 1. Errea, I., Calandra, M., Pickard, C.J., Nelson, J.R., Needs, R.J., Li, Y., Liu, H., Zhang, Y., Ma, Y. and Mauri, F. (2016) Quantum Hydrogen-Bond Symmetrization in the Superconducting Hydrogen Sulfide System. Nature, 532, 81-84.
https://doi.org/10.1038/nature17175 - 2. Drozdov, A.P., Eremets, M.I., Troyan, I.A., Ksenofontov, V. and Shylin, S.I. (2015) Conventional Superconductivity at 203 Kelvin at High Pressures in the Sulfur Hydride System. Nature, 525, 73-76.
https://doi.org/10.1038/nature14964 - 3. Duan, D., Liu, Y., Tian, F., Li, D., Huang, X., Zhao, Z., Yu, H., Liu, B., Tian, W. and Cui, T. (2014) Pressure-Induced Metallization of Dense (H2S)2H2 with High-Tc Superconductivity. Scientific Reports, 4, 6968.
https://doi.org/10.1038/srep06968 - 4. Duan, D., Huang, X., Tian, F., Li, D., Yu, H., Liu, Y., Ma, Y., Liu, B. and Cui, T. (2015) Pressure-Induced Decomposition of Solid Hydrogen Sulfide. Physical Review B, 91, 180502.
https://doi.org/10.1103/physrevb.91.180502 - 5. Errea, I., Calandra, M., Pickard, C.J., Nelson, J.R., Needs, R.J., Li, Y., Liu, H., Zhang, Y., Ma, Y. and Mauri, F. (2015) High-Pressure Hydrogen Sulfide from First Principles: A Strongly Anharmonic Phonon-Mediated Superconductor. Physical Review Letters, 114, 157004.
https://doi.org/10.1103/physrevlett.114.157004 - 6. Li, Y., Wang, L., Liu, H., Zhang, Y., Hao, J., Pickard, C.J., Nelson, J.R., Needs, Li, W., Huang, Y., Errea, I. and Calandra, F. (2016) Dissociation Products and Structures of Solid H2S at Strong Compression. Physical Review B, 93, 020103(R).
https://doi.org/10.1103/PhysRevB.93.020103 - 7. Bernstein, N., Hellberg, C.S., Johannes, M.D., Mazin, I.I. and Mehl, M.J. (2015) What Superconducts in Sulfur Hydrides under Pressure and Why. Physical Review B, 91, 060511.
https://doi.org/10.1103/physrevb.91.060511 - 8. Palatinus, L., Brázda, P., Boullay, P., Perez, O., Kiementová, M., Petit, S., Eigner, V., Zaarour, M. and Mintova, S. (2017) Hydrogen Positions in Single Nanocrystals Revealed by Electron Diffraction. Science, 355, 166-169.
https://doi.org/10.1126/science.aak9652 - 9. Shamp, A., Terpstra, T., Bi, T., Falls, Z., Avery, P. and Zurek, E. (2016) Decomposition Products of Phosphine under Pressure: PH2 Stable and Superconducting? Journal of the American Chemical Society, 138, 1884-1892.
https://doi.org/10.1021/jacs.5b10180 - 10. Edwards, T., Endo, T., Walton, J.H. and Sen, S. (2014) Observation of the Transition State for Pressure-Induced BO3→ BO4 Conversion in Glass. Science, 343, 1027-1029.
https://doi.org/10.1126/science.1256224 - 11. Buck, H.M. (2015) Interconversion between Planar-Triangle, Trigonal-Pyramid and Tetrahedral Configurations of Boron (B(OH)3-B(OH)4﹣), Carbon (CH3+-CH3X) and for the Group 15 Elements as Nitrogen (NH3-NH4+). A Modelling Description with ab Initio Results and Pressure-Induced Experimental Evidence. Open Journal of Physical Chemistry, 5, 1-8.
https://doi.org/10.4236/ojpc.2015.51001 - 12. Buck, H.M. (2008) A Combined Experimental, Theoretical, and Van’t Hoff Model Study for Identity Methyl, Proton, Hydrogen Atom, and Hydride Exchange Reactions. Correlation with Three-Center Four-, Three-, and Two-Electron Systems. International Journal of Quantum Chemistry, 108, 1601-1614.
https://doi.org/10.1002/qua.21683 - 13. Buck, H.M. (2012) Mechanistic Models for the Intramolecular Hydroxycarbene-Formaldehyde Conversion and Their Intermolecular Interactions: Theory and Chemistry of Radicals, Mono-, and Dications of Hydroxycarbene and Related Configurations. International Journal of Quantum Chemistry, 112, 3711-3719.
https://doi.org/10.1002/qua.24127 - 14. Keeffe, J.R., Gronert, S., Colvin, M.E. and Tran, N.L. (2003) Identity Proton-Transfer Reactions from C-H, N-H, and O-H Acids. An ab Initio, DFT, and CPCM-B3LYP Aqueous Solvent Model Study. Journal of the American Chemical Society, 125, 11730-11745.
https://doi.org/10.1021/ja0356683 - 15. Gronert, S. and Keeffe, J.R. (2006) Primary Semiclassical Kinetic Hydrogen Isotope Effects in Identity Carbon-to-Carbon Proton- and Hydride-Transfer Reactions, an ab Initio and DFT Computational Study. The Journal of Organic Chemistry, 71, 5959-5968.
https://doi.org/10.1021/jo0606296 - 16. Gunbas, G. and Mascal, M.J. (2013) Extraordinary Modes of Bonding Enabled by the Triquinane Framework. The Journal of Organic Chemistry, 78, 9579-9583.
https://doi.org/10.1021/jo401715s - 17. Katrusiak, A. and Szafránski, M. (2006) Disproportionation of Pyrazine in NH+ N Hydrogen-Bonded Complexes: New Materials of Exceptional Dielectric Response. Journal of the American Chemical Society, 128, 15775-15785.
https://doi.org/10.1021/ja0650192 - 18. Yamashita, M., Yamamoto, Y., Akiba, K., Hashizume, D., Iwasaki, F., Takagi, N. and Nagase, S. (2005) Syntheses and Structures of Hypervalent Pentacoordinate Carbon and Boron Compounds Bearing an Anthracene Skeleton-Elucidation of Hypervalent Interaction Based on X-Ray Analysis and DFT Calculation. Journal of the American Chemical Society, 127, 4354-4371.
https://doi.org/10.1021/ja0438011 - 19. Buck, H.M. (2010) A Linear Three-Center Four Electron Bonding Identity Nucleophilic Substitution at Carbon, Boron, and Phosphorus. A Theoretical Study in Combination with Van’t Hoff Modeling. International Journal of Quantum Chemistry, 110, 1412-1424.
http://dx.doi.org/10.1002/qua.22252 - 20. Hamerlinck, J.H.H., Schipper, P. and Buck, H.M. (1980) 3,3,3’,3’-Tetramethyl-1,1’-Spirobi[3H-2,1-Benzoxaphosph(v)ole]-1-yl Radical: Evidence of a Correlation between Pseudorotation and Stereoisomerisation. Journal of the Chemical Society, Chemical Communications, 975-977.
https://doi.org/10.1039/C39800000975 - 21. Imoto, S., Kibies, P., Rosin, C., Winter, R., Kast, S.M. and Marx, D. (2016) Toward Extreme Biophysics: Deciphering the Infrared Response of Biomolecular Solutions at High Pressures. Angewandte Chemie International Edition, 55, 9534-9538.
https://doi.org/10.1002/anie.201602757 - 22. Stefl, S., Nishi, H., Petukh, M., Panchenko, A.R. and Alexov, E. (2013) Molecular Mechanisms of Disease-Causing Missense Mutations. Journal of Molecular Biology, 425, 3919-3936.
https://doi.org/10.1016/j.jmb.2013.07.014 - 23. Sadilèk, M. and Turecek, F. (1996) Experimental Evidence for Metastable Hydrosulfonium Radical H3S. Journal of Physical Chemistry, 100, 15027-15032.
https://doi.org/10.1021/jp9608640 - 24. (a) Janssen, R.A.J., Sonnemans, M.H.W. and Buck, H.M. (1986) Electron Capture Phosphoranyl Radicals in X-Irradiated Diphosphine Disulfides. A Single Crystal ESR and ab Initio Quantum Chemical Study. Journal of Physical Chemistry, 84, 3694-3708.
https://doi.org/10.1063/1.450209
(b) Janssen, R.A.J., Kingma, J.A.J. and Buck, H.M. (1988) A Single-Crystal ESR and Quantum Chemical Study of Electron-Capture Trialkylphosphine Sulfide and Selenide Radical Anions with a Three-Electron Bond. Journal of the American Chemical Society, 110, 3018-3026.
https://doi.org/10.1021/ja00218a004
(c) Janssen, R.A.J., van der Woerd, M.J., Aagaard, O.M. and Buck, H.M. (1988) A Single-Crystal ESR Study on Radicals Derived from Rac- and Meso-1,2-Dime-thyl-1,2-Diphenyldiphosphine Disulfide: Stereochemical Selection in Radical Formation. Journal of the American Chemical Society, 110, 6001-6006.
https://doi.org/10.1021/ja00226a013 - 25. (a) Aagaard, O.M., Janssen, R.A.J., de Waal, B.F.M., Kanters, J.A., Schouten, A. and Buck, H.M. (1990) Intermolecular Effects on the Radiogenic Formation of Electron-Capture Phosphorus-Centered Radicals. A Single-Crystal ESR Study of Diastereoisomeric Precursors. Journal of the American Chemical Society, 112, 938-944.
https://doi.org/10.1021/ja00159a005
(b) Aagaard, O.M., Janssen, R.A.J., de Waal, B.F.M. and Buck, H.M. (1991) Reactivity in Molecular Crystals: Radical Formation in Chiral Phosphorus Compounds. Heteroatom Chemistry, 2, 39-43.
https://doi.org/10.1002/hc.520020106 - 26. Steudel, R. (2003) Elemental Sulfur and Sulfur-Rich Compounds I. Springer, Berlin.
https://doi.org/10.1007/b12115 - 27. Eustis, S.N., Radisic, D., Bowen, K.H., Bachorz, R.A., Haranczyk, M., Schenter, G. and Gutowski, M. (2008) Electron-Driven Acid-Base Chemistry: Proton Transfer from Hydrogen Chloride to Ammonia. Science, 319, 936-939.
https://doi.org/10.1126/science.1151614 - 28. Miyata, Y., Nakayama, K., Sugawara, K., Sato, T. and Takahashi, T. (2015) High-Temperature Superconductivity in Potassium-Coated Multilayer FeSe Thin Films. Natural Materials, 14, 775-779.
https://doi.org/10.1038/nmat4302 - 29. Carlsson, A.-C.C., Grafenstein, J., Budnjo, A., Laurila, J.L., Bergquist, J., Karim, A., Kleinmaier, R., Brath, U. and Erdélyi, M. (2012) Symmetric Halogen Bonding Is Preferred in Solution. Journal of the American Chemical Society, 134, 5706-5715.
https://doi.org/10.1021/ja301341h - 30. Karim, A., Reitti, M., Carlsson, A.-C.C., Grafenstein, J. and Erdélyi, M. (2014) The Nature of [N-Cl-N]+ and [N-F-N]+Halogen Bonds in Solution. Chemical Science, 5, 3226-3233.
https://doi.org/10.1039/c4sc01175a - 31. Bedin, M., Karim, A., Reitt, M., Carlsson, A.-C.C., Topic, F., Cetina, M., Pan, F., Havel, V., Al-Ameri, F., Sindelar, V., Rissanen, K., Grafenstein, J. and Erdélyi, M. (2015) Counterion Influence on the N-I-N Halogen Bond. Chemical Science, 6, 3746-3756.
https://doi.org/10.1039/C5SC01053E - 32. Thanthiriwatte, K.S., Sptuell, J.M. and Dixon, D.A. (2014) Structures, Vibrational Frequencies, and Stabilities of Halogen Cluster Anions and Cations, Xn+/–, n = 3, 4, and 5. Inorganic Chemistry, 53, 8136-8146.
https://doi.org/10.1021/ic501211f - 33. Zhang, W., Oganov, A.R., Goncharov, A.F., Zhu, Q., Boulfelfel, S.E., Lyakhov, A.O., Stavrou, E., Somayazulu, M., Prakapenka, V.B. and Konopková, Z. (2013) Unexpected Stable Stoichiometries of Sodium Chlorides. Science, 342, 1502-1505.
https://doi.org/10.1126/science.1244989 - 34. Zhang, J., Kuo, J.L. and Iitaka, T. (2012) First Principles Molecular Dynamics Study of Filled Ice Hydrogen Hydrate. The Journal of Chemical Physics, 137, Article ID: 084505.
https://doi.org/10.1063/1.4746776







