Open Journal of Physical Chemistry
Vol. 2 No. 1 (2012) , Article ID: 17527 , 8 pages DOI:10.4236/ojpc.2012.21002
Quasicrystals
Department of Physics, Bu-Ali Sina University, Hamedan, Iran
Email: *fsamavat@yahoo.com
Received June 15, 2011; revised November 23, 2011; accepted December 24, 2011
Keywords: Quasicrstals; Icosahedral Quasicrystals; Polygonal Quasicrystals; Aperiodic Intermetallics
ABSTRACT
Quasicrystals are material with perfect long-range order, but with no three-dimensional translation periodicity. They are typically binary and ternary metallic alloys. Quasicrystals have characteristic physical properties. Some resemble those of periodic crystals while others have similar properties to amorphous alloys. Many of their mechanical physical properties are quite unusual by the standards of common metals. The peculiar physical properties of quasicrystals certainly give rise to the hope that they may become of some practical importance in the future. Some of these properties are surface related. This provides the main motivation for surface scientists to study this material. In this paper; quasicrystals, types of them, physical properties, surface science and potential applications of them have been discussed.
1. Introduction
A crystal is defined as a three dimensional periodic arrangement of atoms or molecules with transitional periodicity along its three principal axes [1]. Thus it is possible to obtain an infinitely extended crystal structure by aligning building blocks called unit-cells until the space is filled up. In 1984, Dan Shechtman, Blech, Gratias & Cahn discovered quasi-crystals (QCs) [2,3] which are well ordered but aperiodic intermetallics. These are typically binary and ternary metallic alloys often containing 60% - 70% aluminium which exhibit unusual physical properties, such as low friction, low adhesion, high hardness and high wear resistance [4,5].
QCs also present unique structural features. To a surface scientist, quasicrystals are quite unusual because of several factors, the first of which is their structure. They are neither periodically ordered, like crystals, nor disordered or amorphous solids. They have a well defined, discrete group symmetry, like crystals [6], but one that is explicitly incompatible with three-dimensional periodic translation order (e.g. exhibiting 5, 8, 10, or 12-fold symmetry axes). Crystal lattices can be carried or mapped into themselves by various symmetry operations. A typical symmetry operation is that of rotation about an axis that passes through a lattice point. Lattices can be found such that 1, 2, 3, 4, and 6-fold rotation axes carry the lattice into itself. But, we can not find a lattice that goes into itself under 2π/5 radians. Therefore we should not expect the lattice to have 5-fold rotation axis because it is not possible to fill all space with a connected array of pentagons. However, quasicrystals do exhibit 5-fold symmetry.
The other element of strangeness about quasicrystals is that many of their mechanical-physical properties are quite unusual by the standards of common metals. Some of these properties are surface related. This intriguing element provides the main motivation for surface scientists to study these materials.
2. The Concept of Higher Dimensional Space
Quasicrystals are materials with perfect long-range order, but with no three-dimensional translational periodicity. Since quasicrystals lose periodicity in at least one dimension it is not possible to describe them in 3D-space as easily as normal crystal structures. Thus it becomes more difficult to find mathematical formalisms for the interpretation and analysis of diffraction data. For normal crystals we can assign three integer values (Miller indices) to label the observable reflections [1]. This is due to the three-dimensional translational periodicity of the structure. Quasicrystals are periodic if one goes to six (or higher) dimensional space [7]. In order to assign integer indices to the diffraction intensities of quasicrystals, however, at least 5 linearly independent vectors are necessary. So we need 5 indices for polygonal quasicrystals and 6 indices for icosahedral quasicrystals. Atomic order is best defined in terms of the Fourier transform of the mass density of the solid. In an ordinary crystal, this transform can be written as a Fourier series [1]:
 (1)
(1)
The set of wavevectors G define a discrete reciprocal lattice in which each wavevector in the sum can be written as an integer linear combination of three “basis” vectors ai*
 (2)
(2)
The ai* are linearly independent integer, which means that G = 0 if and only if all the h, k, l = 0. The ai* are said to span the reciprocal lattice. They are related to the “basis” vectors ai that define the unit cell if crystal in physics space [1]:
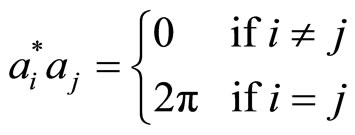
In a quasi-crystal, the Fourier transform of the mass density is also a Fourier series and the wavevectors in the Fourier sum also form a discrete reciprocal lattice. However, the number of integer linearly independent basis vectors required to “span” the reciprocal lattice exceeds the spatial dimension, and the point symmetry of the reciprocal lattice is incompatible with periodic translational order. For example, six basis vectors are required to span the reciprocal lattice for three-dimensional quasi-crystals with icosahedral symmetry:
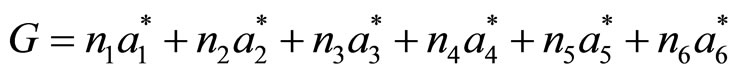 (3)
(3)
where the ai* can be selected to point along the fivefold axes of an icosahedron. They are called generalized Miller indices. The necessary n vectors span an nD-reciprocal space. Therefore there is also a nD-direct space in which a structure can be built that gives rise to a diffraction pattern as it is observed for quasicrystals. To put it simply it can be said that in the higher-dimensional space a quasi periodic structure can be described as a periodic one. Thus it is enough to define a single unit cell of the nD-structure. This enables us to describe the whole quasicrystal structure with a finite set of parameters. If we described it in 3D-space only, we needed thousands of atoms to obtain a representative volume segment of the whole structure.
3. Experimental Discovered
Quasicrystals were discovered in 1982, when Dan Shechtmen observed patterns of sharp spots with icosahedral symmetry in selected area electron diffraction patterns of a rapidly cooled Al-Mn alloy [2]. It took about two years before an account of this icosahedral phase appeared in print.
Independently, another type of quasicrystal with a twelevefold rotational axis was found in a Ni-Cr alloy [8]. This dodecagonal phase was also characterized by sharp electron diffraction spots, a clear evidence of an ordered structure. Subsequently, two more types of quasicrystals with ten-and eightfold rotational symmetry were found. Again by selected area election diffraction, a decagonal phase was observed in a rapidly solidified Al-Mn alloy [9] with a somewhat higher Mn content than those used by Shechtman et al. [2]. An octagonal phase was first found in rapidly solidified V-Ni-Si and Cr-Ni-Si alloy [10].
Thus, the peculiar property of quasicrystals that led to their experimental discovery is the occurrence of sharp spots in electron diffraction patterns with symmetries that are not found in “conventional” crystals. In other words, quasicrystals are well-ordered solids with unusual symmetry properties.
4. Non-Crystallographic Symmetry
The crystallographic restriction or crystallographic lemma states that, in two and three dimensions, a lattice can only have rotational symmetry axes of order one, two, three, four or six, corresponding to angles of 360˚, 180˚, 120˚, 90˚ and 60˚, respectively and integer multiphase of these elementary rotation angles. The proof of this lemma is elementary. If a rotation is a symmetry of the lattice; it has to map the vectors that span the lattice onto integer linear combinations of themselves. This immediately restricts the set of possible angles P to those where 2Cos (P) is integer, which gives precisely the list above with their multiples. Clearly, there is no three-dimensional lattice showing icosahedral symmetry, and none with a symmetry axis of order fire, eight, ten, or twelve. Nevertheless, the sharpness of the observed diffraction spots shows that the atomic positions in these solids must be long-range ordered; quasicrystals are clearly distinct from amorphous solids. The only solution that remains is to give up the idea that the atoms are arranged according to a periodic lattice, that is, the arrangement of atoms in a quasicrystals is ordered, but aperiodic. For the icosahedral phase, this is true in all directions of space; there is no periodicity whatsoever.
5. Types of Quasicrystals
The icosahedral quasicrystals form one group and the polygonal quasicrystals another (8, 10, 12-fold symmetry). The former is manifested in the occurrence of sharp diffraction spots and the latter in the presence of a non-crystallographic rotational symmetry. The polygonal or dihedral quasicrystals are periodic in one direction, so they consist of a periodic sequence of slices with twelve-, ten-, or eightfold symmetry. They are quasi periodic in two dimensions. There is one periodic direction perpendicular to the quasi-periodic layers. For the icosahedral phase, this is true in all directions of space; there is no periodicity whatsoever. They are quasiperiodic in three dimensions. There is no periodic direction. The symmetry that determines the type of the quasicrystals is first seen in its diffraction pattern. Simulations of some diffraction patterns are shown in Figure 1. These could represent either electron diffraction patterns or the Zeroth layers of precession photographs (X-ray). A simulation for a Laue pattern (X-ray) from an icosahedral quasicrystal is shown in Figure 2, where the X-ray beam is along one of the five-fold axes.
6. Systems with Quasicrystals
The first quasicrystalline samples were found in rapidly solidified binary alloys, an icosahedral and a decagonal phase in Al-Mn and the dodecagonal phase in Ni-Cr. These phases are metastable, as is the case for a sizable fraction of the known quasicrystals. The first thermodynamically stable icosahedra quasicrysrtals were found in a ternary Al-Cu-Li alloy, and today quite a collection of stable icosahedral and a decagonal phase is known.
Typically, stable quasicrystals occur in ternary or quaternary alloys. A large class consists of Al-based alloys, the most prominent being Al-Cu-Fe, Al-Pd-Mn, and Al-Pd-Re, which shows highly, ordered icosahedral phases. There is also a stable decagonal phase in the Al-Pd-Mn system.
Although Al-based quasicrystals play a major role, it is by no means true that these exhaust all quasicrystalline materials. A new class of stable icosahedral quasicrystals was discovered in Mg-Zn alloys containing rare earth elements. These are very interesting from the physical point of view because the rare earth elements, due to their large magnetic moments, are expected to lead to interesting magnetic properties of these materials. Other materials that may be important for applications are Ti-Zr-based quasicrystals.


Figure 1. Simulations of some diffraction patterns.
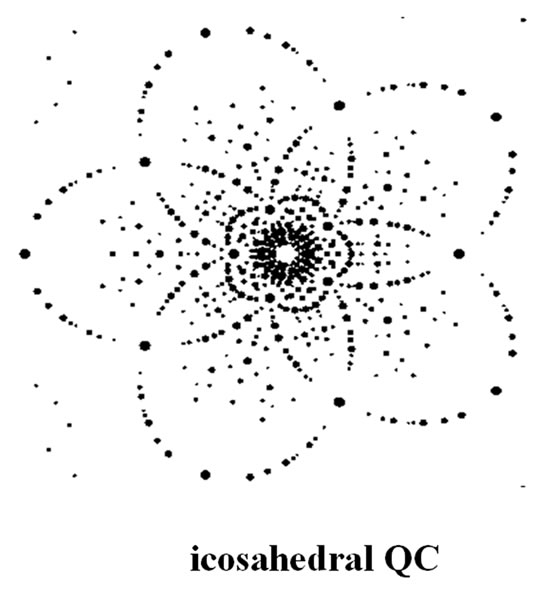
Figure 2. A simulation from an icosahedral quasicrystal.
7. Physical Properties
Quasicrystals have characteristic physical properties. Some resemble those of periodic crystals while others have similar properties to amorphous alloys. Many of their mechanical physical properties are quite unusual by the standards of common metals. Some of these properties are surface related. This provides the main motivetion for surface scientists to study this material. Some of the physical properties of quasicrystals, relative to selected benchmark materials, are shown in Table 1. Two ternary quasicrystal line materials were chosen for Table 1. They are icosahedral (i-)-Al-Pd-Mn and i-Al-Cu-Fe.
The latter alloy is of some commercial interest because it is an equilibrium phase with inexpensive components. The values of Vickers’ hardness, Hv [11,12] in Table 1 demonstrate that this quasicrystal is harder than any of its individual components and comparable in hardness to silica. Quasicrystals also exhibit a low coefficient of friction and is reputed to be relatively unreactive (i.e. nonstick) [28,29]. The combined properties of high hardness, low friction and inertness lead naturally to speculation that quasicrystals maybe useful as low-friction or release coating in industrial settings where abrasion resistance is also important. However, to date, such an application has not reached the marketplace.
The results in Table 1 also illustrate other properties, including brittleness, elasticity, conductivity, and surface energy. Quasicrystals are quite brittle, illustrated by the low value of fracture toughness, which is a drawback for many applications [12,15]. Its elasticity, judged by its Young’s modulus, is comparable to that of typical metals [12,16]. Although metallic, quasicrystals are poor thermal and electrical conductors, which can be put to good use in thermal barrier applications. Quasicrystals exhibit a rather low surface energy which is much lower than of a typical clean metal and significantly lower than that of an oxidized metal (alumna) [14,19]. Finally, although not shown in Table 1, qualitative observations suggest that the quasicrystals are resistant to oxidation. For the first studies of surface oxidation [20,21] i-Al-Pd-Mn were chosen because, starting in the early 1990s, it could be grown in large, single-grain form [22,23]. Later studies have indicated, however, that oxidation phenomena on i-Al-Pd-Mn and i-Al-Cu-Fe are quite similar [24]. Hence, the i-Al-Pd-Mn, although not commercially attractive because of its precious metal content, may serve as a useful model for understanding oxidation of the other Al-rich quascrystalline alloys.
8. Surface Science of Quasicrystals
Early interest in surfaces of quasicrystals was sparked by the observation of the beautifully facetted growth structures. At that time, a variety of shapes had been observed. The current generation of work on surfaces of quasicrystals was ushered in by the use of ultrahigh vacuum (UHV), and associated spectroscopies and microscopies, to examine these materials. A group of experimentalists at AT & T Bell laboratories were the pioneers, performing

Table 1. Physical properties of icosahedral alloys, compared with relevant benchmark materials at room temperature.
the first LEED and STM experiments on surfaces of decagonal AL-Co-Cu [25]. Subsequent work focused mainly upon icosahedral Al-Pd-Mn, primarily because of availability of good samples, and icosahedral Al-Cu-Fe. Thus, all work to date concerns Al-rich alloys. The research is driven by the fact that several attractive properties of quasicrystals (low friction, good oxidation resistance, low surface energy) involve surface phenomena. A main goal is to determine whether and how these properties may be related to the unusual atomic structure. Furthermore, in most proposed applications, quasicrystals would be in the form of low-dimensional solids-coatings, thin films, precipitates, or composites-where the ratio of surface area to volume is high, and where surface or interface properties could be crucial to the success of the application [5,14]. This section first discusses the preparation of clean surfaces, then the chemical composition of surfaces, their structure and their surface chemistry.
8.1. Preparation of Clean Surfaces
Typically, a clean surface can only be prepared and preserved for a reasonable length of time within an Ultrahigh Vacuum (UHV) environment. Quasicrystals can undergo surface oxidation and contamination, so that a sample prepared in air by any means contains the same contaminants observed on crystalline metals-oxide(s), as well as carbonand sulfur-containing compounds. Furthermore, heating a sample can cause surface segregation of trace impurities from the bulk. One of the approaches for cleaning the sample is, transferring the sample to UHV and bombarded with noble gas ions (sputtered) to remove surface material, then annealing to remove the structural and chemical damage left by sputtering. This can be done repeatedly until segregation of bulk contaminants is eliminated.
8.2. Surface Composition
Many studies of surface composition have been reported, using X-ray Photoelectron Spectroscopy (XPS) and Auger Electron Spectroscopy (AES), techniques which provide a depth-weighed average over approximately the top 10 nm of material. All such studies have been on sputter-annealed surfaces, one is represented in Figure 3, demonstrating the AES-based compositions as a function of temperature after Ar sputtering of the fivefold surface of i-Al-Pd-Mn [33].
8.3. Surface Structure
In studies of the surface structure of quasicrystals, the type of information obtained depends sensitively upon surface preparation and surface composition. Sputtering usually leaves a non-stoichiometric surface which can return to equilibrium by annealing to very high temperatures.
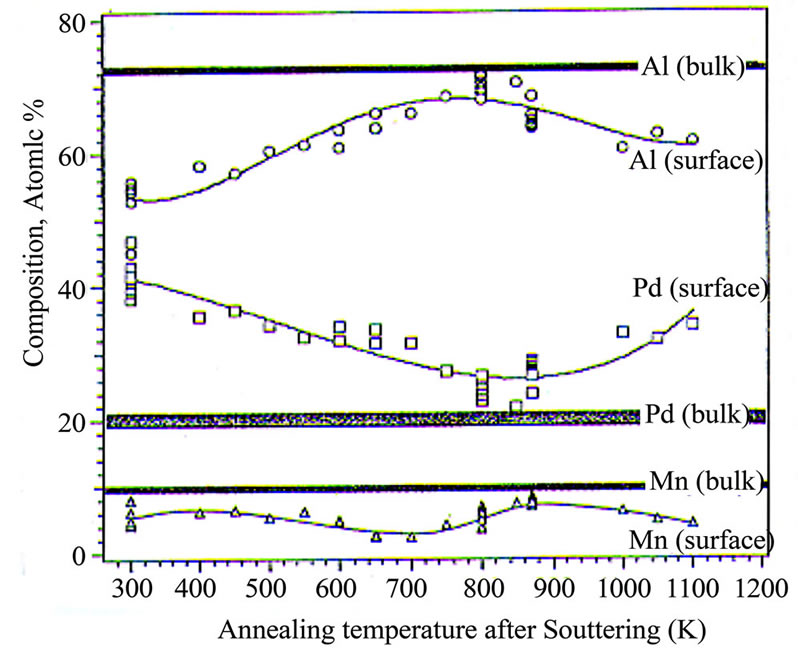
Figure 3. Surface atomic compositions, based upon Auger Electron Spectroscopy, as a function of annealing temperature in UHV [33].
8.4. Surface Chemistry
Another fundamental surface property is chemical reactivity. Studies under various environmental conditions suggest that quasicrystals are relatively unreactive and/or surface energy is very low, suggesting a non-stick character which maybe useful as a coating. The surface energy of a clean metal is typically in the range of a few thousand mJ/m2, of aluminum oxide about 50 mJ/m2 and of polytetrafluoro ethylene (PTFE) about 17 - 18 mJ/m. Air-oxidized i-Al-Cu-Fe has a surface energy close to that of PTFE, about 24 - 25 mJ/m2, and significantly lower than that of alumina [14,16]. It has been proposed that the surface chemistry of quasicrystals should be dominated by the suppression of the density of states at the fermi level [27]. This hypothesis is supported by measurements which reveal that, under atmospheric condition, the surface of quasicrystal behaves more like a covalently bonded material (e.g. Teflon) than like a metal; the polar component of the surface energy is much lower even than that of crystalline phases which are similar in composition and local structure [28]. A low polar component suggests low surface polarizability, i.e. low freeelectron density.
9. Potential Applications
Perhaps the fastest growing sub field of quasicrystal research in the 1990s has been the area of technological applications based upon the interesting combinations of physical properties that many of these systems offer. The desirable mechanical properties of quasicrystalline alloys, discussed in the previous section, include low surface energies and coefficients of friction, good oxidation and corrosion resistance, and high hardness. Furthermore, at least in the case of Al-Cu-Fe, the constituent elements are readily available, low-cost, and non-toxic. Together with their low thermal and electrical conductivity and some unusual optical behavior, the mechanical properties listed above show great potential for application in the realm of coatings.
Nowadays, the question of potential industrial applications of non-materials plays a major role. The peculiar physical properties of quasicrystals certainly give rise to the hope that they may become of some practical important in the future. The three main applications are outlined below.
9.1. Surface Coatings
The most important area of applications concerns the use of quasicrystals as materials for surface coatings. This is favoured against the use of bulk material because bulk quasicrystals tend to be rather brittle, while coatings benefit from the hardness of qusicrystals. The most prominent example is the application of quasicrystalline coatings to frying pans—an application that has been famous in the quasicrystal community for years though it has not been realised until just recently that a quasicrystal-coated frying pan appeared on the market. They are now sold by the French Company Sitram under the trademark cybernox [29].
9.2. Alloys Containing Quasicrystalline Nanoparticles
A different way to circumvent the brittleness of quasicrystalline bulk material while preserving some of its useful properties is the utilization of an Al-based alloy (typically Al-Mn-Ce) reinforced by precipitation of icosahedral particles in the nanometer range. Such materials, which are now commercially available in Japan, are of great technological interest because they can be very strong but much lighter than other material with comparable physical properties. Examples of applications that have already been realized are razor blades and surgeon’s instruments, though this may have been more by chance than being an intentional application of quasicrystals. Nevertheless they will undoubtedly find their way to applications in many different areas such as the aviation industry [30].
9.3. Hydrogen Storage
A third, and maybe more speculative, application concerns the use of quasicrystals as a reversible storage medium for hydrogen. The most promising quasicrystal materials for hydrogen storage are Zr-based quasicrystals [31]. For such systems, storage capabilities of almost two hydrogen per metal atom have been reported, comparable to the storage capability of the Ti-Fe hybrids, which have already been applied in non-polluting internal combustion engines.
A less desirable feature of QCs, however, is that at temperatures lower than about 70% - 80% of the melting temperature, these alloys are very brittle, limiting the range of applications of bulk material. The hardness of icosahedral Al-Pd-Mn at room temperature, for example, exceeds that of most steels, but it has very low fracture toughness.
One way to avoid the difficulties inherent to the extreme brittleness of bulk quasicrystalline alloys is to deposit them as coating on more robust substrates. In this manner, the desirable properties can be exploited while maintaining the mechanical integrity of the substrate. Most of the interest in applications so far has focused on the use of thick or thin coatings of quasicrystals. Applications can make use of the high strengh of these alloys as wear resistant coatings for steel and aluminium parts in manufacturing and the automotive industries.
Moving beyond the chemical properties of quasicrystal surface, there are other physical properties such as low thermal conductivity and low diffusivity [32], which show promise for applications as thermal barrier coatings.
10. Diffusion in Quasicrystals
Diffusion properties are important for the production of quasicrystals and for application of these materials at elevated temperatures. Diffusion in solid materials, irespective of whether they are crystalline or quasicrystalline, is an important topic of materials science. Diffusion processes play a key role in the production and heat treatments of materials and in the kinetics of many microstructural changes and their associated properties. The atomic mechanisms of diffusion in crystalline materials are closely linked to defects. Point defects such as vacancies and self-interstitials are the simplest defects. A new kind of defect called a phason exists in quasiperiodic structures. Phasons are violations of the matching rules of a quasiperiodic structure. Kalugin and Katz have proposed a self-diffusion mechanism via phason flips without the presence of vacancies [34]. It has been suggested that the diffusion rate via the phason mechanism can be much faster than conventional diffusion processes.
11. Summary
A Quasicrystal is a material which shows diffraction patterns with rotational symmetries that are a “forbidden” by classical crystallography. The structure of quasicrystals is comprised of atoms that are arranged in nonoperiodic fashion. Quasicrystal structures show long-range order, but no translational periodicity. Quasicrystals are typically binary and ternary metallic alloys, often containing 60% - 70% aluminium. They present unique structural features, coupled with unusual combinations of physical properties. Some of the interesting properties of quasicrystals, such as low friction and “non-stick” character, involve surface phenomena. Studies have shown that quasicrystalline materials exhibit low coefficients of friction, are wear resistant, and are hard. In most proposed applications, QCs would be in the form of lowdimensional solids-coatings, thin films, precipitates, or composites where the areas in quasicrystal research that have seen great advances in the past 10 years, each of these topics represent new horizons.
REFERENCES
- C. Kittel, “Introduction to Solid State Physics,” John Wiley, New York, 1983.
- D. Shechtman, I. Blech and D. Gratias, “Metallic Phase with Long-Range Orientational Order and No Translational Symmetry,” Physical Review Letters, Vol. 53b, No. 20, 1984, pp. 1951-1953.
- A. I. Goldman and M. Widom, “Quasicrystal Structure and Properties, “Annual Reviews of Physical Chemistry, Vol. 92, 1991, pp. 685-729. doi:10.1146/annurev.pc.42.100191.003345
- S. S. Kang, J. M. Dubois and J. Von Stebut, “Tribological Properties of Quasicrystalline Coatings,” Journal of Materials Research, Vol. 8, No. 10, 1993, pp. 2471-2481. doi:10.1557/JMR.1993.2471
- J. M. Dubois, S. S. Kaing and A. Perrot, Materials Science and Engineering, Vol. A179/A180, 1994, pp. 122-126.
- A. I. Goldman and M. Widom, “Quasicrystal Structure Abd Properties,” Annual Review of Physical Chemistry, Vol. 42, 1991, pp. 685-729. doi:10.1146/annurev.pc.42.100191.003345
- http://mcs.open.ac.uk/ugg2/quasi_intro2.html-ssi
- T. Ishimasa, H. Nissen and Y. Fukano, “New Ordered State between Crystalline and Amorphous in Ni-Cr Particles,” Physical Review Letters, Vol. 55, No. 5, 1985, pp. 511-513. doi:10.1103/PhysRevLett.55.511
- L. Bendersky, “Quasicrystal with One-Dimensional Translational Symmetry and a Tenfold Rotation Axis,” Physical Review Letters, Vol. 55, No. 14, 1985, pp. 1461-1463. doi:10.1103/PhysRevLett.55.1461
- N. Wang, H. Chen and K. H. Kuo, “Two-Dimensional Quasicrystal with Eightfold Rotational Symmetry,” Physical Review Letters, Vol. 59, No. 9, 1987, pp. 1010-1013. doi:10.1103/PhysRevLett.59.1010
- U. Koster, W. Liu, H. Liebertz and M. Michel, “Mechanical Properties of Quasicrystalline and Crystalline Phases in Al3Cu2Fe Alloys,” Journal of Non-Crystalline Solids, Vol. 153-154, 1993, pp. 446-452. doi:10.1016/0022-3093(93)90393-C
- Y. Yokoyama, A. Inoue and T. Masumoto, Materials Transactions, Vol. 34, 1993, pp. 135-145.
- S. S. Kang, J. M. Dubois and J. Von Stebut, “Tribological Properties of Quasicrystalline Coatings,” Materials Research, Vol. 8, No. 10, 1993, pp. 2471-2481. doi:10.1557/JMR.1993.2471
- J. M. Dubois, In: A. I. Goldman, D. J. Sordelet and P. A. Thiel, Eds., Proceedings of the Conference New Horizons in Quasicrystals, World Scientific, Singapore City, Vol. 77, 1997, pp. 1928-1938.
- D. Kovar and M. J. Ready, “Role of Grain Size in Strength Variability of Alumina,” American Ceramic Society, Vol. 77, No. 7, 1994, pp. 1928-1938. doi:10.1111/j.1151-2916.1994.tb07073.x
- H. E. Boyer, T. L. Gall, “Metals Handbook,” Desk Edition, American Society for Metals, Metals Park, 1984.
- I. M. Hutchings, “Tribology: Frictions and Wear Engineering Materials,” CRC, Boca Raton, 1992.
- J. M. Dubois and P. Weinland, “CNRS, Nancy, France, Coating Materials for Metal Alloys and Metals and Method,” Eur. Patent Ep 0356287 Al and U.S. Patent 5, Vol. 204, 1993, p. 191.
- F. R. de Boer, R. Boom, W. C. M Mattens, A. R. Meidema and A. K. Niessen, “Cohesion in Metals,” NorthHolland, Amsterdam, 1988.
- S. L. Chang, W. B. Chin, C. M. Zhang, C. J. Jenks and P. A. Thiel, “Oxygen Adsorption on a Single-Grain, Quasicrystal Surface,” Surface Science, Vol. 337, No. 1-2, 1995, pp. 135-146. doi:10.1016/0039-6028(95)00564-1
- S. L. Chang, C. M. Zhang, C. J. Jenks, J. W. Andereg and P. A. Thiel, In: C. Janot and R. Mosseri, Eds., Procceding of the 5th International Conference on Quasicrystals, World Scientific, Singapore City, 1995, pp. 786-789.
- Y. Yokoyama, A. P. Tsai, A. Inoue and T. Masumoto, Materials Transactions, Vol. 32, 1991, pp. 1089-1097.
- Y. Yokoyama, T. Miura, A. P. Tsai, A. Inoue, T. Masumotos, Materials Transactions, Vol. 33, 1992, pp. 97-101.
- C. J. Jenks, P. J. Pinhero, S. L. Chang, J. W. Anderegy, M. F. Besser, D. J. Sordelet and P. A. Thiel, In: A. I. Goldman, D. J. Sordelet, P. A. Thiel and J. M. Dubois, Eds., Proceedings of the Conference New Horizons in Quasicrystals, World Scientific, Singapore City, 1997, pp. 157-164.
- A. R. Kortan, R. S. Becker, P. A. Thiel and H. S. Chen, “Real-Space Atomic Structure of a Two-Dimensional Decagonal Quasicrystal,” Physical Review Letters, Vol. 64, No. 2, 1990, pp. 200-203. doi:10.1103/PhysRevLett.64.200
- F. R. Deboer, R. Boom, W. C. M. Mattens, A. R. Meidema and A. K. Niessen, “Cohesion in Metals,” NorthHolland, Amsterdam, 1988.
- N. Rivier, Proceeding of the Conference, New Horizons in Quasicrystals, Research and Applications, World Scientific, Singapore City, 1997, p. 188.
- J. M. Dubois, P. Plaindoux, E. Belin-Ferre, N. Tamure and D. J. Sordelet, Proceeding of the 6th International Conference on Quasicrystals, World Scientific, Singapore City, 1998, p. 733.
- http://www.inductionsystems.com/cookware/cybernox.htm.
- S. Takeuchi and T. Fujiwara (Eds.), Proceedings of the 6th International Conference on Quasicrystals, World Scientific, Singapore City, 1998.
- G. Coddens, A. M. Viano, P. C. Gibbons, K. F. Kelton and M. J. Kramer, “Time-of-Flight Neutron Scattering Study of Hydrogen Dynamics in Icosahedral Ti45Zr38 Ni17H150 Quasicrystals,” Solid State Communications, Vol. 104, 1997, pp. 179-182. doi:10.1016/S0038-1098(97)00110-5
- P. Archamboult and C. Janot, MRS Bulletin, Vol. 22, 1997, p. 48.
- A. I. Goldman and P. A. Thiel, Horizons in Quasicrysral Research, 1999, pp. 561-601.
- P. A. Kalugin and A. Katz, “A Mechanism for Self-Diffusion in Quasi-Crystals,” Europhysics Letters, Vol. 21, No. 9, 1993, p. 921. doi:10.1209/0295-5075/21/9/008
NOTES
*Corresponding author.

